變厚度復合材料板低速沖擊能量監測

陸 觀，梁大開，徐一鳴，邱自學

(1.南通大學 機械工程學院，江蘇 南通 226019；2.南京航空航天大學 機械結構力學與控制國家重點實驗室，南京 210016；3.南通大學 電氣工程學院，江蘇 南通 226019)

復合材料在航空、機械、醫學等領域的應用日趨廣泛。隨之而來的問題就是復合材料在使用過程中的動態監測需求[1-3]。變厚度復合材料層合板的強度比一般復合材料板有所提高，但是動態載荷下的信號分析更為復雜。由于復合材料常常以層合板形式使用，因此結構受到的各種載荷可能會造成層合板的內部剝離、斷裂、脫層等等，尤其是低速沖擊所造成的內部損傷從外部不易察覺。傳統的復合材料結構日常檢測和維護雖然可以排除安全隱患，但會耗費大量的時間和成本，而實時監測變厚度復合材料層合板沖擊信號可以對結構低速沖擊損傷進行預警[4]。近年來，各國學者對復合材料變厚度結構進行了一些研究。李戈嵐等[5]研究了復合材料變厚度加筋板后屈曲、承載能力以及耐久性/損傷容限一體化設計；馬靜敏等[6]通過有限元方法分析了復合材料的彈性耦合、鋪層角度、截面變化和旋轉速度對復合材料變截面薄壁梁的自由振動的影響。但因為復合材料變厚度層合板沖擊信號的混疊嚴重，其沖擊監測研究的公開報道較少。

目前可以用于監測復合材料層合板沖擊載荷的傳感器有很多，其中光纖布拉格光柵(Fiber Bragg Grating, FBG)傳感器以其質量輕、體積小、耐腐蝕、抗干擾、可分布式、絕緣好等優勢得到了廣泛應用[7-9]。路士增等[10]利用FBG傳感器，結合小波分解重構算法、頻譜分析和支持向量多分類機算法研究了碳纖維復合材料板損傷的模式識別算法。蘆吉云等[11]研究了基于小波包特征提取及支持向量機的光纖-碳纖維復合材料結構沖擊定位方法。但是目前的相關研究較少涉及到變厚度復合材料結構的沖擊能量監測。

本文將光纖光柵傳感技術[12-14]應用于變厚度復合材料層合板低速沖擊監測并建立了沖擊能量監測系統，利用白化經驗模態分解(Whitening Empirical Mode Decomposition, WEMD)關鍵算法提取出沖擊混疊信號的特征值，并以此識別出低速沖擊能量等級。實驗證明光纖傳感技術可應用于變厚度復合材料結構的沖擊監測，在保證沖擊定位預警有效性的同時，使監測系統具有抗干擾、分布式等優勢。

1 基于FBG傳感技術的沖擊能量識別算法

1.1 光纖布拉格光柵傳感

光纖布拉格光柵對滿足光柵反射條件的入射光產生一種窄帶反射。基本原理為λ=2nΛ，其中λ為反射峰波長、Λ為光柵周期、n為有效折射率[15]。由于光柵周期的伸縮及彈光效應，光柵在受作用應力時會有波長的改變。假設此時傳感器只受到拉伸應變ε，由光柵周期及基本原理公式有：

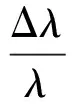
(1)

式中：Pe為有效彈光函數。由式(1)可知恒溫時光柵波長位移與縱向應變呈線性關系。沖擊載荷對結構的應力影響可以引起光纖光柵傳感器的中心波長偏移，因此可以將光纖光柵傳感器用于變厚度復合材料板沖擊研究。

1.2 沖擊特征提取算法

對光柵傳感器檢測到的沖擊信號進行特征提取，一般可用信號幅值、頻譜幅值、小波變換等方法。這里采用WEMD算法從復雜時間序列中直接分解出高頻至低頻的若干階獨立固有模態函數(Inirinsic Mode Function, IMF)分量，再進行頻譜分析得出沖擊特征值。由于變厚度復合材料的特性，使得經典EMD算法各階分解量雖然近似正交，但頻率混疊嚴重。因此這里提出了一種改進算法—WEMD，將分量矩陣進行白化，以降低混疊，且無需進行多次采樣。標準EMD算法的主要作用是去除信號疊加波且讓數據波形更對稱[16]。利用EMD算法，可將任意原始信號X(t)分解為：

(2)

Rx=Q∑2QT

(3)

式中：x為隨機信號、Q為累計量矩陣、∑-1QT為白化矩陣。由此得到各階分量ci(t)。

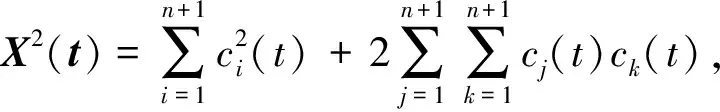
(4)

則任意兩分量ck、cj正交指數為：

(5)

各階分量正交，且因各分量為原始數據分解得，因此WEMD算法具有較好的自適應性。與標準算法不同的是，此改進算法無需進行多次采樣，對易受沖擊影響的工程試件有實用效果。

以上推導過程表明提出的WEMD算法，避免了固有模態信號模態混疊嚴重的問題，有效提高了信號處理率，提升了沖擊特征值有效性，增加了能量識別準確性。

1.3 沖擊能量識別步驟

在沖擊能量識別過程中，通過樣本信號的沖擊能量特征值來評估沖擊能量。首先，需要對所有沖擊樣本信號和待測信號進行WEMD分解；然后，計算樣本信號和待測信號的沖擊能量特征值，即傳感網絡的信號某階分量頻譜峰值，并建立沖擊樣本信號能量特征集合；最后，由于試件板的厚度較小區域對于沖擊能量較為敏感，因此根據傳感網絡信號第一階分量確定綜合厚度系數，用于修正能量特征集合，實現實際沖擊能量評估。綜上，針對變厚度復合材料層合板的沖擊能量識別算法具體步驟如下：

(l)在L個關鍵沖擊位置采集第1個沖擊能量下的信號數據，每個沖擊位置由N個傳感器采集到的沖擊響應信號向量組成了信號矩陣Xi=(xi1,xi2,…,xm,…,xiN)(其中i=1,2,3,…,L)，作為沖擊樣本信號。

(2)對信號向量xm進行WEMD分解，再求得各分量cj(t)與原始信號xm的相關系數。互相關系數為：

(3)選擇γ較大的分量ck(t)進行頻譜分析，得到頻譜峰值pm。同理可得信號矩陣Xi的頻譜峰值集合Pi=(pi1,pi2,…，pm,…，piN)(其中i=1,2,3,…,L)。

(4)將(2)中分解得到的c1(t)進行頻譜分析，得出峰值個數dm，其中界定峰值的閾值為M=pm/s,s為分量向量數目。同理可得信號矩陣Xi的峰值個數集合Di=(di1,di2,…,dm,…,diN)(其中i=1,2,3,…,L)。將Di歸一化后得到Xi的綜合厚度系數集合Hi=(hi1,hi2,…，hm,…，hiN)(其中i=1,2,3,…,L)。

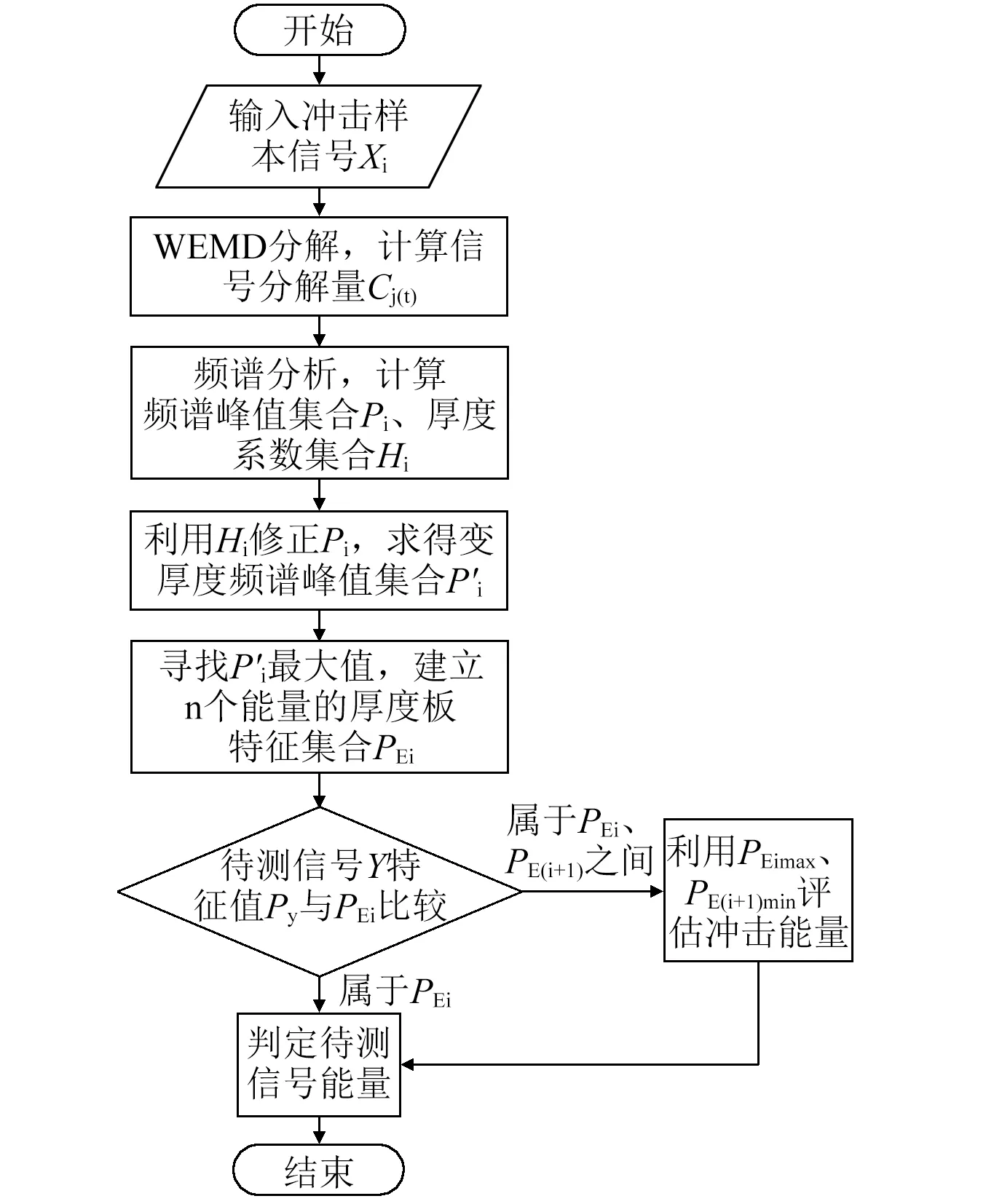
圖1 變厚度復合材料板沖擊能量識別流程圖Fig.1 Flow chart of low velocity impact energy identification for varied cross-section composite laminate

(7)同理，將采集的待測能量沖擊信號Y=(y1,y2,…,yN)進行WEMD分解，并求得特征值py。

(8)比較特征值py與變厚度板特征集合PEi范圍數值，評估沖擊能量等級。當驗證點的特征值屬于某級能量范圍內，或者大于最大級能量范圍，或者小于最小級能量范圍，則判定為該能量等級；若屬于兩級能量特征集合PEi和PE(i+1)之間，則根據py與PEimax、PE(i+1)min進行評估：

(7)

如圖1所示為變厚度復合材料層合板的沖擊能量識別流程圖。

2 沖擊實驗

2.1 變厚度復合材料層合板沖擊實驗裝置

如圖2所示，沖擊實驗系統由機翼油箱試件(表面為變厚度復合材料蒙皮)、沖擊錘、FBG傳感器、SI425型光纖光柵解調儀及計算機組成。其中SI425型光纖光柵解調儀的4個光學通道上可通過FC/PC接口連接多達512個FBG傳感器，用于靜態以及動態信號的測量；可檢測波長范圍為1 520 nm～1 570 nm，分辨率為1 pm，動態范圍為25 dB，掃描頻率為250 Hz。試件表面變厚度復合材料為碳纖維T300/QY8911(材料參數如表1所示)，采用單向帶制造，鋪層厚度如圖3所示為45 mm～47.5 mm，尺寸為600 mm×300 mm，金屬固支架邊框寬度為40 mm。表面粘貼的6個光纖光柵傳感器柵長為10 mm，傳感器排布如圖4所示，傳感器波長與位置見表2。圖3中斜線所示區域為240 mm×200 mm沖擊實驗區域，劃分的網格大小為40 mm×40 mm，如圖4所示。手持式沖擊錘能量三檔可調(1 J、2 J、3 J)，可對試件任意位置進行沖擊。沖擊實驗系統通過監測FBG傳感器中心波長偏移值采集沖擊響應信號，當沖擊錘在試件上進行沖擊，解調儀將同時連接的6個傳感器采集到的沖擊信號傳輸到計算機中。

圖2 基于光柵傳感器的機翼油箱沖擊監測系統Fig.2 The aerofoil fuel tank impact monitoring system based on optic-fiber grating sensors

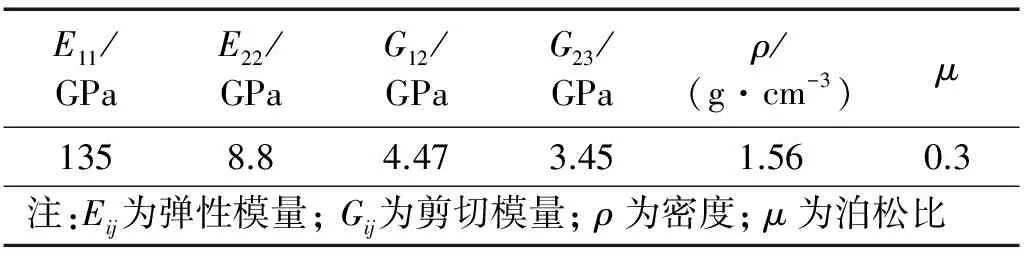
表1 復合材料T300/QY8911 材料參數Tab.1 Material parameters of composite T300/QY8911

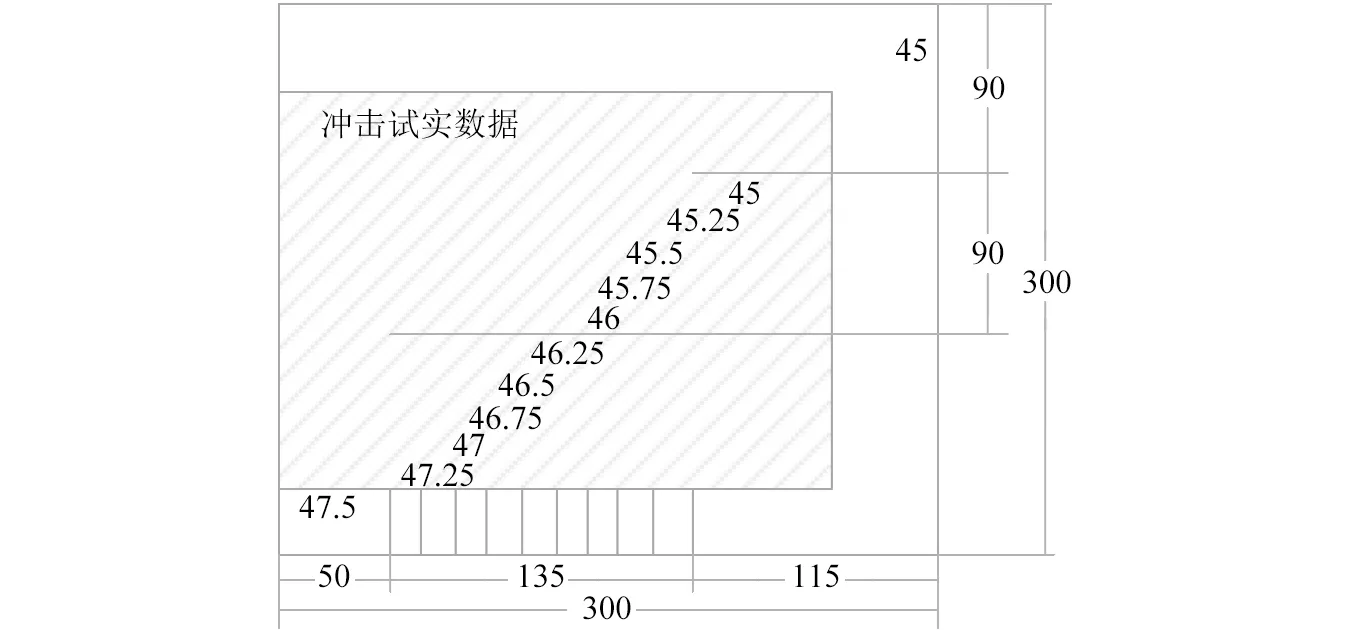
圖3 試件表面1/2復合材料板的鋪層厚度變化圖(mm)Fig.3 The thickness variation of test-piece with 1/2 composite laminate layer(mm)

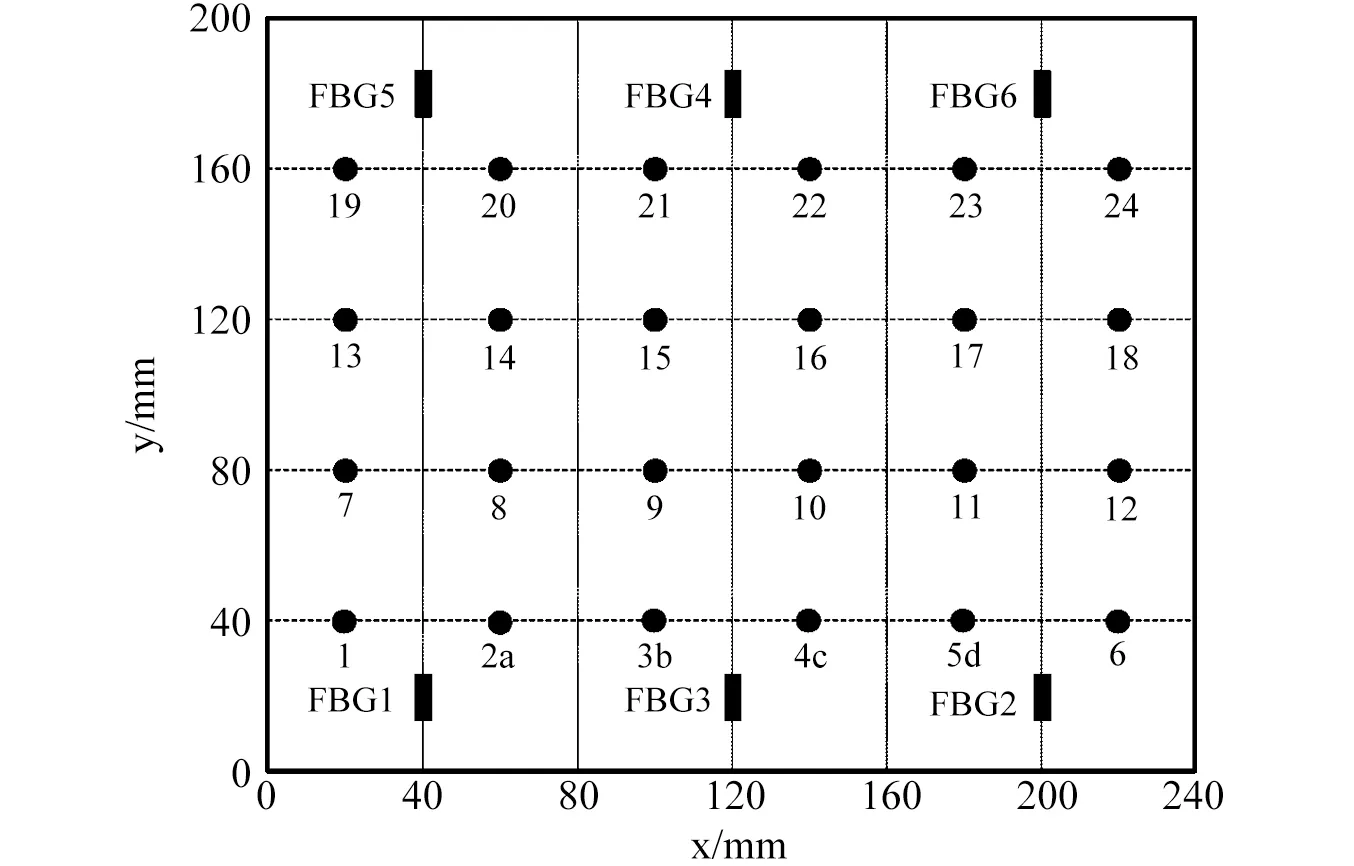
圖4 沖擊點和傳感器位置示意圖Fig.4 Impact positions and sensor positions

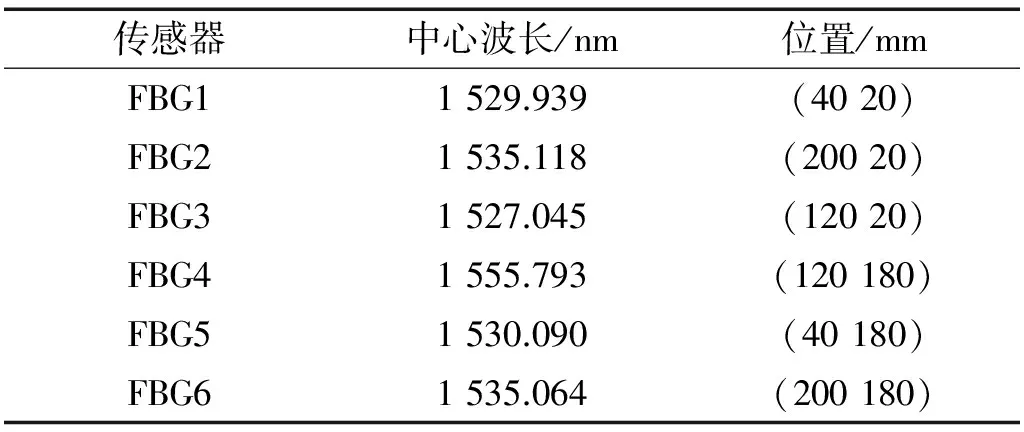
表2 光柵波長與位置Tab.2 Wavelength and position of grating sensors

2.2 建立沖擊樣本信號庫

為了建立用于沖擊能量識別的變厚度復合材料板樣本信號庫，使用沖擊錘分別對沖擊實驗區域的24個網格線中心點進行沖擊，沖擊能量為1 J、2 J、3 J，如圖4所示。每個樣本信號采用250 Hz采樣率采集0.4 s，即采樣次數為100次，所得頻率圖范圍為0～125 Hz。如圖5為6個FBG傳感器采集的沖擊樣本信號示例，以點(60 mm, 40 mm)的沖擊能量1 J、2 J為例。其中該點樣本信號的波形和幅值特征變化都與沖擊能量變化相關，但是通過直接對比沖擊信號時域特征無法識別沖擊能量。

當識別不同沖擊位置的沖擊信號能量時，情況會更為復雜。如圖6為相同沖擊能量、不同沖擊位置時單個傳感器采集的沖擊樣本信號示例，以沖擊能量1 J時點a，b，c，d的信號為例。如圖6(a)所示，沖擊位置和厚度等因素變化使得直接利用時域信號獲得沖擊能量特征值十分困難；如圖6(b)所示，時域信號的傅里葉變換頻譜圖中頻率混疊嚴重。因此需要通過沖擊能量特征提取算法進行分析與識別。

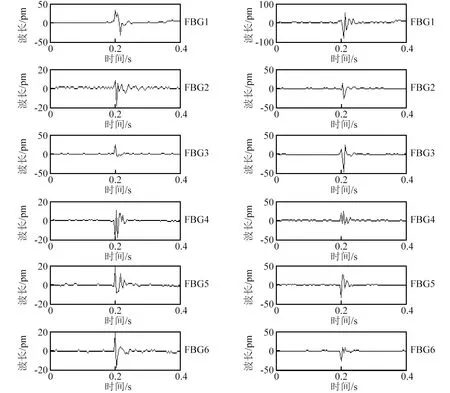
圖5 1 J、2 J沖擊點(60 mm, 40 mm)的傳感網絡信號Fig.5 The signals captured by sensor network during impact process(60 mm, 40 mm)

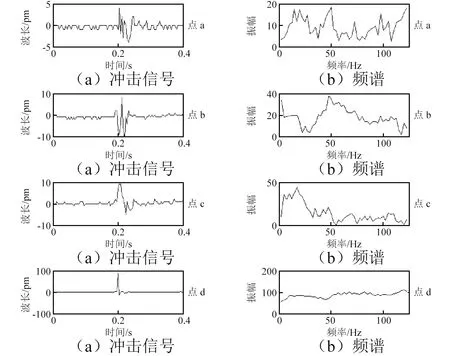
圖6 3號傳感器1 J的沖擊響應信號及頻譜圖Fig.6 Response signal and frequency spectrum of the 3# sensor under 1 J impact

3 實驗結果分析

3.1 建立變厚度板沖擊能量特征集合

因為經典的頻譜分析能提供的有效信號特征信息較少且混疊嚴重，首先利用經典算法EMD和改進算法WEMD對比分析變厚度復合材料板沖擊信號，以圖6中沖擊位置a，c信號為例。

如圖7，8所示為EMD及WEMD算法分解結果，從上自下為分解之后獲得的IMF分量以及1個剩余量。將各階IMF分解量分別與圖6(a)所示的沖擊響應信號進行互相關計算，得到表3及以下結論：WEMD算法的前3階分解量相關系數γ比較大，自第4階分解量開始系數均小于0.1；WEMD算法的所有分量更好的覆蓋了初始信號所在頻段，且獨立性更強。

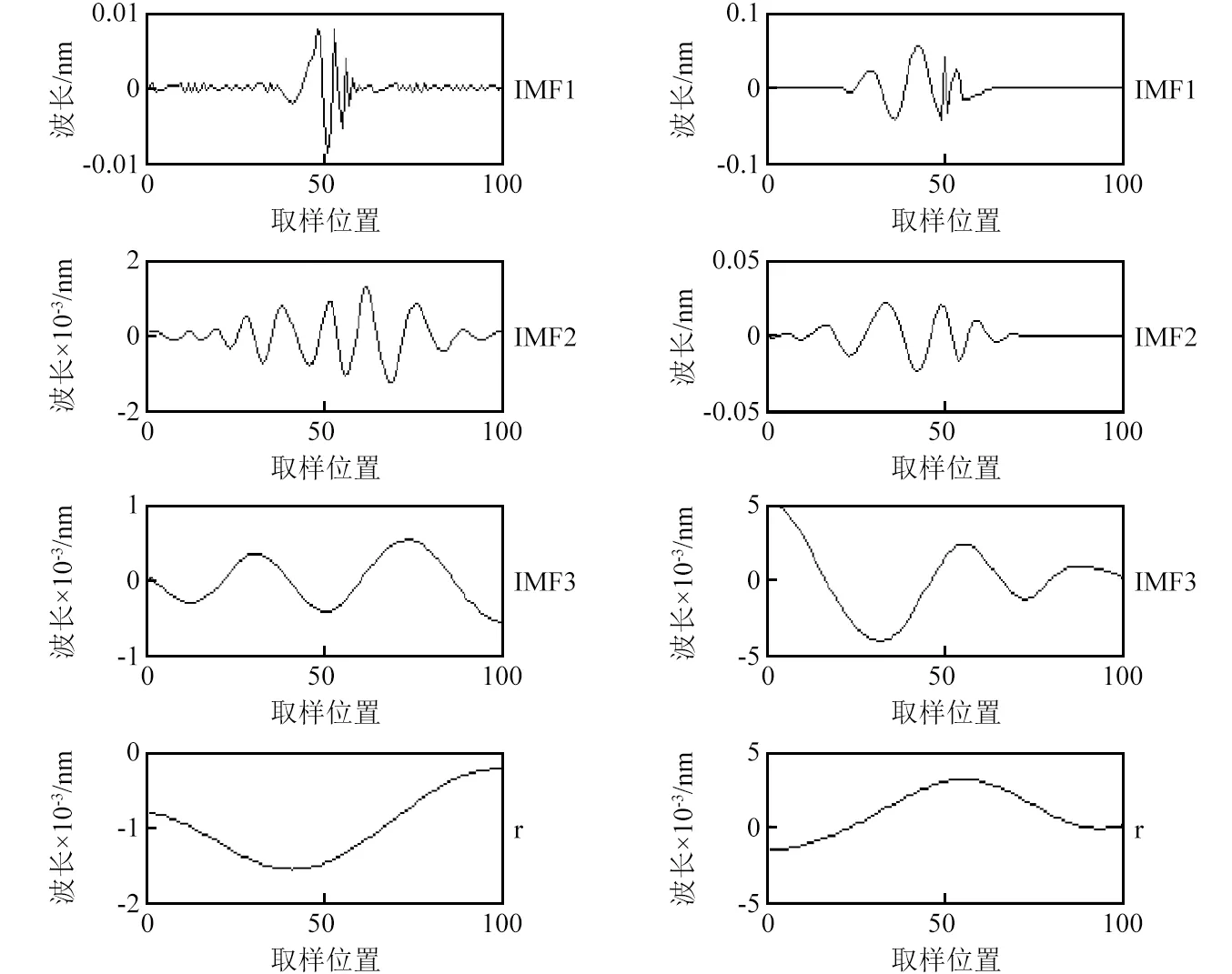
圖7 沖擊點a、c信號的EMD算法分量圖Fig.7 EMD components at position a、c

圖8 沖擊點a、c信號的WEMD算法分量圖Fig.8 WEMD components at position a、c

表3 EMD及WEMD算法各階IMF相關關系表Tab.3 Correlation table of IMF at each order for EMD and WEMD method

對WEMD算法前3階分解量進行頻譜分析，如圖9所示。頻譜圖可以表明：①傳感器頻譜與傳感器位置距離沖擊點的遠近、傳感器所處復合材料層合板位置的厚度變化趨勢基本一致；②頻帶范圍由高頻分量往低頻分量逐漸縮減，且高頻分量的低頻幅值低于低頻分量的對應幅值；③高頻分量的頻譜幅值個數隨著沖擊點位置所處層合板厚度的減少而增加，這與變厚度復合材料板特性有關，例如沖擊點a，c處鋪層厚度分別為47 mm、46 mm，則沖擊信號高頻分量峰值個數分別為4個、7個(界定峰值的閾值為pm/5)。因此，采用改進后的WEMD算法可較好提取變厚度板沖擊能量特征；需選擇頻譜相關性大且混疊較少的分量c3(t)提取頻譜特征峰值pm。

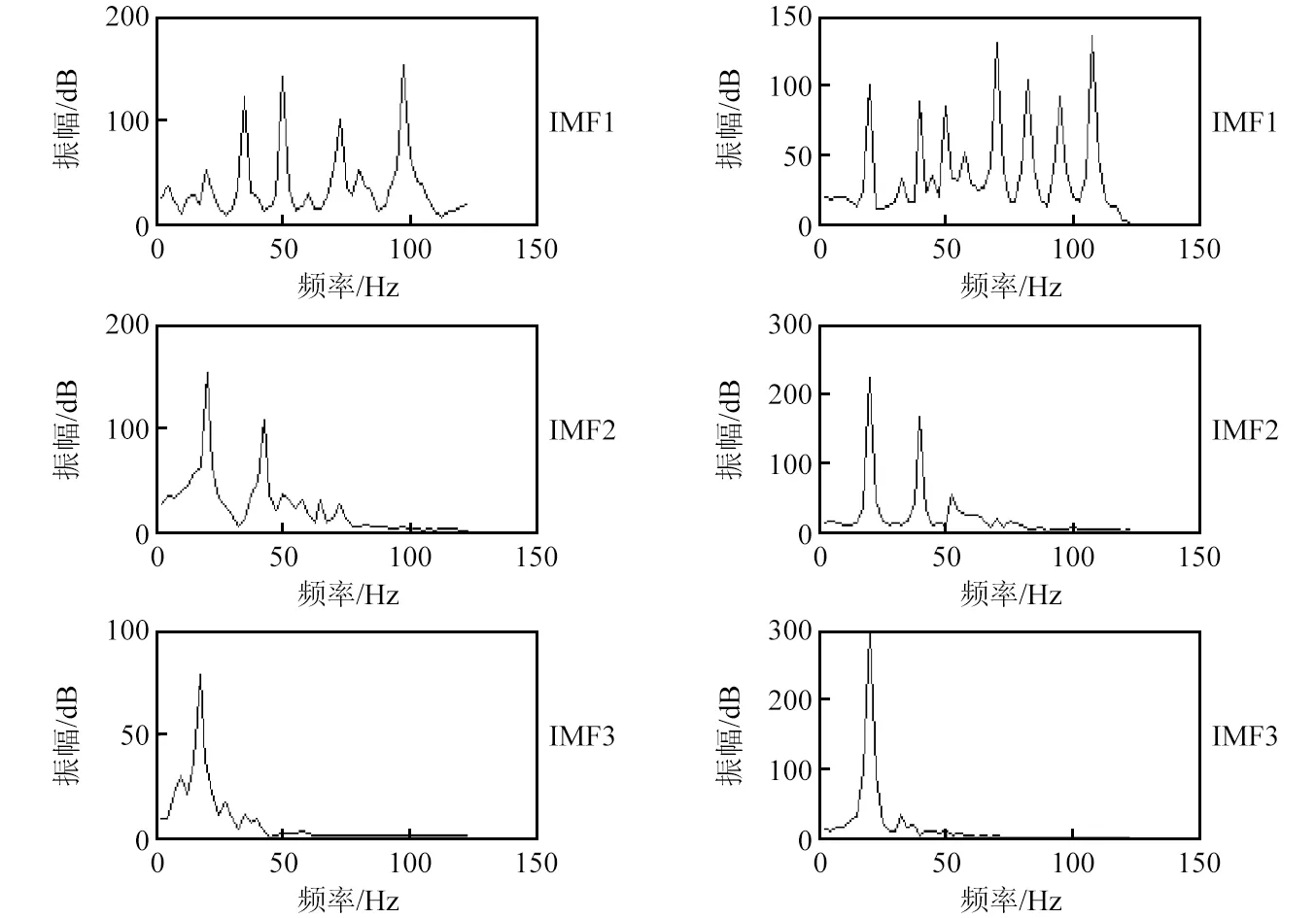
圖9 沖擊點a、c信號WEMD算法前3階分量頻譜圖Fig.9 The first 3 levels of spectrum of signal a、c for WEMD method

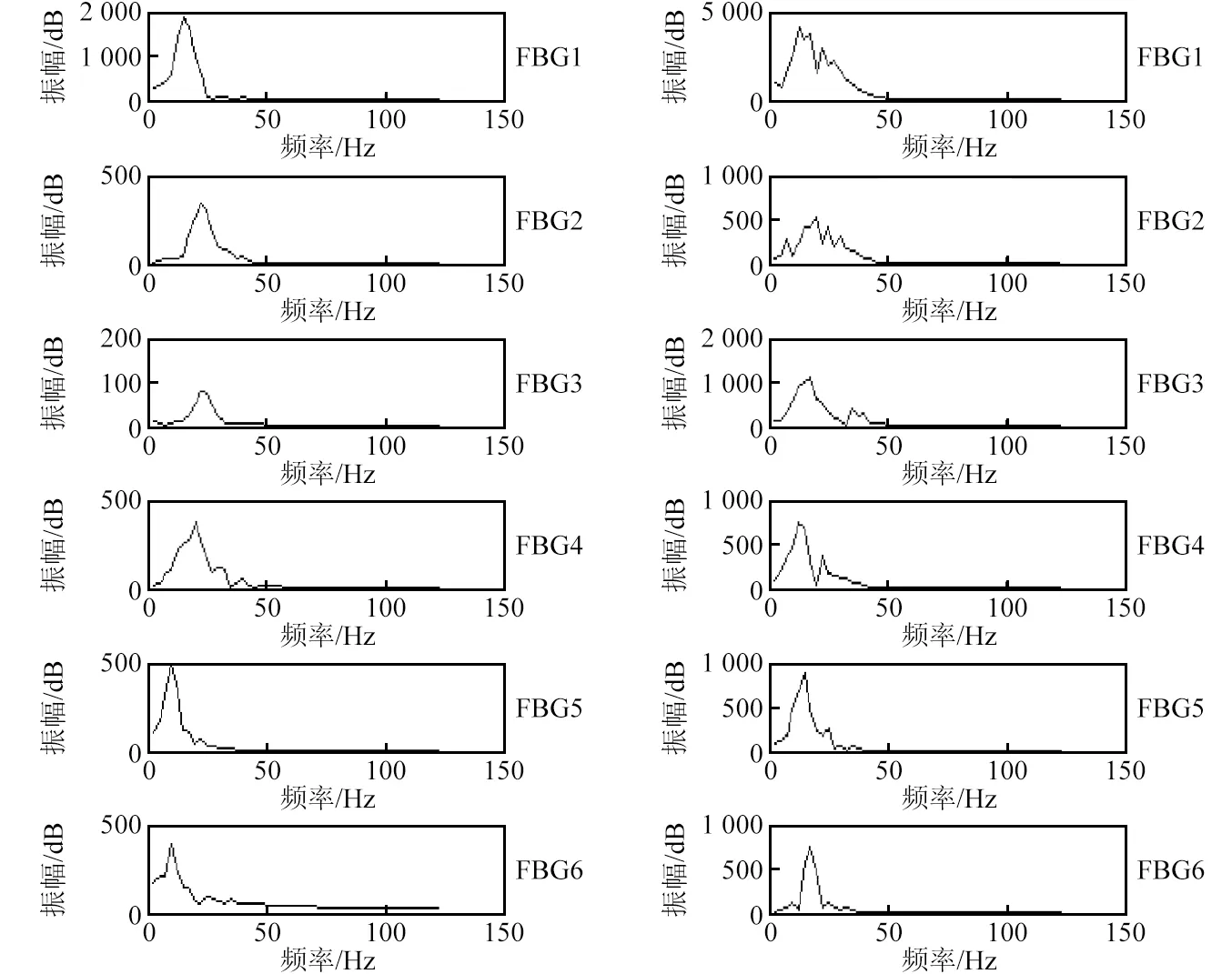
圖10 沖擊點a信號WEMD算法第3階分量頻譜圖Fig.10 The component spectrum at the 3rd order of WEMD method at position a

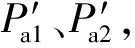
同理，由獲取的所有沖擊樣本信號和識別步驟(1)～(6)可得到1 J～3 J變厚度板沖擊能量特征集合，如表4所示。另外，未利用WEMD算法進行厚度系數修正的普通沖擊能量特征集合，如表5所示。

表4 1、2、3 J變厚度板能量特征值Tab.4 The characteristic value of varied cross-section laminate with energy 1 J、2 J、3 J

表5 1、2、3 J能量特征值Tab.5 The characteristic value of energy 1 J、2 J、3 J

3.2 沖擊能量識別分析

綜合三種沖擊能量的沖擊能量特征集合，得出1 J、2 J、3 J變厚度板沖擊能量特征值范圍分別為(2 120,3 339)、(4 216,4 934)、(6 324,7 410)，而普通沖擊能量特征值范圍分別為(1 870,3 589)、(3 946,5 018)、(5 919,7 537)。為了檢驗此方法的能量識別性能，在變厚度復合材料試件上選擇了30個沖擊點進行了驗證實驗，研究了厚度系數修正對于能量識別性能的影響。其中沖擊點C1-17在大厚度區域，其余的在小厚度區域。識別誤差為實際沖擊能量和預測沖擊能量間的絕對誤差。

圖11和表6顯示了30個沖擊點的沖擊能量識別對比結果。結果表明，厚度系數修正后的識別結果(識別沖擊能量2)比未經修正的結果(識別沖擊能量1)顯示出更好的性能。在未經修正時，驗證點C1(10 mm, 20 mm)和點C22(220 mm, 10 mm)的能量誤差大于0.5個能量等級。如表4、5所示，未經修正的特征集合較為分散，這是由于沖擊位置和對應的沖擊點所在鋪層厚度改變所致，因此未經修正會導致更高的能量誤差。

受到變厚度結構沖擊信號混疊等因素影響，識別結果中大多數驗證點低速沖擊能量特征值介于兩級能量特征集合之間，僅有小厚度區域上驗證點C27(160 mm, 170 mm)、C29(115 mm, 170 mm)和C30(90 mm, 175 mm)的能量特征值在經過厚度系數修正后屬于對應級別能量范圍內。同時，當未經修正時，在大厚度區域上的沖擊相對于小厚度區域顯示出較大的識別誤差。大厚度區域和小厚度區域的平均誤差分別為15.19%、10.09%。大厚度區域的較大誤差點由沖擊信號頻譜幅值的減少造成，這取決于沖擊位置及鋪層厚度，在未經修正的識別情況下誤差更大。因此，可以通過對沖擊信號進行WEMD分解、厚度修正來提升沖擊能量識別性能，厚度系數根據沖擊位置和厚度改變。

從對比結果來看，厚度系數修正方法能夠更準確的評估低速沖擊的實際能量。尤其是低靈敏度的大厚度區域平均誤差從15.19%明顯減少為6.96%。提出的能量識別方法成功識別了所有驗證點1～3 J沖擊能量，其中最大誤差為15.67%，平均誤差為5.5%。

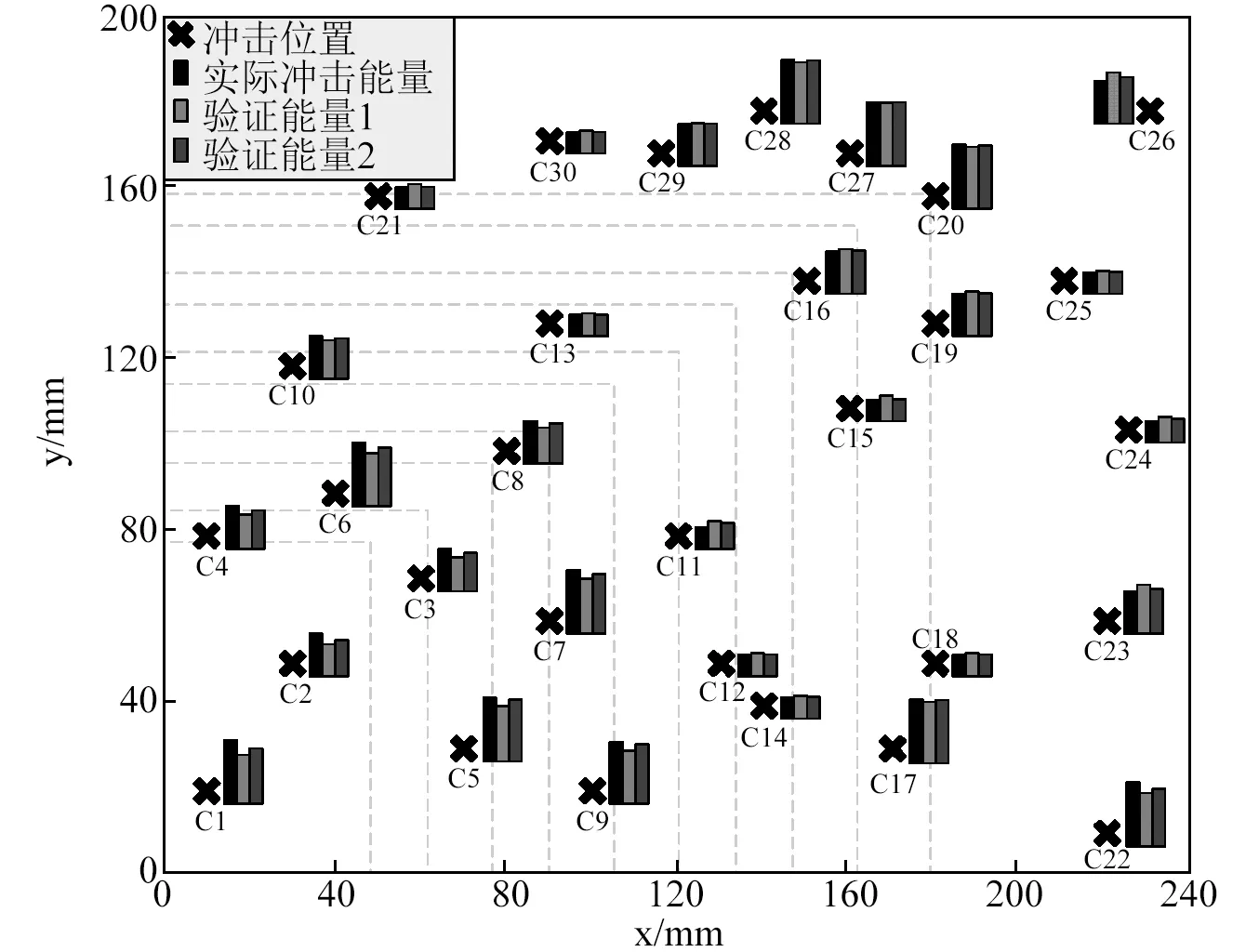
圖11 復合材料板低速沖擊能量驗證實驗結果示意圖Fig.11 The LVI energy discrimination experimental results of composite laminate

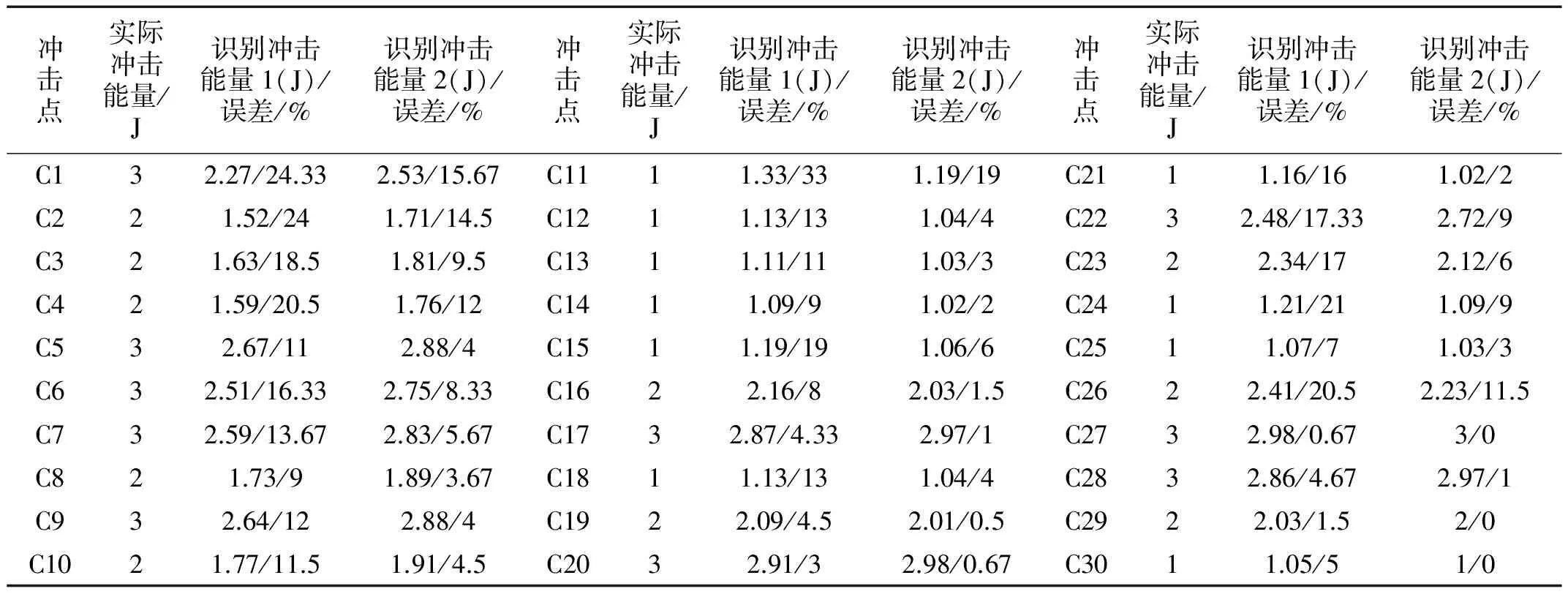
表6 30個驗證點識別結果Tab.6 The discrimination results of 30 testing positions

4 結 論

為了監測復合材料層合板受到的低速沖擊載荷，針對變厚度復合材料結構沖擊信號特性，利用光纖光柵傳感監測技術，提出了基于WEMD算法的沖擊能量識別方法，采用厚度系數修正方法，給出了變厚度復合材料結構沖擊能量識別步驟；采用光纖光柵傳感技術搭建了光纖布拉格光柵沖擊能量監測系統，根據變厚度復合材料結構特性進行了基于WEMD算法的沖擊能量特征提取，并針對變厚度試件1 J、2 J、3 J沖擊能量信號建立了變厚度板沖擊能量特征集合并進行能量識別驗證實驗。結果表明：

(1)采用改進后的WEMD分解算法，可以有效避免高頻固有模態信號的模態混疊，提升了沖擊特征值有效性，增加了能量識別準確性，可較好的提取變厚度板沖擊能量特征。

(2)搭建了變厚度復合材料結構低速沖擊能量識別系統，該系統保證了沖擊能量識別方法的有效性，并具有可靠穩定、抗干擾、分布式等優勢。

(3)通過實驗驗證了提出的沖擊能量識別方法的性能。實驗證明，該方法可以準確評估1～3 J沖擊能量，其中最大誤差為15.67%，平均誤差為5.5%，識別結果符合工程應用范圍。厚度系數修正步驟(尤其在大厚度區域)顯著提升了識別性能，其中識別平均誤差由15.19%明顯減少為6.96%。

參 考 文 獻

[1] HU Z Y, HU Y F.Dynamic monitoring the strain of composites due to high speed collisions using fiber bragg grating network[J].Mechanika, 2012, 18(1): 35-39.

[2] 江大志, 郭洋, 李長亮, 等.雙層夾芯復合材料結構橫向沖擊響應實驗[J].爆炸與沖擊, 2009, 29(6): 590-595.

JIANG Dazhi, GUO Yang, LI Changliang, et al.Experimental investigation on response of two-core sandwich composite structures under transverse impact[J].Explosion and Shock Waves, 2009, 29(6): 590-595.

[3] 馮勇明, 周麗.基于匹配追蹤算法的復合材料沖擊損傷成像技術[J].爆炸與沖擊, 2012, 32(3):259-266.

FENG Yongming, ZHOU Li.Impact damage imaging for composites based on matching pursuit method[J].Explosion and Shock Waves, 2012, 32(3):259-266.

[4] TAKEDA S, AOKI Y, NAGAO Y.Damage monitoring of CFRP stiffened panels under compressive load using FBG sensors[J].Composite Structures, 2012, 94(3): 813-819.

[5] 李戈嵐, 吳斌.復合材料變厚度加筋板后屈曲耐久性/損傷容限一體化設計研究[J].飛機設計, 2007, 27(5): 24-30.

LI Gelan, WU Bin.Study of post-buckling durability/damage tolerance design of variable thickness composite stiffened panel[J].Aircraft Design, 2007, 27(5): 24-30.

[6] 馬靜敏, 任勇生, 姚文莉.復合材料變截面旋轉薄壁懸臂梁自由振動分析[J].工程力學, 2013, 30(1): 37-44.

MA Jingmin, REN Yongsheng, YAO Wenli.Free vibration analysis of rotating composite thin-walled cantilever beams with variable closed-section[J].Engineering Mechanics, 2013, 30(1): 37-44.

[7] 郭飛, 張培偉, 張大海, 等.基于小波包能量特征向量的光纖布拉格光柵低速沖擊定位[J].振動與沖擊, 2017, 36(8): 184-189.

GUO Fei, ZHANG Peiwei, ZHANG Dahai, et al.Localization of low-velocity impact by using fiber Bragg grating sensors based on wavelet packet energy eigenvector[J].Journal of Vibration and Shock, 2017, 36(8): 184-189.

[8] FRIEDEN J, CUGNONI J, BOTSIS J, et al.Low energy impact damage monitoring of composites using dynamic strain signals from FBG sensors-Part II: Damage identification[J].Composite Structures, 2012, 94(2): 593-600.

[9] JANG B W, LEE Y G, KIM C G, et al.Impact source localization for composite structures under external dynamic loading condition[J].Advanced Composite Materials, 2015, 24(4): 359-374

[10] 路士增, 林蘭波, 姜明順, 等.基于光纖光柵傳感器的復合材料損傷識別系統[J].光學精密工程, 2014, 22(11): 2894-2901.

LU Shizeng, LIN Lanbo, JIANG Mingshun, et al.Identification system of composite material damage based on FBG sensor[J].Optics and Precision Engineering, 2014, 22(11): 2894-2901.

[11] 蘆吉云, 王幫峰, 梁大開.基于小波包特征提取及支持向量回歸機的光纖布拉格光柵沖擊定位系統[J].光學精密工程, 2012, 20(4): 712-718.

LU Jiyun, WANG Bangfeng, LIANG Dakai.Identification of impact location by using FBG based on wavelet packet feature extraction and SVR[J].Optics and Precision Engineering, 2012, 20(4): 712-718.

[12] KIRIKERA G R, BALOGUM O, KRISHNASWAMY S.Adaptive fiber Bragg grating sensor network for structural health monitoring: Applications to Impact Monitoring[J].Structural Health Monitoring, 2011, 10(1): 5-16.

[13] 陳勇, 王坤, 劉煥淋, 等.三點尋峰算法處理光纖布拉格光柵傳感信號[J].光學精密工程, 2013, 21(11): 2751-2756.

CHEN Yong, WANG Kun, LIU Huanlin, et al.Processing FBG sensing signal with three-point peak-detection algorithm[J].Optics and Precision Engineering, 2013, 21(11): 2751-2756.

[14] DJINOVIC Z, SCHEERER M, TOMIC M.Impact damage detection of composite materials by fiber Bragg gratings[J].Proceedings of SPIE-Smart Sensors, Actuators, And Mems V, 2011, 8066(3): 487-504.

[15] FRIEDEN J, CUGNONI J, BOTSIS J, et al.Low energy impact damage monitoring of composites using dynamic strain signals from FBG sensors-Part I: Impact detection and localization[J].Composite Structures, 2011, 94(2): 438-445.

[16] DU Qiuhua, YANG Shunian.Application of the EMD method in the vibration analysis of ball bearings[J].Mechanical Systems and Signal Professing, 2007, 21(6): 2634-2644.

[17] 黎恒, 李智, 莫瑋.低采樣率下經驗模態分解性能提升研究[J].振動與沖擊, 2016, 35(17): 185-190.

LI Heng, LI Zhi, MO Wei.Performance improvement of EMD under low sampling rates[J].Journal of Vibration and Shock, 2016, 35(17): 185-190.