材料屬性溫度相關變厚度FGM圓板自由振動DQM求解

李清祿，王文濤，楊靜寧

(蘭州理工大學 理學院工程力學系，蘭州 730050)

為滿足材料能夠抵抗高溫環境,日本科學家在80年代制造了功能梯度材料(Functionally Graded Material, FGM)[1]。功能梯度材料通常是由陶瓷和金屬構成的復合材料，其材料性能從一側到另一側連續梯度變化。這種連續的空間變化的成分設計，可以減輕應力集中附近的空隙、缺陷或對材料進行優化，以達到預期的工程目標。功能梯度材料具有巨大的潛在的技術和工程應用，特別是在極端熱環境下，可以明顯減少由于高溫梯度引起的應力集中。

目前，就功能梯度材料的熱屈曲和自由振動做了大量的研究[2]。Yang等[3]基于高階板理論，研究了功能梯度薄圓板的熱屈曲行為，獲得了熱臨界溫度的封閉解。Yang等[4]采用高階剪切理論，研究了非均勻升溫下矩形板的非線性彎曲和過屈曲問題，并對帶有裂紋FGM梁受到軸向載荷和移動載荷作用下的自由和受迫振動作了分析。Li等[5]采用打靶法研究了具有初始缺陷FGM圓板的熱后屈曲行為。Kermani等[6]利用三維彈性理論建立了FGM圓板和圓環板的自由振動控制方程，利用微分求積法求解了問題的數值解，討論了厚徑比和梯度指數對無量綱頻率的影響。Mantari等[7]基于廣義準三維混合高階剪切變形理論，研究了彈性地基上功能梯度矩形板的自由振動響應。以上文獻都沒有考慮材料物性參數的溫度相關性。Reddy等[8]表明，FGM材料的物性參數與溫度變化是相關的。

Malekzadeh等[9]利用微分求積法研究了雙參數彈性地基上FGM薄至中厚環板在熱環境中的自由振動問題。Yang等[10]研究了剪切變形圓/環板的熱后屈曲行為，其中精確考慮了溫度對物性參數的依賴性。Shen等[11]考慮了材料物性參數的溫度相關性，分別采用Voigt混合率模型和Mori-Tanaka模型研究了熱環境中FGM矩形板的自由振動。Shen等[12]考慮了材料的溫度相關性，研究了彈性地基上FGM圓柱曲板在徑向壓力下的熱屈曲問題。

由于制造技術和材料科學的發展,人們能將圓板加工成各種變厚度的圓板以滿足航空航天等工程領域的要求，目的是減輕自重和幾何尺寸。由于FGM材料的興起，變厚度FGM結構廣泛應用于航空航天、土木以及核工業等領域，因此變厚度FGM結構的力學行為的研究具有現實的工程背景。然而文獻調研所知，材料屬性溫度相關變厚度FGM圓板自由振動的研究目前在國內外還沒有相關的報道。

本文研究了變厚度Mindlin功能梯度材料圓板在熱環境中的橫向自由振動問題。假設材料屬性溫度相關且材料組分研板的厚度按冪指數梯度連續變化。基于一階剪切板理論，利用哈密頓原理建立了以中面轉角和橫向位移為基本未知量的FGM變厚度圓板軸對稱自由振動問題的控制微分方程。采用微分求積法將微分方程組轉化為自由振動代數方程，求解特征值問題從而求得自由振動的前幾階頻率，并與已有的各向同性材料圓板以及FGM圓板的無量綱頻率進行了比較，證實所得的結果的可靠性。給出了均勻升溫和非均勻升溫兩種情況下，板的厚度、材料梯度指數以及厚度變化系數不同時的固有頻率。詳細討論了材料梯度指數、厚度變化系數、溫度變化以及邊界條件對頻率的影響。

1 FGM物性參數及溫度場描述

1.1 物性參數描述

考慮FGM材料板為陶瓷ZrO2和金屬Ti-6Al-4V復合而成，板的下面為純陶瓷，陶瓷材料的體積分數可用下面的表達式給出

(1)

式中：p代表FGM從上表面過渡到下表面的梯度指標。p=0代表純陶瓷材料，隨著p的增加，板內陶瓷材料的成分逐漸減少,金屬(Ti-6Al-4V)直到變成純金屬。

采用Voigt等應變的線性混合率模型，則FGM材料的等效物性參數彈性模量E、密度ρ、泊松比υ、熱膨脹系數α、熱傳導系數K是依賴于溫度T的，可描述為

E(z,T)=Em+(Ec-Em)(0.5+z/h)p

(2)

ρ(z,T)=ρm+(ρc-ρm)(0.5+z/h)p

(3)

υ(z,T)=υm+(υc-υm)(0.5+z/h)p

(4)

α(z,T)=αm+(αc-αm)(0.5+z/h)p

(5)

K(z,T)=Km+(Kc-Km)(0.5+z/h)p

(6)

1.2 溫度場描述

考慮材料物性參數P與溫度相關[13]

P=P0(P-1T-1+1+P1T+P2T2)

(7)

式中：T=T0+ΔT，室溫T0=300K。材料隨溫度變化的物性參數，如表1所示[11]。記陶瓷一側和金屬一側的溫度分別為Tc和Tm，板內溫度沿厚度變化。其中升溫滿足一維熱傳導方程

(8)

邊界條件為

T(h/2)=Tc,T(-h/2)=Tm

(9)

方程(8)在邊界條件(9)下的冪級數形式的解為

其中

Tr=Tc/Tm,Kcm=Kc-Km

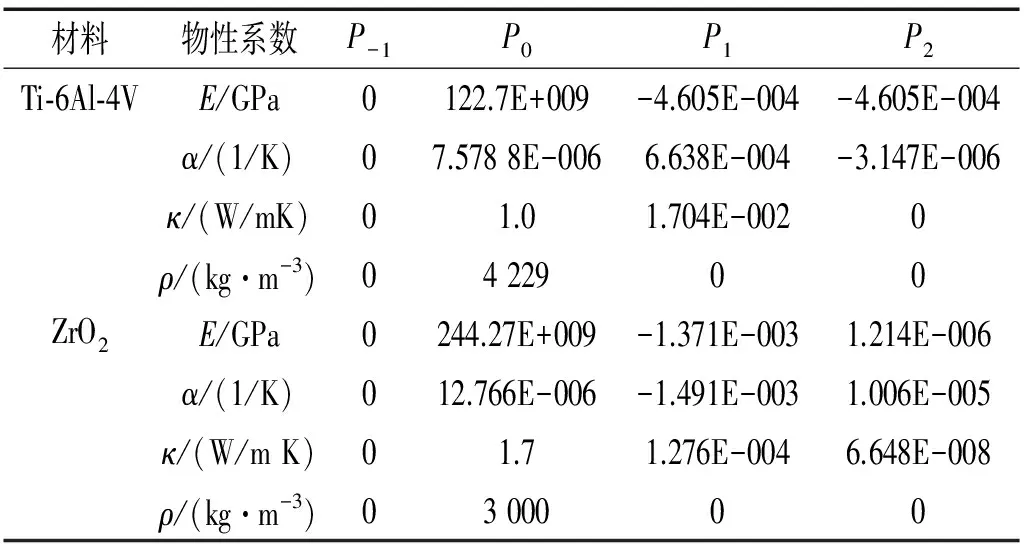
表1 陶瓷和金屬隨溫度變化的物性系數Tab.1 Temperatur-dependent coefficients for ceramic and metals

2 控制微分方程

考慮一半徑為a,變厚度h(r)的FGM中厚圓板。厚度從板中心到外邊界按線形變化h(r)=h0+λr。其中，h0為板中心處的厚度，λ為厚度變化系數。在板上施加沿厚度方向變化的溫度場T。采用極坐標系(r,θ,z)，r，θ和z分別為徑向、環向和橫向坐標。

考慮軸對稱自由振動，根據一階剪切板理論，其位移場可寫為

(10)

式中：w為板橫向位移；ψ為板中面法線的轉角；t為時間變量。

幾何方程：

(11)

物理方程：

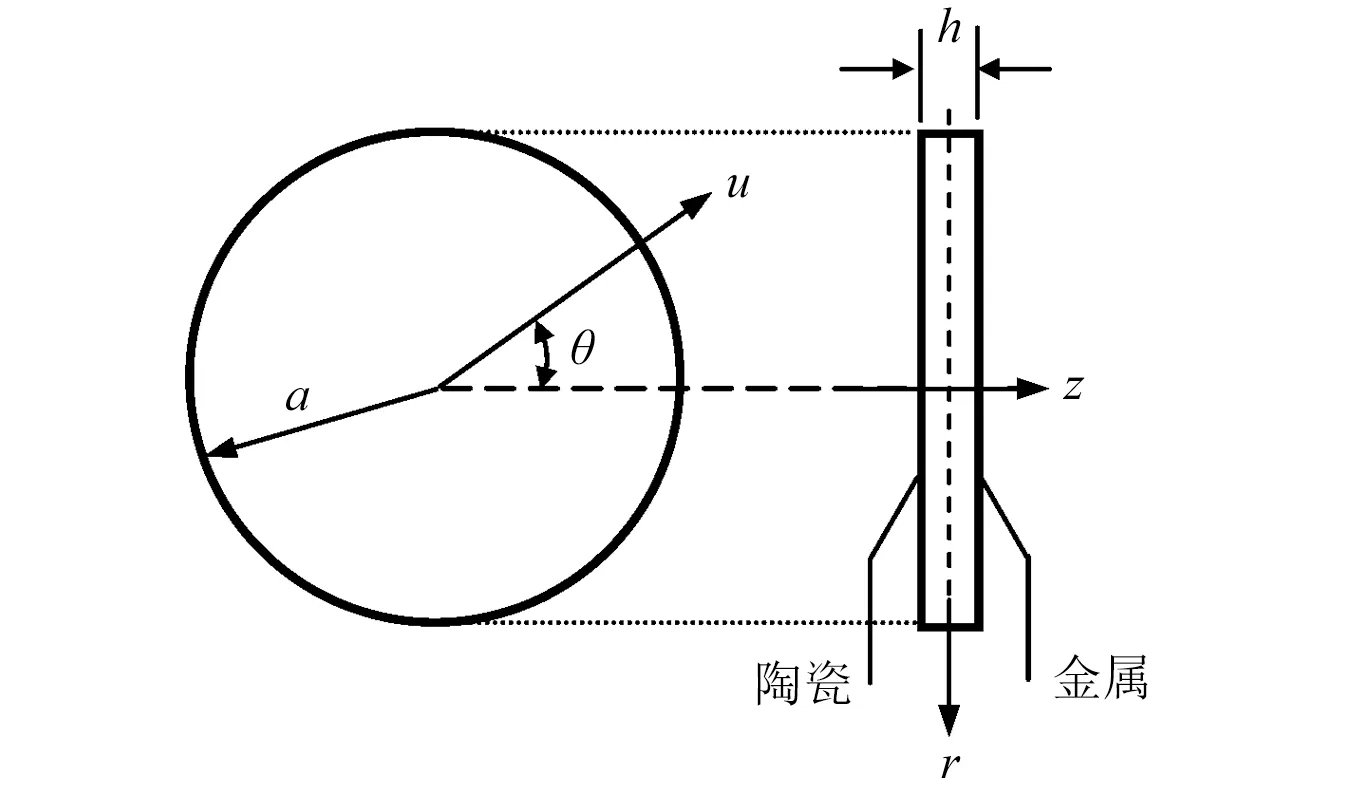
圖1 FGM圓板示意圖Fig.1 Sketch map of the FGM circular plate

將式(11)代入式(12)，并沿厚度方向積分，可得內力為

(13)

Mindlin板的剪切系數為κs=12/π2。

式(13)中剛度系數的定義為

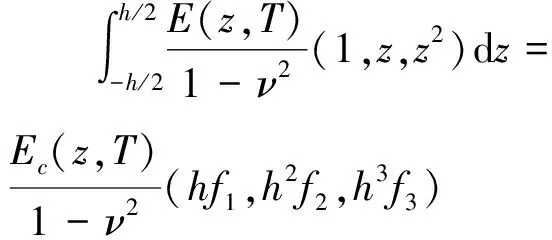
(14)

熱軸力和熱彎矩為

(15)

運動方程：

應變能變分為

(16)

動能變分為

(17)

由Hamilton原理，由

(18)

將式(13)代入式(18),可得位移形式的控制方程

(19)

假設板振動的位移和轉角均為時間的諧響應模態

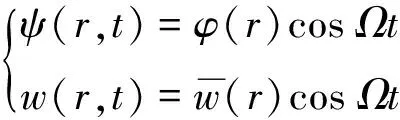
(20)

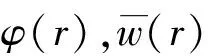
將式(20)代入式(19)，可得位移形式的運動控制方程如下

(21)

(22)

其中

為計算方便，采用如下量綱一變換

得FGM Mindlin圓板軸對稱振動無量綱控制方程為

(23)

考慮傳統的兩種邊界條件,

(1)周邊夾緊

(24a)

(2) 周邊不可移簡支

(24b)

3 DQM方程的離散

按照DQM方法的原理,沿徑向方向0≤r≤R將半徑劃分N個節點,本文采用非均勻節點劃分方式

(25)

由微分求積法，一階導數權系數為

類似地，二階及二階導數權系數為

控制方程(23)和邊界條件(24a),(24b)通過DQM離散后，可得下面的代數方程組

k=2,3,…N-1

(26)

周邊夾緊

(27a)

周邊不可移簡支

(27b)

這樣，變厚度FGM圓板在熱環境中自由振動的控制方程(26)與邊界條件(27a),(27b)就構成了征值方程，可用分塊矩陣象征性表示為

其中

{Xb}=[W1,WN,φ1,φN]T

{Xi}=[W2,W2,…WN-1,φ2,φ3,φN-1]T

(28)

利用式(26)消去{Xb}可得特征值方程

(29)

4 數值結果及分析

首先，將對DQM結果的收斂性進行討論。計算中取p=0，λ=0，Tc=Tm=0K，則FGM圓板退化為均勻各項同性等厚度圓板的自由振動問題。對于給定的不同節點N，表2給出了固支邊界下圓板的前三階量綱一固有頻率，并和文獻[14]三維彈性解和文[15]的解析解進行了比較，從計算結果看出，取9個節點計算的結果已和文獻結果十分接近。當節點數超過13時，DQM計算的結果載不增加了。這說明，13個節點就可以得到足夠精確的數值解答。表3為N=13時的計算結果，并與文獻[14-15]作了比較，其結果十分吻合。因此，后面的計算都取13個節點。用DQM法取較少的節點數就能得到精度比較高的結果，費時少而精度高。

表4給出了FGM圓板的計算結果的比較情況,取等厚度圓板δ=0.01,λ=0,p=0,0.1,1,5時，FGM圓板在無升溫下軸對稱自由振動的前三階量綱一固有頻率。從表4可以看出，本文的計算結果和文獻[16]給出的FGM圓板的結果非常接近,說明本文方法的正確性和DQM方法的適用性。

表5和表6分別給出了固支和簡支兩種邊界下，厚度變化系數λ=0時，不同梯度指標p下Mindlin圓板在不同均勻升溫下的前三階量綱一頻率。表5不難看出，對于固支圓板，δ一定時板的前三階固有頻率均隨p的增加而降低，p一定時板的前三階頻率均隨厚度δ的增加而減小，這一結論和文獻[17]給出的結果是相似的，但由于均勻升溫導致了相同條件下的固有頻率和文獻[17]相比減小了。同時看出，固有頻率隨升溫的升高會降低。從表6反映出，簡支板的二階和三階頻率隨p和δ的增加都會減小，但一階頻率卻并非如此，這和文獻[17]給出的無溫度作用下的情況是相反的。

圖2～圖4分別給出了固支邊界下,λ=0.05時,前三階量綱一頻率在不同非均勻升溫下隨梯度指標p的變化關系圖。由圖可見，隨非均勻升溫的增加固有頻率單調減小。圖5為截面變化系數λ對前三階頻率的影響曲線，可見，隨λ的增加一階頻率單調增加，二、三階頻率單調減小。

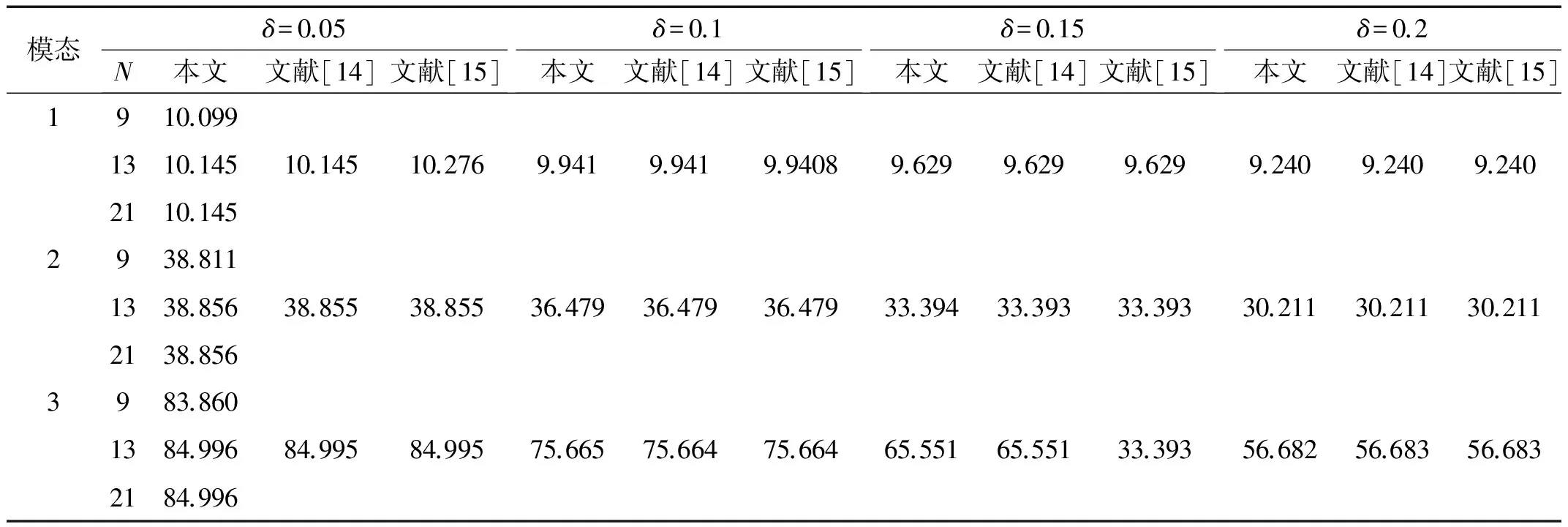
表2 固支板自由振動量綱一頻率ω(p=0)Tab.2 Dimensionless natural frequencies ω of vibration for Mindlin plates with clamped edge

表3 簡支板自由振動量綱一頻率ω(p=0)Tab.3 Dimensionless natural frequencies ω of vibration for Mindlin plates with simply supported edge

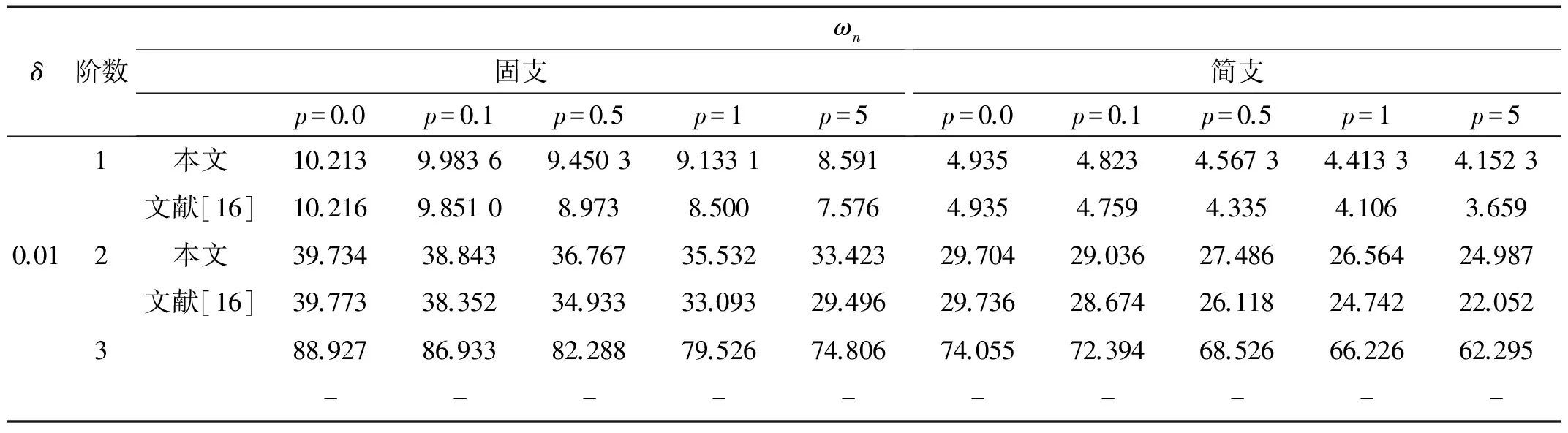
表4 不同梯度指標p下圓板自由振動量綱一頻率ωTab.4 Dimensionless natural frequencies ωn of FGM Mindlin plates with different graded index

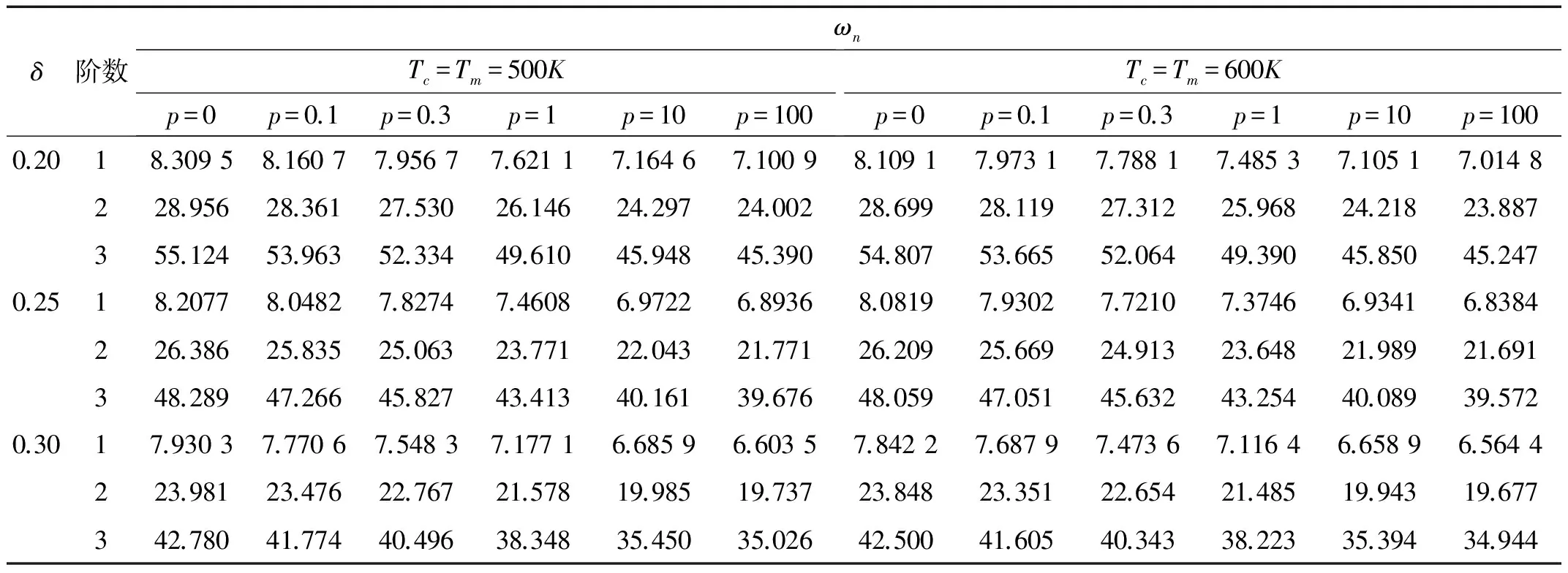
表5 均勻升溫下周邊固支FGM圓板自由振動量綱一固有頻率ωnTab.5 Dimensionless natural frequencies ωn of FGM circular plates subjected to uniform temperature with clamped edge

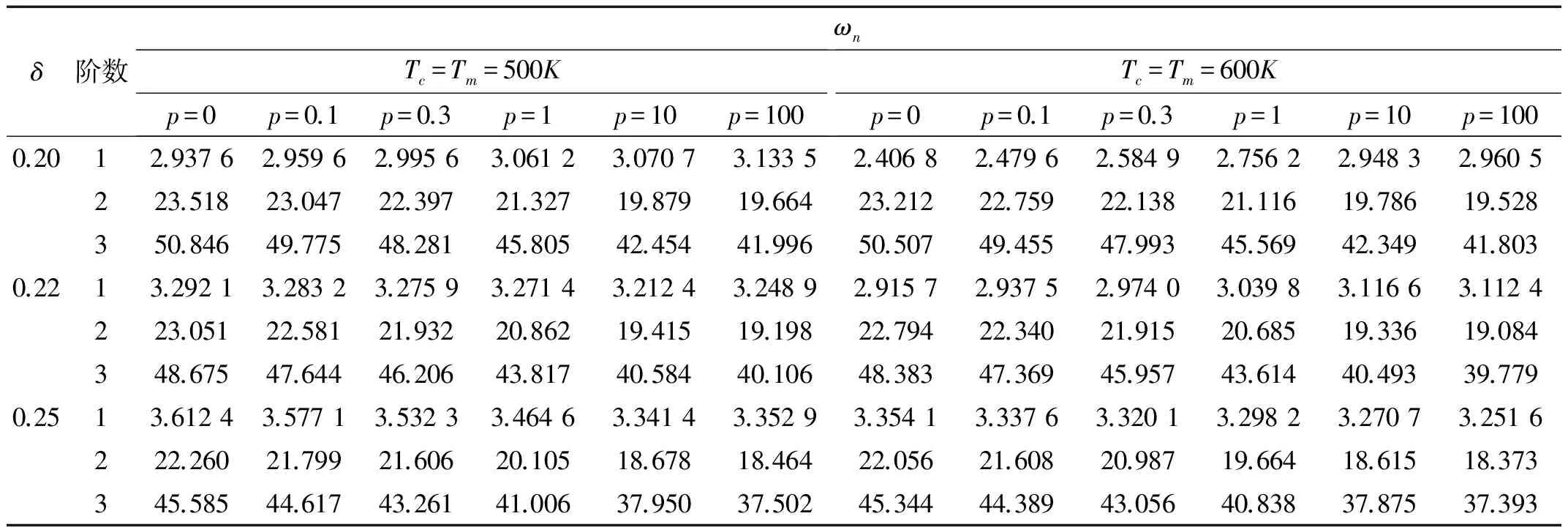
表6 均勻升溫下周邊簡支FGM圓板自由振動量綱一固有頻率ωnTab.6 Dimensionless natural frequencies ωn of FGM circular plates subjected to uniform temperature with simply supported edge

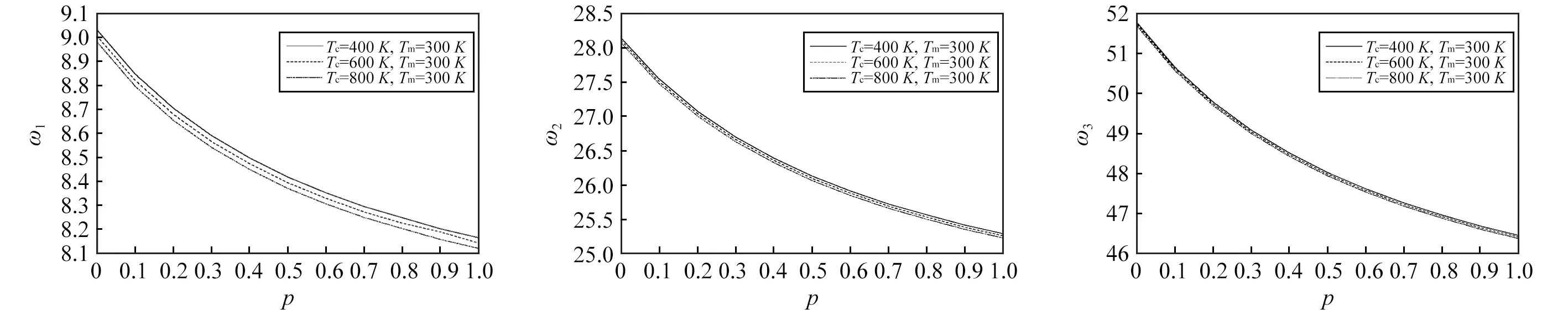
圖2 周邊固定時非均勻升溫時對一階頻率與梯度指數關系的影響 圖3 周邊固定時非均勻升溫時對二階頻率與梯度指數關系的影響 圖4 周邊固定時非均勻升溫時對三階頻率與梯度指數關系的影響 Fig.2 Effect of uniform temperature rise on material constant vs.fundamental frequency with clamped edge Fig.3 Effect of uniform temperature rise on material constant vs.second-mode frequency with clamped edge Fig.4 Effect of uniform temperature rise on material constant vs.third-mode frequency with clamped edge

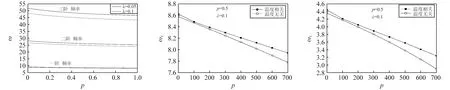
圖5 不同梯度指數下厚度變化系數對FGM圓板一階頻率的影響 圖6 周邊固定下非均勻升溫對前三階頻率的影響 圖7 周邊簡支下非均勻升溫對FGM圓板一階頻率的影響Fig.5 Effect of thickness variation coefficient on the first three frequencies under different material of the material constant Fig.6 The influence of temperature dependence f the material properties on the fundamental frequency of the clamped FGM plates subjected non-uniform temperature rise Fig.7 The influence of temperature dependence of the material properties on the fundametal frequency of the simply supported FGM plates subjected to non-uniform temperature rise

圖6和圖7分別給除了周邊固定和簡支條件下，取梯度指標p=0.5,中心厚度和半徑比δ=0.2,厚度變化系數λ=0.1情況下均勻升溫和非均勻升溫對一階固有頻率的影響。可以看出，溫度變化對板固有頻率有較大影響，且這種影響隨升溫的增加而顯著增加。考慮材料屬性溫度相關下的固有頻率略高于不考慮溫度相關下的。

4 結 論

基于一階剪切理論，研究了功能梯度變厚度圓板在熱環境中的軸對稱自由振動。其中假設材料梯度僅沿厚度呈冪指數變化且物性參數與溫度相關，利用哈密頓原理推導了以中面轉角和橫向位移為基本未知量的自由振動問題的控制方程。利用DQM法求解了周邊固定和簡支兩種邊界條件下的自由振動無量綱頻率，將得到的結果與均勻以及FGM材料圓板已有結果進行了比較，顯示了本文方法的正確性。數值結果表明:

(1) 均勻和非均勻升溫下，固支和簡支圓板的無量綱頻率都隨梯度指數的增加而減小。同樣條件下，固支圓板的頻率高于簡支圓板的頻率。

(2) 均勻升溫下，FGM固支圓板的無量綱頻率隨隨厚徑比的增加而減小，但FGM簡支圓板的無量綱頻率并非如此。

(3) 隨均勻和非均勻升溫的增加，FGM圓板無量綱頻率都減小，非均勻升溫下的頻率高于均勻升溫下的。

(4) 隨變厚度系數的增加，無量綱頻率減小。考慮溫度相關時的頻率略高于溫度無關時的頻率。

參 考 文 獻

[1] KOIZUMI M.The concept of FGM ceramic transitions [J].Functionally Gradient Materials，1993,34:3-10.

[2] 仲政, 吳林志, 陳偉球.功能梯度材料與結構的若干力學問題研究進展[J].力學進展, 2010, 40(5): 528-541.

ZHONG Zheng, WU Linzhi, CHEN Weiqiu.Progress in the study on mechanics problems of functionally graded materials and structures [J].Advances in Mechanics, 2010, 40(5): 528-541.

[3] YANG J, SHEN H S.Non-linear analysis of functionally graded plates under transverse and in plane loads [J].International Journal of Non-linear Mechanics, 2003,38(4): 467～482.

[4] YANG J, SHEN H S.Nonlinear bending analysis of shear deformable functionally graded plates subjected to thermo-mechanical loads under various boundary conditions[J].Composites Part B: Engineering,2003,34:103-115.

[5] LI S R, ZHANG J H, ZHAO Y G.Nonlinear thermomechanical post-buckling of circular FGM plate with geometric imperfection?[J].Thin-Walled Structures, 2007, 45(5): 528-536.

[6] KERMANI I D, GHAYOUR M, MIRDAMADI H R.Free vibration analysis of multi-directional functionally graded circular and annular plates[J].Journal of Mechanical and Technology, 2012, 26(11): 3399-3410.

[7] MANTARI J L.Free vibration of advanced composite plates resting on elastic foundations based on refined non-polynomial theory[J].Meccanica, 2015, 50: 2369-2390.

[8] REDDY J N, CHIN C D.Thermoelastical analysis of functionally graded cylinders and plates[J].Journal of Thermal Stresses, 1998, 21: 593-626.

[9] MALEKZADEH P, GOLBAHAR HAGHIGHI M R, ATASHI M M.Free vibration analysis of elastically supported functionally graded annular plates subjected to thermal environment[J].Meccanica, 2011, 46:893-913.

[10] YANG J, SHEN H S.Non-linear analysis of functionally graded plates under transverse and in-plane loads[J].International Journal of Non-Linear Mechanics, 2003, 38(4): 467-482.

[11] SHEN H S, WANG Z X.Assessment of Voigt and Mori-Tanaka models for vibration analysis of functionally graded plates [J].Composite Structures, 2012, 94: 2197-2208.

[12] SHEN H S, ASCE M, WANG H.Postbuckling of FGM Cylindrical panels resting on elastic foundations subjected to axial compression under heat conduction[J].Journal of Aerospace Engineering, 2015, 28(4): 04014104-1-04014104-15 .

[13] TOULOUKIAN Y S.Thermophysical properties of high temperature solid materials[M].New York: MacMillan, 1967.

[14] LIEW K M, HAN J B, XIAO Z M.Vibration analysis of circular Mindlin plates using the differential quadrature method[J].Journal of Sound and Vibration, 1997, 205(5): 617-630.

[15] IRIE T, YAMADA G, TAKAGI K.Natural frequencies of thick annular plates[J].Journal of Applied of Mechanics, 1982, 49(3) :633-638.

[16] PRADHAN K K, CHAKRAVERTY S.Free vibration of functionally graded thin elliptic plates with various edge supports[J].Structural Engineering and Mechanics, 2015, 53(2): 337-354.

[17] 李清祿,張靖華,李世榮.FGM中厚圓板軸對稱自由振動的打靶法求解[J].振動與沖擊, 2016, 35(18): 95-100.

LI Qinglu, ZHANG Jinghua, LI Shirong.Numerical solution of the Free vibration of functionally graded material moderately thick circular plates by shooting method[J].Journal of Vibration and Shock, 2016, 35(18): 95-100.