基于西門子840D數控系統(tǒng)的龍門五軸數控機床幾何誤差補償軟件開發(fā)*

周顯峰 李 杰 劉辛軍 陳俊宇

(①成都飛機工業(yè)(集團)有限責任公司，四川 成都 610092；②清華大學機械工程系制造工程研究所，精密超精密制造裝備及控制北京市重點實驗室，北京 100084；③北京大學力學與工程科學系，北京 100871)

五軸數控機床因位姿調節(jié)能力強，切削效率高，工件安裝時間短等優(yōu)點逐漸成為復雜工件加工的主要設備。由于復雜的機械結構和控制系統(tǒng)，五軸數控機床空間定位精度相比于三軸數控機床更難得到保證，工零件加工過程中尺寸超差時有發(fā)生[1]。特別是大型龍門五軸數控機床，其加工行程長，龍門跨度大，運動單元重，空間定位精度易超差，周期性誤差補償必不可少。為應對這一問題，眾多機床誤差建模和辨識方法被相繼提出，五軸數控機床加工精度的改善成為當下研究熱點[2]。幾何誤差是影響機床加工精度的主要因素之一[3]，包括定位誤差，直線度誤差，顛擺、偏擺、滾擺誤差及垂直度誤差。在04專項支持下，筆者近幾年系統(tǒng)性地開展了龍門五軸數控機床幾何誤差檢測、辨識和補償方法研究。針對平動軸，提出了十三線幾何誤差辨識方法[4]，利用長方體空間的9條棱、3條面對角線和1條體對角線定位誤差可有效計算出平動軸各項幾何誤差[5]；針對A、C擺動軸，提出了基于偏置球心R-test的幾何誤差辨識方法[6]，通過變更R-test偏置參數獲得關于檢測球頭的多組空間位置誤差，結合誤差模型求解超靜定方程組可辨識轉動軸各項幾何誤差[7]。

在獲得幾何誤差值的基礎上，使用數控系統(tǒng)誤差補償列表對機床誤差進行修正是減小機床空間定位誤差的最有效方法之一[8]。許多知名數控系統(tǒng)廠家均在其推出的數控系統(tǒng)中支持這種補償方法。如Fanuc 30i和Siemens 840D 誤差補償系統(tǒng)，采用激光干涉儀作為檢測設備，在機床工作空間內采集測量數據，然后生成數控系統(tǒng)的誤差補償文件可實現機床幾何誤差的補償[9]。雖然激光干涉儀的檢測值可以直接用于定位誤差補償，但實際測量過程中直接檢測是無法準確獲得平動軸的全部幾何誤差項的(如直接測量的定位誤差實際上是軸間垂直度誤差、角度誤差與實際定位誤差的疊加)。開展機床幾何誤差建模，通過辨識算法求解進給軸全項幾何誤差，更有利于分離干擾誤差項，實現機床幾何誤差的準確補償。筆者經多年研究在龍門五軸數控機床幾何誤差建模、檢測、辨識和補償方面取得了一些研究成果[1-7,10,11]，已經實現根據所提出的辨識算法獲取機床的各項幾何誤差，然后通過數控系統(tǒng)誤差補償列表進行誤差補償。然而，目前誤差補償還只能以手工錄入補償數據的方法來完成，大大限制了補償效率以及研究成果的普及。

機床空間誤差補償技術屬于商業(yè)機密，國外研究機構和機床廠商鮮有文章介紹相關軟件的開發(fā)，而國內基于數控系統(tǒng)的空間誤差補償軟件尚有待開發(fā)。雖然國外已有成熟的VCS(volumetric error compensation system)軟件及配套設備，但其采購和維護費高昂。若全面采用進口儀器和軟件來完成機床的幾何誤差補償，雖然能夠解決一時之急，但長期持續(xù)成本過大而且易受國外技術牽制，同時還制約了我國自主知識產權誤差補償技術的研發(fā)。因此，研制一款具有檢測數據導入、誤差自動辨識、補償文件自動生成和識別功能的幾何誤差補償軟件，對于機床幾何誤差補償方法的應用推廣具有極為重要的工程意義。本文基于筆者所提出的平動軸與擺動軸誤差辨識算法[4,6]，開發(fā)了一種針對Siemens 840D數控系統(tǒng)的幾何誤差補償軟件，通過導入激光干涉儀和R-test的誤差檢測數據[4-7,10-11]能夠自動辨識機床的各項幾何誤差，并將辨識結果以Siemens 840D系統(tǒng)識別的補償格式輸出，從而通過數控系統(tǒng)裝載補償文件實現了幾何誤差自動補償。本文首先闡述了軟件的設計思路及開發(fā)環(huán)境，然后介紹了軟件內部集成的辨識算法及配套檢測策略，在此基礎上介紹了軟件的主要界面及操作流程，最后通過切削S試件驗證了誤差補償軟件的應用效果。

1 軟件設計

功能需求、軟件架構和開發(fā)環(huán)境是軟件設計的三要素。根據現場應用需求調研，立足于簡潔、實用的原則，本章將從功能需求分析、基本架構設計和開發(fā)環(huán)境3個方面介紹該誤差補償軟件的總體設計思路。

1.1 功能分析

軟件開發(fā)的主要目的在于實現測量數據導入、補償數據計算、補償文件生成這3個主要功能，在此基礎上補充一些便于操作的輔助功能。通過對數控廠應用需求的調研，該幾何誤差補償軟件需要實現的主要功能如下：

(1)賬號密碼登陸；(2)機床及軸種類選擇；(3)測量數據導入和刪除；(4)測量數據圖表展示；(5)計算參數導入；(6)補償數據計算；(7)計算結果圖表展示；(8)補償系數導入；(9)補償文件生成。

1.2 基本結構

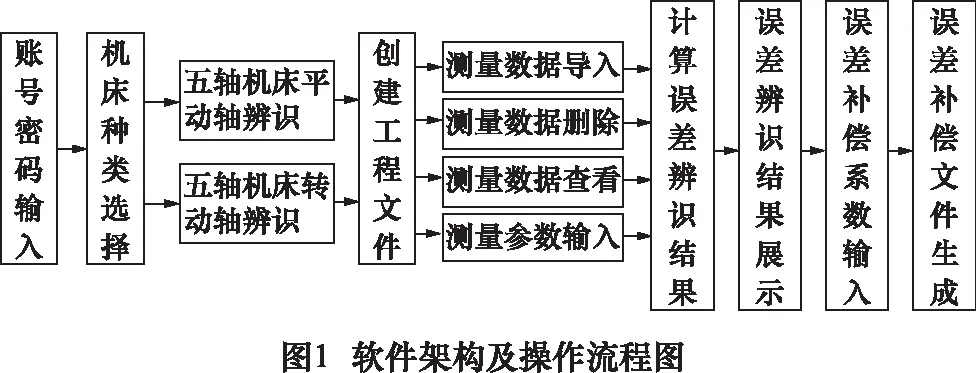
基于功能需求和使用便捷性，規(guī)劃軟件結構及操作流程如圖1所示。首先通過賬號和密碼進入誤差補償軟件，根據需求選擇不同類型的機床(目前只有龍門五軸數控機床，其他為留用接口)。進入機床類型后，根據需要選擇平動軸或轉動軸進行誤差辨識，并創(chuàng)立相應工程文件。在所創(chuàng)建的工程文件里進行的主要操作包括：測量數據導入(測量數據是在給定檢測策略下獲得[5,7])、數據查看、數據刪除(修改)以及檢測參數輸入。完成數據導入和辨識條件配置后，即可進行幾何誤差辨識計算以及結果的展示。此外，可以根據工程需要通過補償系數對補償數據進行修正，最終由軟件生成西門子數控系統(tǒng)識別的補償文件。

1.3 開發(fā)環(huán)境

本軟件以Windows平臺為基礎，選擇了Qt[12]作為開發(fā)框架，Qt Creator作為開發(fā)環(huán)境，使用C++進行程序語言編寫。選擇C++作為編程語言能實現對數據和合法操作的封裝，有利于在數值分析復雜的數據計算中保持各組數據間不會出現相互干擾。對于32位簡化系統(tǒng)工控機運行環(huán)境，C++具有更好的兼容性。Qt是1991年由奇趣科技開發(fā)的跨平臺C++圖形用戶界面應用程序開發(fā)框架，其良好的封裝性和高模塊化程度使得其各個元件之間的協同工作變得十分簡單，對于開發(fā)需要進行窗口模塊間反復傳值調用的工業(yè)軟件而言有著巨大的優(yōu)勢。同時，大量已經開發(fā)成型的模塊可以被直接用于軟件編寫(如本軟件中繪圖部分采用的qwt[13-15]即為基于LGPL版權協議的開源項目，可生成各種統(tǒng)計圖)，從而能大大加快程序的開發(fā)速度。Qt Creator[16]是與Qt配套的集成開發(fā)環(huán)境，能夠幫助Qt用戶快速地入門、開發(fā)和運行項目。內部集成的Qt Designer能夠方便開發(fā)人員對軟件窗口進行可視化布局，同時其對Qt核心的信號槽機制也有配套的圖示調節(jié)器。

2 核心算法

龍門五軸數控機床幾何誤差補償軟件，包括平動軸幾何誤差辨識、補償模塊和擺動軸幾何誤差辨識、補償模塊兩個重要部分。由于兩種進給軸的拓撲類型不同，所采用的檢測策略和辨識方法都有所差異。幾何誤差檢測方法和辨識算法是本軟件算法的核心所在，本文將分別對平動軸和擺動軸的測量方法和辨識算法進行簡要說明。

2.1 平動軸幾何誤差辨識

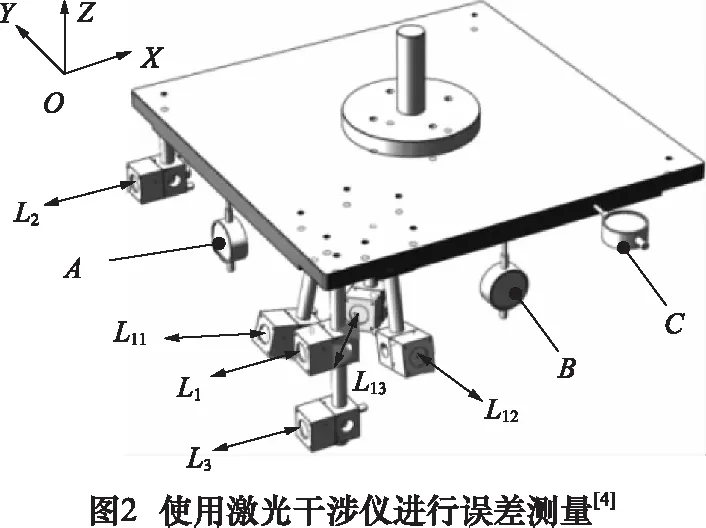
平動軸幾何誤差辨識以激光干涉儀為檢測工具，通過輔助工裝將反射鏡與機床主軸固連。如圖2為輔助工裝三維圖，雙箭頭L1～L13表示檢測軌跡，對應軌跡上安裝有激光干涉儀反射鏡，輔助工裝通過圓軸安裝在機床主軸上[10]。根據檢測策略[5]編寫數控代碼，驅動機床運動使反射鏡沿檢測軌跡移動，通過激光干涉儀檢測給定軌跡上的定位誤差[10]。測量所得定位誤差以rtl后綴文件形式保存，如圖3所示為激光干涉儀檢測文件的格式。本軟件將對激光干涉儀檢測文件進行自動識別，將測量值取至數組中用于進行后續(xù)計算。

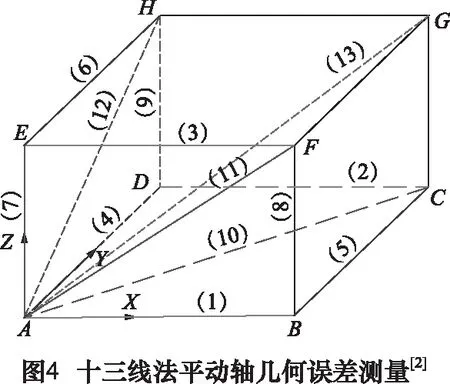
平動軸幾何誤差檢測所測得定位誤差實質上是機床各項幾何誤差綜合作用的結果。為從定位誤差檢測結果中辨識出各項幾何誤差，軟件采用筆者所提出的十三線辨識方法[4](檢測軌跡如圖4所示)，以長方體空間的9條棱，3條面對角線與1條體對角線的各檢測點上定位誤差為數據源。通過X、Y、Z軸運動矩陣和誤差傳遞矩陣構建刀具幾何誤差模型，在給定檢測軌跡下得到幾何誤差辨識方程，并通過逐步分離和最小二乘法解算各項幾何誤差[5]。

2.2 轉動軸幾何誤差辨識

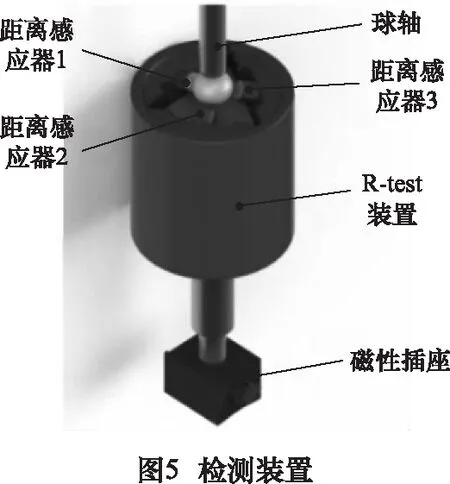
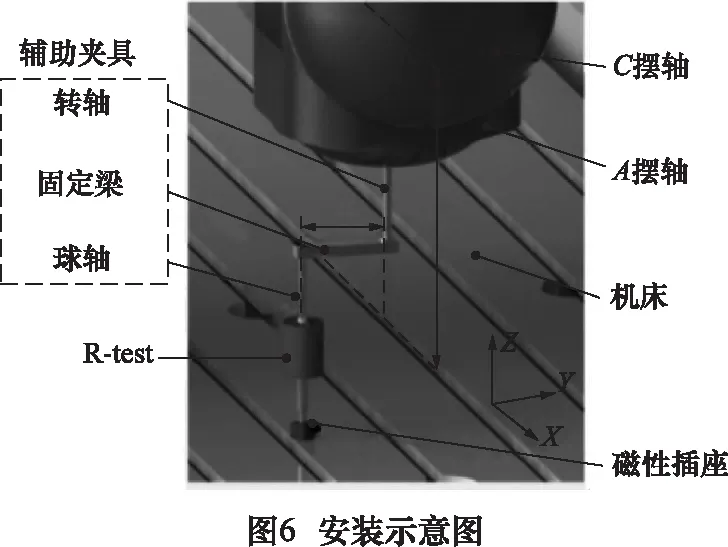
擺動軸幾何誤差辨識以R-test作為檢測工具，通過輔助工裝將帶有偏置的球形檢測頭安裝于機床主軸上[11]。基于數控機床RTCP運動功能，通過3個非接觸式位移傳感器檢測在不同擺角時球頭相對于空間理想位置的三維誤差[2]。如圖4所示為R-test檢測示意圖[6]，圖6所示為R-test檢測所得數據的格式。在C擺動軸誤差檢測時，讓A擺動軸靜止，通過輔助工裝3次改變球頭相對于機床主軸的偏置參數(圖6所示的水平偏置H和豎直參數L)，進行RTCP運動檢測得到3組數據[7]。將檢測數據和A擺動軸幾何誤差模型[6]結合建立A擺動軸幾何誤差辨識模型，利用最小二乘法求解超靜方程組得到A擺動軸各項幾何誤差[7]。在A擺動軸幾何誤差檢測時，讓C擺動軸保持靜止，然后以類似的方式改變偏置參數，進行3次RTCP運動誤差檢測。最終將A軸的誤差檢測數據和幾何誤差模型結合，即可辨識出A軸在各個擺角下的幾何誤差。

3 操作流程及界面說明

根據前2章所介紹的程序架構和辨識算法，即可應用C語言在QT框架下編寫補償軟件的人機交互界面。本章將對軟件的誤差辨識操作流程和主要界面進行介紹。

3.1 軟件主界面

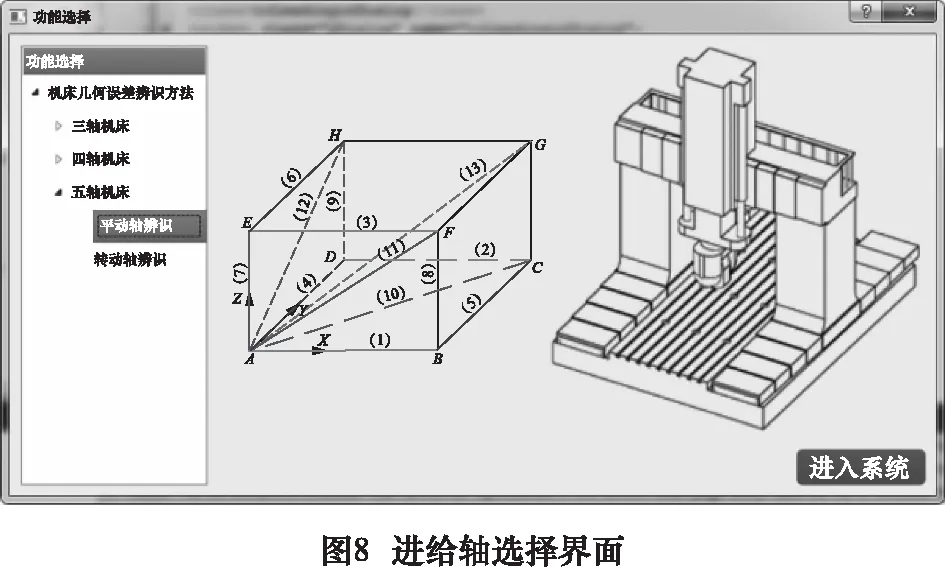
圖7所示為軟件登陸界面，輸入用戶名和密碼點擊登陸按鈕即可進入軟件主界面。對于不同種類的數控機床以及不同拓撲結構的進給軸，誤差檢測策略和辨識方法存在很大差異，數據處理方法和輸出格式也有所不同。本文主要介紹龍門五軸數控機床平動軸和擺動軸幾何誤差辨識與補償，其他類型機床可在后期研究工作完成后作為擴展目標添加到該軟件。圖8所示為龍門五軸數控機床進給軸選擇界面，可以根據辨識需求進入相應界面。

3.2 平動軸檢測數據導入與誤差辨識

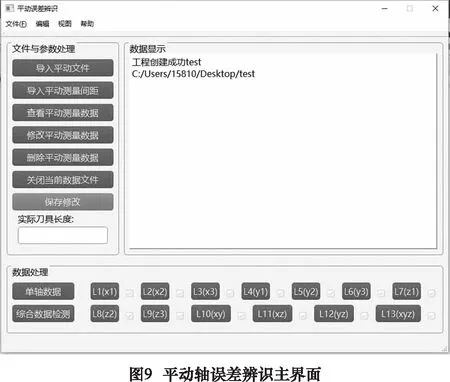
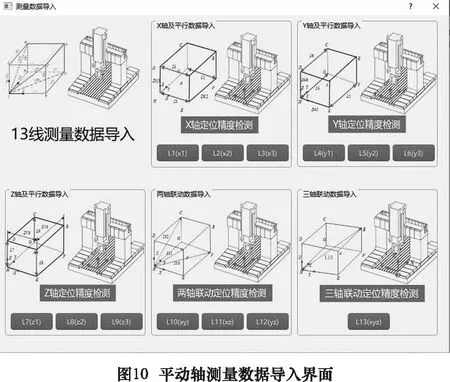
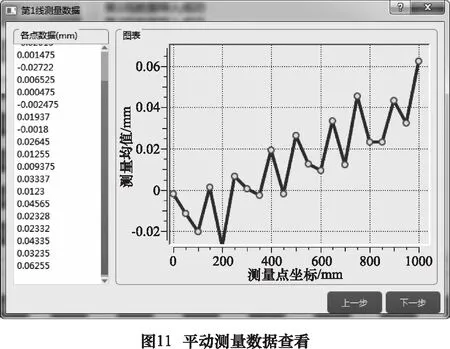
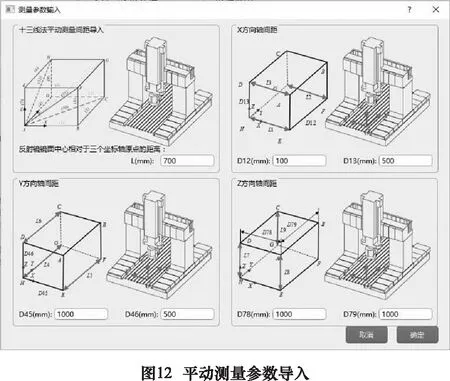
點擊圖8中平動軸辨識按鈕，進入平動軸誤差辨識主界面，如圖9所示。點擊界面左上角文件按鈕，選擇新建文件或者打開文件后，可新建辨識工程或打開已有辨識工程進行操作。平動軸幾何誤差辨識程序是基于13線法開發(fā)的，點擊“導入平動文件”按鈕可將13組測量數據分別導入辨識程序，導入界面如圖10所示。已經導入的數據會在對應線號旁以綠鉤形式提示，點擊線號按鈕可查看已經導入的各組數據，數據查看界面如圖11所示。如果有存在疑問的數據可以刪除后重新導入或對局部數據進行修正。完成檢測數據導入后，點擊“導入平動測量間距”按鈕輸入測量工裝的參數(圖12)，即可為誤差辨識提供計算參數。

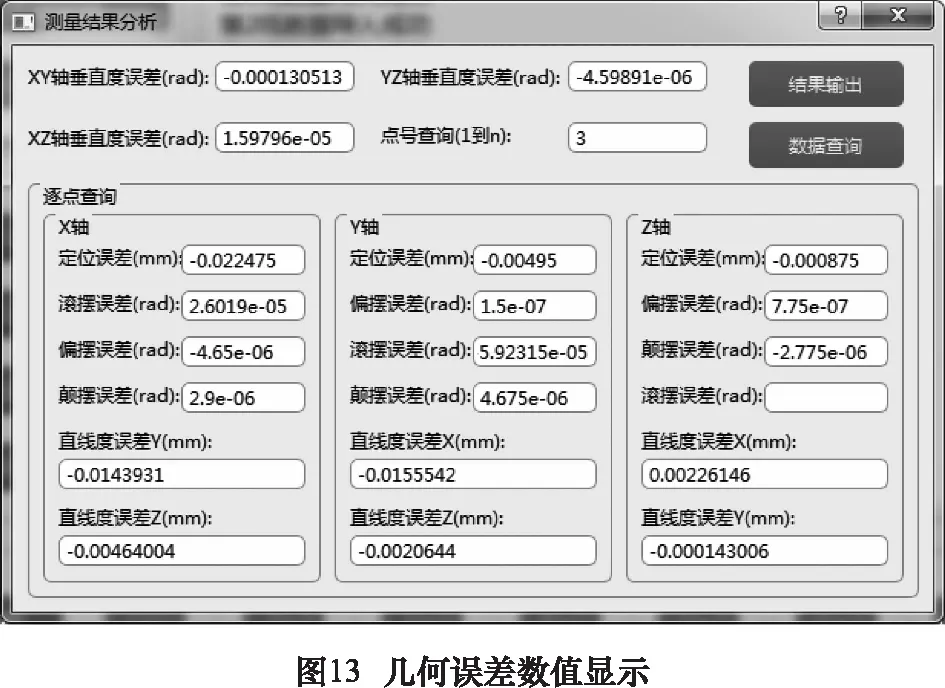
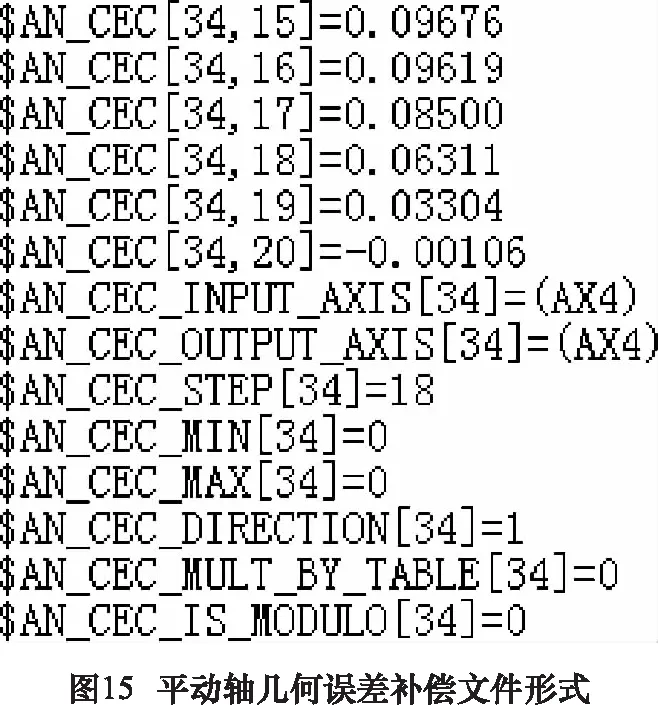
在測量數據和測量參數都導入之后，點擊主界面(圖9)的“綜合數據檢測”按鈕即可在新的窗口中查看誤差辨識結果，如圖13為幾何誤差辨識結果顯示界面。輸入查詢點號后點擊數據查詢按鈕，窗體下方即顯示X、Y、Z三軸上相應點的各項誤差值。點擊“結果輸出按鈕”可在新的窗口中對誤差補償輸出值進行定義和修正。根據實際誤差檢測情況定義檢測零點在機床坐標系下的坐標值，從而確定補償列表生成的起始點。在補償修正系數窗口更改各項補償值的修正倍率(初始為1)，有助于實現迭代補償，提升補償效果。在補償修正系數和檢測坐標確定之后，點擊“保存并繪圖”按鈕即可將補償數據以圖形展示(如圖14所示)。點擊“輸出至文件”按鈕，補償文件會自動生成至初始創(chuàng)建工程的文件夾中，該補償文件形式如圖15所示，可以直接導入數控系統(tǒng)實現平動軸幾何誤差自動補償。

3.3 擺動軸檢測數據導入與誤差辨識

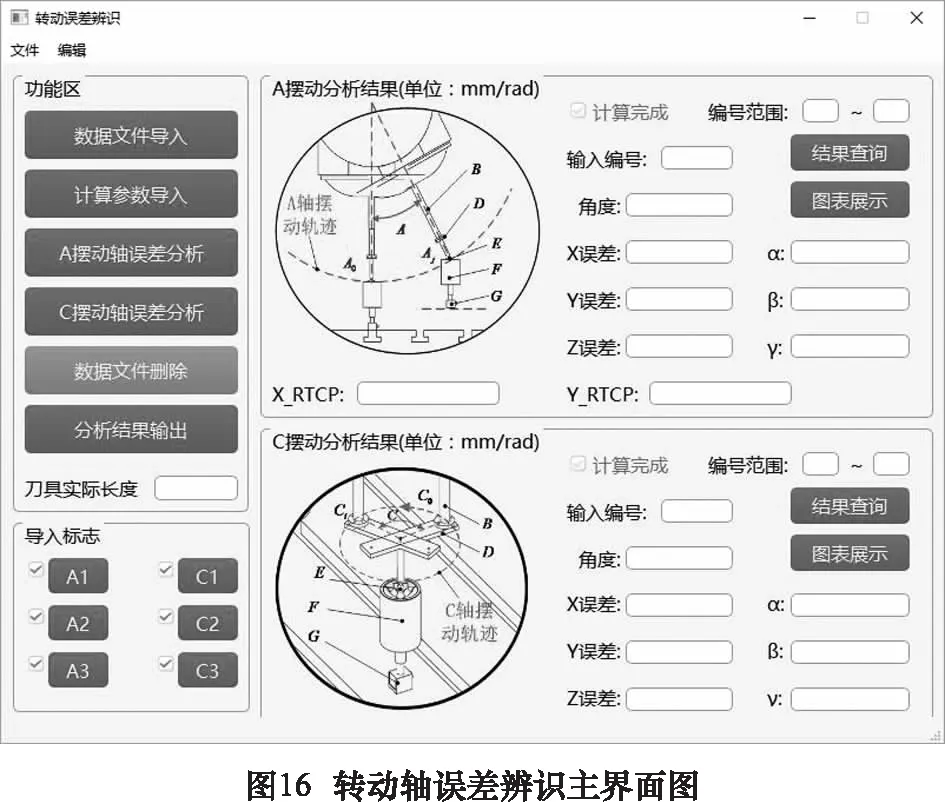
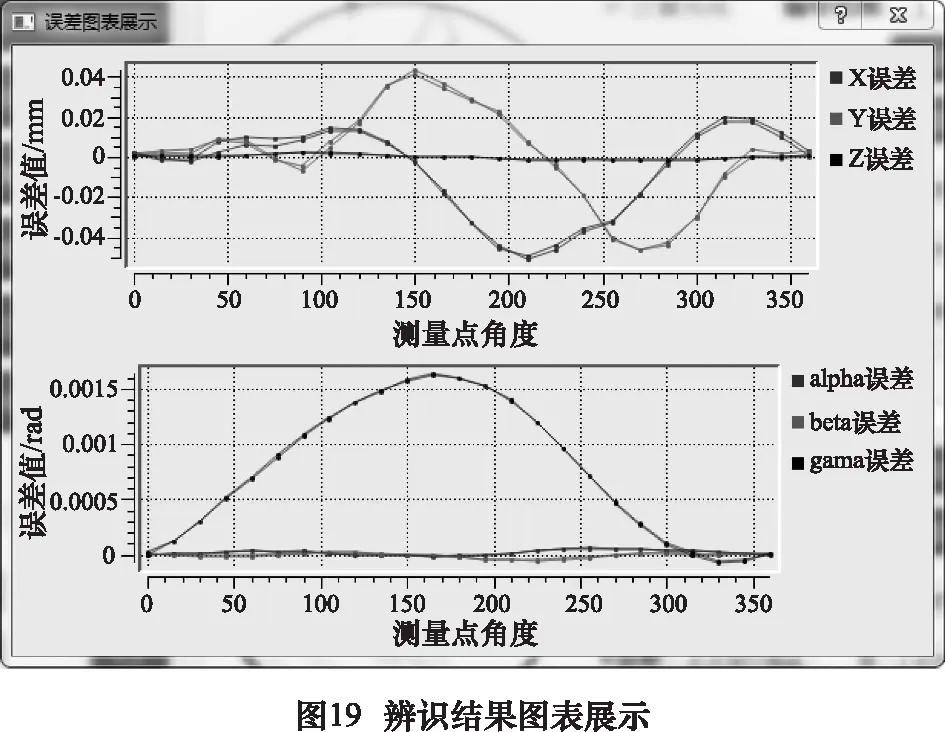
在進給軸選擇界面(圖8所示)選擇“轉動軸辨識”進入轉動軸辨識程序。點擊界面左上角文件按鈕，選擇新建文件或者打開文件后，即可在打開工程中進行后續(xù)操作。基于轉動軸幾何誤差檢測策略[7]，在轉動軸誤差辨識主界面(如圖16所示)的引導下，分別將A、C擺動軸所對應的3組數據導入軟件。已經導入的數據會在下方以綠鉤加以提示，可點擊相應按鈕查看已經導入的各組數據(如圖17所示)，如果有存在疑問的數據可以刪除后重新導入或對局部數據進行修正。接著可以在“計算參數導入”下輸入工裝的偏置參數，具體輸入形式與圖12所示平動測量參數導入類似。A擺動軸和C擺動軸的辨識算法互相獨立，故點擊左側的“A/C擺動軸誤差分析”可以分別獲得其誤差辨識結果。計算完成后，右側“計算完成”按鈕旁會顯示綠鉤，輸入查詢編號后點擊“結果查詢按鈕”即可查看相應角度的各項誤差(如圖18所示)。當擺動軸誤差計算完成后，點擊相應圖表展示按鈕，即可在新窗口中以曲線圖的形式查看辨識結果(如圖19所示)。

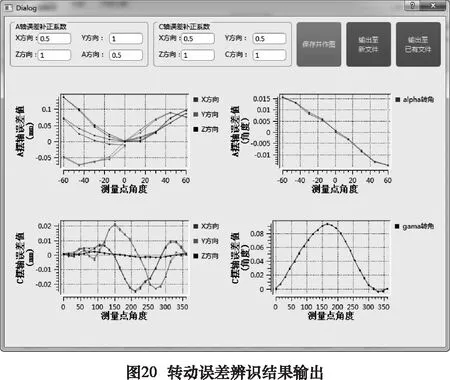
在完成擺動軸幾何誤差辨識計算后，點擊主界面上的“分析結果輸出”按鈕，在彈出窗口中輸入各個補償值的修正系數，點擊“保存并作圖”即可圖形化顯示補償數據的基本情況，如圖20所示。在圖20中核對數據無誤后，點擊輸出至新文件即可在工程文件夾中生成補償文件(該數據只補償了擺動軸)，或者點擊輸出至已有文件后選擇平動軸辨識中生成的補償文件，轉動軸的補償值會被追加在平動軸補償文件的末尾(該數據對平動軸和擺動軸同時進行了補償)。

4 軟件補償效果驗證

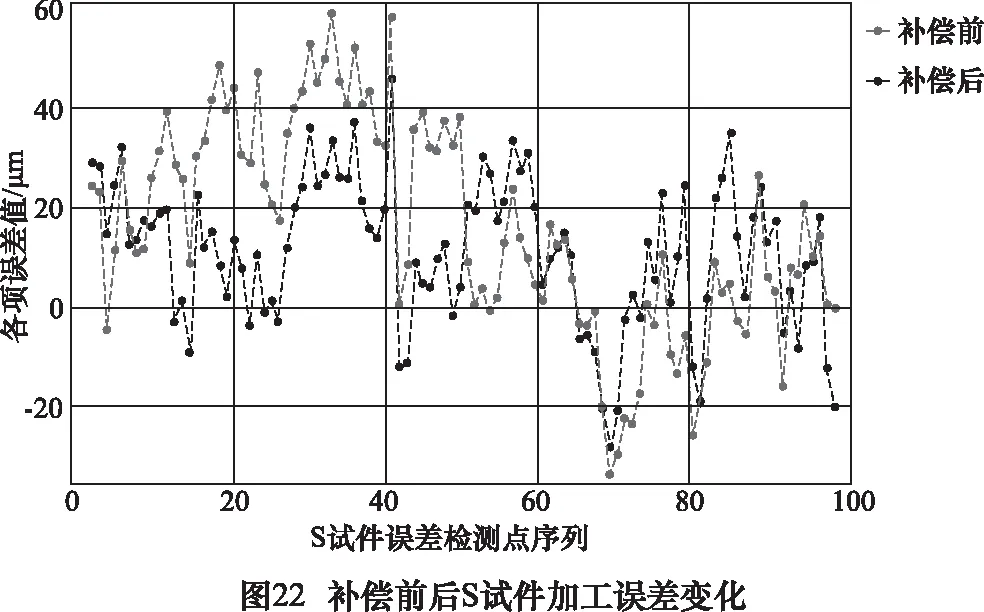
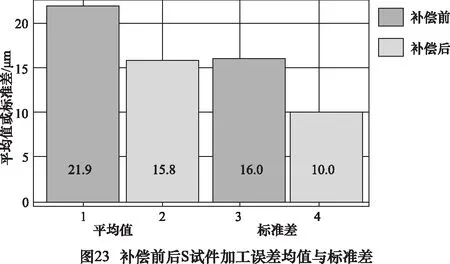
為驗證幾何誤差補償軟件的實用性，如圖21所示，在一臺龍門五軸數控機床上進行了 S試件切削實驗。采用對比補償前后機床切削S試件的加工精度對機床的加工精度進行了評估和比較。為了反映加工誤差的大小，在S試件曲面上選擇了100個特征點，分別測量其在曲面法向上的加工誤差值。在無誤差補償的情況下進行一次S試件加工與誤差測量，然后基于誤差檢測數據利用誤差補償軟件導入誤差補償文件再進行一次加工。將兩次試件的加工誤差進行對比，誤差補償前后加工誤差的變化如圖22所示，補償前后S試件加工誤差平均值與方差如圖23所示。

由圖22可知，S試件100項檢測誤差中補償前最大值為59.7 μm補償后最大值減小至46.3 μm，最大誤差改善效果達到了22.4%。同時由圖23可知，補償后100項誤差均值從21.9 μm減小至16 μm，平均改善效果改善了26.9%，標準差從15.8 μm減小至10 μm，加工精度穩(wěn)定性提升了36.7%。由此說明，采用該軟件對機床幾何誤差進行補償后，機床的加工精度和加工穩(wěn)定性都有較為明顯的提升。

5 結語

本文以具有西門子840D數控系統(tǒng)的龍門五軸數控機床為應用對象，基于十三線平動軸幾何誤差辨識方法和偏置球心R-test的擺動軸幾何誤差辨識方法，在C++環(huán)境下利用QT界面設計框架，開發(fā)了一種幾何誤差補償軟件。軟件在導入激光干涉儀和R-test誤差測量數據后，可以快速辨識出機床各項幾何誤差，并輸出能被西門子數控系統(tǒng)識別的補償文件，通過數控系統(tǒng)加載補償文件便可以實現幾何誤差的自動化補償，有效地提升了數控機床幾何誤差補償的效率。通過切削S試件對軟件誤差應用效果進行了驗證，結果表明應用該軟件進行誤差補償可以有效提升機床在加工精度和加工穩(wěn)定性。本文所開發(fā)的誤差補償軟件可以快速、高效地實現龍門五軸數控機床幾何誤差的補償，為機床航空結構件加工精度的保證提供了有力支持。此外值得指出，以現有單機版本軟件為基礎，在辨識算法優(yōu)化、人機交互、操作便捷性方面繼續(xù)深入挖掘，基于網絡架構開發(fā)出更為通用的誤差補償軟件，在航空結構件加工領域乃至整個機械加工領域都有重大的應用前景。

[1]李杰, 劉辛軍, 謝福貴,等. 基于時變特性的數控機床綜合誤差建模方法[J]. 科技導報, 2016, 34(2):65-70.

[2]李杰, 謝福貴, 劉辛軍,等. 五軸數控機床空間定位精度改善方法研究現狀分析[J]. 機械工程學報,2017，53(7):113-128.

[3]Li J, Xie F, Liu X J. Geometric error modeling and sensitivity analysis of a five-axis machine tool[J]. The International Journal of Advanced Manufacturing Technology, 2016, 82(9):2037-2051.

[4]Li J, Xie F, Liu X J, et al. Geometric error identification and compensation of linear axes based on a novel 13-line method[J]. International Journal of Advanced Manufacturing Technology, 2016, 87(5-8): 2269-2283.

[5]劉辛軍, 李杰, 董澤園,等. 機床平動軸幾何誤差辨識方法, CN105538038A[P]. 2016.

[6]Li J, Xie F, Liu X J, et al. A geometric error identification method for the swiveling axes of five-axis machine tools by static R-test[J]. International Journal of Advanced Manufacturing Technology, 2017, 89(9):3393-3405.

[7]劉辛軍, 李杰, 陳俊宇,等. 基于RTCP的五軸數控機床擺動軸幾何誤差辨識方法, CN105479268A[P]. 2016.

[8]Dave Maxham.空間誤差補償技術在大型多軸機床標定中的實用方法[J]. 航空制造技術, 2010(13):46-49.

[9]周漢輝. 數控機床三維幾何誤差補償技術的應用[J]. 航空制造技術, 2011(6):40-43.

[10]劉辛軍, 李杰, 朱紹維，等. 一種激光干涉儀輔助組合夾具, CN104729401A[P]. 2015-06-24.

[11]劉辛軍, 李杰, 董澤園. 用于雙擺頭五軸數控機床R-test檢測的輔助工裝, CN 106041643A[P]. 2016

[12]Qt, Nokia Corporation. QtCross-platform application and UI framework, 4.8.2[EB/OL]. 2012. .

[13]Uwe Rathmann Josef Wilgen. Qwt User's Guide[M].2008

[14]Rathmann, U, Wilgen, J. Qwt-Qt Widgets for Technical Applications, 6.0.1[EB/OL].2012. .

[15]盧華偉, 秦品健, 鄭銳. 基于Qt/Qwt的操作監(jiān)控系統(tǒng)的設計與實現[J]. 微計算機信息, 2010, 26(1):72-74.

[16]霍亞飛. Qt Creator快速入門[M].北京：北京航空航天大學出版社, 2014.