基于水冷壁壁溫的爐膛火焰中心位置預測方法
陳有福, 徐頌梅, 管詩駢, 丁建良, 姚旭東, 趙伶玲
(1. 江蘇方天電力技術有限公司, 南京 211102; 2. 東南大學 能源與環(huán)境學院, 南京 210096)
鍋爐爐膛的火焰中心是體現鍋爐燃燒狀況的重要因素,是爐內燃燒狀態(tài)的直接反映。火焰中心如果發(fā)生偏斜,不僅影響爐膛內煙氣溫度場及流場分布,還會影響受熱面的磨損、結渣以及吸熱量的分配等,嚴重時會導致爐內受熱面的傳熱惡化、水冷壁和屏式受熱面的超溫爆管。因此,及時有效地監(jiān)測火焰中心是否偏斜,為運行人員提供預警和參考,具有一定的理論與實際應用價值。
當前關于火焰中心位置的研究一般是通過溫度場模擬、火焰光譜信息處理等[1-3];但實際鍋爐巨大的爐膛空間使得火焰中心難以測量,在鍋爐上安裝大量測點又耗資巨大,施工困難。因此,如能利用鍋爐現有測點,簡單有效地預測火焰中心是否偏斜,將大幅度地節(jié)約成本,提高鍋爐運行的安全性和經濟性。
為了提高預測準確度,同時減小預測過程的復雜度,筆者提出了一種基于鍋爐水冷壁壁溫的爐膛火焰中心位置預測方法,并以某600 MW電站鍋爐為例,驗證預測方法的可行性和準確性。
1 預測思路
鍋爐爐膛內熱量交換主要是高溫煙氣對水冷壁的輻射傳熱。當爐膛火焰中心未發(fā)生偏移,以四角切圓鍋爐為例,由于鍋爐橫截面為近似的正方形,所以四面墻的水冷壁接受爐內高溫煙氣輻射的傳熱量應近似相等,其各面墻水冷壁的壁溫分布也應近似相同[4]。若火焰中心發(fā)生偏斜,高溫煙氣對四面墻水冷壁的輻射傳熱量發(fā)生了改變,水冷壁壁溫會產生規(guī)律性的變化,即靠近火焰中心的水冷壁壁溫將整體升高,遠離火焰中心的水冷壁壁溫將整體降低。
筆者提出了一種基于四角切圓鍋爐下部水冷壁(垂直型)已有溫度測點的爐膛火焰中心位置預測方法,將爐膛火焰中心位置預測分為兩個部分:第一部分建立爐膛火焰中心位置與水冷壁壁溫分布計算模型及數據庫,第二部分利用第一部分所建模型和數據庫進行爐膛火焰中心位置的判定。具體流程圖見圖1。

圖1 爐膛火焰中心位置預測方法流程圖
2 熱負荷分布與壁溫分布數據庫
2.1 爐膛計算區(qū)域劃分
為便于計算,將爐膛沿高度和寬度方向分區(qū),沿高度方向分為20個計算區(qū)域,沿寬度和深度方向分為10 × 10的計算區(qū)域,見圖2。圖2中還給出了爐膛燃燒器的布置區(qū)域和燃盡風位置情況,爐墻上的實心點(右邊)為鍋爐水冷壁壁溫熱電偶的布置位置。
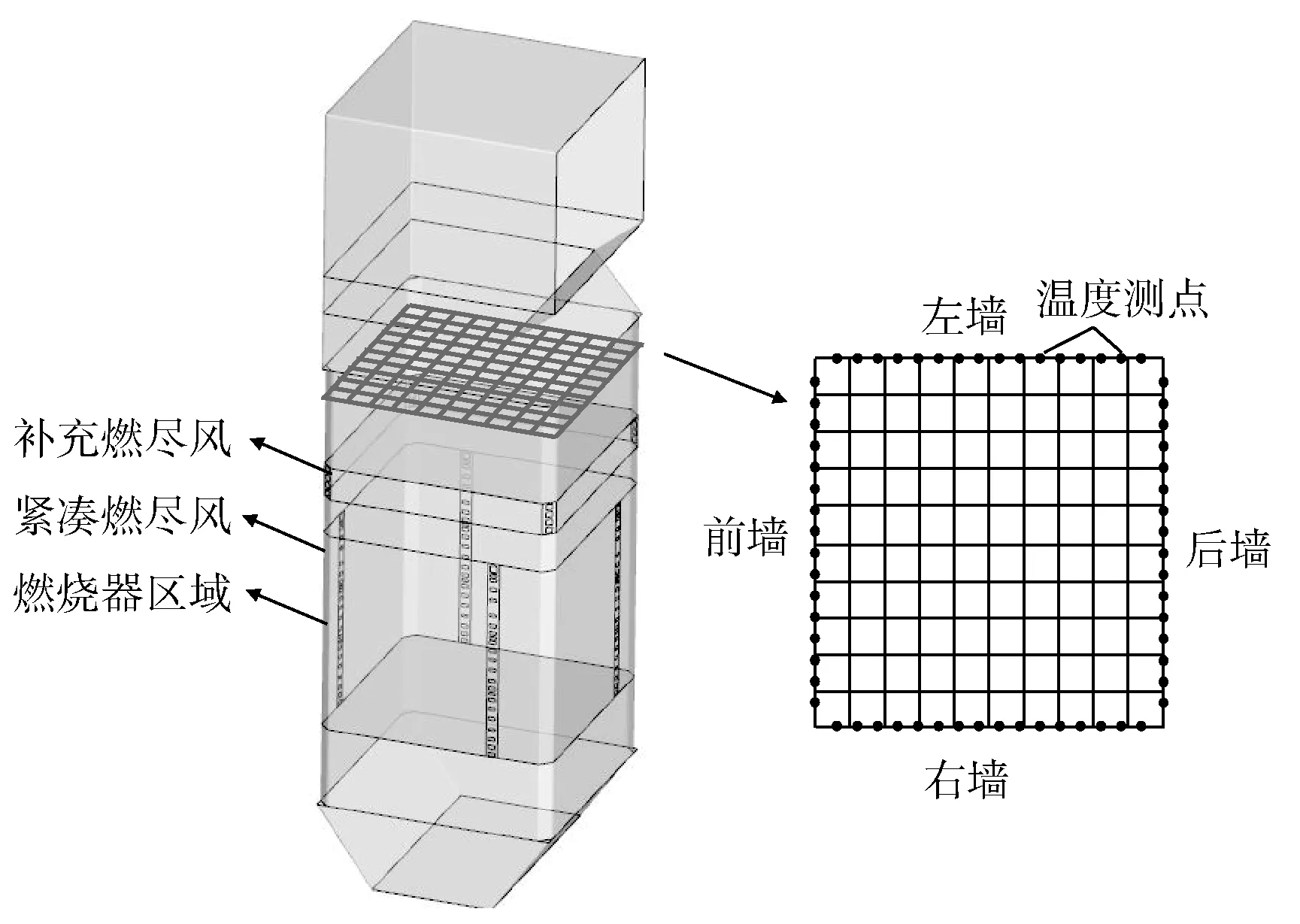
圖2 爐膛計算區(qū)域劃分及測點位置示意圖
2.2 計算模型
水冷壁管壁溫度按下式計算:
(1)
式中:tcr為計算出的水冷壁管壁溫度,℃;t為水冷壁管計算截面上流動介質的平均溫度,℃;Δt為水冷壁管內工質溫度大于該截面平均溫度的值,K;β為管子外徑與內徑的比值;μ為熱散漫系數;q為水冷壁管外表面的熱負荷,kW/m2;δ為管子壁厚,m;λm為水冷壁管的導熱系數,kJ/(m·s·K);α為管壁向被加熱介質的放熱系數,kJ/(m2·s·K)。
其中,每一計算區(qū)域的熱負荷為:
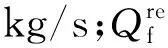
故水冷壁壁面熱負荷可通過水冷壁壁面的熱負荷不均勻系數計算得到。其中,ηa、ηb的取值隨著爐內火焰中心位置的改變而變化。由此可見,爐膛熱負荷與爐膛火焰中心位置是相互關聯(lián)的,故可建立爐膛熱負荷與爐膛火焰中心位置的預測模型。
計算所選用的沿爐膛高度和寬度方向熱負荷不均勻系數[4]見圖3。爐膛出口區(qū)域的相對高度為0.9~1.0,燃燒器區(qū)域為0.2~0.55,其余部分為爐墻水冷壁。


圖3 熱負荷不均勻系數
爐膛相對高度x、相對寬度y處區(qū)域水冷壁工質焓值為:
(2)
式中:qy為在爐膛相對高度x、相對寬度y處區(qū)域的熱負荷,kW/m2;qx為爐膛相對高度x處的平均熱負荷, kW/m2;Δi為工質相對高度x處的平均焓增,kJ/kg;ix-1為工質在計算高度x-1下的平均焓值,kJ/kg。
通過鍋爐爐膛熱力計算可得到整個爐膛的平均熱負荷,之后編制水冷壁壁溫與火焰中心位置關系的計算程序。
2.3 數據庫建立
將鍋爐不同負荷、一次風量和風溫、二次風量和風溫下爐膛熱負荷分布與水冷壁壁溫分布相對應,并存入數據庫中。通過預計算得到工況分布下的熱負荷分布與水冷壁壁溫分布一一對應的數據,形成完整的數據庫。
3 算例分析
3.1 研究對象
筆者以HG-1792/26.15-YM型600 MW機組鍋爐為例進行模型建立與分析。該鍋爐采用П形布置、單爐膛、改進型NOx主燃燒器和MACT型低NOx分級送風燃燒系統(tǒng)、墻式切圓燃燒方式。鍋爐燃用的煤種為芙蓉貧煤,采用中速磨正壓直吹式系統(tǒng),每爐配6臺磨煤機。計算工況為75%最大連續(xù)蒸發(fā)量(BMCR),該負荷4臺磨煤機運行,燃燒器開4層,并在燃燒器上部布置燃盡風。表1給出了該工況下的主要參數。
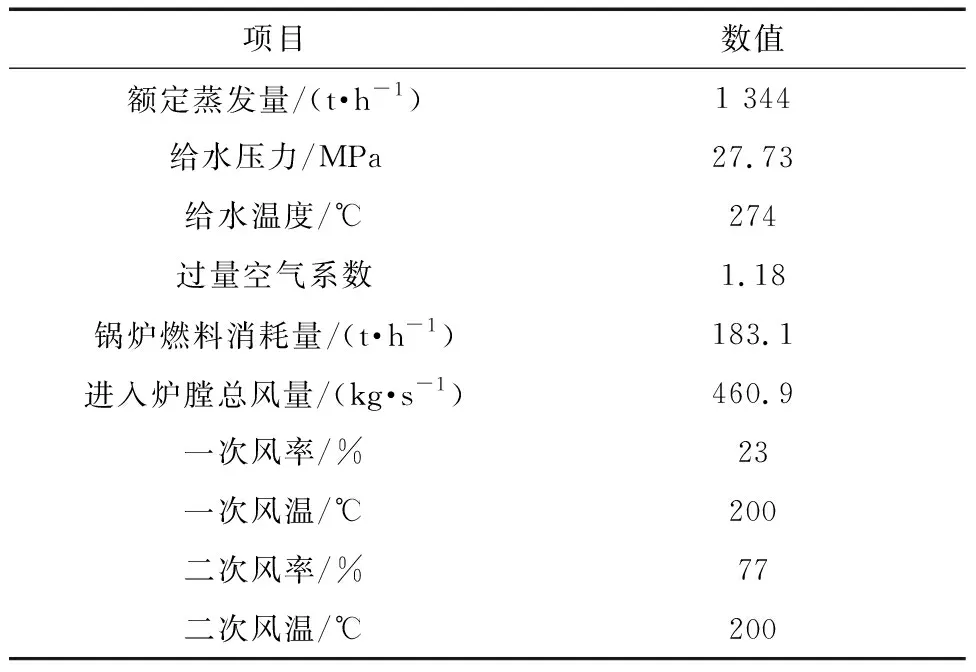
表1 75%BMCR工況參數
爐膛水冷壁采用焊接膜式壁、內螺紋管垂直上升式,爐膛斷面尺寸為17.666 m×17.628 m,水冷壁管共有1 584根,前后及兩側墻各396根,均為管徑為28.6 mm、最小壁厚為6.4 mm的四頭螺紋管,在上下爐膛之間裝設了一圈中間混合集箱,以消除下爐膛工質吸熱與溫度的偏差。
在下部水冷壁出口,即進入過渡聯(lián)箱處,沿爐膛橫截面四周裝有64個熱電偶測量水冷壁管壁溫度,每面爐墻均勻布置了16個。
3.2 計算模型驗證
首先由火焰中心未偏移工況對該計算模型進行驗證,將整個爐膛區(qū)域視作一個二維的壁面,水冷壁壁溫沿爐膛高度與寬度方向變化。通過鍋爐爐膛整體的熱力計算得到鍋爐爐膛的平均熱負荷與工質參數,通過熱負荷分配系數可求得爐膛內不同高度與寬度水冷壁熱負荷大小,通過計算所得工質參數與爐膛內不同高度與寬度水冷壁熱負荷大小可求得水冷壁壁溫分布。經數據處理得到的沿爐膛高度方向工質溫度與水冷壁壁溫分布曲線見圖4,通過編制的計算程序,計算所得不同爐膛高度橫截面水冷壁壁溫分布曲線見圖5。
由圖4可以看出:在燃燒器區(qū)域,水冷壁溫度達到最大值,此時工質溫度上升速度也最大。在爐膛中部區(qū)域工質處于大比熱容區(qū)[5-7],溫度上升速度較慢。在爐膛遠離燃燒器區(qū)域位置,由于熱負荷較低,水冷壁壁溫也較低[8]。圖5中選取的三個相對高度截面分別為燃燒器區(qū)域下部(x=0.2)、燃燒器區(qū)域(x=0.6)和爐膛出口(x=0.95)。由于此時計算的是火焰中心在爐膛中心沒有偏移時的工況,因而水冷壁壁溫沿爐膛寬度方向均為對稱分布,在離火焰中心較近處水冷壁壁溫較高,遠離火焰中心處水冷壁壁溫較低。在燃燒器區(qū)域煙溫較高,故該處熱負荷較大,且在火焰中心未偏移的情況下,靠近爐膛中心的煙氣溫度較高,四周溫度較低,此時產生的水冷壁中心區(qū)域和兩側的煙溫偏差較大,故該截面水冷壁壁溫差異也較大,該分布趨勢與實際運行結果相符。
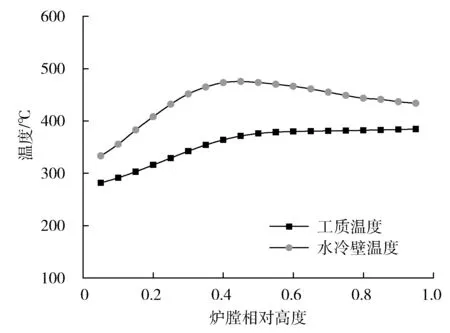
圖4 沿爐膛高度水冷壁溫度與工質溫度

圖5 不同爐膛相對高度水冷壁壁溫
水冷壁壁溫計算值與測量值誤差:
(3)
式中:δ為相對誤差,%;ts為水冷壁壁溫的實測值,℃。
沿爐膛相對高度0.9處水冷壁壁溫計算結果與該處爐膛實際測點數據的對比見圖6。從圖6可以看出:沿爐膛寬度方向,水冷壁壁溫實測值與計算值有一致的變化規(guī)律,呈現出兩側壁溫低、中間壁溫高的特點,但計算值略偏高于實測數據。這是由于在計算管壁溫度時,未考慮水冷壁的污染及灰污熱阻等,因而會帶來一定的誤差。計算值與實測值的相對誤差最大值為6.9%,最小值為3.6%,計算值與實測值具有良好的一致性,計算結果基本可靠。因此,通過此方法計算的水冷壁壁溫分布可作為爐膛火焰中心位置判斷的依據。

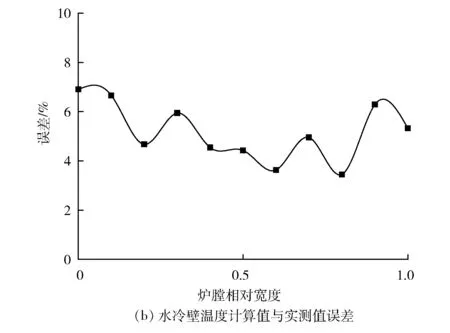
圖6 下部水冷壁出口壁溫計算值與實測值比較及誤差分析
3.3 火焰中心位置預測
筆者對實際運行時存在火焰中心偏斜的情況進行了預測。從監(jiān)控系統(tǒng)中讀出四面墻下部水冷壁出口壁溫的64個測點數據,并根據此時鍋爐負荷、燃煤量、一二次風量,調用所建立的爐膛熱負荷分布與水冷壁壁溫分布數據庫。通過計算得到的火焰中心位置,此時火焰中心向前墻偏移1.7 m。該工況前、后、左、右四面墻的水冷壁壁溫分布曲線和根據所建爐膛熱負荷與爐膛火焰中心位置的預測模型得出的爐膛內火焰中心位置見圖7。
由圖7可知:在火焰中心位置偏移時,水冷壁壁溫會呈規(guī)律性變化,呈現出前墻壁溫升高、后墻壁溫降低,左、右兩側墻壁溫最高溫度點向前墻側偏移的特點[3,9-10]。前墻水冷壁最高溫度由火焰中心未發(fā)生偏移工況下的462 ℃升高至468 ℃,而后墻水冷壁的最高溫度由火焰中心未發(fā)生偏移工況下的462 ℃降低至457 ℃,左、右兩側墻水冷壁最高溫度點分別相對于火焰中心偏移了10%的距離。
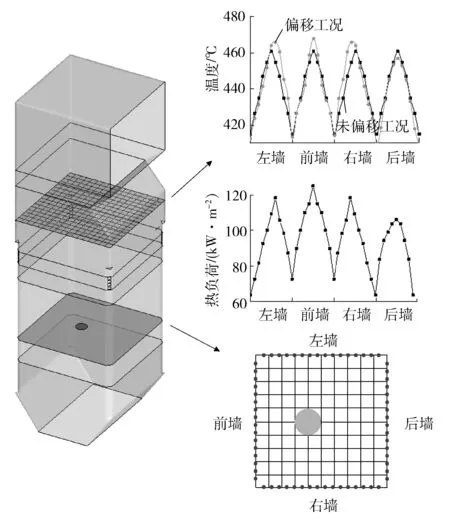
圖7 火焰中心位置偏移示意圖
4 結語
(1) 采用爐膛熱負荷與爐膛火焰中心位置的預測模型能夠較為準確地描述爐膛火焰中心的位置,建立合適的壁溫計算模型有利于提高火焰中心位置預測的精度。
(2) 該預測方法的火焰中心位置預測可靠性較高。通過與實測的數據對比,誤差在允許的范圍內,證明該模型具有一定的準確性。當火焰中心向某一側墻偏移時,該側水冷壁壁溫會整體升高,而對面墻壁溫會整體下降,且變化的幅度與爐膛火焰中心位置的偏移量有關。
(3) 該預測方法僅需利用鍋爐現有溫度測點,即可進行火焰中心位置的判別,不需要另外投資設備與繁雜的測繪工作,預測方法簡單,易于實現。
參考文獻:
[1] 張力, 趙亮宇. 基于證據理論的爐膛火焰中心高度判別[J]. 電站系統(tǒng)工程, 2014, 30(3): 21-23.
[2] 吳琛, 常太華, 田亮, 等. 基于數理統(tǒng)計的爐膛火焰中心高度構造及驗證[J]. 電力科學與工程, 2010, 26(5): 42-46.
[3] 高正陽, 崔偉春, 楊毅櫟, 等. 火焰中心高度對W型火焰鍋爐燃燒影響的數值模擬研究[J]. 熱力發(fā)電, 2009, 38(11): 23-27.
[4] 周強泰, 華永明, 趙伶玲. 鍋爐原理[M]. 2版. 北京: 中國電力出版社, 2009: 9.
[5] 張騰飛, 羅銳, 馮文, 等. 爐膛輻射傳熱數學模型及其仿真[J]. 中國電機工程學報, 2003, 23(10): 215-219.
[6] 胡志宏. 超臨界和近臨界壓力區(qū)垂直上升及傾斜管傳熱特性研究[D]. 西安: 西安交通大學, 2001.
[7] 李春燕, 閻維平, 李鈞, 等. 基于矩量法的超臨界鍋爐水冷壁溫度場數值計算[J]. 中國電機工程學報, 2008, 28(32): 29-34.
[8] TALER J, TALER D, LUDOWSKI P. Measurements of local heat flux to membrane water walls of combustion chambers[J]. Fuel, 2014, 115: 70-83.
[9] 李春燕. 超臨界鍋爐水冷壁管溫度數值計算與研究[D]. 保定: 華北電力大學, 2010.
[10] 劉旭聃. 700 ℃超超臨界鍋爐水冷壁壁溫特性研究[D]. 上海: 上海交通大學, 2014.

