中學常見絕對值問題解法的探析

（岳陽市第七中學 湖南岳陽 414000）

關于中學常見的絕對值問題，包括絕對值定義運用問題、一元一次絕對值不等式問題、一次絕對值函數問題、一元一次絕對值方程問題等，針對這些問題，本文分別給出了對應問題的解法，同時為便于理解，本文進行了例題分析。因此，本文對中學常見絕對值問題解法進行深入研究，具有重要意義。[1]

一、絕對值的幾何意義

IaI的幾何意義為：在數軸中，表示原點O和點a之間的距離。Ia-bI的幾何意義為：在數軸中，點a和點b之間的距離。針對一些問題，如果采用絕對值的幾何意義來進行解決，更為簡單、直觀，能夠快速解決問題。[2]

二、一元一次絕對值方程的解法

（1）針對Ia+bI=c（a≠0）型的絕對值方程，其解法為：

②當c＜0時，將絕對值的非負性作為依據，則可以獲知該方程是無解的；

②當c=0時，原方程變為Iax+bI=0，即ax+b=0，則

③當c＞0時，原方程變為ax+b=c或ax+b=-c，

解得或者。

例1：求解I2x+3I=5

解：根據（1）可得，由于5＞0，則原方程可以變形為2x+3=5或者2x+3=-5，解得x=1或者x=-4。

（2）針對Iax+bI=cx+d（ac≠0）型的絕對值方程，其解法為：

①將絕對值的非負性作為主要依據，可得cx+d≥0，進而能夠將x的取值范圍計算出來；

②將絕對值的定義作為主要依據，能夠將原方程進行轉型，變為兩個方程，即ax+b=cx+d和ax+b=-（cx+d）；

③對方程ax+b=cx+d和ax+b=-（cx+d）分別進行求解；

④將計算出來的解，代入cx+d≧0中，對其進行檢驗，將不合條件的解進行舍去。

例2：解方程：I4x+3I=2x+9

解：根據（2）可得，將絕對值的定義作為主要依據，對原方程進行變型，變為兩個方程：4x+3=2x+9和4x+3=-（2x+9）；分別解得x=3和x=-2；通過檢驗后，其結果都是成立的。

（3）針對Iax+b=Icx+dI（ac≠0）型的絕對值方程，其解法為：

①將絕對值的定義作為主要依據，對原方程進行變型，變為ax+b=cx+d或者ax+b=-（cx+d）；

②對方程ax+b=cx+d和ax+b=-（cx+d）分別進行求解。

例3：求解I2x-1I=I3x+1I。

解：根據（3）可得，將絕對值的定義作為主要依據，對原方程進行變型，變為兩個方程，即：2x-1=3x+1或者2x-1=-（3x+1）I3x+1I；分別解得x=-2和x=0。

（4）針對Ix-aI+Ix-bI=c（a＜b）型的絕對值方程，其解法為：

①將絕對值的幾何意義作為主要一種，可得Ix-aI+Ix-bI≧Ia-bI；

②當Ia-bI=c時，方程的解為a≤x≤b；當Ia-bI＞c時，此時方程是沒有解的；

當Ia-bI＜c時，具有兩種情況，即：

①當x＞b時，原方程的解為

②當x＜a時，原方程的解為

例4：求解Ix-1I+Ix-3I=4+-=

解：根據（4）可得，I2-1I＜4能夠劃分為兩種情況，即：

①當x＜1時，原方程的解為x=0；②當x＞3時，原方程的解為x=4。

三、一元一次絕對值不等式的解法

將絕對值符號去掉，使不等式轉型為沒有絕對值符號的一般不等式，然后，和對不等式組或者一般不等式的解法一樣，對以上不等式進行求解，這就是對含有絕對值符號的不等式求解的主要思路。對絕對值不等式進行求解，轉化是關鍵。將絕對值的意義作為主要依據，對絕對值不等式進行有效轉化，使其變為一次不等式。

（1）針對不等式IxI＜a（a＞0），其解集為｛xI-a＜x＜a｝；[3]

不等式IxI＞a（a＞0），其解集為｛xIx＞a或x＜-a｝。

將不等式IxI＜c和IxI＞c（c＞0）中的x進行替換，使其變為ax＋b，便能夠獲得Iax+bI＞c（c＞0）和Iax+bI＜c（c＞0）型的不等式的解法。

（2）Iax+bI＞c（c＞0）的解法為：首先對不等式組ax+b＞c或者ax+b＜-c進行求解，然后根據不等式的性質，對原不等式的解集進行求解。

Iax+bI＜c（c＞0）的具體解法為：首先對不等式組-c＜ax+b＜c進行求解，然后根據不等式的性質，對原不等式的解集進行求解。

例6：對I2x-3I＞4進行求解。

解：根據I2x-3I＞4，可得2x-3＞4或者2x-3＜-4，

然后得到

因此，原不等式解集為

（3）在對Iax+bI＞c（c＞0）與Iax+bI＜c（c＞0）型不等式進行求解時，必須要注

意a是正數還是負數。當a是負數時，可先將a變為正數以后，再進行求解。

例7：求解I1-2xI＜5

根據題意得，-5＜1-2x＜5，則-2＜x＜3。

因此，原不等式的解集是｛x|-5/2＜x＜11/2｝.

（5）含由絕對值的雙向不等式的解法：將絕對值號去掉是關鍵。

例8：求解2＜I2x-5I≤7

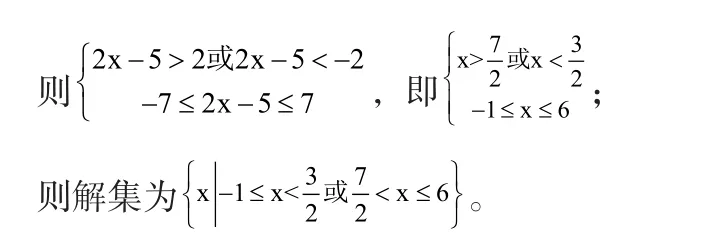
（6）對含有多重絕對值符號的不等式進行求解時，可由外及內的順序進行求解，對絕對值不等式類型的解題方法進行不斷重復運用，將絕對值符號去掉，對其進行一一化解.

例9：求解Ix-I2x+1II＞1

解：根據Ix-I2x+1II＞1可得，x-I2x+1I＞1或者x-I2x+1I＜-1

（1）根據x-I2x+1I＞1可得，x-1＞I2x+1I

（2）根據x-I2x+1I＜-1可得，x+1＜I2x+1I

四、一次絕對值函數的求解方法

在中學階段，一次絕對值函數問題大致可以劃分為4種類型，即：其一，函數圖象；其二，解析式；其三，值域；其四，定義域。經過分類討論后，將絕對值號去除，這是一次絕對值函數問題求解的關鍵。其中，令絕對值內的式子為0是分類標準，進而能夠將數軸劃分為若干段，便能夠進行討論了，然后將函數解析式寫出來，對相應函數圖像進行畫出來，則問題便會變得清晰、明朗。

例10：求解y=Ix+2I-Ix-5I，同時將定義域和值域寫出來。[4]

解：y=Ix+2I-Ix-5I，先分別令x+2=0，x-5=0，可得x=-2，x=5。此時，把數軸劃分為3大段，即：①當x＜-2時，x+2＜0，x-5＜0，因此y=-（x+2）-（-（x-5））=-7；

②當-2≤x≤5時，x+2＞0，x-5＜0，則y=（x+2）+（x-5））=2x-3；

③當x＞5時，x+2＞0，x-5＞0，則y=（x+2）-（x-5））=7;

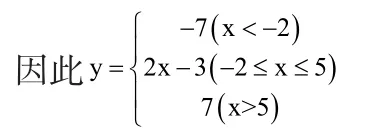
其中，最小值是-7，最大值是7，由此可得，該函數的值域是[-7，7]，定義域是R。

例11：將函數y=Ix-5I+Ix+3I的圖像畫法指出來。

解：①將絕對值符號去除，求出分界點：x-5=0，x=5；x+3=0，x=-3，則分界點就是-3和5；

②根據不同情況進行討論：當x≤-3時，y=Ix-5I+Ix+3I=5-x-x-3=2-2x;當-3＜x≤5時，y=Ix-5I+Ix+3I=5-x+x+3=8； 當x＞5時，y=Ix-5I+Ix+3I=x-5+x-3=2x-8。

③根據上文3個區間所對應的函數解析式，便能夠將帶有絕對值符號的函數圖像畫出來了。

[1]夏福新.中學數學實踐教學初探[J].新課程(中學).2017(01).

[2]曲永安.淺論中學數學創新教學[J].新課程學習(下).2017(04).

[3]劉士斌,楊志華.中學數學“四步試卷講評模式”課例分析[J].時代教育.2017(18).

[4]包麗鷗.基于“四創”教學的中學數學教學研究[J].創新時代.2017(09).