中證100股票指數回歸模型的實證分析

楊思思

（重慶工商大學融智學院 經濟學院，重慶 巴南401320）

一、引言

基金經理經常面臨如何將大額資金快速而方便地投入或撤出股票市場，然而買進或賣出如此大量的個別股票必定會造成價格的劇烈波動，而且也可能違背基金分散投資的宗旨，就要承擔非系統風險。因此，市場的流動性與投資組合的結構是大型基金經理非常關心的課題。

一般情況下，個別股票的操作績效取決于三個因素：整個市場、所屬產業和個別公司[1]。絕大多數分析家認為，整體市場的走勢方向最重要，個股績效可能有70%取決于整體市場的走勢。第二個重要因素是產業的基本面發展趨勢，個股績效可能有20%來自于這方面的影響。所以，個別股票的操作績效大約只有10%來自于特定公司的營運表現。此外，當重大經濟事件發生的時候，通常很容易預測整體股票市場受到的影響，卻難以判別個股反應。為了實現對“整個市場”進行交易，而不是個別股票，金融市場發展出了新的交易工具——股指期貨。不同于其他期貨合約，由于經常劇烈波動，給期貨持有者帶來巨大風險，指數期貨便應運而生。這些產品讓基金經理得以針對市場而不是個別股票來進行交易。于是，各種股票指數與其權重股的研究備受關注[2-3]，能更準確地對實際市場波動情況進行擬合，以及更加真實地反映上證指數的市場風險特性成為建立上證指數模型的重要目標[4]。

本文以中證100股票數據為研究對象，建立中證100股票指數與其成分股的線性回歸模型，利用嶺估計和彈性約束估計分別探討模型中嚴重存在的多重共線性。再通過限定最低門限修正彈性約束估計回歸模型結果，解決模型中部分估計系數為負值的問題。然后去除系數估計值為最低門限值的回歸變量，得到中證100股票指數模型。

二、數據相關性分析

數據來自大智慧軟件，選取中證100指數從2014年6月16日到2014年12月12日之間的日線數據。利用R軟件分析數據并建立模型。

金融市場中的很多變量是相互依存的，但是沒有嚴格的函數關系。線性回歸模型常用來刻畫證券市場眾多的變量關系。然而分析變量間的相關性是建立線性回歸模型的首要任務，于是利用R軟件對因變量Y（中證100指數）與各成分股X1，X2，…，X100之間的相關性進行分析，得到Y與X1，X2，…，X100的相關系數，結果表明有75%的相關系數均大于0.8。因此，建立因變量Y與自變量X1，X2，…，X100的線性回歸模型的初步設想是合理的。

三、建立和診斷模型

（一）建立模型

中證100指數與大多數成分股存在較強的相關關系，因此可以建立中證100指數與各只股票間的線性回歸模型：

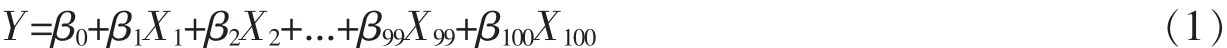
將樣本數據代入上述回歸模型，基于最小二乘法[5]，得到回歸系數β的最小二乘估計值。進一步用模型F檢驗得到p=2.2×10-16，說明模型整體擬合效果不錯，但是仍然存在很多回歸系數無法通過顯著性檢驗。此外，回歸模型中回歸系數估計值出現負值，這顯然與實際意義不符。

（二）診斷模型

線性回歸模型的建立是基于殘差項服從正態分布的假設。為了驗證線性回歸模型（1）的正態假定是否合理，需要對其殘差做夏皮羅-威爾克（Shapiro-Wilk）正態性檢驗[6]。通過R程序計算得到W=0.995 8，顯著概率為0.977，結果表明殘差滿足正態性假設。

另一方面，自變量相關系數矩陣的條件數是度量多重共線性嚴重程度的一個重要指標。實際經驗表明，如果條件數小于100，則認為變量間多重共線性程度較輕微，當條件數大于1 000，則認為存在嚴重的多重共線性。

經計算，模型（1）的100個自變量間相關矩陣的條件數為10 084 240，遠遠大于1 000。再計算其特征值，得到最大特征值為7.55，最小特征值僅為0.000 036 8，均表明模型（1）存在嚴重的多重共線性。此外，計算得到模型的均方誤差(MSE)為429 794。

綜上所述，說明基于所有自變量X1，X2，…，X100的線性回歸模型效果不好，因此需要進一步對模型進行改進。

（三）改進模型

因為模型存在嚴重的多重共線性，所以必須對模型進行改進，而有偏估計是解決多重共線性最直接的方法。其中最常用的是Hoerl和Kennard提出的嶺估計[7]。

嶺估計含有一個參數k，需要利用嶺跡法來選擇參數。其原理在于：嶺估計得到的每個回歸系數βi(k)（i=1,…,100）均是k的函數，當k在[0,+∞)變化時，在平面直角坐標系所描出圖形稱為嶺跡，將100個βi(k)的嶺跡畫在同一個圖上，選擇k使得每個回歸系數的值大體穩定，并且兼顧殘差平方和上升不太多等約束。

通過R程序，繪出嶺跡圖如圖1所示。當k=0.2時，各條曲線基本趨于穩定。

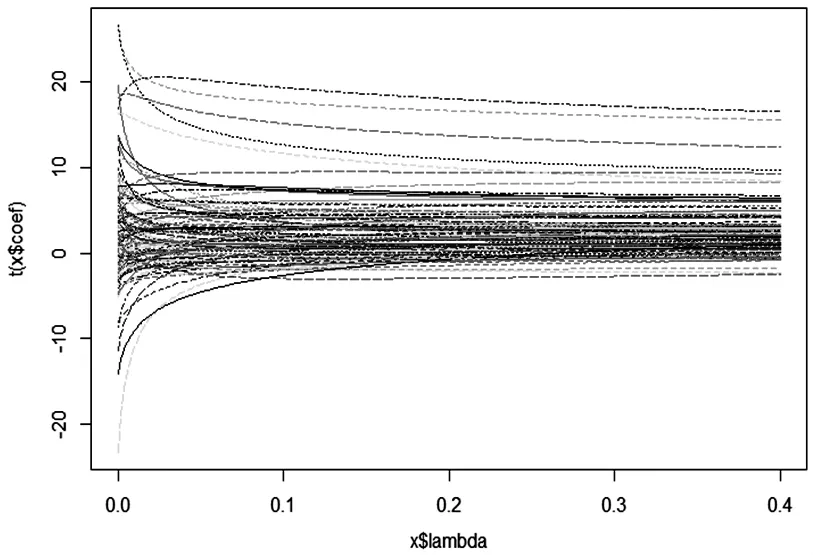
圖1 嶺跡圖

進一步通過函數Select計算，得到如下三種嶺參數：HKB的k值是0.04，L-W的k值是0.004，GCV的最小值是0.04。三種k值均小于0.2，但是L-W的k值太小，計算出來的MSE仍然會很大，于是選擇k=0.04，得到如下的經驗線性回歸方程：

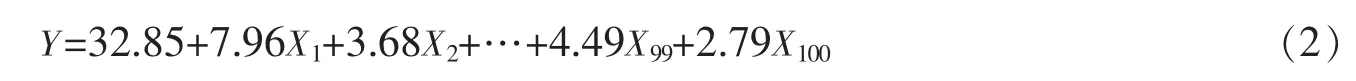
計算得到殘差平方和為81.27，MSE為5 669.44，即表明嶺估計得到的線性回歸方程能夠很好地刻畫中證100股指的趨勢。但是從方程的系數來看，負系數估計值仍然較多并且其絕對值較大，說明模型仍然有待進一步調整。

（四）彈性約束（Elastic net)估計

證券市場中的很多變量是相互依存的，導致多重共線性。因此沒有必要將高度關聯的自變量均考慮到線性回歸模型的建立中。反映在股票上，同一行業內的股票具有很強的相關性，應當選取該行業內具有代表性的一支或者幾支來實現股票指數跟蹤。另一方面，各只股票對指數的影響程度不同，對于影響甚微的股票，沒有必用其成分股來模擬中證100指數。

2005年Zou和Hastie通過合并嶺回歸和LASSO[8-9]，提出了彈性約束估計（Elastic net)正好可以解決上述問題。利用R軟件中的Glmnlet程序包計算得到上述線性回歸模型的彈性約束估計，經過CV交叉驗證[10]，確定最佳λ值為4.53。于是得到含25個自變量的線性回歸模型：

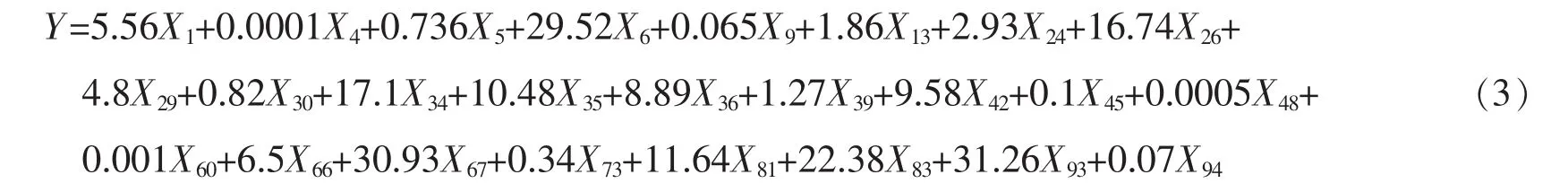
在實際投資實踐中，基金經理需要用最少的股票達到對股票指數的跟蹤。這里通過彈性約束估計得到的最優解僅僅包含了25支成分股，已經能夠滿足持股和利用股指期貨實現風險對沖的目的。此外，計算得到殘差平方和為7 144.95，彈性約束估計殘差圖如圖2所示。因此，根據彈性約束估計建立的線性回歸模型基本上可以模擬出中證100指數的實際走勢，但是擬合效果仍然不是很好。

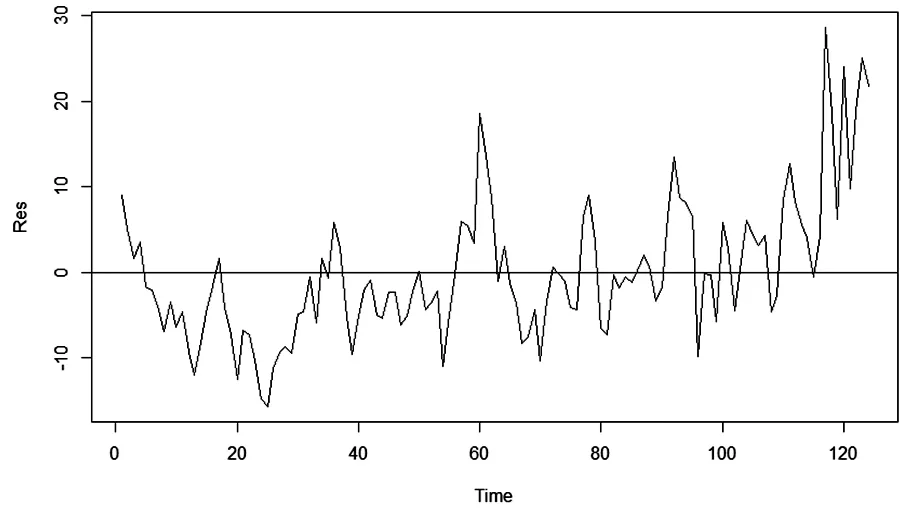
圖2 彈性約束估計殘差圖

（五）修正模型結果

利用彈性約束估計從100只股票中選出了25只，下面將進一步建立股票指數與25只股票的最小二乘線性回歸方程并檢驗其顯著性。

計算結果表明F檢驗高度顯著，大部分變量通過了顯著性檢驗。此外，通過殘差正態性檢驗得到對數正態QQ圖，如圖3所示，只有第60日和第115日的數據不在虛線上。經查看第60日的股票價格和指數并無太多異常，但第115日下一日的股價和指數出現了異常的全體上漲。總體上，修正后的線性回歸模型擬合效果整體不錯，但不足之處在于部分回歸系數仍為負值。

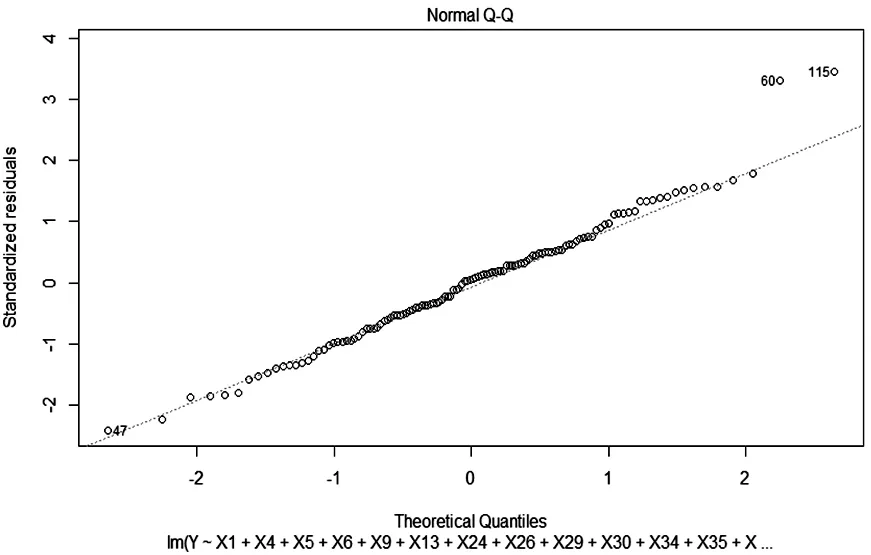
圖3 對數正態QQ圖

而根據實際情況，中證100指數是其成分股走勢的線性組合，受成分股走勢的影響應該為正的。下面對選出來的25個變量建立正回歸，限定最低門限為0.001 36。利用R軟件計算，得到如下的線性回歸模型：

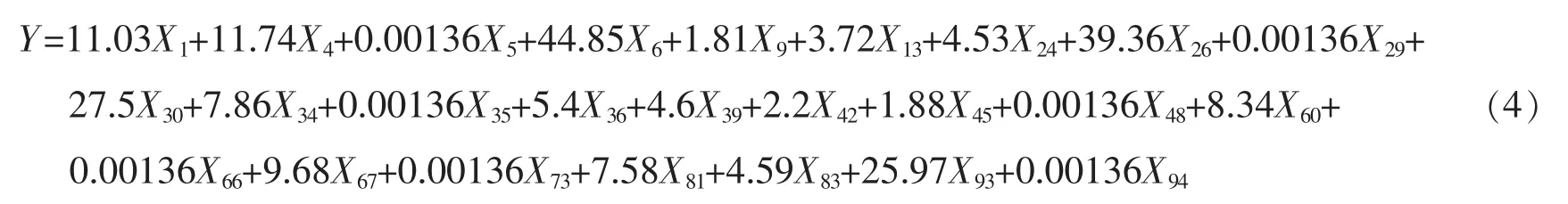
該模型的殘差平方和為3 432，表明模型（4）明顯好于修正前的彈性約束估計模型（3）。

此外，模型（4）中有7個變量的回歸系數是最低門限值，即這7個變量在中證100指數追蹤中所起的作用不是特別明顯。于是嘗試將其舍去，用剩下的18個變量建立中證100指數線性回歸模型為：

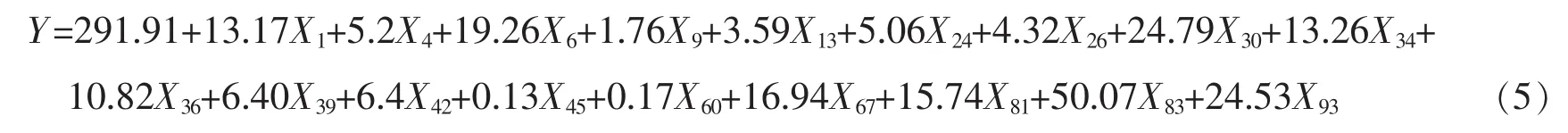
模型（5）的F檢驗高度顯著，只有3個變量未通過p=0.01的顯著性檢驗，并且所有回歸系數估計值均為正數。此外，殘差平方和為1 956，表明它比25支成分股建立的線性回歸模型的效果好。均方誤差（MSE）為142 904，遠遠小于最初100個變量建立的線性回歸模型的MSE。綜上所述，經過此次修正后的股票指數線性回歸模型是最可行有效的。表1是中證100指數回歸模型中成分股股票以及對應的回歸系數。圖4是其股指追蹤效果圖，表明這18只股票可以有效地模擬出指數的實際走勢。

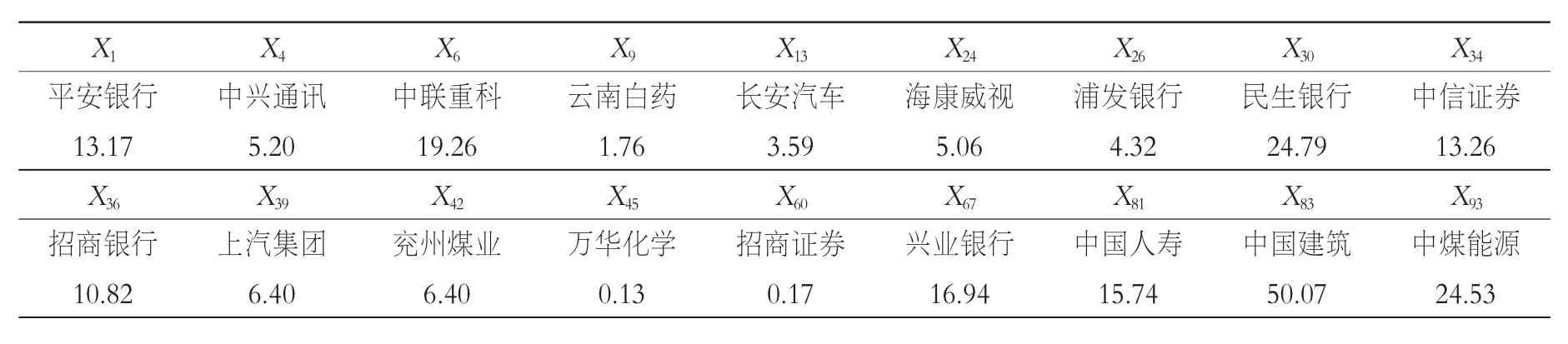
表1 中證100指數回歸模型成分股的權重系數

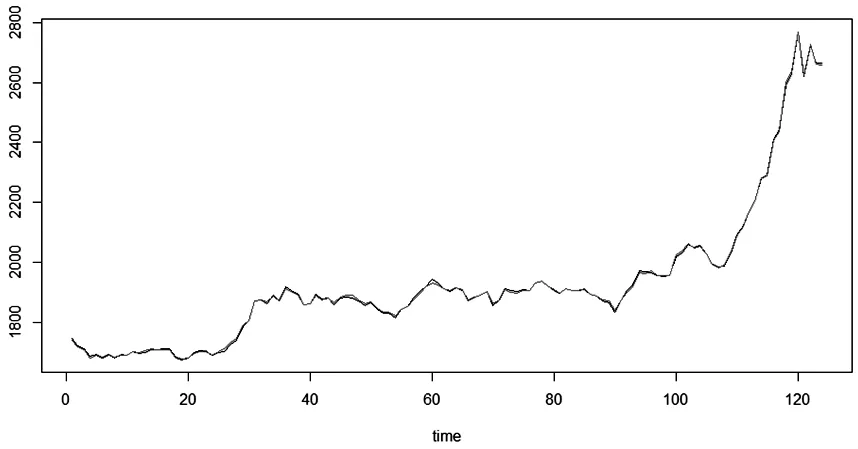
圖4 股指追蹤圖

三、結論

本文以中證100股票指數及其成分股為研究對象，結合模型檢驗并不斷修正模型結果，得到了可行有效、總體效果最佳的中證100股票指數回歸模型。實證分析表明，本文所建立的中證100股票指數回歸模型具有很好的股指追蹤模擬效果，對投資者具有較高的參考價值，能夠在一定程度上降低投資風險，提高股票投資的持續性和穩定性。

[1]彭春.權重股對股票指數影響的實證分析[J].科技經濟市場，2010(9):57-58.

[2]孫秀琳，宋軍.基于權重股的股指期貨操縱模式研究：2007—2008交易數據的實證檢驗[J].世界經濟情況，2009(1):81-89.

[3]楊先明，梁任敏.貨幣供應量對我國股票價格影響的實證分析[M].昆明:云南大學出版社，2013.

[4]周炳均，王沁，鄭興.基于兩種分布下的SV模型與GARCH模型的VAR比較[J].重慶文理學院學報（社會科學版），2016(5):133-137.

[5]陳希孺，王松桂.線性模型中的最小二乘法[M].上海:上海科技出版社,2003.

[6]SHAPIRO S S,WILK M B.An analysis of variance test for normality(complete samples)[J].Biometrika,1965(3-4):591-611.

[7]HOERL A E,KENNARD R W.Ridge regression:Biased estimation for nonorthogonal problems[J].Technometrics,1970(1):55-67.

[8]ZOU H,HASTIE T.Regularization and variable selection via the elastic net[J].Journal of the Royal Statistical Society:Series B,2005(2):301-320.

[9]TIBSHIRANI R.Regression shrinkage and selection via the lasso[J].Journal of the Royal Statistical Society:Series B,1996(1):267-288.

[10]GEISSER S.Predictive inference[M].New York:Chapman and Hall，1993.