幾種復合圖的Bartholdi Zeta函數

陳 語，陳海燕

(集美大學理學院，福建 廈門 361021)

1 預備知識

本文中考慮的圖都是簡單的連通圖.令G是一個簡單圖,V(G)和E(G)分別表示圖G的頂點集和邊集.用degG(v) 表示圖G中v的度,即與v關聯的邊的個數.設C=(e1,e2,…,en)是G的一個閉途徑,令cbc(C)=|{i=1,2,…,n|ei+1=ei}|(這里en+1=e1)表示C中邊回溯的次數.兩個閉途徑C1=(e1,e2…,en) 和C2=(f1,f2,…,fn)稱為是等價的,若存在k使得fj=ej+k(modn),j=1,2,…,k,閉途徑C所在的等價類記為[C].閉途徑C的r次冪表示繞C的次數r所得的閉途徑,記為Cr,若cbc(C)=cbc(C2)=0,則稱C是約化的.進一步,若C不是一個比它嚴格小的閉途徑的冪,則稱C為素的.圖G的Bartholdi Zeta函數定義如下[1]:

其中[C]為跑遍G中素閉途徑的等價類.

當u=0時,Bartholdi Zeta 函數就退化成(Ihara) Zeta 函數[2]:

其中[C]跑遍G中素閉途徑的等價類.

Ihara[2]首先證明了正則圖的Zeta函數ZG(t)的倒數為多項式,隨后相應的結果又被推廣到一般圖上[3].Bartholdi[1]提出了兩個變量的Bartholdi Zeta 函數,并給出了它的一系列性質和它的行列式表達式.此后,針對進一步推廣Bartholdi Zeta 函數以及研究它和圖的各種性質之間的關系，引起了人們的廣泛興趣[4-7].本文中主要討論3種復合圖的Bartholdi Zeta 函數,首先給出它們的定義:給定一個圖G,把G的每條邊e=ab插入一個頂點ce所得到的圖稱為圖G的 剖分圖,記為S(G).對應圖G的每條邊e=(a,b)增加一個頂點ce,并把ce與頂點a和b相連所得的圖稱為G的 三角圖,記為R(G).令I(G)={ce|e∈E(G)},則顯然V(S(G))=V(R(G))=V(G)∪I(G).

定義1已知圖G1和G2,G1和G2的三角點聯圖記為G1∨G2,定義為

V(G1∨G2)=V(R(G1))∪V(G2),

E(G1∨G2)=E(R(G1))∪E(G2)∪

{uv|u∈V(G1),v∈V(G2)}.

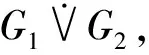
{uv|u∈V(G1),v∈V(G2)}.

定義3[8]已知圖G1和G2,G1和G2的剖分邊聯圖記為G1∨G2,定義為

V(G1∨G2)=V(S(G1))∪V(G2),

E(G1G2)=E(S(G1))∪E(G2)∪{uv|u∈

I(G1),v∈V(G2)}.

2.1 若干預備引理

設G是一個有n個頂點和m條邊的圖,令A(G),D(G),B(G)和L(G)分別表示它的鄰接矩陣、度對角矩陣、關聯矩陣和線圖，則眾所周知[9]:

B(G)TB(G)=A(L(G))+2Im,

這里B(G)T是B(G)的轉置,Im是m階單位矩陣.進一步地如果G是r-正則圖,那么

B(G)B(G)T=A(G)+rIn.

FG(λ,μ)=det(λIn-(A(G)-μD(G))),

則圖G的Bartholdi Zeta函數與廣義特征多項式之間的關系是本文中計算的出發點.

引理1[11-12]設G是n個頂點和m條邊的連通圖,則

FG(λ,μ)=

此外還需要下面關于矩陣的兩個結論:

引理2[12]令M1,M2,M3和M4分別是p×p,p×q,q×p和q×q階矩陣,其中M1,M4可逆，則

2.2 主要結論

本節中給出本研究主要結論及其證明.首先先引入一些符號.

設Jm×n表示m行n列的全一矩陣.M是一個n階矩陣,ΓM(x) 表示(xIn-M)-1所有的元素和,即

給定u,v,令:

(i)β=1-(1-u)2t2,

(ii)γ1=1+(1-u2)t2,

(iii)γ2=1+(1-u)(1+u+n2)t2,

定理1設圖G1是有n1個頂點和m1條邊的r-正則圖,G2是有n2個頂點和m2條邊的任意圖.記r=λ1≥λ2≥…≥λn1為A(G1) 的特征值,則

(2r+n2)(1-u)t2-αn1t-rt)γ1-2rt2]

n2)(1-u)t2-λit)γ1-rt2-λit2]

證明首先由圖G1∨G2的定義知道,它有n1+m1+n2個頂點,3m1+m2+n1n2條邊,所以由引理1,有

ZG1∨G2(u,t)-1=

(1)

對G1∨G2的頂點做適當標號使得其鄰接矩陣和度對角矩陣有如下形式:

D(G1∨G2)=

由引理2可得

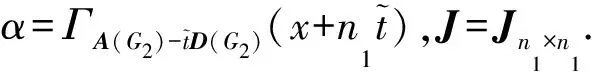
r-λi]，

從而得到下面的關系式:

r-λi].

(2)

再由引理1得

(3)

(1-u)t,整理可得結果.

定理2假設圖G1是有n1個頂點和m1條邊的r-正則圖,G2是有n2個頂點和m2條邊的任意圖.記r=λ1≥λ2≥…≥λn1為A(G1) 的特征值,從而

(r+n2)(1-u)t2-αn1t)γ1-2rt2]·[β+

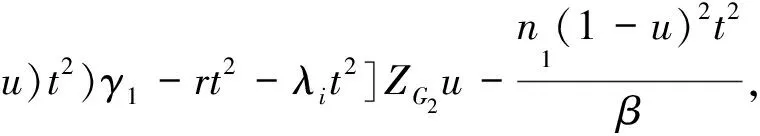
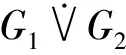
采用與定理1相同的方法計算可得下面的結論.

下面要討論邊剖分邊聯圖G1和G2的Bartholdi Zeta函數.

定理3假設圖G1是有n1個頂點和m1條邊的r-正則圖,G2是n2個頂點和m2條邊的任意圖.記r=λ1≥λ2≥…≥λn1為A(G1) 的特征值,從而

[(γ2-αm1t)(β+r(1-u)t2)-2rt2]

證明由圖G1G2的定義知,它有n1+m1+n2個頂點,2m1+m1n2+m2條邊,所以由引理1,有

ZG1∨G2(u,t)-1=

對頂點進行合適的標號,可以得到G1∨G2的鄰接矩陣和度對角矩陣分別如下:

A(G1

D(G1G2)=

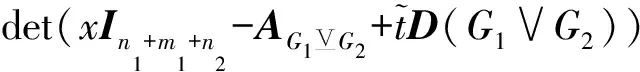
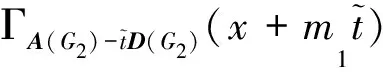
現在回顧兩個結論

(i)Jm1×m1的特征值分別為m1,0,…,0;

(ii) 因為G1是r-正則,所以它的線圖L(G1) 是2r-2-正則.進一步得到A(L(G1))的特征值為λi+r-2,i=1,…,n1,并且特征值-2的重數為m1-n1.

所以本文中可以得到:

后面的證明過程與定理1相似,易得定理3.

證畢.

[1] BARTHOLDI L.Counting paths in graphs[J].Ensignment Math,2000,45(1):83-131.

[2] IHARA Y.On discrete subgrouos of the two by two project linear group over p-adic fields[J].Matematika,1966,18(18):98-115.

[3] BASS H.The Ihara-Selberg zeta function of a tree lattice[J].Internat J Math,1992,3:717-797.

[4] FOATA D,ZEILBERGER D.A combinatorial proof of bass′s evaluations of the Ihara-Selberg zeta function for graphs[J].Trans Amer Math Soc,1999,351:2257-2274.

[5] STARK H M,TERRAS A A.Zeta functions of finite graphs and coverings[J].Adv Math,1996,121:124-165.

[6] STARK H M,TERRAS A A.Zeta functions of finite graphs and coverings,Part Ⅱ[J].Adv Math,2000,154:132-195.

[7] KOTANI M,SUNADA T.Zeta functions of finite graphs[J].J Math Sci U Tokyo,2000,7(1):7-25.

[8] INDULAL G.Spectrum of two new joins of graphs and infinite families of integral graphs[J].Kragujevac J Math,2012,36(1):133-139.

[9] CVETKOVI′C D M,ROWLINSON P,SIMMI′C H.An introduction to the theory of graph spectra[M].Cambridge:Cambridge University Press,2010:217-244.

[10] CVETKOVI′C D M,DOOB M,SACHS H.Spectra of graphs[M].New York:Academic Press,1982:22-28.

[11] KIM H K,LEE J.A generalized characteristic polynomial of a graph having a semifree action[J].Discrete Math,2008,308(4):555-564.

[12] ZHANG F Z.Theschur complement and its applications[M].Berlin:Springer,2005:1-15.