基于隨機模型預測控制的四驅(qū)混合動力汽車能量管理
錢立軍 荊紅娟 邱利宏,2
1.合肥工業(yè)大學汽車與交通工程學院,合肥,230009 2.克萊姆森大學國際汽車研究中心,格林威爾,29607
0 引言
能量管理控制策略對整車的動力性、經(jīng)濟性、舒適性及排放性能具有重要的影響,是混合動力汽車領域的研究重點之一[1]。混合動力汽車的能量管理策略主要包括基于規(guī)則、基于智能、基于優(yōu)化的策略[2]。其中,基于規(guī)則的控制策略簡單實用、控制成本低,卻難以達到全局最優(yōu);智能控制算法魯棒性強、控制靈活,但一般用于優(yōu)化具體參數(shù),不用于過程尋優(yōu);以等效油耗最小策略(equivalent fuel consumption minimization strategy,ECMS)為代表的瞬時優(yōu)化算法執(zhí)行效率高,可以得到近似全局最優(yōu)解,但尚未解決等效因子的最優(yōu)取值問題[3]。全局優(yōu)化算法在已知循環(huán)工況的前提下可以保證整車性能最優(yōu),但是算法程序復雜、運算量大,難以實現(xiàn)實時控制[4]。上述研究工作都是在已知駕駛循環(huán)的基礎上進行的。
有學者采用模型預測控制(model predictive control,MPC)原理對車輛未來行駛狀態(tài)進行預測,利用獲取的預測信息優(yōu)化混合動力汽車轉(zhuǎn)矩分配,提升燃油經(jīng)濟性。BORHAN等[5]認為車輛未來需求轉(zhuǎn)矩按照指數(shù)函數(shù)形式衰減,建立了線性的優(yōu)化控制模型。與基于規(guī)則的控制策略相比,MPC實現(xiàn)了更好的燃油經(jīng)濟性,然而,指數(shù)函數(shù)無法準確預測車輛動力需求。LIN等[6]提出利用馬爾可夫模型預測車輛需求轉(zhuǎn)矩的方法。受此啟發(fā),RIPACCIOLI等[7]將駕駛員需求轉(zhuǎn)矩變化描述為馬爾可夫過程,基于二次規(guī)劃算法(quadratic programming,QP)優(yōu)化動力源轉(zhuǎn)矩分配,改善了燃油經(jīng)濟性并實現(xiàn)了實時計算。針對QP算法應用條件苛刻、線性化過程復雜的問題,BORHAN等[8]建立了非線性優(yōu)化模型并提出采用貝爾曼最優(yōu)化原理求解。目前,MPC方法已被廣泛用于混合動力汽車能量管理。人們不斷探索MPC中車輛動力需求的預測方法以及優(yōu)化問題的求解算法。由于四驅(qū)混合動力汽車能量管理的復雜性,目前用于四驅(qū)混合動力汽車能量管理的控制算法主要有基于規(guī)則、基于ECMS和動態(tài)規(guī)劃(DP)方法[4,9]。
針對上述問題,筆者在所在課題組早前研究基礎[1-4,9-10]之上,提出一種基于馬爾可夫預測模型的四驅(qū)混合動力汽車能量管理控制策略。
1 四驅(qū)混合動力汽車模型
1.1 系統(tǒng)結(jié)構(gòu)
本文研究的對象是一款非插電式四驅(qū)混合動力汽車,其系統(tǒng)結(jié)構(gòu)見圖1。混合動力汽車的前橋和后橋分別由不同的動力源驅(qū)動。前橋由發(fā)動機、啟動一體化(integrated starter-generator,ISG)電機、啟動機聯(lián)合驅(qū)動,驅(qū)動模式由離合器的分離或接合來控制;后橋由后驅(qū)電機單獨驅(qū)動,動力經(jīng)差速器、減速器傳至車輪;逆變器的作用是將電池的直流電轉(zhuǎn)換為交流電,用于給后驅(qū)電機以及ISG電機供電。
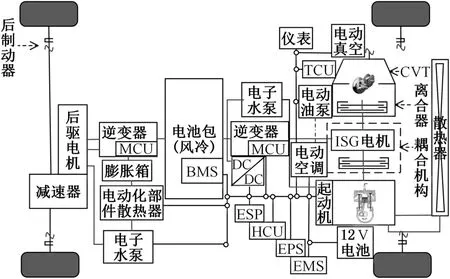
圖1 四驅(qū)混合動力汽車結(jié)構(gòu)圖Fig.1 Configuration of the 4WD HEV
1.2 混合動力汽車動力學模型
四驅(qū)混合動力汽車整車縱向動力學模型[11-12]為

式中,Tq為駕駛員需求轉(zhuǎn)矩,N·m;Cd為空氣阻力系數(shù);Af為迎風面積,m2;v為車速,m/s;m 為整車質(zhì)量,kg;g為重力加速度,m/s2;f為滾動阻力系數(shù);rw為車輪半徑,m;α為坡度角,(°);δ為旋轉(zhuǎn)質(zhì)量換算系數(shù)。
2 馬爾可夫加速度預測模型
若能提前預知混合動力汽車在未來有限時域內(nèi)的行駛狀態(tài),如車速、加速度、需求轉(zhuǎn)矩等信息,便可以在當前時刻運用全局優(yōu)化算法控制車輛性能達到該時域內(nèi)的最優(yōu)狀態(tài)[13]。本文選取加速度作為預測量,將加速度變化描述為一種隨機馬爾可夫過程,即下一時刻的加速度與過去的狀態(tài)無關,僅與當前時刻的速度和加速度相關。車輛未來速度與加速度的概率分布可以從車輛以往行車記錄或標準工況中提取[13]。計算轉(zhuǎn)移概率的關鍵是計算出概率轉(zhuǎn)移矩陣,概率轉(zhuǎn)移矩陣的每一個元素代表汽車加速度從當前狀態(tài)轉(zhuǎn)移到另一個狀態(tài)的概率。選取概率最大的值作為加速度的實際變化路徑,從而確定下一時刻的加速度值。下面給出概率轉(zhuǎn)移矩陣的計算步驟。
采用近鄰法,將加速度離散為有限的數(shù)值:

則當前時刻加速度為ai時,下一時刻加速度為aj的概率為
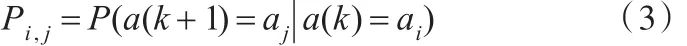
式中,Pi'j為概率轉(zhuǎn)移矩陣的第i行第 j列元素。
Pi'j的值可通過最大似然估計法求得:
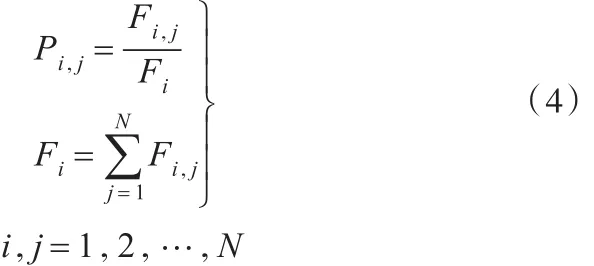
式中,F(xiàn)i'j為加速度從ai轉(zhuǎn)移到aj的次數(shù);Fi為加速度從ai轉(zhuǎn)移的次數(shù)之和。
本文選取新歐洲行駛工況(new European driving cycle,NEDC)、城市道路循環(huán)(urban dynamometer driving schedule,UDDS)和中國城市工況(China urban driving schedule,CUDS)3種工況作為樣本工況來提取車速及加速度數(shù)據(jù)。采樣步長取1 s,工況最高車速為120 km/h,速度離散間隔取20 km/h,工況最大加速度為7.5 m/s2,工況最小加速度為-10 m/s2,加速度離散間隔取0.5 m/s2。將加速度離散成式(2)的形式之后,利用統(tǒng)計分析的知識結(jié)合式(4)計算出每個車速值對應的加速度轉(zhuǎn)移概率矩陣。圖2a~圖2e分別表示車速為30 km/h時加速度的1~5步轉(zhuǎn)移概率。分析圖2可知,加速度的轉(zhuǎn)移概率基本呈對角線分布,說明當前時刻與下一時刻的加速度相差不大,越往后對角線特征越不明顯,這是因為預測步長越長,加速度轉(zhuǎn)移的可能性越多,概率分布就越分散。
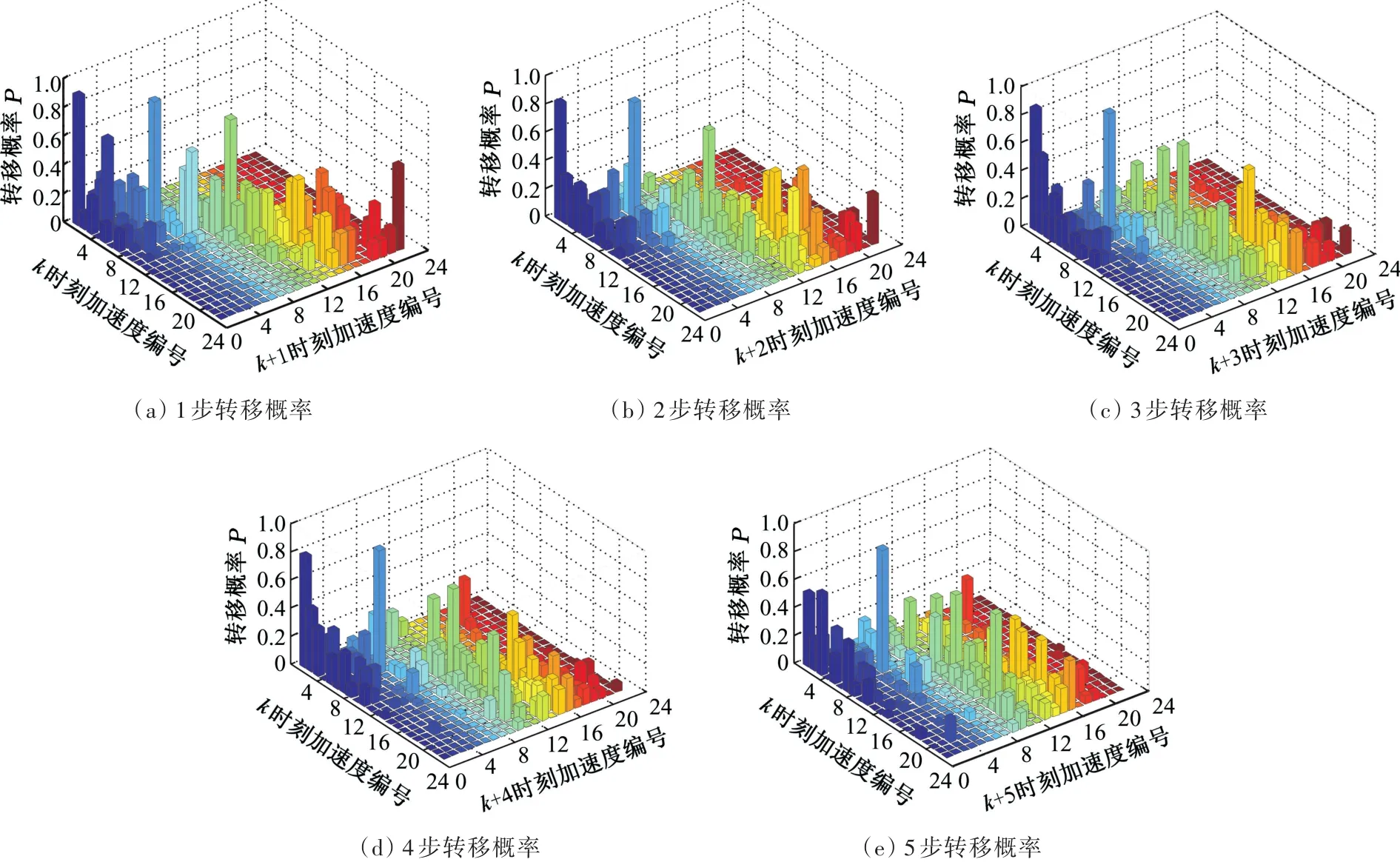
圖2 車速為30 km/h時加速度的轉(zhuǎn)移概率Fig.2 Transition probability of acceleration at 30 km/h
3 四驅(qū)混合動力汽車SMPC控制策略
3.1 SMPC基本原理
隨機模型預測控制(stochastic model predictive control,SMPC)又稱為滾動時域控制,是一種基于滾動優(yōu)化的控制方法,相比于傳統(tǒng)優(yōu)化方法如全局優(yōu)化算法,模型預測控制優(yōu)化算法的最大優(yōu)勢是將優(yōu)化過程限制在有限時域內(nèi),減小計算量,具有實時控制的潛力。SMPC的基本原理可以概括為:在每一個采樣時刻用最新得到的測量值刷新優(yōu)化問題,并求解刷新后的優(yōu)化問題,將得到的優(yōu)化解的第一個分量作用于系統(tǒng),如此循環(huán)往復。
將SMPC應用于四驅(qū)混合動力汽車,實現(xiàn)步驟如下:
(1)建立預測模型。在當前時刻k,根據(jù)式(1)建立馬爾可夫預測模型,預測混合動力汽車未來有限時域k~k+p內(nèi)的車速及加速度,由式(1)計算出車輛在該時域內(nèi)的需求轉(zhuǎn)矩。由k時刻的電池荷電狀態(tài)(battery state of charge,SOC)、發(fā)動機最大轉(zhuǎn)矩、后驅(qū)電機及ISG電機的最大充放電轉(zhuǎn)矩結(jié)合車輛不同的運行狀態(tài),估計出k~k+p時域內(nèi)SOC的最大最小值。
(2)優(yōu)化問題求解。在時域k~k+p內(nèi),建立混合動力汽車能量優(yōu)化目標函數(shù),在給定的約束條件下,采用優(yōu)化算法在SOC可達范圍內(nèi)尋求最優(yōu)控制變量(u(k),u(k+1),…,u(k+p))。
(3)最優(yōu)控制。在SMPC算法中,并不是將最優(yōu)控制全部作用于系統(tǒng),而只實施第一位的控制u(k)。k+1時刻,首先檢測車輛實際車速及加速度,刷新馬爾可夫預測模型,預測k+1~k+p+1時域內(nèi)的車輛運行狀態(tài),再次進行優(yōu)化求解。通過反復地執(zhí)行上述步驟,形成閉環(huán)的反饋控制結(jié)構(gòu),從而提高系統(tǒng)控制精度。
針對四驅(qū)混合動力汽車設計的SMPC控制策略原理見圖3。
3.2 SMPC優(yōu)化控制算法
本文研究的四驅(qū)混合動力汽車的能量管理問題是一個帶約束的非線性優(yōu)化問題。SMPC是在有限時域內(nèi)計算轉(zhuǎn)矩分配,可使計算量大大減小,因此本文采用DP進行求解。
選取發(fā)動機轉(zhuǎn)矩Te作為控制變量,電池SOC作為狀態(tài)變量,即
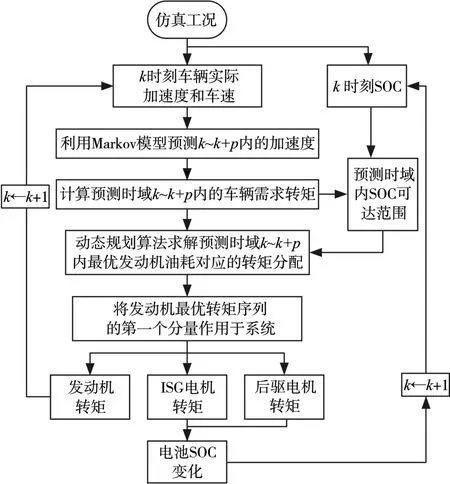
圖3 四驅(qū)混合動力汽車的SMPC控制原理Fig.3 SMPC control principle for the 4WD HEV

式中,SSOC為電池荷電狀態(tài)。
系統(tǒng)在動態(tài)尋優(yōu)過程中,當車輛需求轉(zhuǎn)矩小于后驅(qū)電機能提供的最大轉(zhuǎn)矩時,發(fā)動機不工作;當車輛需求轉(zhuǎn)矩大于后驅(qū)電機能提供的最大轉(zhuǎn)矩但小于前后軸能提供的最大轉(zhuǎn)矩時,發(fā)動機在小于最優(yōu)發(fā)動機轉(zhuǎn)矩的范圍內(nèi)尋優(yōu);制動時發(fā)動機不工作。ISG電機和后驅(qū)電機依據(jù)設定的規(guī)則進行轉(zhuǎn)矩分配。為了避免混合動力汽車兩輪驅(qū)動和四輪驅(qū)動工作模式的頻繁切換,優(yōu)先采用兩輪驅(qū)動。當發(fā)動機轉(zhuǎn)矩為零時,混合動力汽車以純電模式驅(qū)動,優(yōu)先選擇后驅(qū)電機提供驅(qū)動力,不足的部分由ISG電機彌補;當發(fā)動機轉(zhuǎn)矩不為零時,混合動力汽車工作在混合驅(qū)動模式,優(yōu)先采用ISG電機彌補發(fā)動機轉(zhuǎn)矩的不足,此時混合動力汽車工作模式為并聯(lián)前驅(qū);當車輛需求轉(zhuǎn)矩過大時,后驅(qū)電機參與工作,此時混合動力汽車工作模式為四輪驅(qū)動。
系統(tǒng)當前階段的狀態(tài)變量由前一階段的狀態(tài)變量和控制變量唯一確定,系統(tǒng)狀態(tài)轉(zhuǎn)移方程為
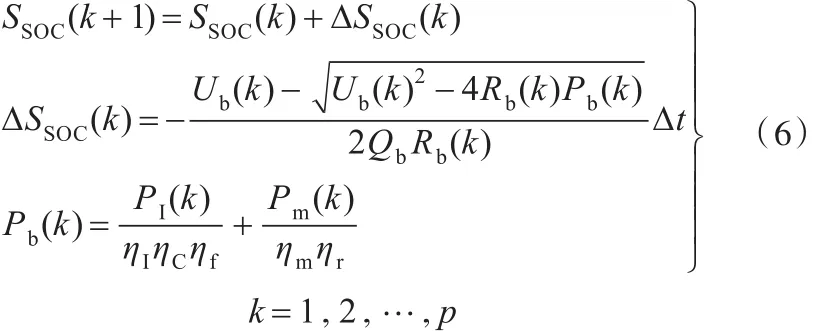
式中,PI為ISG電機功率,kW;Pm為后驅(qū)電機功率,kW;ηI為ISG電機效率;ηC為變速器傳動效率;ηm為后驅(qū)電機效率;ηf為前橋主減速器效率;ηr為后橋主減速器效率;Qb為電池容量,C;Δt為采樣時間間隔,s;Ub、Rb分別為電池端電壓、電池內(nèi)阻,可通過查表獲取。
考慮整車燃油經(jīng)濟性,將混合動力汽車在預測時域p內(nèi)總的燃油消耗作為優(yōu)化目標,則在k時刻建立系統(tǒng)代價函數(shù)如下:
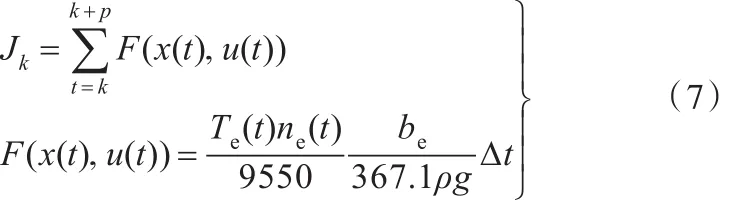
式中,Jk為預測時域k~k+p內(nèi)總的燃油消耗量,L;F為t時刻的瞬時燃油消耗量,L;Te為發(fā)動機轉(zhuǎn)矩,N·m;ne為發(fā)動機轉(zhuǎn)速,r/min;be為發(fā)動機燃油消耗率,g/(kW·h);ρ為燃油密度,kg/L。
為了方便后續(xù)不同控制策略下燃油經(jīng)濟性計算及對比,本文僅考慮發(fā)動機燃油消耗。為了防止在循環(huán)起始和終止時電池荷電狀態(tài)產(chǎn)生較大變化,對燃油經(jīng)濟性的計算造成影響,本文僅考慮混合動力汽車按照電量維持模式工作的情況。為了維持電量的平衡,在進行動力源轉(zhuǎn)矩分配時,需要考慮當前時刻動力電池電量損耗情況,并在下一時刻利用發(fā)動機彌補。根據(jù)電池容量參數(shù),將電池SOC變化設定在初始值2%以內(nèi)。另外,由于混合動力系統(tǒng)各部件受自身工作范圍的限制,現(xiàn)將各變量邊界設置如下:
式中,TI為ISG電機轉(zhuǎn)矩,N·m;Tm為后驅(qū)電機轉(zhuǎn)矩,N·m;ig為CVT變速器傳動比,其值通過查表獲得;if為前橋主減速器傳動比;ir為后橋主減速器傳動比;下標max和min分別表示約束的上下限。
以式(6)為狀態(tài)轉(zhuǎn)移方程、式(7)為目標函數(shù)、式(8)為約束條件,組成的模型預測控制優(yōu)化問題可利用Bellman最優(yōu)化原理進行逆向計算,逐步計算出預測時域內(nèi)的最優(yōu)控制律:
令(SSOC(i+p))=0,則最優(yōu)控制律由下式求得:
圖4為利用Bellman最優(yōu)化原理求解優(yōu)化問題的示意圖。
4 基于dSPACE的軟件仿真
四驅(qū)混合動力汽車主要性能參數(shù)見表1。
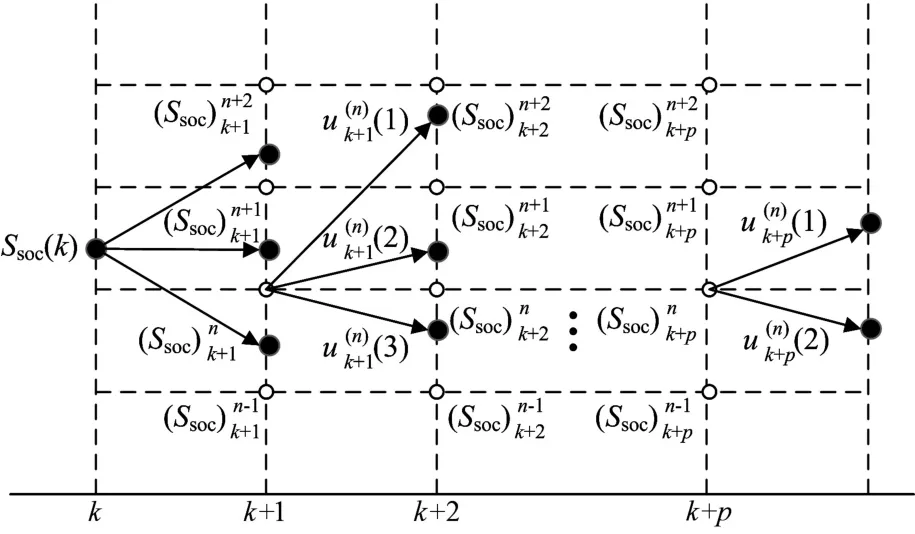
圖4 預測時域內(nèi)最優(yōu)化問題求解示意圖Fig.4 Schematic of solving the optimal problem within prediction horizon
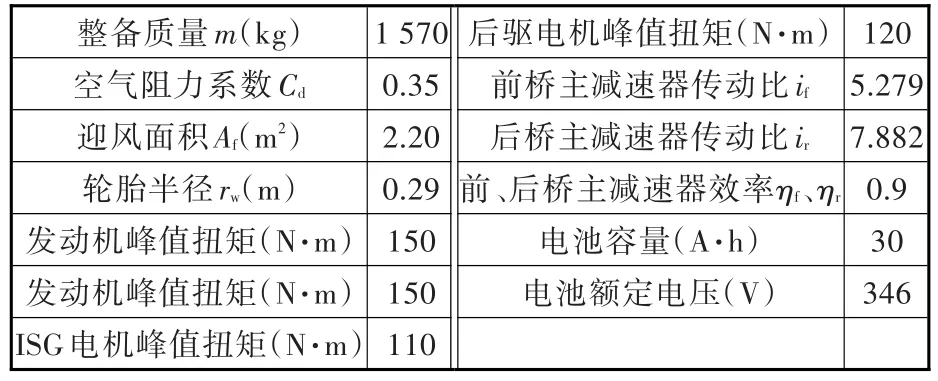
表1 四驅(qū)混合動力汽車主要參數(shù)Tab.1 Main parameters of the 4WD HEV
在MATLAB/Simulink環(huán)境下搭建四驅(qū)混合動力汽車整車模型,根據(jù)本文提出的馬爾可夫預測方法編寫m程序,通過S-Function模塊調(diào)用m程序。將模型編譯后下載到dSPACE中進行仿真試驗。為了縮短仿真總時間,方便仿真結(jié)果對比,本文選取預測時域為5 s,采樣時間間隔為1 s,SOC初始值設為0.5。SMPC控制策略在NEDC工況下的仿真結(jié)果見圖5~圖11。
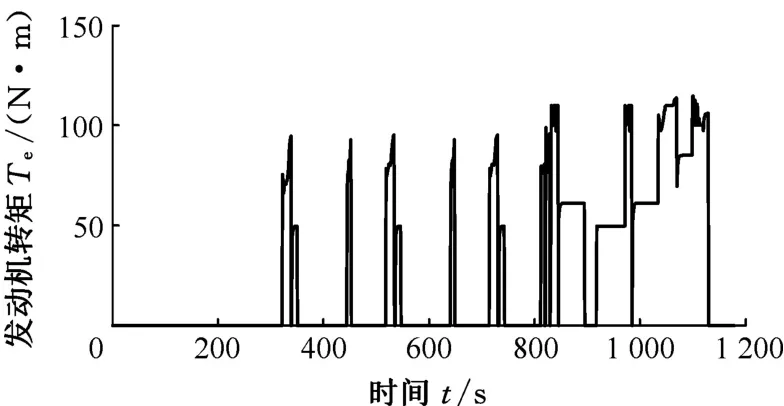
圖5 NEDC工況下發(fā)動機轉(zhuǎn)矩Fig.5 Engine torque over the NEDC cycle
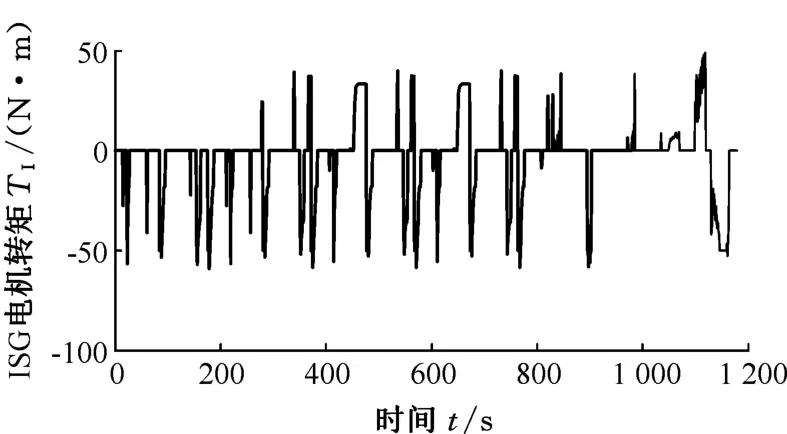
圖6 NEDC工況下ISG電機轉(zhuǎn)矩Fig.6 ISG torque over the NEDC cycle
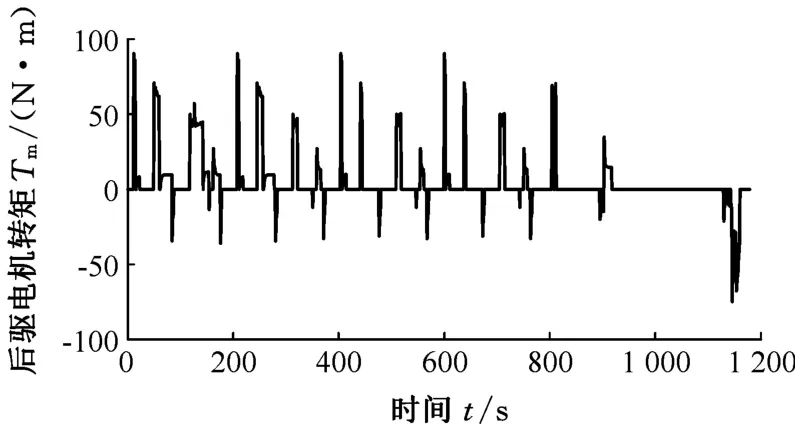
圖7 NEDC工況下后驅(qū)電機轉(zhuǎn)矩Fig.7 Traction motor torque over the NEDC cycle
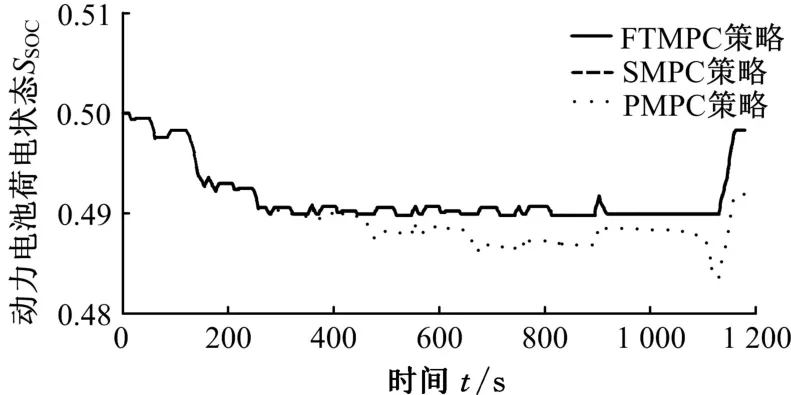
圖8 NEDC工況下SOC變化曲線Fig.8 Battery state of charge over the NEDC cycle
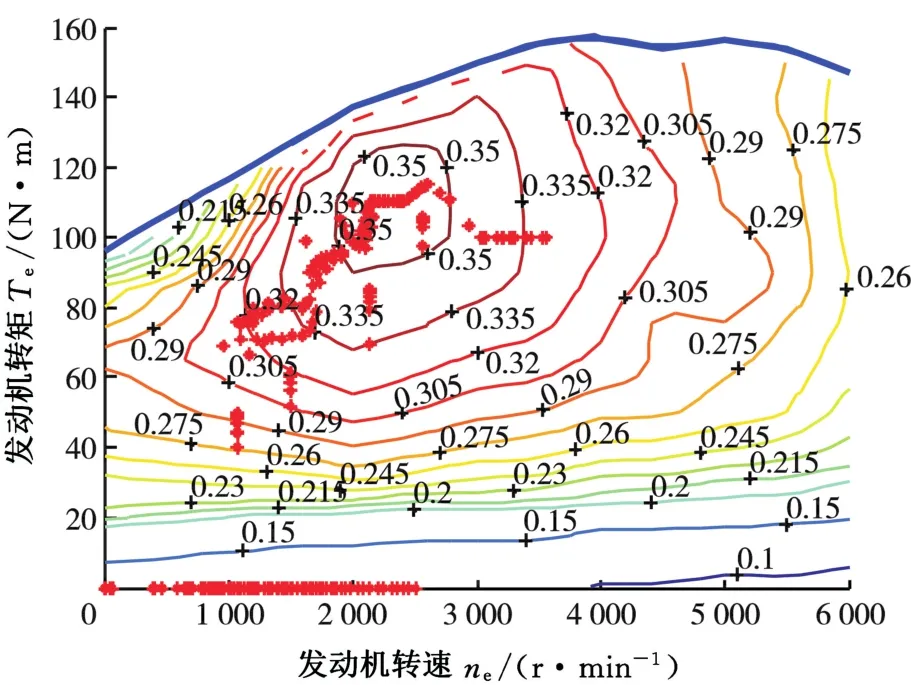
圖9 NEDC工況下發(fā)動機工作點Fig.9 Operating points of the engine over the NEDC cycle
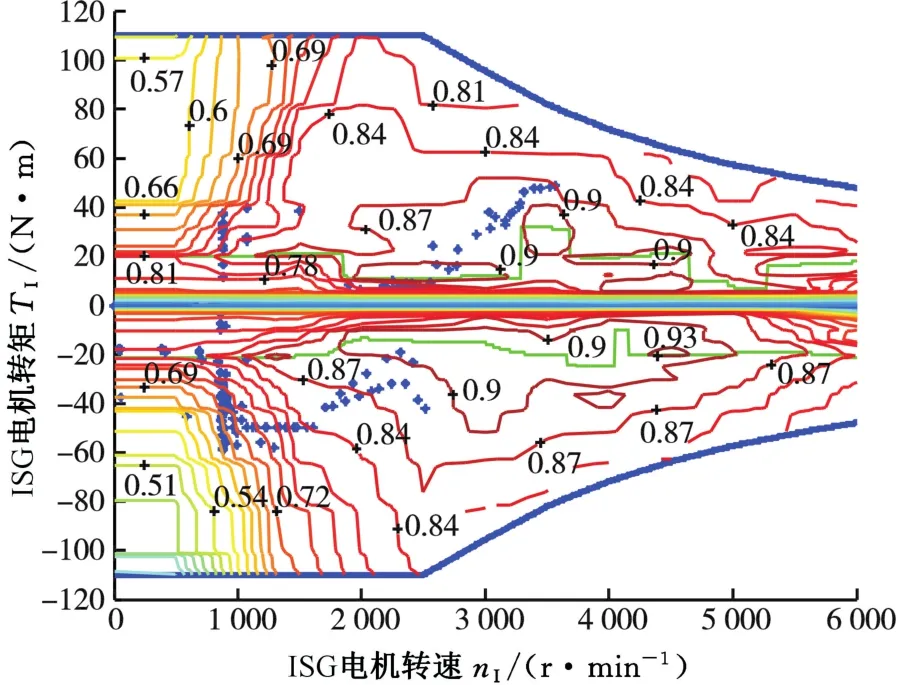
圖10 NEDC工況下ISG電機工作點Fig.10 Operating points of ISG over the NEDC cycle
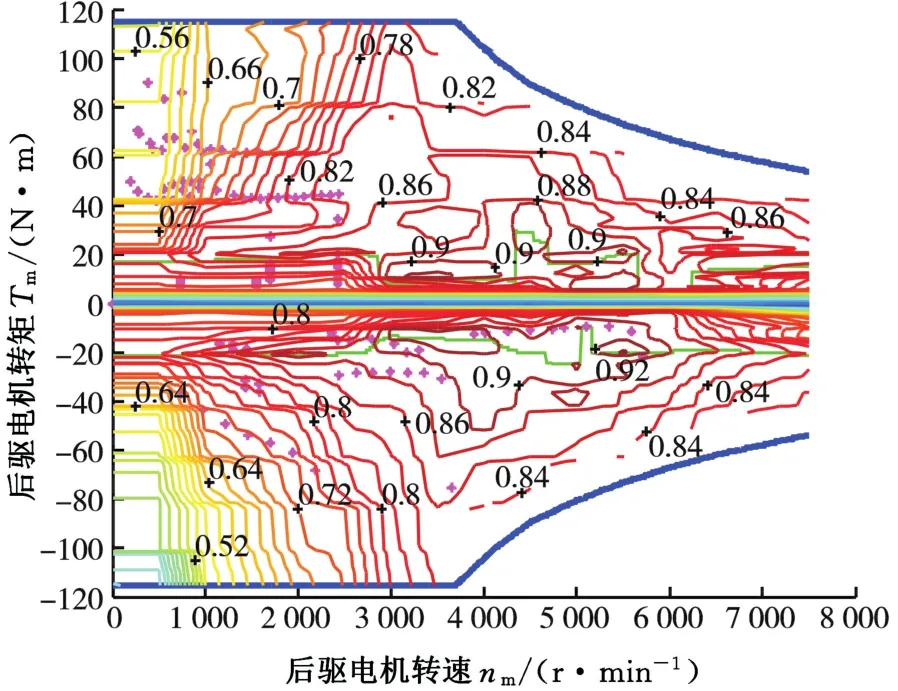
圖11 NEDC工況下后驅(qū)電機工作點Fig.11 Operating points of traction motor over the NEDC cycle
圖5~圖7所示為各動力部件輸出轉(zhuǎn)矩,圖8所示為電池SOC變化曲線。當電池SOC大于0.49時混合動力汽車處于電荷消耗狀態(tài),主要采用后驅(qū)電機驅(qū)動。當電池SOC降低至0.49時,為了保持電池荷電狀態(tài)的平衡,發(fā)動機開始參與驅(qū)動。在整個循環(huán)過程中,混合動力汽車基本工作在兩輪驅(qū)動的模式,避免在兩輪驅(qū)動與四輪驅(qū)動之間的頻繁切換。當車輛需求轉(zhuǎn)矩較小時,由后驅(qū)電機單獨驅(qū)動;當后驅(qū)電機不足以提供全部的驅(qū)動力時,由發(fā)動機和ISG電機驅(qū)動前軸,此時發(fā)動機的工作模式為并聯(lián)前驅(qū);當需求轉(zhuǎn)矩較大時,發(fā)動機、ISG電機和后驅(qū)電機同時啟動,混合動力汽車工作在四驅(qū)模式。在前驅(qū)或四驅(qū)模式,也即是發(fā)動機參與驅(qū)動的情況下,為了調(diào)節(jié)發(fā)動機工作點,使其工作在效率較高的轉(zhuǎn)矩區(qū)域,由ISG電機進行轉(zhuǎn)矩補償。循環(huán)終止時,電池SOC值為0.491 9,與初始值差距很小,整個過程中SOC波動維持在初始值上下2%以內(nèi),說明SMPC控制策略能夠?qū)崿F(xiàn)四驅(qū)混合動力汽車基本的能量管理。
圖9~圖11分別為發(fā)動機、ISG電機和后驅(qū)電機的工作點。由圖9可知,發(fā)動機大部分工作點效率高于0.32,而本文選用的發(fā)動機最高效率為0.36,說明發(fā)動機基本工作在高效率轉(zhuǎn)矩區(qū)域。由圖10、圖11可知,ISG電機和后驅(qū)電機大部分工作點位于0.76~0.9的高效率區(qū)間內(nèi),說明本文提出的SMPC策略具有良好的控制效果。
為了驗證SMPC控制策略的燃油經(jīng)濟性優(yōu)化效果,本文采用另外兩種預測方法作為對比,對混合動力汽車未來有限時域內(nèi)的加速度進行預測。第一種為恒值預測法(frozen-time MPC,F(xiàn)TMPC)[7],即認為預測時域內(nèi)的加速度保持不變,其值等于采樣時刻的加速度值;第二種為具有先驗知識的預測方法(prescient MPC,PMPC)[7],即已知車輛未來加速度、功率需求等信息,其值等于標準工況值。將基于SMPC、基于FTMPC、基于PMPC和基于規(guī)則的策略在3種典型工況下的百公里油耗結(jié)果進行對比,其結(jié)果見表2。
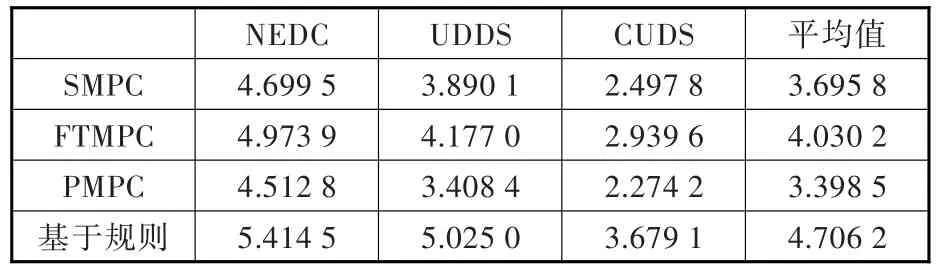
表2 百公里燃油消耗對比Tab.2 Comparison of fuel economy results L
由圖8可知,循環(huán)終止時3種模型預測控制策略的電池SOC值均位于0.49~0.50范圍內(nèi),認為電池荷電狀態(tài)保持平衡,所以本文在進行油耗計算時不計入電池電量消耗,僅考慮發(fā)動機燃油消耗量。由表2可知,本文提出的SMPC控制策略的平均燃油經(jīng)濟性比FTMPC的平均燃油經(jīng)濟性高8.30%。其中,NEDC工況下提升了5.51%,UDDS工況下提升了6.87%,CUDS工況下提升了15.02%,接近PMPC控制策略的燃油經(jīng)濟性。基于PMPC的控制策略預測時域內(nèi)的加速度與車輛實際加速度相同,因而能夠得到較優(yōu)的轉(zhuǎn)矩分配,這種方法類似基于DP的策略,得到的是理想的優(yōu)化結(jié)果,實際上是無法實現(xiàn)的。基于SMPC的控制策略預測時域內(nèi)的加速度是通過分析多種循環(huán)工況預測得到的,基本上能夠反映車輛未來加速度的變化情況,而基于FTMPC的控制策略認為預測時域內(nèi)的加速度保持不變,與車輛實際加速度差別較大。另外,與基于規(guī)則的控制策略相比,基于SMPC的控制策略的平均燃油經(jīng)濟性提升了21.47%。其中,NEDC工況下提升了13.21%,UDDS工況下提升了22.58%,CUDS工況下提升了32.11%。
5 結(jié)論
(1)基于SMPC的控制策略,各動力部件工作情況良好,發(fā)動機、ISG電機和后驅(qū)電機基本工作在高效率轉(zhuǎn)矩區(qū)域內(nèi),證明該策略能夠取得良好的控制效果以及實現(xiàn)四驅(qū)混合動力汽車基本的能量管理。
(2)3種典型工況下,與基于FTMPC的控制策略相比,基于SMPC的控制策略的平均燃油經(jīng)濟性提升了8.30%,接近基于PMPC得到的油耗結(jié)果;與基于規(guī)則的控制策略相比,基于SMPC的控制策略的平均燃油經(jīng)濟性提升了21.47%,說明SMPC策略能夠有效提升四驅(qū)混合動力汽車的燃油經(jīng)濟性。
(3)本文將SMPC控制理論與DP算法有效結(jié)合,實現(xiàn)了四驅(qū)混合動力汽車良好的優(yōu)化控制效果效果,可為進一步研究MPC在混合動力汽車上的應用提供參考。
[1] 錢立軍,邱利宏,陳朋.基于模糊PID扭矩識別的混合動力汽車優(yōu)化控制[J].中國機械工程,2015,26(13):1752-1759.QIAN Lijun,QIU Lihong,CHEN Peng.Optimal Control of a Hybrid Electric Vehicle Based on Fuzzy-PID Torque Identification[J].China Mechanical Engineering,2015,26(13):1752-1759.
[2] 錢立軍,邱利宏,辛付龍,等.插電式四驅(qū)混合動力汽車能量管理與轉(zhuǎn)矩協(xié)調(diào)控制策略[J].農(nóng)業(yè)工程學報,2014,30(19):55-64.QIAN Lijun,QIU Lihong,XIN Fulong,et al.Energy Managementand TorqueCoordination Controlfor Plug-in 4WD Hybrid Electric Vehicle[J].Transactions of the Chinese Society of Agricultural Engineering,2014,30(19):55-64.
[3] 司遠,錢立軍,邱利宏,等.基于等效油耗最小的四驅(qū)混合動力汽車能量管理[J].中國機械工程,2017,28(9):1112-1117.SI Yuan,QIAN Lijun,QIU Lihong,et al.Energy Management of a 4WD Hybrid Electric Vehicle Based on ECMS[J].China Mechanical Engineering,2017,28(9):1112-1117.
[4] 錢立軍,邱利宏,辛付龍,等.插電式四驅(qū)混合動力汽車能量管理控制策略及其優(yōu)化[J].農(nóng)業(yè)工程學報,2015,31(13):68-76.QIAN Lijun,QIU Lihong,XIN Fulong,et al.Energy Management Control Strategy and Optimization for Plug-in 4WD Hybrid Electric Vehicle[J].Transactions of the Chinese Society of Agricultural Engineering,2015,31(13):68-76.
[5] BORHAN H A,VAHIDI A,PHILLIPS A M,et al.Predictive Energy Management of a Power-split Hybrid Electric Vehicle[C]//American Control Conference.Missouri:IEEE,2009:3970-3976.
[6] LIN C C,PENG H,GRIZZLE J W.A Stochastic Control Strategy for Hybrid Electric Vehicles[C]//American Control Conference,Proceedings of the 2004.Boston,2004:4710-4715.
[7] RIPACCIOLI G,BERNARDINI D,DI CAIRANO S,et al.A Stochastic Model Predictive Control Approach for Series Hybrid Electric Vehicle Power Management[C]//American Control Conference.Maryland,2010:5844-5849.
[8] BERHAN H,VAHIDINI A,PHILLIPS A M,et al.MPC-based Energy Management of a Power-split Hybrid Electric Vehicle[J].IEEE Transactions on Control Systems Technology,2012,20(3):593-603.
[9] 邱利宏,錢立軍,程偉,等.插電式串聯(lián)混合動力汽車參數(shù)匹配及控制策略研究[J].汽車工程學報,2014,4(4):297-303.QIU Lihong,QIAN Lijun,CHENG Wei,et al.Parameters Matching and Control Strategy of Plug-in Series Hybrid Electric Vehicles[J].Chinese Journal of Automotive Engineering,2014,4(4):297-303.
[10] 錢立軍,邱利宏,司遠,等.車聯(lián)網(wǎng)環(huán)境下四驅(qū)混合動力汽車隊列能量管理全局優(yōu)化[J].中國科學,2017,47(4):383-393.QIAN Lijun,QIU Lihong,SI Yuan,et al.Global Energy Management Optimization for a Group of 4WD Hybrid Electric Vehicles in Connected Vehicle Environment[J].Sci.Sin.Tech.,2017,47(4):383-393.
[11] RAMADAN H S,BECHERIF M,CLAUDE F.Energy Management Improvement of Hybrid Electric Vehicles via Combined GPS/Rule-based Methodology[J].IEEE Transactions on Automation Science and Engineering,2017,14(2):586-597.
[12] CAI Y,OUYANG M,YANG F.Energy Management and Design Optimization for a Series-parallel PHEV City Bus[J].International Journal of Automotive Technology,2017,18(3):473-487.
[13] ZENG X,WANG J.A Parallel Hybrid Electric Vehicle Energy Management Strategy Using Stochastic Model Predictive Control With Road Grade Preview[J].IEEE Transactions on Control Systems Technology,2015,23(6):2416-2423.

