基于應變梯度塑性理論的紀念幣壓印成形數(shù)值模擬

易國鋒 李巧敏 鐘 文 柳玉起

1.湖北工業(yè)大學機械工程學院，武漢，430068 2.華中科技大學材料成形與模具技術國家重點實驗室，武漢，430074

0 引言

壓印成形是一種重要的金屬塑性成形工藝，廣泛應用于紀念幣的制造過程中。壓印成形的工作機理是：金屬坯餅在模具的作用下發(fā)生塑性變形，最終填充印模型腔，在坯餅的表面印制出精美的圖紋浮雕。由于壓印企業(yè)都是由國家經營，制造技術和工藝方案嚴格保密，現(xiàn)有的公開文獻中，有關紀念幣壓印成形的資料比較少，國內外紀念幣的設計和制造還主要依賴各個造幣企業(yè)長期積累的經驗。工程經驗能夠縮短一些典型紀念幣的研發(fā)周期，卻不能有效地預測壓印成形中金屬的流動情況，因此難以準確預測壓印成形缺陷。據(jù)統(tǒng)計，目前國內造幣行業(yè)紀念幣壓印的廢品率在10%以上，直徑大、鏡面面積大的紀念幣廢品率甚至達到 50%［1］。

針對工程經驗的不足，XU等［2］、鐘文等［3］基于動力顯式有限元法開發(fā)了紀念幣壓印成形數(shù)值模擬系統(tǒng)COINFORM，在壓印成形缺陷預測方面取得了一定成果。對于形狀簡單的樣幣，COINFORM預測的材料流動規(guī)律和壓印力變化曲線與試驗結果吻合較好，但是，出于美觀度、防偽性等因素的考慮，實際的紀念幣上往往會設計精細的圖紋浮雕，這些浮雕的底部圓角在幾微米到幾十微米之間，高度也只有幾十微米到幾百微米。微米量級的變形尺寸導致壓印成形過程中局部區(qū)域的金屬流動規(guī)律與宏觀塑性力學行為不同［4］，而這種尺寸效應在COINFORM的經典塑性本構方程中是沒有考慮的。因此，對于具備精細圖紋浮雕的紀念幣，COINFORM計算得到的結果與試驗結果存在偏差。

為了合理解釋微米和亞微米量級試驗中發(fā)現(xiàn)的尺寸效應，彌補經典塑性理論的不足，很多學者提出了應變梯度塑性理論。FLECK等［5-6］在高階連續(xù)介質彈性理論框架下建立了只考慮旋轉應變梯度的偶應力理論和既考慮旋轉應變梯度又考慮拉伸應變梯度的塑性理論。NIX等［7］從描述材料剪切強度和位錯密度之間關系的Taylor模型出發(fā)，認為應變梯度是由不均勻變形時的幾何必須位錯（geometrically necessary dislocations，GNDs）導致的，通過壓痕試驗得到了壓痕硬度與壓痕深度之間的關系，即 Nix-Gao模型。GAO 等［8］和HUANG等［9］在 Nix-Gao模型的基礎上，提出了一種多尺度、分層次的理論框架，成功實現(xiàn)了塑性理論和位錯理論的結合，發(fā)展了基于細觀機制的應變梯度塑性（mechanism-based strain gradient plasticity，MSG）理論。由于引入了高階應力作為應變梯度的功共軛項，上述應變梯度理論在實際工程應用中遇到了困難。為了簡化高階理論，HUANG等［10］、ZHANG等［11］在 MSG 理論的基礎上提出了傳統(tǒng)的（conventional）MSG理論，即CMSG低階應變梯度理論。CMSG應變梯度理論中的平衡方程以及邊界條件與經典連續(xù)介質力學理論保持一致，因此，本文基于CMSG應變梯度理論建立考慮尺寸效應的本構方程，將其應用于壓印成形數(shù)值模型系統(tǒng)COINFORM中，并通過典型的紀念幣算例對本構方程的準確性進行驗證。

1 基于應變梯度塑性理論的本構方程

1.1 Taylor位錯模型

從微觀角度而言，金屬塑性變形反映了位錯的形成、增殖和運動。位錯運動過程中形成位錯環(huán)和釘扎，在宏觀上表現(xiàn)為金屬的加工硬化。根據(jù)位錯堆垛產生原因的不同，可以將位錯分為統(tǒng)計存儲位錯（statistically stored dislocations，SSDs）和GNDs。其中，SSDs的累積會產生塑性應變，經典塑性理論的Mises等效塑性應變就是SSDs的標量度量，而GNDs是由不均勻塑性變形引起的，與材料的塑性剪切梯度有關。位錯密度ρT定義為單位體積所包含位錯線的長度，即

式中，L為體積V中位錯線的總長度。

材料剪切流動應力τ與位錯密度 ρT之間的關系滿足 Taylor位錯模型［7，12］，即

式中，τ0為內稟點陣阻力，與位錯運動無關，對于Ag這樣的面心立方晶體（face-centered cubic crystal，F(xiàn)CC）而言，τ0為零；α 為經驗系數(shù)，對于 FCC晶體一般取值0.3～0.6［13］；G為剪切模量；b為柏氏矢量的模。

總位錯密度是由SSDs和GNDs耦合作用決定的，耦合關系可以表示為

式中，ρS為SSDs密度；ρG為GNDs密度；指數(shù) μ用來表示ρS與 ρG之間的耦合關系，被命名為“交互系數(shù)”［14］。

μ的選取至關重要，本文認為應該考慮到兩種位錯的非線性耦合，因此根據(jù)試驗來確定μ的取值。

對于材料Ag，根據(jù)式（2）和式（3）可以得到剪切流動應力與位錯密度之間的關系：

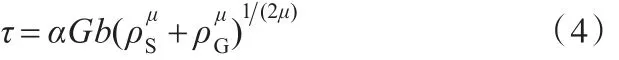
而多晶材料的拉伸流動應力σ與剪切流動應力τ之間滿足

其中，M為取向因子，用來表征連續(xù)介質水平上的各向異性晶體的各向同性程度。FCC晶體的取向因子 M=3.06［15］。由式（4）和式（5）可得

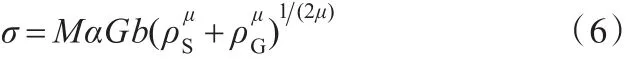
由于 ρG與等效塑性應變梯度 ηp之間滿足［7，16］

其中，rˉ是 Nye因子，在 FCC 晶體中 rˉ=1.90，因此，將式（7）代入式（6）有

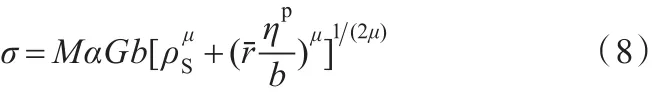
在金屬材料的單軸拉伸試驗中，根據(jù)應力-應變曲線，可以獲得流動應力與塑性應變之間的關系式：

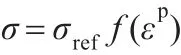
其中，σref為參考應力，f(εp)為塑性應變 εp的量綱一表達式。

單軸拉伸試驗中的塑性應變梯度幾乎可以忽略，即 ηp=0，因此根據(jù)式（8）有

將式（9）代入式（8）可得

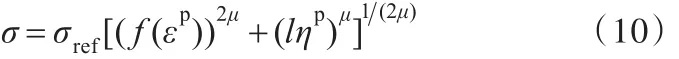
其中式（10）是根據(jù)Taylor位錯模型得到的應力表達式，l為材料內稟尺寸。當金屬變形的特征尺寸遠遠大于l時，式（10）右端的第2項趨近于0，此時式（10）退化成應力-應變關系式：

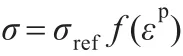
1.2 CMSG塑性理論

根據(jù)CMSG塑性理論框架［10-11］，單軸拉伸試驗滿足以下黏塑性模型：

其中，ε˙p為塑性應變率，和分別為偏斜應力率和偏斜應變率，m為相關指數(shù)。在m→∞的情況下，式（12）與 σ=σreff(εp)等價。為了考慮應變梯度的影響，將基于Taylor位錯模型的流動應力 σ取代式（12）中的 σreff(εp)，獲得

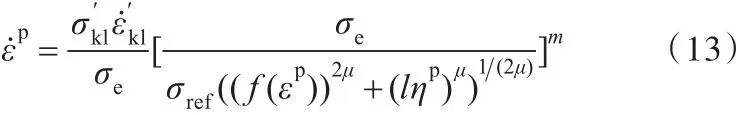
式中，σe為等效應力。

應變率的體積部分 ε˙kk和偏斜部分采用與經典塑性理論相同的表達形式，即

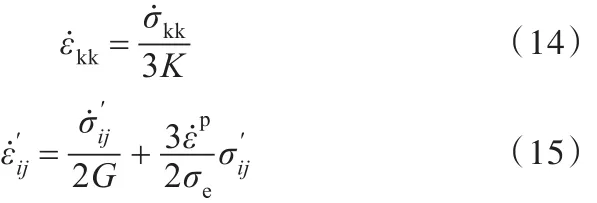
其中，K為體積模量。將式（13）代入應變率的表達式，可以得到基于CMSG塑性理論框架的本構方程：

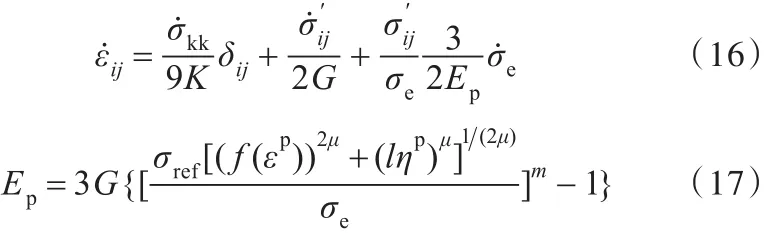
可以發(fā)現(xiàn)，式（16）的表達形式與經典J2流動理論在形式上基本相同，只是將單軸拉伸試驗中的塑性模量 σreff′(εp)替換成了式（17）表示的Ep。隨著應變梯度ηp增大，Ep也會增大，從而帶來額外的流動應力。

2 Ag999的力學性能測試

下面以Ag999為材料對建立的本構方程進行驗證。Ag999的宏觀力學性能參數(shù)見表1［17］。由于用于壓印紀念幣的坯料已經退火處理，因此可以忽略材料的各向異性特性。

為了確定式（17）中的內稟尺寸l和交互系數(shù)μ，本文參考文獻［14］提出的策略，在HYSITRON-TI 750型納米壓痕儀上對Ag999進行納米壓痕試驗。試驗采用Berkovich壓頭，其等效圓錐壓頭的錐面與試樣表面的夾角θ=19.7°，壓頭與試樣的投影接觸面積A與接觸深度hc滿足關系式

表1 Ag999的宏觀力學性能參數(shù)Tab.1 Macro-mechanical properties of Ag999

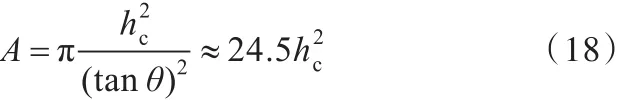
通過納米壓痕試驗獲得的Ag999的載荷-深度（F-h）曲線如圖1所示。從圖中卸載階段的曲線可以看出，Ag999的彈性變形非常小，因此，我們可以將式（18）中的接觸深度hc近似地替換成壓痕深度h，從而簡化接觸面積的計算。根據(jù)圖1中加載階段的F-h曲線和硬度計算公式

可以得到如圖2所示的硬度-深度（H-h）曲線。從圖2中可以看出，在納米壓痕試驗中材料的變形尺度在微米量級，在該變形尺度下，壓痕硬度隨著壓痕深度的增加而逐漸減小。這種尺寸效應與文獻［18-20］中的結論一致。

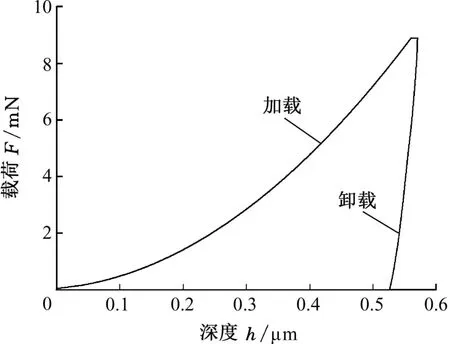
圖1 Ag999在納米壓痕試驗中的載荷-深度曲線Fig.1 Load-depth curve of Ag999 in the nanoindentation test

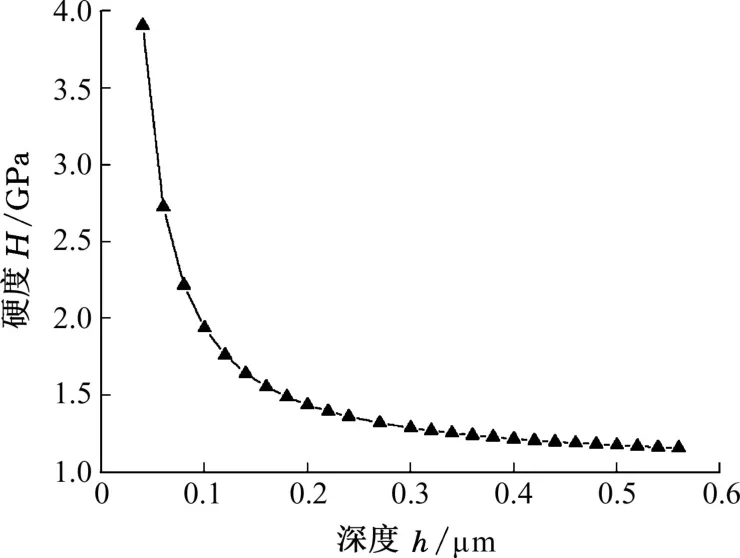
圖2 Ag999在納米壓痕試驗中的硬度-深度曲線Fig.2 Hardness-depth curve of Ag999 in the nanoindentation test

根據(jù)文獻［14］，硬度H、深度h和交互系數(shù) μ滿足關系式：

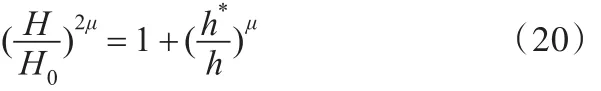
其中，H0為忽略應變梯度時的壓痕硬度值，h*與內稟尺寸l有關，滿足關系式

采用式（20）對圖2中的數(shù)據(jù)進行擬合，擬合結果如圖3所示，其中 H0=1.065 GPa，h*=0.276 μm，μ=1.64。將 h*=0.276 μm 代入式（21），得到內稟尺寸 l=0.976 μm。至此，式（17）所需的所有力學性能參數(shù)均已獲得。

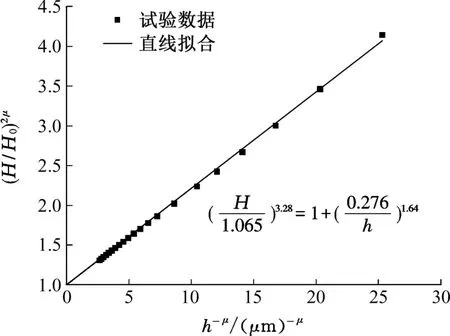
圖3 數(shù)據(jù)擬合Fig.3 Data fitting

3 算例

圖4所示為2010年上海世博會鑰匙紀念幣，采用質量為50 g的Ag999坯餅壓印而成。壓印過程中，上模以100 mm/s的速度向下運動，行程為0.275 mm。印模與坯餅之間的摩擦因數(shù)為0.2。在COINFORM中導入STL格式的印模掃描文件生成三角形網(wǎng)格模型，并采用六面體單元［21］對坯餅進行離散，有限元模型如圖5所示。其中，坯餅單元的個數(shù)為227 504，初始尺寸為270 μm，計算過程中采用3級網(wǎng)格加密。

圖4 2010年上海世博會鑰匙紀念幣Fig.4 A key-shaped commemorative coin of 2010 World Expo

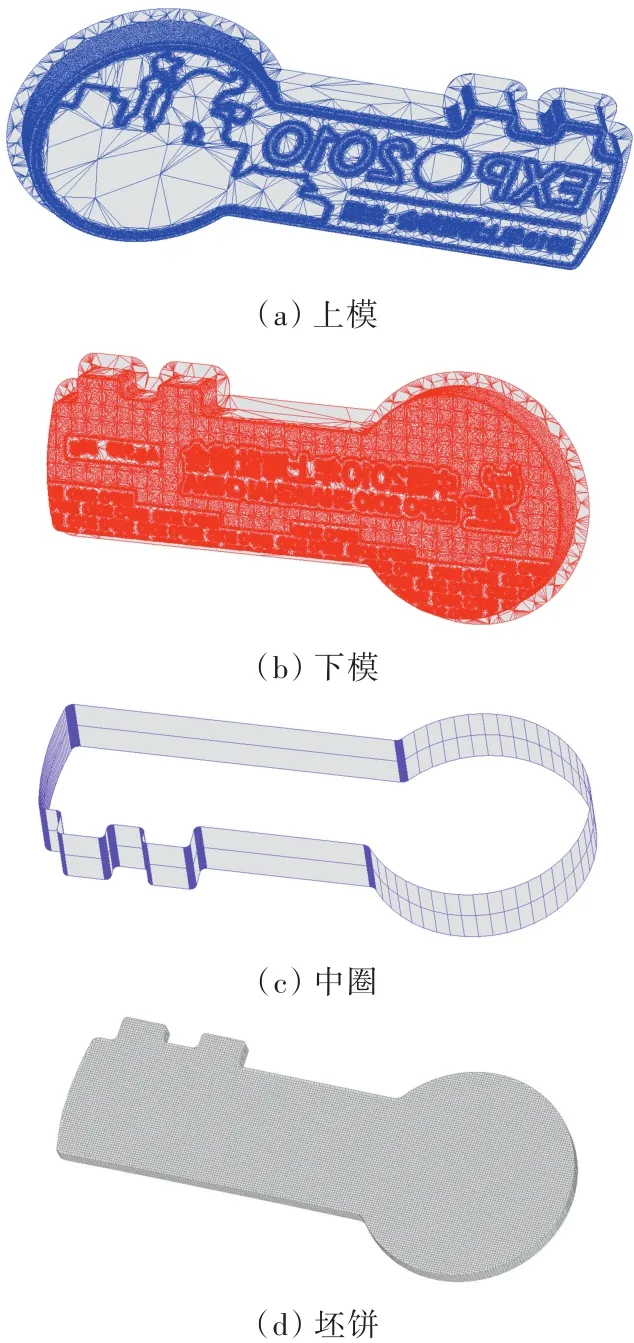
圖5 壓印成形有限元模型Fig.5 Finite element model of coining

將印模視為剛性體，分別采用基于應變梯度塑性理論和經典J2流動理論的本構方程對壓印成形過程進行計算。兩個模擬方案分別耗時5.7 h和5.5 h，可見應變梯度的計算對模擬效率的影響并不大。上模行程達到0.275 mm時的紀念幣等效應力分布如圖6所示。通過對比圖6a、圖6b可以發(fā)現(xiàn)，兩種方案計算得到的等效應力分布規(guī)律整體上接近。但是，在局部浮雕區(qū)域，由于變形尺度很小，應變梯度較大，應變梯度塑性本構方程計算獲得的最大等效應力達到420 MPa，高于經典塑性本構方程計算達到的最大值360 MPa。這說明，對于具備精細浮雕的紀念幣，必須采用比宏觀塑性變形更大的外載荷才能獲得填充飽滿的紀念幣。

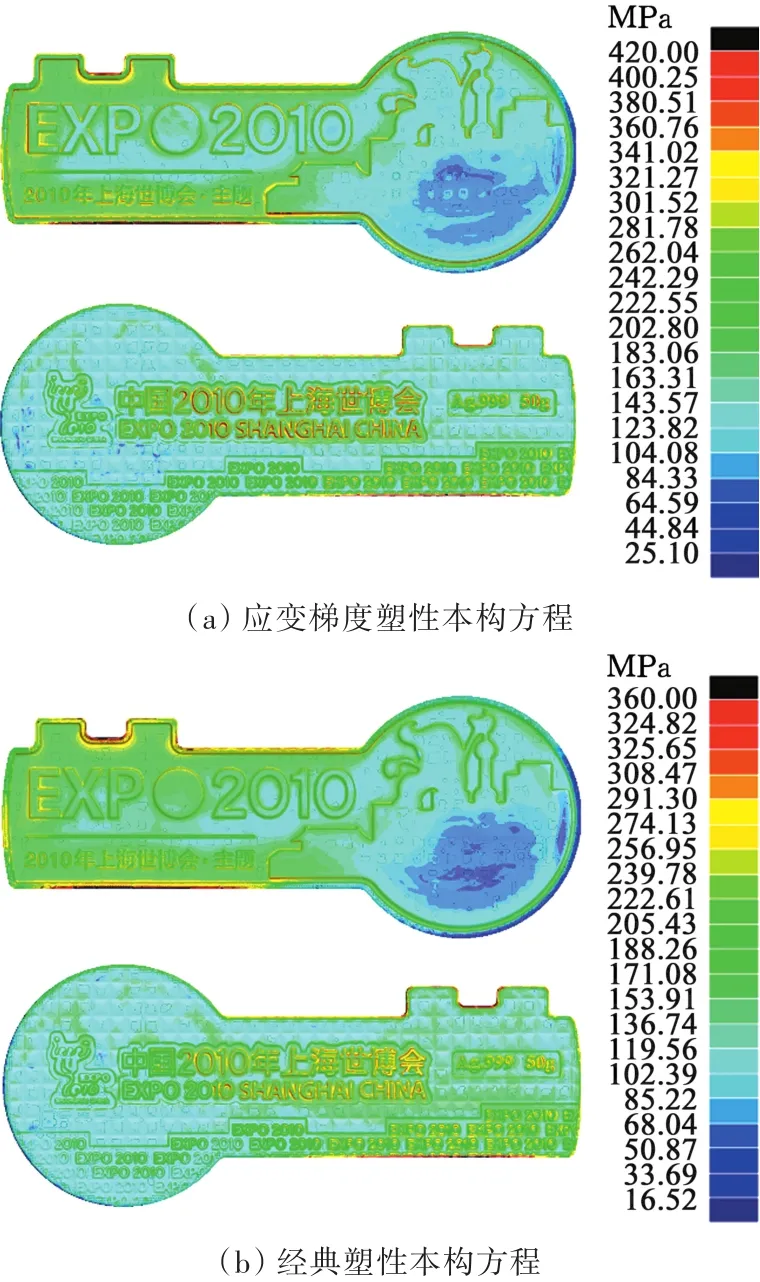
圖6 紀念幣等效應力分布Fig.6 Equivalent stress distribution of the commemorative coin

圖7給出了數(shù)值模擬計算得到的壓印力曲線和試驗測得的壓印力數(shù)據(jù)，其中，試驗獲得的最大壓印力為2 760 kN。從圖7中可以看出，在壓印成形初期，坯餅以整體壓縮成形為主，宏觀塑性變形在成形中占據(jù)主導作用，應變梯度塑性本構方程計算得到的結果和經典塑性本構方程計算得到的結果基本一致。隨著變形繼續(xù)，金屬開始填充微細模具型腔，應變梯度塑性本構方程計算得到的壓印力與試驗結果吻合，計算達到的最大壓印力為2 710 kN，與試驗結果誤差僅為2%；而經典塑性本構方程由于沒有考慮尺寸效應，壓印力計算結果明顯低于試驗結果，且誤差隨模具行程逐漸增大，最終達到14%。因此，本文提出的基于應變梯度塑性的本構方程更加適用于紀念幣的壓印成形模擬。

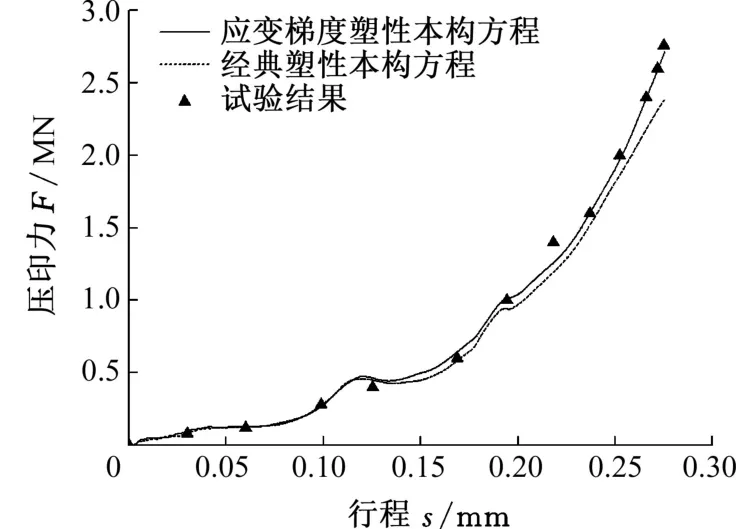
圖7 壓印力-行程曲線Fig.7 Coining force-stroke curve

4 結論

本文從金屬塑性變形的位錯理論出發(fā)，基于CMSG應變梯度塑性理論框架建立了壓印成形的本構方程，以Ag999為例，通過納米壓痕試驗獲得了相關力學性能參數(shù)，并進行了壓印成形數(shù)值模擬。數(shù)值模擬的結果表明，相比經典塑性本構方程，本文所建立的基于應變梯度塑性理論的本構方程在壓印成形中能獲得更高的精度。

［1］ 俞曉萍.北京奧運會紀念幣——從中國走向世界［J］.中國金幣，2008（9）：13-14.YU Xiaoping.Commemorative Coins for Beijing Olympic Games—From China to the world［J］.China Gold Coin，2008（9）：13-14.

［2］ XU J，LIU Y，LI S，et al.Fast Analysis System for Embossing Process Simulation of Commemorative Coin-COINFORM［J］.Computer Modeling in Engineering&Sciences，2008，38（3）：201-216.

［3］ 鐘文，柳玉起，許江平，等.金銀紀念幣壓印成形中的缺陷預測［J］.中國機械工程，2012，23（1）：109-112.ZHONG Wen，LIU Yuqi，XU Jiangping，et al.Defect Prediction in Coining Process for Au-Ag Commemorative Coins［J］.China Mechanical Engineering，2012，23（1）：109-112.

［4］ ZHENG W，WANG G，LIN X，et al.The Experimental Investigation of Size Effect on Micro-cylinder Deformation in Coining Process［J］.Materials and Manufacturing Processes，2014，29（6）：687-690.

［5］ FLECK N A，HUTCHINSON J W.A Phenomenological Theory for Strain Gradient Effects in Plasticity［J］.Journal of the Mechanics and Physics of Solids，1993，41（12）：1825-1857.

［6］ FLECK N A，HUTCHINSON J W.Strain Gradient Plasticity［J］.Advances in Applied Mechanics，1997，33：296-361.

［7］ NIX W D，GAO H.Indentation Size Effects in Crystalline Materials：a Law for Strain Gradient Plasticity［J］.Journal of the Mechanics and Physics of Solids，1998，46（3）：411-425.

［8］ GAO H，HUANG Y，NIX W D，et al.Mechanism-based Strain Gradient Plasticity—I.Theory［J］.Journal of the Mechanics and Physics of Solids，1999，47（6）：1239-1263.

［9］ HUANG Y，GAO H，NIX W D，et al.Mechanism-based Strain Gradient Plasticity—II.Analysis［J］.Journal of the Mechanics and Physics of Solids，2000，48（1）：99-128.

［10］ HUANG Y，QU S，HWANG K C，et al.A Conventional Theory of Mechanism-based Strain Gradient Plasticity［J］.International Journal of Plasticity，2004，20（4/5）：753-782.

［11］ ZHANG F，HUANG Y，HWANG K C，et al.A Three-dimensional Strain Gradient Plasticity Analysis of Particle Size Effect in Composite Materials［J］.Materials and Manufacturing Processes，2007，22（2）：140-148.

［12］ TAYLOR G I.The Mechanism of Plastic Deformation of Crystals.Part I.Theoretical［J］.Proceedings of the Royal Society of London Series A，1934，145（855）：362-387.

［13］ WIEDERSICH H.Hardening Mechanisms and the Theory of Deformation［J］.Journal of Metals，1964，16（5）：425-430.

［14］ VOYIADJIS G Z，Al-RUB R A.Determination of the Material Intrinsic Length Scale of Gradient Plasticity Theory［J］.International Journal for Multiscale Computational Engineering，2004，2（3）：377-400.

［15］ 張帆.CMSG低階應變梯度塑性理論及其應用［D］.北京：清華大學，2005.ZHANG Fan.Conventional Theory of Mechanismbased Strain Gradient Plasticity（CMSG）and Its Applications［D］.Beijing：Tsinghua University，2005.

［16］ ZHANG F，SAHA R，HUANG Y，et al.Indentation of a Hard Film on a Soft Substrate：Strain Gradient Hardening Effects［J］.International Journal of Plasticity，2007，23（1）：25-43.

［17］ LI Q，ZHONG W，LIU Y，et al.A New Locking-free Hexahedral Element with Adaptive Subdivision for Explicit Coining Simulation［J］.International Journal of Mechanical Sciences，2017，128/129：105-115.

［18］ SWADENER J G，GEORGE E P，PHARR G M.The Correlation of the Indentation Size Effect Measured with Indenters of Various Shapes［J］.Journal of the Mechanics and Physics of Solids，2002，50（4）：681-694.

［19］ MCELHANEY K W，VLASSAK J J，NIX W D.Determination of Indenter Tip Geometry and Indentation Contact Area for Depth-sensing Indentation Experiments［J］.Journal of Materials Research，1998，13（5）：1300-1306.

［20］ LEE W B，CHEN Y P.Simulation of Microindentation Hardness of FCC Single Crystals by Mechanismbased Strain Gradient Crystal Plasticity［J］.International Journal of Plasticity， 2010， 26 （10） ：1527-1540.

［21］ 易國鋒，李巧敏，鐘文，等.六面體單元在壓印成形模擬中的應用［J］.中國機械工程，2017，28（15）：1879-1883.YI Guofeng，LI Qiaomin，ZHONG Wen，et al.A Hexahedral Element Applied to Coining Simulations［J］.China Mechanical Engineering，2017，28（15）：1879-1883.