基于自適應無參經驗小波變換和選擇集成分類模型的運動想象?

何群 王煜文 杜碩 陳曉玲 謝平

1 引 言

隨著人類對大腦了解的日益深入和科學技術的迅速發展,腦機接口(brain computer interface,BCI)技術使人們逐漸將思維活動控制現實世界的設想走向現實,該技術不依賴傳統的腦神經和肌肉控制通路,而是通過直接采集大腦的神經生物電信號,構建與外部世界的直接信息傳輸通路[1,2].本文研究的運動想象BCI是基于自發腦活動BCI的典型代表[3].運動想象是指人們只是想象肢體做出某種動作而未實際做出動作.研究發現,運動想象時產生的腦電(electroencephalography,EEG)信號[4]具有和實際動作時EEG信號類似的事件相關同步(event-related synchronization,ERS)和事件相關去同步(event-related desynchronization,ERD)現象,當人們想象某一側運動時,其對側相應大腦皮層區域腦電的mu節律(8—13 Hz)和beta節律(14—30 Hz)頻段幅值降低出現ERD現象,而同側大腦EEG的mu節律和beta節律頻段幅值升高出現ERS現象[5].這種感覺運動區EEG節律的差異是運動想象類BCI的重要特征和依據.

針對EEG信號非線性和非平穩性的特點[6?8],近些年涌現出了很多關于EEG信號的處理方法,如小波變換(wavelet transform,WT)[9]、希爾伯特 -黃 變 換 (Hilbert Huang transform,HHT)[10]、經驗模態分解(empirical mode decomposition,EMD)[11]、總體經驗模態分解(ensemble empirical mode decomposition,EEMD)[12]以及共空間模式(common spatial pattern,CSP)[13]等方法.WT方法不能同時在時域和頻域有較高的分辨率;EMD方法在一定程度上克服了WT方法的不足,相比于WT,其最大的優點是無需事先設定分解層次,但EMD分解后的信號存在邊界效應和模態混疊現象[14];EEMD方法有效解決了模態混疊現象,然而,該方法計算量較大;CSP以及其改進算法被廣泛應用,并取得良好的效果[15],但該方法多用于多電極分布的BCI實驗中.

針對EMD的不足,Gilles[16]結合EMD的自適應性和小波分析的理論框架,提出了一種新的信號處理方法,即經驗小波變換(empirical wavelet transform,EWT).針對傳統的EWT并不能實現頻譜的完全自適應分割的問題,本文采用的自適應無參經驗小波變換(adaptive parameterless empirical wavelet transform,APEWT)[17,18],可以實現頻譜的完全自適應分割.APEWT方法不僅解決了EMD的模態混疊問題,且分解信號所需時間較EEMD短,故本文將APEWT方法應用于EEG信號分析中.當每個受試者在進行運動想象實驗時,發生ERD/ERS現象的時段和頻段不同,經驗主義的判斷無法有效評估每個受試者的最佳時段和頻段[19].針對此問題,文獻[15]根據巴式距離有效選擇出了最佳頻率段,本文方法根據不同時段和不同頻段特征的分類效果為其分配不同的權重,相對單獨考慮最佳頻段更加全面.集成分類器可以得到比單個分類器更優的分類效果,能夠提高學習能力和泛化特性,且較好地解決了特征選擇算法所依據的準則或目標經常與分類器的目標不一致和容易產生選擇的特征并不能滿足分類模型最優化條件的問題[20].因此,本文提出利用APEWT和選擇集成分類模型對運動想象EEG信號進行分類識別,綜合考慮了運動想象EEG信號在不同時段和頻段上的特征,構建了一種選擇集成分類模型,實驗結果證明了該方法的有效性.

2 數據采集與處理

2.1 數據采集

為了驗證本文方法的有效性和普適性,實驗中采用來自兩組競賽數據集的6名不同受試者(S1—S6)的左右手運動想象數據.第一組數據集包含被試S1來自2003年國際BCI大賽Dataset III,包含280個試次;第二組數據集包含被試S2—S6來自2008年國際BCI大賽Dataset 2b,每名受試者包含720個試次,兩組數據的實驗范式略有不同,詳情請見文獻[21,22].

下面主要對第一組數據集進行詳細介紹,受試者是一名健康的25歲女性,所有的實驗(Trails)都在都在同一天進行,實驗包含7組,每組有40個Trails,總共280個Trails.每個Trail持續的時間為9 s,受試者在前2 s處于放松的狀態;在t=2 s時,顯示器出現“+”形圖案,同時有提示音提示受試者實驗開始,“+”保持1 s時間;在t=3 s時,顯示器上出現向左或向右的箭頭,提示受試者按箭頭方向想象用手去移動屏幕上的條形棒,每個Trail數據采集到第9 s結束,運動想象腦電采集范式如圖1所示.實驗使用AgCl電極,數據采集來自C3,Cz和C4三個通道,EEG信號由雙導聯方式記錄,采樣頻率為128 Hz,最終的實驗數據由140個訓練樣本和140個測試樣本組成.

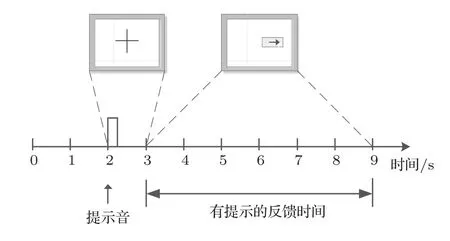
圖1 運動想象腦電采集范式Fig.1.Paradigm of EEG acquisition for motor imagery.

2.2 數據預處理

為了更有效地提取EEG信號的特征,需要對數據進行簡單的預處理.首先去除數據中為“NaN”的空白數據點并置為0,為了降低處理信號的復雜度,對數據集進行了重采樣(250—128 Hz).由于運動想象所誘發的ERD/ERS現象主要是在mu和beta節律段,故采用8—30 Hz的六階巴特沃斯帶通濾波器對原始EEG進行濾波,其阻帶截止頻率為5—33 Hz,阻帶衰減為50 d B,通帶衰減為0.5 d B,對數據集進行統一的濾波處理,以提高信號的信噪比.

3 研究方法

首先,對原始EEG信號進行預處理.然后,使用經APEWT分解后的最優模態重構后的信號和最優模態,分別獲得C3和C4通道的能量譜(energy spectrum,ES)和邊際譜(marginal spectrum,MS)特征,并分別計算C3和C4通道特征的差值,通過加窗的方法得到不同時間段的ES特征和不同頻段的MS特征.具體做法是:將ES特征按時間分為3段,對得到的ES特征以2 s特征為長度滑動分割3—7 s ES特征,步長為1 s特征,將每段重采樣(128—4 Hz)后的ES特征作為基分類器的輸入特征向量;將MS特征按頻率分為10個子頻帶,對得到的MS特征以4 Hz特征為長度滑動分割8—30 Hz頻帶特征,步長為2 Hz特征,將每個子頻帶內的數據作為基分類器的輸入特征向量,分別為每個基分類器的結果分配權重.最后,通過決策分類獲得其最終的分類結果,運動想象模式識別整體流程圖如圖2所示.

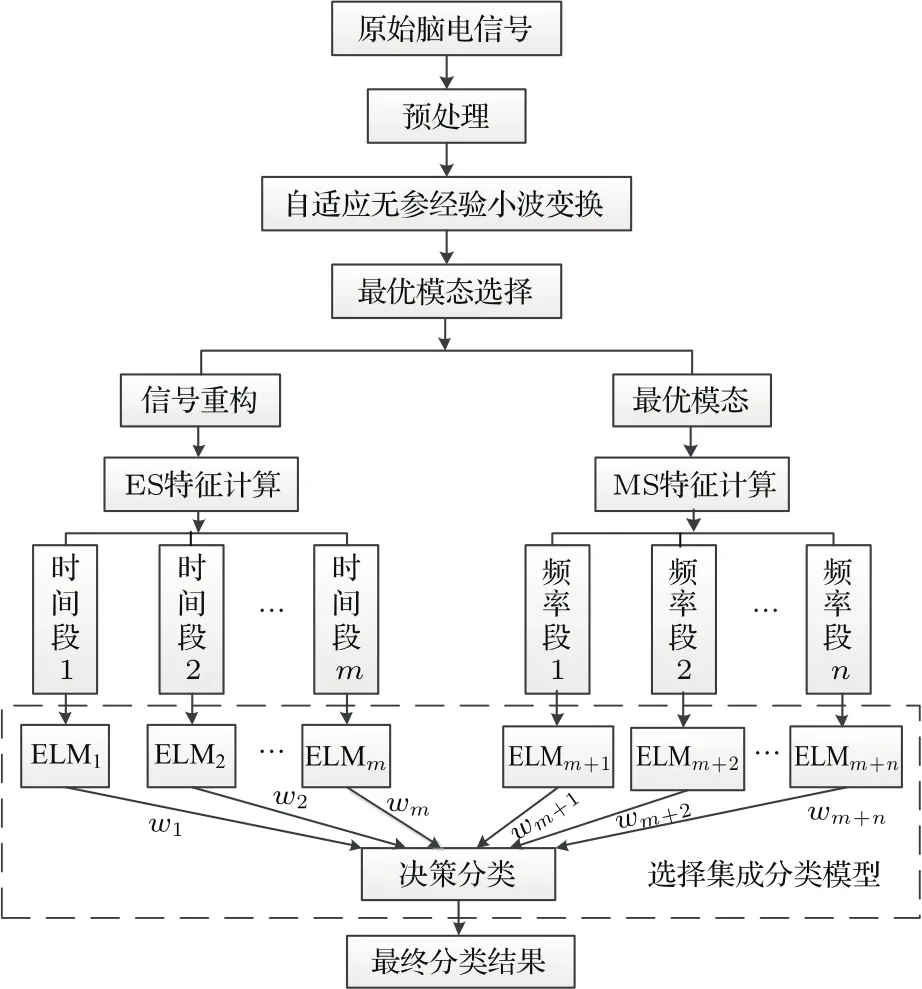
圖2 運動想象模式識別整體流程圖Fig.2.Integrated fl ow chart of motor imagery pattern recognition.

3.1 自適應無參經驗小波變換

EWT將信號f(t)分解成N+1個本征模態函數(intrinsic mode function,IMF)fk(t)之和,表達式為

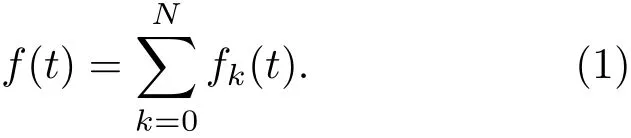
一個IMF函數即為一個調幅-調頻(amplitude modulated-frequency modulated,AM-FM)函數,IMF函數fk(t)定義為

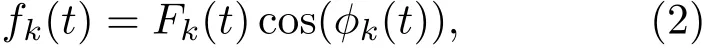
式中Fk(t)>0, ?′k(t)>0, ?′k(t)是 ?k(t)的導數,Fk(t)和?′k(t)的變化速度比?k慢得多. 在EWT中,需要對Fourier譜進行自適應地分割,從而選擇出合適的小波濾波器組.

在確定分割區間后,Gilles[16]根據Littlewood-Paley和Meyer小波的構造方法構造EWT.在EWT中,如何進行頻譜分割是至關重要的,因為它直接關系到分解的結果.APEWT中的Fourier譜分割方法以一種自適應無參的方法自動在直方圖或頻譜中找到有意義的模態為目標,基于所考慮直方圖的尺度空間[23]表示,以更簡單的方式表達“有意義的模態”的概念,該方法的優點是簡單,運行速度非常快.

原始信號f(t)的重構公式為

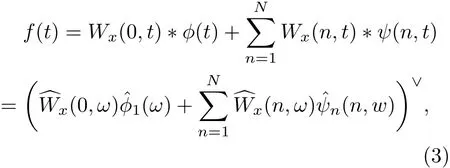
式中?為卷積計算;Wx(n,t)為細節系數,Wx(0,t)為近似系數,?Wx(n,t)和?Wx(0,t)分別為Wx(n,t)和Wx(0,t)的Fourier變換;?(w)為經驗尺度函數,ψn(w)為經驗小波函數,??(w)和?ψn(w)分別為?(w)和ψn(w)的Fourier變換.

本征模態分量fk(t)定義如下:

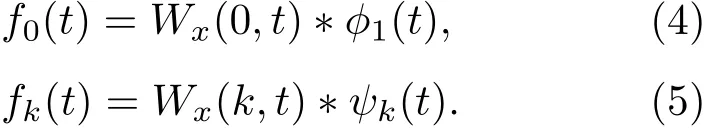
3.2 最優模態選擇

EEG信號經APEWT分解后,模態分量較多,但某一動作模式下的對應區域EEG信號主要集中在特定頻段,因此選取能量最為集中的分量是非常必要的.本文借鑒文獻[24]中方法,將APEWT分解后的各模態與原始EEG信號的相關系數作為評定各模態分量的指標,定義如下:

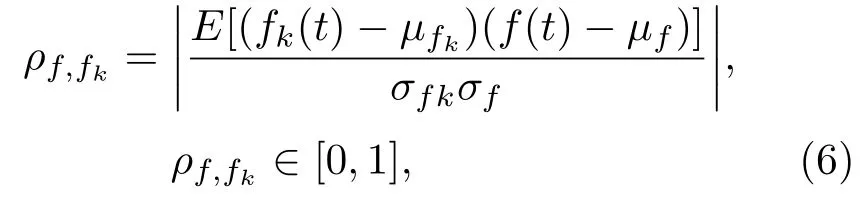
式中fk(t)和f(t)分別為APEWT分解后的各模態分量和原始信號;μfk,σfk,μf,σf分別為fk(t)和f(t)對應的時域均值和標準差;E為數學期望.ρf,fk反映了模態分量fk(t)與原始信號f(t)在時域中的相關性,其數值越大,表明模態分量與原始信號越相關,因此可根據ρf,fk的數值大小選擇有效模態分量.

3.3 ES特征

對選出的模態按(3)式進行重構,信號重構后,由(7)式求取ES特征:

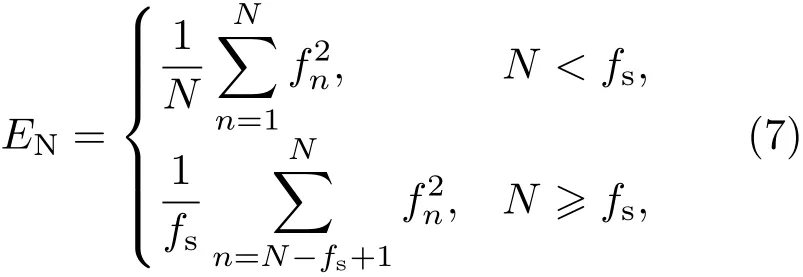
式中f2n指Trail中某通道信號重構后第n個采樣點瞬時幅值的平方;EN表示求出的平均瞬時能量特征;fs為采樣頻率.當Nfs時,計算N個采樣點之前fs個數據幅值平方的平均.

3.4 M S特征

Fourier頻譜的某一點頻率上的幅值表示在整個信號里有一個含有此頻率的三角函數組分,而MS從統計意義上表征了整組數據每個頻率點的累積幅值分布,MS能夠處理非平穩信號,如果信號中某一頻率的能量出現,就表示一定有該頻率的振動波出現,所以MS能比較準確地反映信號的實際頻率成分,而Fourier變換只能處理平穩信號,故文中使用MS特征.

對選出的IMF分量信號fk(t),(k=1,2,···,n)進行變換得

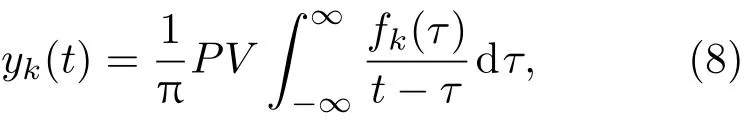
式中PV為柯西主值,則進一步得到zk(t)的解析式為

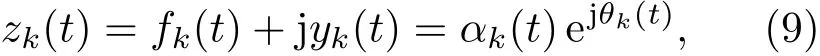
式中αk(t)代表瞬時幅值;θk(t)代表瞬時相位.希爾伯特變換的瞬時頻率定義為

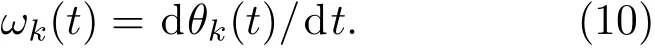
其希爾伯特譜定義為

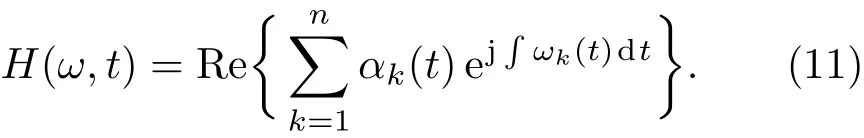
MS的定義為

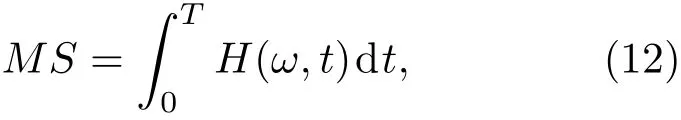
式中T為信號長度.

3.5 選擇集成分類模型

本文根據運動想象的ES特征和MS特征,采用選擇集成分類模型對左右手運動想象EEG信號進行分類識別.

Huang等[25]提出了極限學習機(extreme learning machine,ELM)算法.該算法與BP(back propagation)等神經網絡算法相比,大大提高了網絡的泛化能力和學習速度,同時避免了陷入局部最優的風險.相比于ELM,支持向量機和最小二乘支持向量機更趨向于得到次優解,而且也都沒有考慮多層前饋神經網絡中隱層的特征表征[26].故本文將ELM作為選擇集成分類模型的基分類器,單隱層前饋網絡隱層節點個數為25,隱層激活函數為Sigmoid.

對于集成分類模型中權重的設置,假設每個基分類器對于訓練集的分類正確率為A=[A1,A2,···,AM],權重計算式為

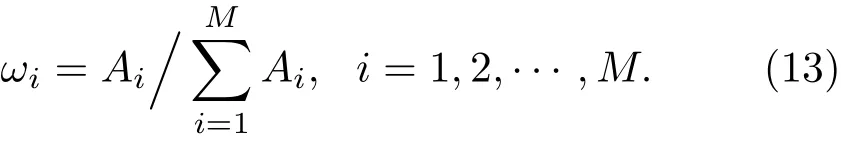
在集成分類模型中,若存在分類效果較差的基分類器將會影響最終的分類結果,所以本文對基分類器進行了選擇.將基分類器訓練集的準確率按照從大到小的順序進行排列,以預測結果最優為原則,選擇分類效果較好的α個基分類器,具體選擇方法如下:

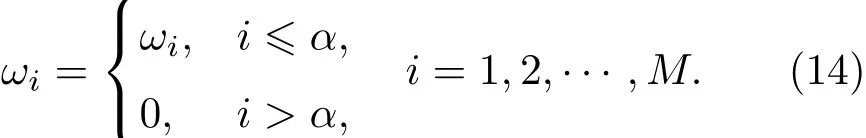
通過對基分類器的篩選,獲得了較好的集成分類模型.假定有M個待集成的基分類器Ci(i=1,2,···,M),每個基分類器的預測標簽結果為Ci(n),n為數據集中的樣本數.選擇集成分類模型為?C(n),則有

式中ωi滿足f為集成規則.

具體的集成規則為:假設有k個基分類器的分類結果為左手,l個基分類器的分類結果為右手,其中k+l=M,若則集成分類器的結果為左手,否則為右手.

4 實驗結果

本文方法的實驗環境為Windows 64位系統,4 GB內存,CPU主頻為1.80 GHz,仿真軟件為MATLAB R2013 b.

4.1 信號分解與模態選擇

受試者S1某一試次的運動想象EEG信號分別經EMD和APEWT分解后各階模態分量和頻譜圖如圖3所示.

由頻域圖3(b)和圖3(d)可知,使用APEWT進行EEG信號分解的效果明顯優于EMD.

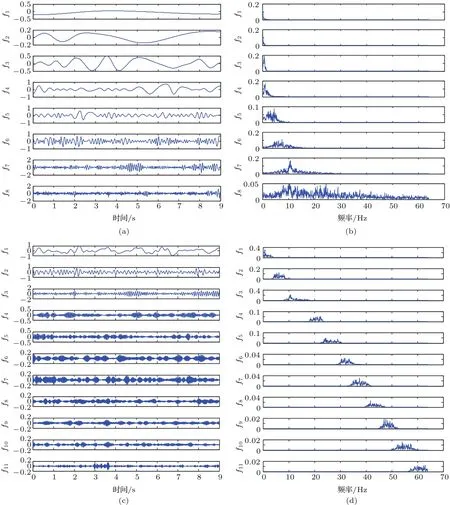
圖3 EEG信號分解結果 (a)EMD分解得到的IMF分量;(b)EMD分解的得到的IMF分量頻譜;(c)APEWT分解得到的IMF分量;(d)APEWT分解的得到的IMF分量頻譜Fig.3.EEG signal decomposition results:(a)EMD-based IMF components and(b)their corresponding frequency spectra;(c)APEWT-based IMF components and(d)their corresponding frequency spectra.

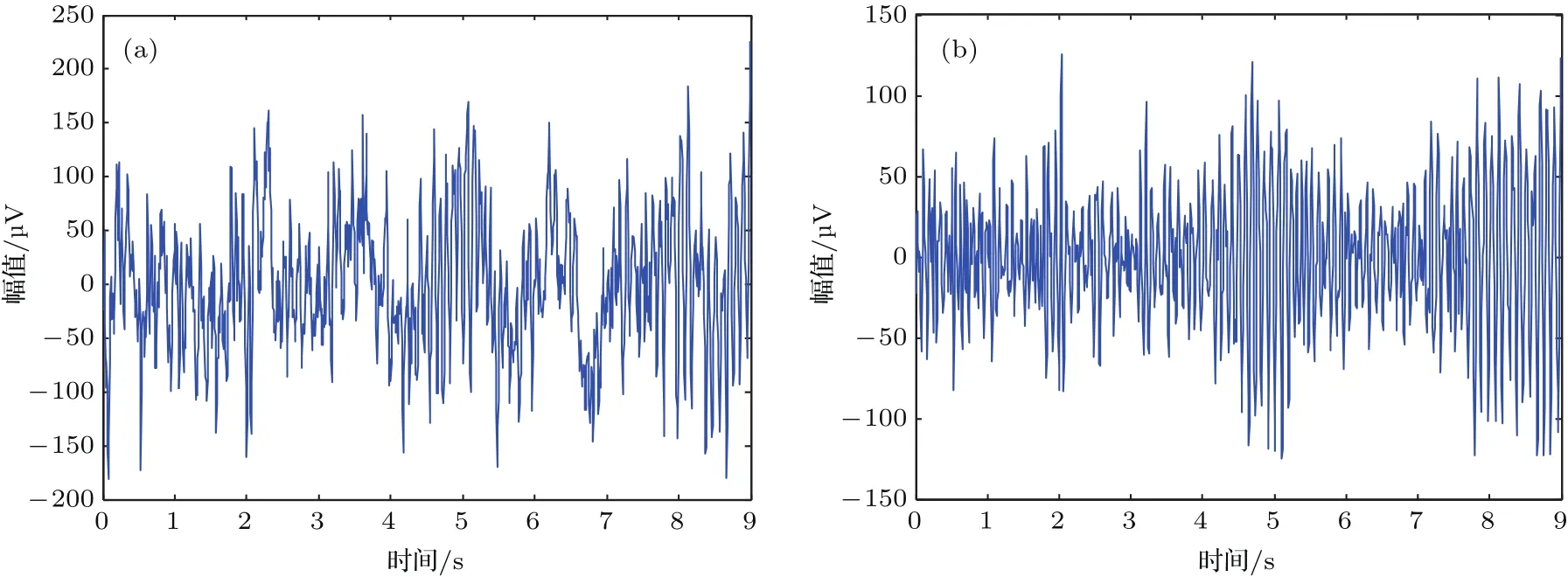
圖4 運動想象EEG信號 (a)原始EEG信號;(b)重構后EEG信號Fig.4.EEG signals of motor imagery:(a)Original EEG signal;(b)reconstructed EEG signal.

基于(6)式計算并選取相關系數閾值ρf,fk>0.5[24],獲得有效分量,分解后有效模態分量主要集中在f3,f4和f5分量上;同時由各分量的頻譜圖分析可知,mu節律和beta節律頻段相應的信號也主要集中在f3,f4和f5分量上,從而選定這3個分量進行信號重構,原始信號和重構信號如圖4所示.

4.2 ES特征和M S特征

為了更好地表現ES特征和MS特征C3和C4兩個通道的關系,分別計算了6名受試者3—7 s的所有試次的ES特征和MS特征.運動想象EEG ES特征和MS特征分別如圖5和圖6所示.

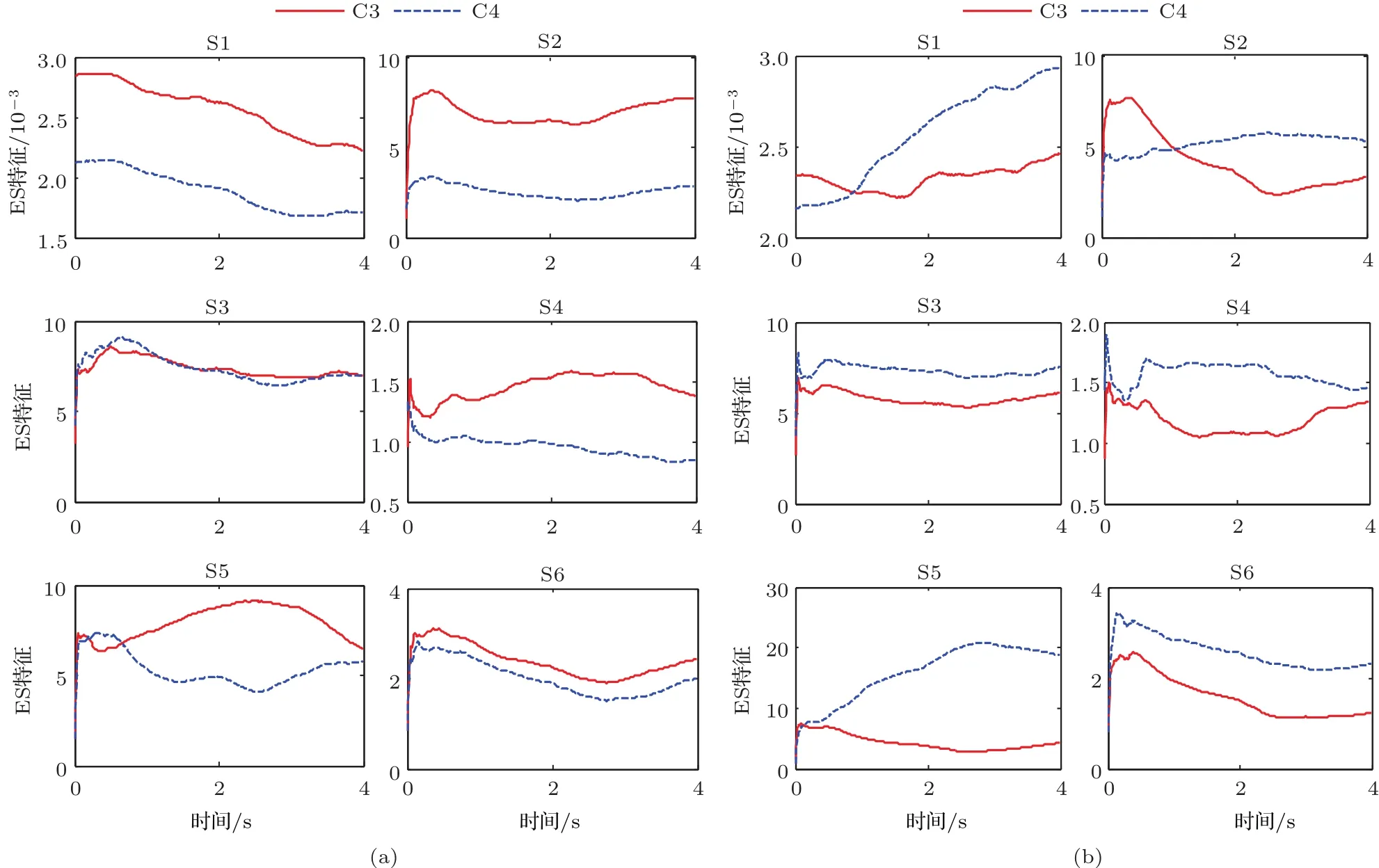
圖5 運動想象EEG ES特征 (a)左手運動想象;(b)右手運動想象Fig.5.ES features of motor imagery EEG:(a)Left motor imagery;(b)right motor imagery.

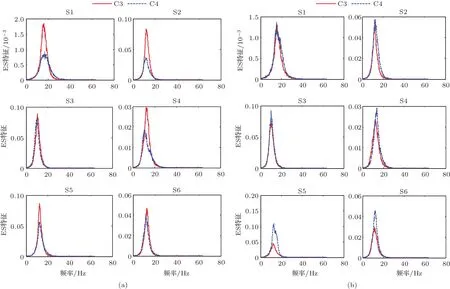
圖6 運動想象EEG MS特征 (a)左手運動想象;(b)右手運動想象Fig.6.MS features of motor imagery EEG:(a)Left motor imagery;(b)right motor imagery.

4.3 分類結果與對比

為了驗證本文方法的有效性,分別使用另外4種組合方法對兩組運動想象腦電數據進行特征提取和分類.組合方法如表1所列,本文分別使用方法1和2對3—5 s,4—6 s和5—7 s三個不同時間段的EEG信號進行分類識別.其中,方法1和方法2將計算得到的特征進行重采樣(128—4 Hz),從而得到了ELM的輸入特征向量;方法3是對3—7 s的EEG信號進行分類識別,該方法分別對ES特征和MS特征進行重采樣(128—4 Hz).最后,將兩種特征作為ELM的輸入特征向量;方法4中ELM輸入特征向量的獲取方法同本文方法(詳見第3節).

圖7(a)和圖7(b)分別是使用方法1和方法2得到的6名受試者在3個不同時間段的分類正確率.使用方法1時,受試者S1—S5的最優時段為4—6 s,受試者S6的最優時段為3—5 s;使用方法2時,受試者S4的最優時段為3—5 s,其他受試者的最優時段為4—6 s.在最優時段分類正確率的對比中,受試者S1和S6在方法1中有較高分類正確率,受試者S2—S5在方法2中有優勢.雖然在最優時段分類正確率的對比中,方法2優于方法1,但總體對比3個時間段的分類正確率可知,方法1優于方法2.在兩種方法的對比分析中可知,不同受試者對ES特征和MS特征的敏感度存在差異,圖7中顯示的正確率均為測試集的平均分類正確率.

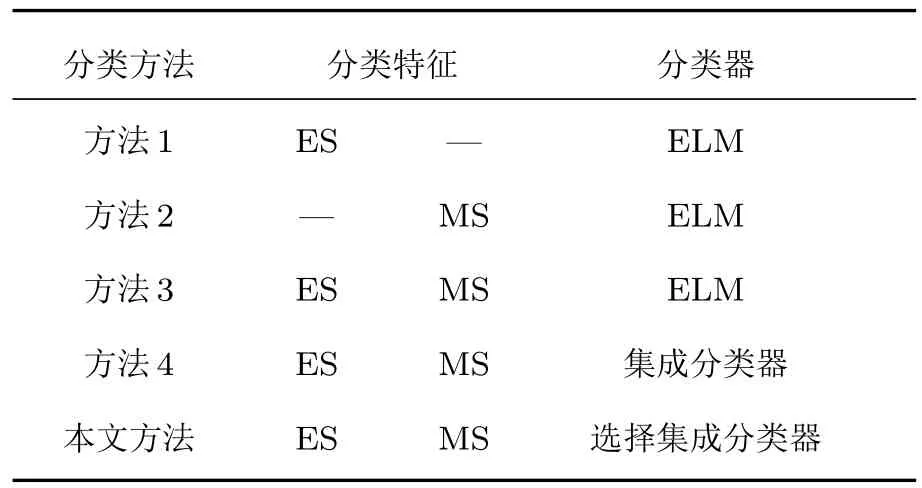
表1 不同方法的描述Table 1.Description of diff erent methods.

圖8對比了6名受試者在3—7 s運動想象中5種不同方法的測試集的平均分類正確率.由圖8可知,前3種方法各有優劣,后兩種方法較前3種方法有優勢,其中本文方法的分類正確率較前4種方法都高,有效證明了本文方法的有效性.同時,從圖8可知,圖中分類效果最好的為受試者S2,其平均分類正確率可達99.4%,分類效果較差的受試者為S3和S4,其平均分類正確率分別是77%和79.5%.

為了更好地驗證本文方法的有效性,本文不僅采用了識別率,同時使用受試者工作特征(receiver operating characteristic,ROC)曲線對分類模型性能進行評估,6名受試者的ROC曲線如圖9所示.從圖中可以比較明顯地看出,本文方法的ROC曲線下面積(area under the ROC curve,AUC)明顯大于其他方法,進一步驗證了本文方法的有效性.

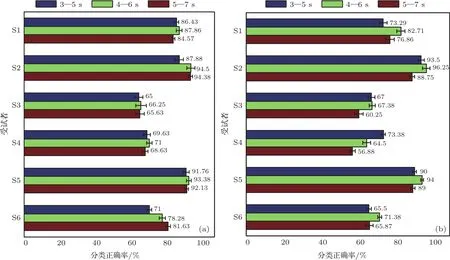
圖7 不同時段分類正確率的誤差條形圖 (a)方法1;(b)方法2Fig.7.Error bar chart of classifi cation accuracy with diff erent time:(a)Method 1;(b)method 2.

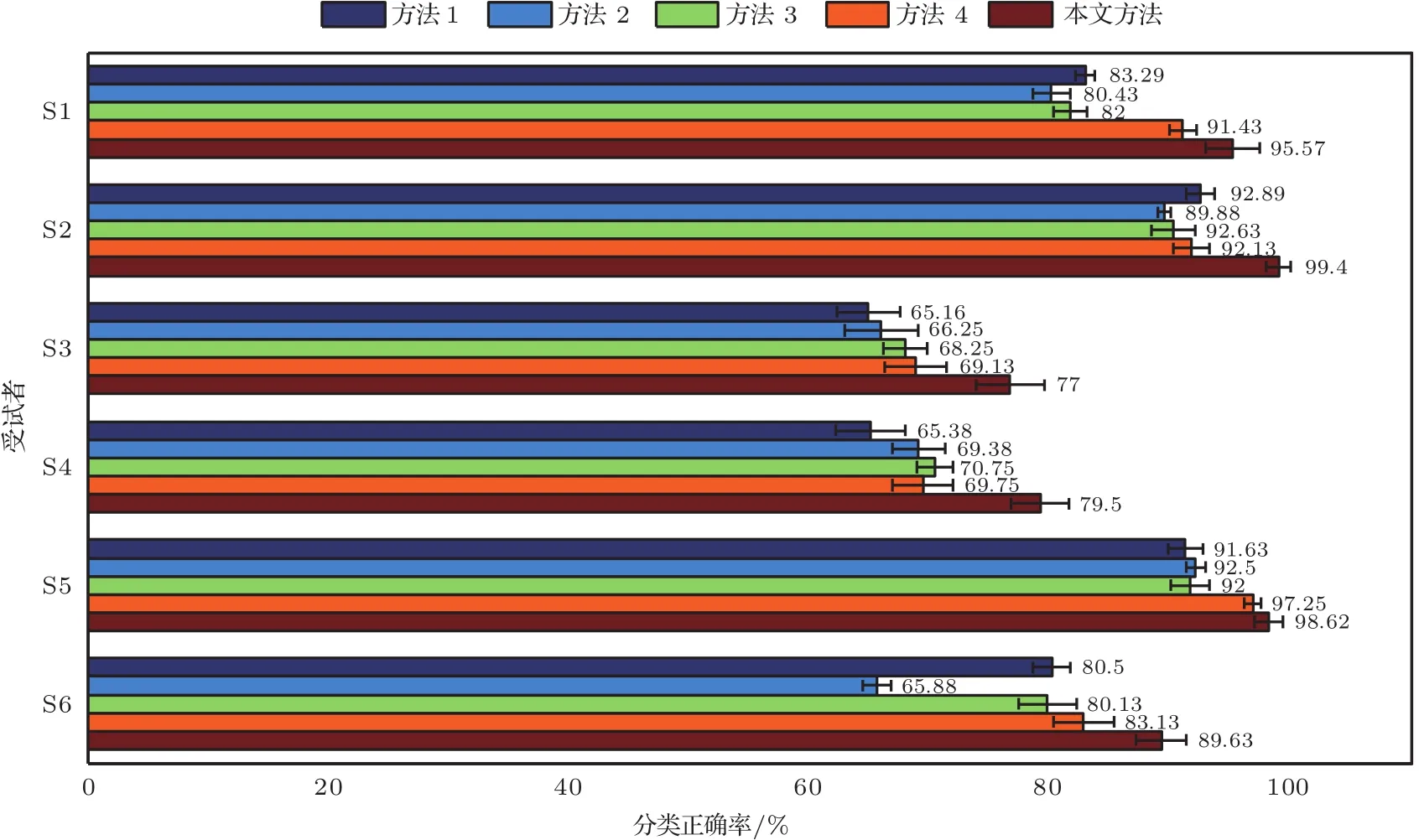
圖8 5種方法分類正確率的誤差條形圖Fig.8.Error bar chart of classifi cation accuracy with fi ve methods.

圖9 6名受試者在五種方法下對測試集分類生成的ROC曲線Fig.9.ROC curves generated by classifi cation of test sets by six subjects with fi ve methods.

5 討 論

如何提高具有非平穩性和非線性運動想象EEG信號的識別率是運動想象類腦機接口的關鍵之一.目前,研究者已經提出了很多運動想象腦電特征的提取方法,本文在前人研究的基礎上,提出了基于APEWT和選擇集成分類模型的運動想象模式識別方法.該方法從運動想象伴隨的ERD現象入手,根據不同時段和頻段特征的分類效果為其分配不同的權值,綜合考慮了多個時段和頻段的特征,從而避免了單一時段或頻段數據分析的不準確性和局限性.

圖5和圖6中兩種特征的分布情況符合ERD原理,這也再次證明了在運動想象期間發生了ERD這一現象.同時,從圖中可以明顯看出,受試者S3的ERD現象最不明顯,這可能是受試者S3的分類正確率最差的原因.

從圖7可以看出,不同時段和不同受試者有著不同的分類正確率.其中,大多受試者在4—6 s時間段內的識別率最高,可能是因為在3—5 s期間為運動想象執行的初始階段,受試者心理活動有一個滯后和適應的過程,在4—6 s期間,被試運動想象活動質量較好;6 s以后為運動想象執行的最后時間,被試者的運動想象心理活動質量有所下降,分類正確率相對較低.從圖7也可看出,不同的受試者可能會有著不同的的最優時段,不同的受試者對ES和MS兩種特征的敏感程度也不同,由此可知,如果將兩種特征進行有效融合,可能將有效提高分類效果.

由圖8可知,在最優時段中,方法2較方法1有優勢,在相同分類器情況下,MS特征比ES特征具有更好的分類效果.方法3雖然使用了ES特征和MS特征,但其分類效果并不理想,主要原因可能是沒有選擇最優時段的ES特征和最優頻段的MS特征,其特征向量中含有太多不相關特征影響了其分類正確率.

由圖9可知,本文方法和方法4的AUC值明顯大于方法3.同時從方法3,4和本文方法分類正確率的對比中可以發現,在相同特征情況下,集成分類器優于ELM,選擇集成分類器要優于非選擇集成分類器,主要原因可能是:1)在集成分類器中,考慮了EEG信號不同時段ES特征和頻段MS特征的差異性,并根據其不同的訓練效果為其分配相應的權重,有效降低了較差特征對分類結果的影響;2)相比非選擇集成分類器,選擇集成分類器剔除了分類性能較差的基分類器,提高了分類模型的識別率,從而得到了較好的分類效果.

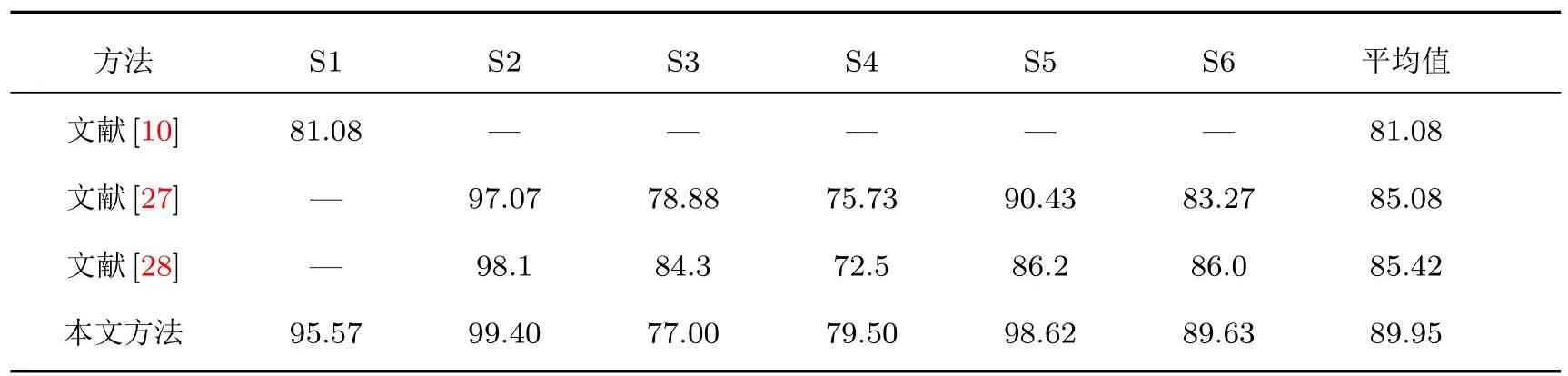
表2 不同受試者的平均正確率/%Table 2.Average accuracy of diff erent subjects/%.

此外,為進一步驗證本文方法的有效性,還將本文方法所得正確率與使用相同數據集的近期文獻進行了對比.文獻[10]使用HHT對5.5—7.5 s的EEG信號進行分解,綜合考慮了ES特征和AR模型系數;文獻[27]應用了FBCSP(fi lter bank common spatial pattern)算法提取了3—7.5 s運動想象的特征,沒有在FBCSP中執行特征選擇,而是使用了隨機森林分類器;文獻[28]使用了相應頻帶的Hjorth參數特征,表2中的正確率分別發生在5—6 s,7.5—8.5 s,5.5—6.5 s,6—7 s和5—6 s.表2比較了本文方法與這些文獻的平均分類正確率,受試者S1的平均分類正確率比文獻[10]提高了14.49個百分點,且高于BCI競賽中第一名的89.29%,后5名受試者的平均分類正確率為88.83%,比文獻[27]高出3.75個百分點,比文獻[28]高出3.41個百分點.本文方法在受試者S1,S2,S4,S5和S6的識別率都有所提高,進一步驗證了本文方法有效性和普適性.

表3為單次運動想象分類過程的時耗,實驗中,單次特征提取的時間為3—7 s.本文方法中時耗最長的是APEWT過程,本文方法的總時耗為0.2997 s,表明本文方法具有較好的實時性,適合在線BCI.

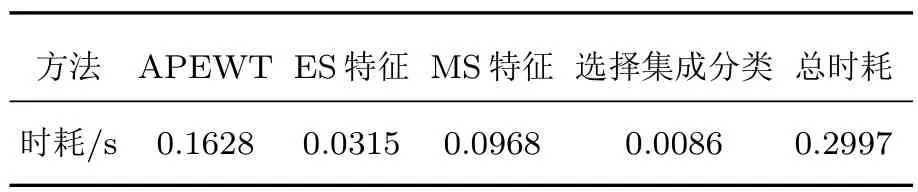
表3 本文方法的時耗統計Table 3.Time consumption of the method used in proposed method.

6 結 論

應用APEWT方法對EEG信號進行分解,使用最優模態重構后的信號得到ES特征,使用最優模態分量得到MS特征,通過加窗方法獲得了不同時段的ES特征和不同頻段的MS特征.根據不同時段和頻段特征的分類效果為其分配不同的權重,通過構建的選擇集成分類模型得到了較好的分類結果,其分類模型具有較好的分類性能和泛化能力.實驗中6名受試者的平均分類正確率為89.95%,單次運動想象分類過程的總時耗為0.2997 s,其平均分類正確率與近期其他文獻相比有明顯優勢,有效驗證了本文方法的有效性,為以后在線運動想象類BCI提供了新的方法.在本文基礎上,下一步的研究計劃是進一步完善本文方法并將其應用到實際的在線BCI中.

[1]Zhang D,Li J W 2017 Sci.Technol.Rev.35 62(in Chinese)[張丹,李佳蔚 2017科技導報 35 62]

[2]Gao S,Wang Y,Gao X,Hong B 2014 Trans.Biomed.Eng.61 1436

[3]Abdulkader S N,Atia A,Mostafa M S M 2015 Egy.Inf.J.16 213

[4]Fang X L,Jiang Z L 2007 Acta Phys.Sin.56 7330(in Chinese)[方小玲,姜宗來 2007物理學報 56 7330]

[5]Pfurtscheller G,da Silva F H L 1999 Cli.Neurophysiol.110 1842

[6]Lei M,Meng G,Zhang W M,Nilanjan S 2016 Acta Phys.Sin.65 108701(in Chinese)[雷敏,孟光,張文明,Nilanjan Sarkar 2016物理學報65 108701]

[7]Lei M,Meng G,Zhang W M,Joshua W,Nilanjan S 2016 Entropy 18 412

[8]Wang Y,Hou F Z,Dai J F,Liu X F,Li J,Wang J 2014 Acta Phys.Sin.63 218701(in Chinese)[王瑩,侯鳳貞,戴加飛,劉新峰,李錦,王俊2014物理學報63 218701]

[9]Xu B,Song A 2008 J.Biomed.Sci.Eng.1 64

[10]Sun H W,Fu Y F,Xiong X,Yang J,Liu C W,Yu Z T 2015 Acta Automatica Sin.41 1686(in Chinese)[孫會文,伏云發,熊馨,楊俊,劉傳偉,余正濤 2015自動化學報41 1686]

[11]Xie P,Chen X L,Su Y P,Liang Z H,Li X L 2013 Chin.J.Biomed.Eng.32 641(in Chinese)[謝平,陳曉玲,蘇玉萍,梁振虎,李小俚2013中國生物醫學工程學報32 641]

[12]Yang M H,Chen W Z,Li M Y 2017 Acta Automatica Sin.43 743(in Chinese)[楊默涵,陳萬忠,李明陽2017自動化學報43 743]

[13]Wu L Y,Lu H,Gao N,Wang T 2017 Chin.J.Biomed.Eng.36 224(in Chinese)[吳林彥,魯昊,高諾,王濤 2017生物醫學工程研究36 224]

[14]Zhang X Q,Liang J 2013 Acta Phys.Sin.62 050505(in Chinese)[張學清,梁軍 2013物理學報62 050505]

[15]Tang Z C,Sun S Q,Zhang K J 2017 Chin.J.Mech.Eng.53 60(in Chinese)[唐智川,孫守遷,張克俊2017機械工程學報53 60]

[16]Gilles J 2013 IEEE Trans.Signal Proc.61 3999

[17]Gilles J,Heal K 2014 Multiresol.Inf.Proces 12 1450044[18]Zheng J,Pan H,Yang S,Cheng J 2017 Signal.Proces 130 305

[19]Hou B W 2012 M.S.Dissertation(Xi’an:Xidian University)(in Chinese)侯秉文 2012碩士學位論文 (西安:西安電子科技大學)

[20]Zhao Y,Chen R,Liu W 2016 Comput.Sci.8 177(in Chinese)[趙宇,陳銳,劉蔚2016計算機科學 8 177]

[21]BCI Competition II http://www.bbci.de/competition/ii/[2018-1-15]

[22]BCI Competition IV http://www.bbci.de/competition/iv/[2018-1-15]

[23]Lindeberg T,ter Haar R B M 1994 Linear Scale-Space I:Basic Theory(Netherlands:Springer)pp1–38

[24]Cai Y P,Li A H,Wang T,Yao L,Xu P 2010 J.Vibra.Eng.4 430(in Chinese)[蔡艷平,李艾華,王濤,姚良,許平2010振動工程學報4 430]

[25]Huang G B,Zhu Q Y,Siew C K 2004 IEEE International Joint Conference on Neural Networks Proceedings Budapest,Hungary,July 25–29,2004 p985

[26]Huang G B,Zhu Q Y,Siew C K 2006 Neurocomput 70 489

[27]Bentlemsan M,Zemouri E T T,Bouchaff ra D,Yahya-Zoubir,B,Ferroudji,K 2014 5th International Conference on Intelligent Systems,Modelling and Simulation,Langkawi,Malaysia,Jan.27–29,2014 p235

[28]Suk H I,Lee S W 2013 Trans.Patt.Anal.Mach.Intelli 35 286