各向異性表面張力對定向凝固中共晶生長形態穩定性的影響?
徐小花 陳明文? 王自東
1 引 言
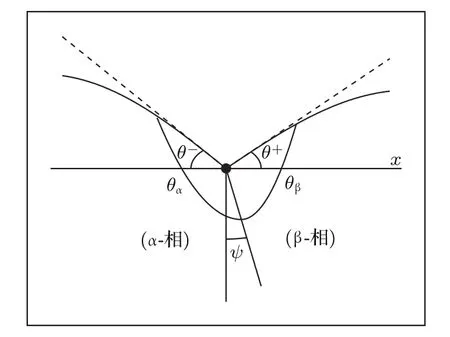
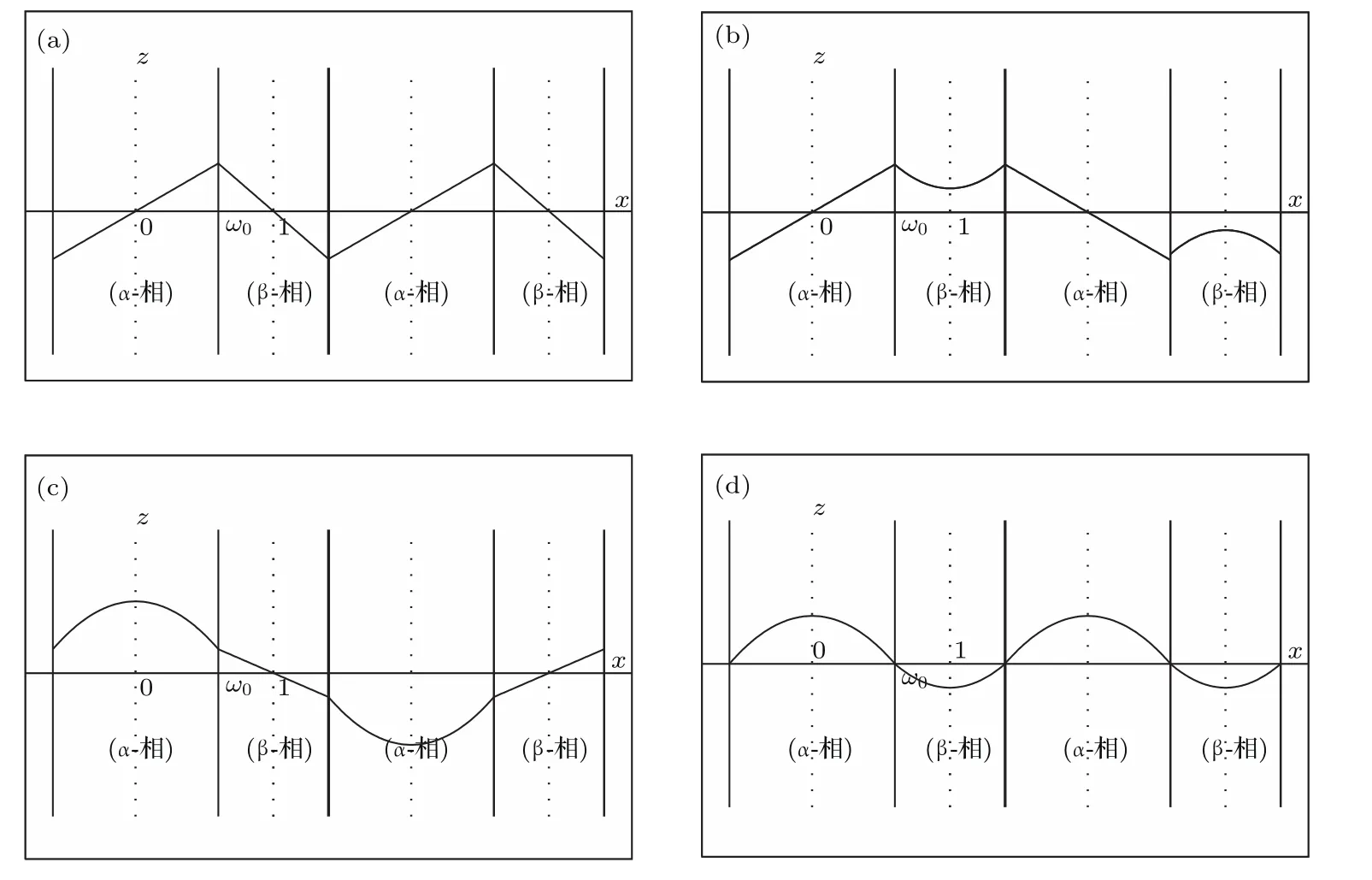
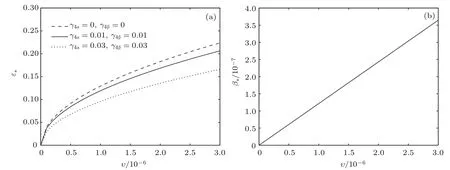
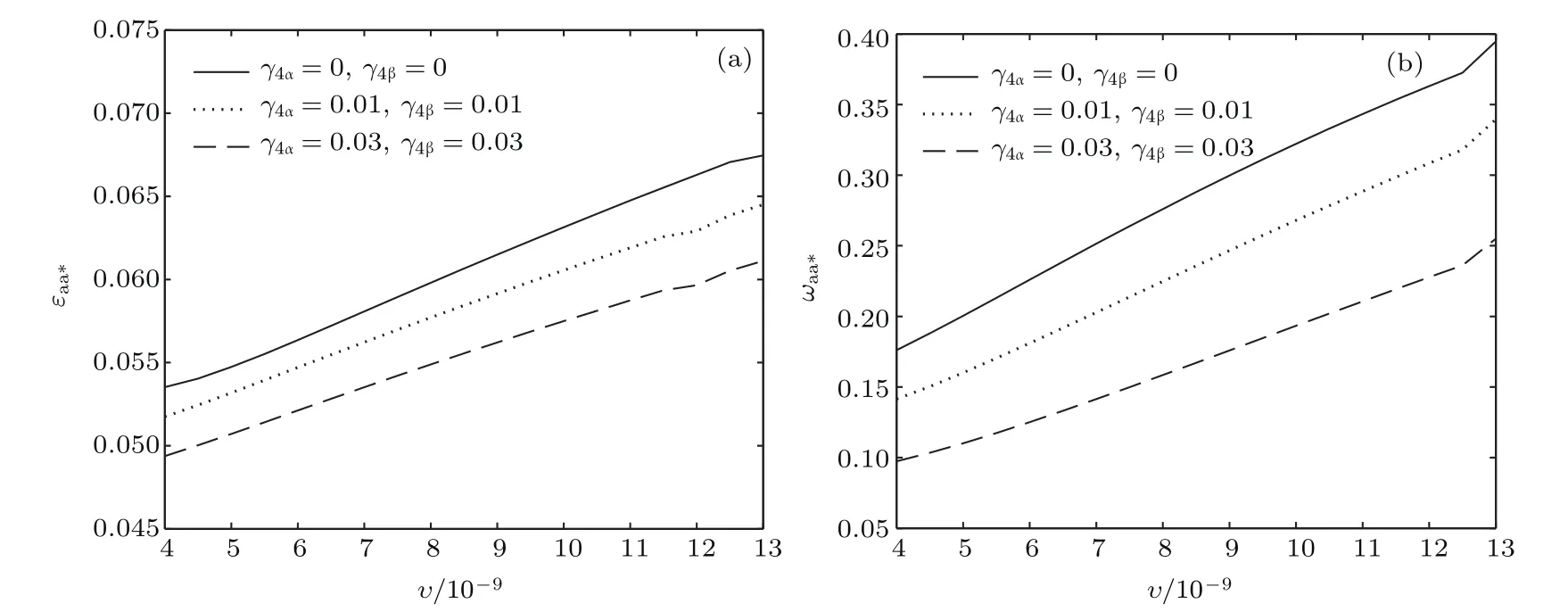
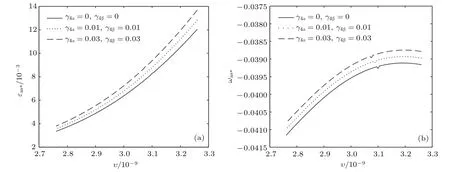
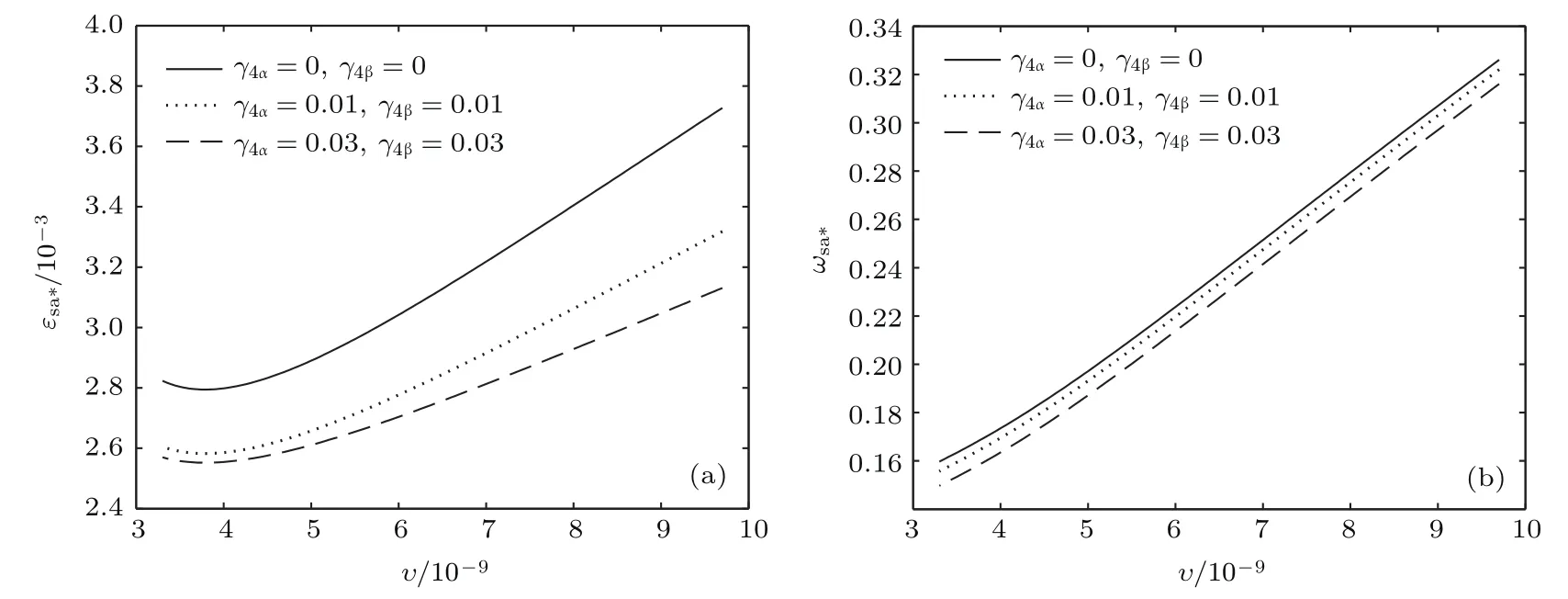
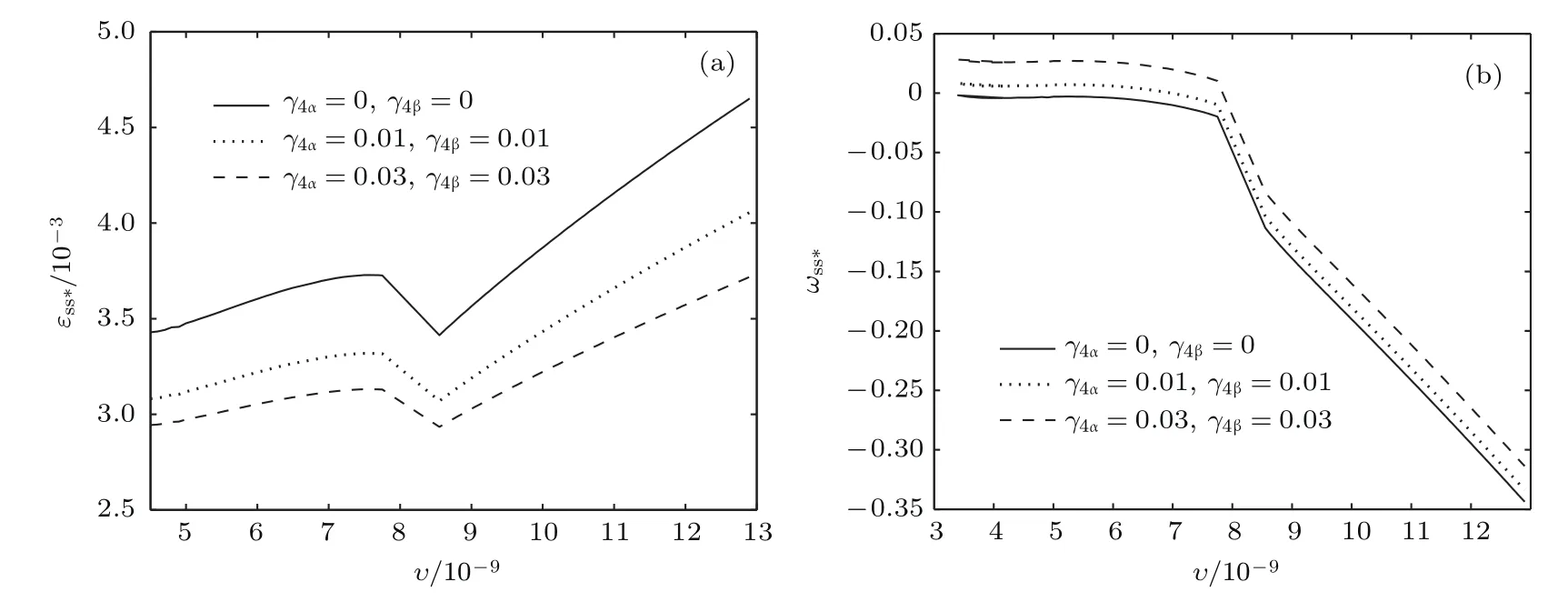
共晶界面形態穩定性是凝聚態物理學和材料科學的一個基礎課題[1?6].定向凝固過程中晶體形態的不穩定性可能會導致不同的微觀結構,最終極大地影響產品的物理和機械性能.Hele-Shaw生長室是觀察共晶定向凝固過程的典型實驗裝置,它是一個封存有樣品材料的十分扁平的容器.生長室設置了一個高溫區與一個低溫區,高溫區的溫度設為TH,低溫區的溫度為TC,材料的凝固溫度TM介于兩者之間:即TC 固體材料本身并非各向同性介質,其晶格結構使固體體內的物理量以及表面的物理參數依賴于取向,變為各向異性量.固體材料這些物理參量的各向異性特征對凝固過程動力學與界面穩定性機理以至對界面微結構圖案的形成與選擇造成重要的影響[14].王志軍等[15,16]研究了各向異性表面張力對定向凝固過程中初始平界面穩定性的影響,發現各向異性表面張力的非線性效應導致界面傾斜生長.Chen等[17]研究了各向異性表面張力對定向凝固過程中球晶生長的影響,發現在各向異性表面張力作用下,球晶生長初始階段部分界面首先向內移動,達到一定的熔化深度后向外移動.Xu[18]研究了各向異性表面張力對定向凝固過程中枝晶生長的影響,發現當存在各向異性表面張力時,枝晶系統具有兩種不同的整體不穩定性機理:震蕩不穩定性與低頻不穩定性.陳明文等[19]研究了各向異性表面張力對定向凝固過程中深胞晶生長的影響,發現當各向異性表面張力增大時,深胞晶界面全長增大,根部低端的曲率半徑增大.本文應用多重變量展開法研究各向異性表面張力條件下定向凝固共晶生長形態穩定性,揭示了各向異性表面張力對共晶生長不穩定性區域大小的影響. 圖1 共晶結構的示意圖Fig.1.Schematic diagram of the eutectic structure. 假設由α和β兩相組成的片層共晶以拉度V向液相穩定推進,共晶片層與固-液界面垂直.選取固-液界面處α相片層的中心為坐標原點,x軸與片層垂直,z軸與晶體生長方向平行,如圖1所示.共晶界面用函數z=h(x,t)表示,它也是共晶生長解的一部分. 本文引用Xu等[12]的無量綱化尺度,并且假設主間距的一半?w遠小于溶質擴散長度?D=κD/V,即?w? ?D,其中κD為溶質擴散系數. 選取?w為長度尺度,V為速度尺度,?w/V為時間尺度,?H/(cPρL)為溫度尺度,Ce為濃度尺度,其中?H是單位體積內固相潛熱,cP是比熱容,ρL是溶質密度,Ce是共晶濃度.無量綱溫度ˉT=(T?Te)/[?H/cPρL],無量綱濃度ˉC=(C?Ce)/Ce,無量綱無窮遠處濃度ˉC∞=[(C∞)D?Ce]/Ce,其中Te是共晶溫度,(C∞)D是有量綱無窮遠處濃度.為了書寫簡潔起見,下文省略掉無量綱量頭上的符號“-”.各向異性表面張力用四重對稱函數γ(θ)= γ0[1+ γ4cos(4θ)][14]表示,其中γ0為各向同性表面張力系數,γ4為各向異性表面張力系數,θ為界面法向量與z軸之間的夾角.共晶生長系統還包含以下無量綱量:Peclet數Pe= ?w/?D;形態參數M=(?mCe)/[?H/(cPρL)],m 是液相線系數;界面穩定性參數Γ = ?c/?w,?c是毛細長度,?c= γ0cPρLTe/(?H)2; 無量綱溫度梯度G=(G)D?w/[?H/(cPρL)],(G)D是與實驗裝置相關的有量綱溫度梯度;無量綱間距參數Wc=wc/?w,wc表示α相寬度的一半. 注意到γ0,γ4,m和分離系數κ都是分段常值函數,在α相和β相都有各自對應的常數值.用q來代表這類物理量,qα表示其在α相的函數值,qβ表示其在β相的函數值.由于溶質擴散長度?D遠小于熱擴散長度?T= κT/V,即?D? ?T,其中κT是熱擴散系數.界面溫度可以近似表示為TL=TS~ G(z?z?),其中TL,TS分別是液相和固相溫度,z?是與α相尖端位置有關的常數.對于典型的實驗材料,Peclet數Pe很小.以CBr4-C4Cl6[20,21]生長系統為例,Pe≈0.01,Γ≈2.5×10?5.為了做漸近分析,本文把Peclet數Pe作為基本的小參數,假設ε=Pe? 1且Γ=ε2ˉΓ,ˉΓ=O(1). 為考察共晶生長形態穩定性,利用共晶生長的定常解作為基態進行穩定性分析.在初始時刻t=0時對基態解做一小擾動,并將在t>0以后形成的非定常解分解成兩個部分: 其中{CB,hB}是系統的基態,{e C,?h}是系統的擾動態.假設初始擾動態的范數共晶生長系統的定常解為[11]: 其中 θ?是α相的接觸角,θ+是β相的接觸角,這兩個接觸角與夾度θα,θβ以及傾斜角ψ之間滿足關系式θ?= θα?π/2?ψ,θ+= θβ?π/2+ψ,如圖2所示. 圖2 三相點附近的界面示意圖Fig.2.A sketch of the interface shape near the triple point. 將系統方程以振幅遠小于1進行線性化處理,結合(1)式—(4)式,可以得到共晶生長系統的擾動態滿足以下控制方程和邊界條件: 1)在遠場區域,當z→∞時, 2)在側壁x=0和x=1上, (b)反對稱(antisymmetric)模式(A-模式) 3)在界面z=hB上, (a)Gibbs-Thomson條件 (a)對稱(symmetric)模式(S-模式) 由三角誘導公式可知, 于是有 結合(9)式和(10)式,Gibbs-Thomson條件可以改寫為 (b)雜質質量守恒條件 為了得到系統擾動態的漸近解,引入快變量[12] 按照多重變量(x,z,x+,z+,t+),解可以寫成如下形式: 并對波數函數和特征值做如下展開: 將(13)式—(17)式代入到方程和邊界條件(5)式—(12)式,可以得到系統在零級近似下的控制方程和邊界條件為 1)在遠場區域,當z→∞時, 2)在側壁x=0和x=1上, (a)S-模式 (b)A-模式 3)在界面z=0或z+=0上, (a)Gibbs-Thomson條件 (b)雜質質量守恒條件 其中?Θ(x)為分段常值函數,?Θα=1,?Θβ=??κ. 4)三相點處的連接條件,當x=w0時, 上述共晶生長系統有如下零級近似模式解[12]: 其中系數?D0是一個任意的復常數.記?A0(x)=?A0(x,0),將模式解(25)式和(26)式代入到界面條件(22)式和(23)式中,得到 該系統存在非零解的條件是方程的系數行列式為零,此條件給出了一個局部的色散關系式: 其中 局部色散關系式(29)是定向凝固中,對于平直界面情形的Mullins-Sekerka公式[22]的推廣.當γ4=0,ψ=0時,(29)式變為 (31)式與文獻[12]中給出的(10)式相同.對于任意給定的參數σ0,從色散關系式(29)中可以解出3個波函數: 其中 當γ4=0,ψ =0時,(32)式變為 其中 (33)式與Xu等[12]給出的(12)式相同. 這3個波函數{(x),(x),(x)}分別給出了系統3個基本的波動形式解{H1,H2,H3}.在這3個解中,波數函數(x)對應的波動形式解H2必須排除掉,因為當z+→∞時,濃度場的擾動振幅將指數增長,這是不合理的.有物理意義的解只有H1和H3.對于任意固定的點,在ε→0的極限條件下擾動態的一般解必定是解H1與解H3的線性迭加.從而,界面函數外部區域的通解可用這兩個基本界面行波的組合表示: 其中系數是待定常數. 濃度場滿足的一級近似控制方程和邊界條件為: 1)在遠場區域,當z→∞時, 2)在側壁x=0和x=1上, (a)S-模式 (b)A-模式 3)在界面z=0或z+=0上, (a)Gibbs-Thomson條件 (b)雜質質量守恒條件 上述濃度場的一級近似系統是非齊次的,它允許以下形式的模式解: 其中系數?D1是一個任意的復常數.記?A1(x)=?A1(x,0),將模式解(41)式和(42)式代入到界面條件(39)式和(40)中,整理得 其中 由于(43)式和(44)式構成的非齊次線性系統的系數行列式為零,故{?A1,?D1}存在非零解的充分必要條件為 (47)式給出了共晶生長系統的可解性條件: 從方程(43)式—(48)式得到如下公式: 為了得到全局模式解,界面函數的通解必須在三相點x=w0處滿足連接條件,在側壁x=0和x=1處滿足側壁條件.由于局部解在α相和β相是反對稱的(A-)或者是對稱的(S-),存在著四種不同的組合方式,因此共晶生長系統允許四種類型的全局模式解,即AA-,AS-,SA-和SS-模式,如圖3所示.在圖3(a)中,全局解在α相和β相均是反對稱的,稱之為AA-模式,即:當x=0時,?hα=0; 當x=1時,?hβ=0. 在圖3(b)中,全局解在α相是反對稱的,而在β相是對稱的,稱之為AS-模式,即: 當x=0時,?hα=0;當x=1時,??hβ/?x=0. 在圖3(c)中, 全局解在α相是對稱的,而在β相是反對稱的,稱之為SA-模式,即:當x=0時,??hα/?x=0;當x=1時,?hβ=0.在圖3(d)中,全局解在α相和β相均是對稱的,稱之為SS-模式,即: 當x=0時,??hα/?x=0;當x=1時,??hβ/?x=0. 1)全局AA-模式 全局解在三相點處滿足連接條件,在側壁上滿足側壁條件: 圖3 擾動系統的四種振動模式 (a)AA-模式;(b)AS-模式;(c)SA-模式;(d)SS-模式Fig.3.Sketch of the perturbed system by four vibration systems connected with a mass:(a)AA-modes;(b)AS-modes;(c)SA-modes;(d)SS-modes. 將解(34)式代入到方程(50)式和(51)式中,常數滿足以下方程組: 從方程組(52)—(55),得到 其中 對于全局AA-模式,特征值σ0滿足以下量子化條件: 其中Ξ =(cosθ?/cosθ+)2. 2)全局AS-模式 全局解在三相點處滿足連接條件,在側壁上滿足側壁條件: 將解(34)式代入到方程(60)式和(61)式中,化簡整理后得 對于全局AS-模式,特征值σ0滿足以下量子化條件: 3)全局SA-模式 全局解在三相點處滿足連接條件,在側壁上滿足側壁條件: 將解(34)式代入到方程(65)式和(66)式中,化簡整理后得 對于全局SA-模式,特征值σ0滿足以下量子化條件: 4) 全局SS-模式 全局解在三相點處滿足連接條件,在側壁上滿足側壁條件: 將解(34)式代入到方程(70)式和(71)式中,化簡整理后得 對于全局SS-模式,特征值σ0滿足以下量子化條件: 由量子化條件可以看出特征值σ0是關于參數ε和γ4的隱函數.任意給定參數ε和γ4,可以得到一個復數值σ0. 為了更好地闡明生長條件對共晶生長系統的影響,引入無量綱參數[11,12]υ = ?c,αV/κD, 它反映拉速V 的大小;?β=??c,α(G)D/mαCe,它反映溫度梯度(G)D的大小.通過化簡可以知道,υ=ε3ˉΓα,?β=υG/M.本文采用與Xu[23]研究枝晶的形態穩定性相似的方法,對于四種震蕩模式得到各自對應的穩定臨界值εaa?, εas?, εsa?和εss?. 共晶生長系統穩定的選擇判據為: 當ε>ε?,min,共晶生長系統是不穩定的; 當ε6ε?,min,共晶生長系統是穩定的. 共晶生長系統穩定的選擇性條件為: 1)全局穩定模式 給定生長條件,令量子化條件(59)式、(64)式、(69)式和(74)式中特征值σ0=0,發現只有AA-模式允許一系列中性穩定曲線,這種非震蕩條件下的不穩定模式又被稱為ST-模式.ST-模式導致所謂的交換穩定性機理.從圖4可知,隨著各向異性表面張力系數增大,穩定臨界值ε?隨之減小.這就意味著,各向異性表面張力減小穩定性區域,使得交換穩定性機理更加穩定.當各向異性表面張力退化為各向同性表面張力時,即當γ4α=0,γ4β=0時,圖4(a)中虛線與Xu等[12]給出的圖5(a)中黑色實線一致,圖4(b)中實線與Xu等[12]給出的圖5(b)中紅色實線一致.對比圖4(a)中三條曲線,各向異性表面張力對片層共晶穩定性有顯著的影響. 2)全局震蕩模式 給定生長條件,令量子化條件(59)式、(64)式、(69)式和(74)式中Re(σ0)=0,Im(σ0)= ω?=0,用數值的方法計算AA-,AS-,SA-和SS-模式對應的穩定臨界值εaa?, εas?, εsa? 和εss?. 這四種振蕩不穩定模式導致了所謂的全局不穩定性機理,圖5—圖8給出了四種震蕩不穩定模式的穩定臨界值εaa?, εas?, εsa? 和εss? 隨著υ 的變化圖. 從圖5、圖7和圖8可以看出,隨著各向異性表面張力系數增大,穩定臨界值εaa?,εsa? 和εss? 隨之減小. 這就意味著各向異性表面張力減小片層共晶生長的穩定性區域,增強了AA-,SA-和SS-這三種全局震蕩模式的全局不穩定性;然而,對于AS-全局震蕩模式而言,從圖6可以看出,隨著各向異性表面張力系數增大,穩定臨界值εas?隨之增大.這就意味著,各向異性表面張力增大片層共晶生長的穩定性區域,減弱了AS-全局震蕩模式的全局不穩定性. 圖4 當σ0=0(n=0)時,對于AA-模式,臨界值ε?隨υ的變化,其中?C∞=?0.12,w0=0.63,?=0.15,?κ=1.33,(R c=ˉΓβ/ˉΓα),Mα=0.107,Mβ=?0.0711,θ+=65.3?,θ?=59.5?,ψ=0,?β=4.88×10?10(a)臨界值ε?隨υ的變化;(b)參數β?隨υ的變化Fig.4.The variation ofε?withυfor the AA-mode when the eigenvalueσ0=0(n=0),where?C∞=?0.12,w0=0.63,?=0.15,?κ=1.33,(R c=ˉΓβ/ˉΓα),Mα=0.107,Mβ=?0.0711,θ+=65.3?,θ?=59.5?,?β=4.88×10?10:(a)The variation of the stability critical numberε? with υ;(b)the variation ofβ? with υ. 圖5 當Re(σ0)=0,Im(σ0)= ωaa?時,對于AA-模式,(a)臨界值εaa?隨υ的變化,(b)特征頻率值ωaa?隨υ的變化,其他參數取值同圖4Fig.5.The variation of εaa? with υ for the AA-mode when the eigenvalue Re(σ0)=0,Im(σ0)= ωaa?:(a)The variation of the stability critical number εaa? with υ;(b)the variation of the corresponding eigenfrequency ωaa?withυ.The values of other parameters are the same as those given in Fig.4. 圖6 當Re(σ0)=0,Im(σ0)=ωas?時,對于AS-模式,(a)臨界值εas?隨υ的變化,(b)特征頻率值ωas?隨υ的變化,其他參數取值同圖4Fig.6.The variation of εas? with υ for the AS-mode when the eigenvalue Re(σ0)=0,Im(σ0)= ωas?:(a)The variation of the stability critical number εas? with υ;(b)the variation of the corresponding eigenfrequency ωas?withυ.The values of other parameters are the same as those given in Fig.4. 圖7 當Re(σ0)=0,Im(σ0)=ωsa?時,對于SA-模式,(a)臨界值εsa?隨υ的變化,(b)特征頻率值ωsa?隨υ的變化,其他參數取值同圖4Fig.7.The variation of εsa? with υ for the SA-mode when the eigenvalue Re(σ0)=0,Im(σ0)= ωsa?:(a)The variation of the stability critical number εsa? with υ;(b)the variation of the corresponding eigenfrequency ωsa?withυ.The values of other parameters are the same as those given in Fig.4. 圖8 當Re(σ0)=0,Im(σ0)=ωss?時,對于SS-模式,(a)臨界值εss?隨υ的變化,(b)特征頻率值ωss?隨υ的變化,其他參數取值同圖4Fig.8.The variation of εss? with υ for the SS-mode when the eigenvalue Re(σ0)=0,Im(σ0)= ωss?:(a)The variation of the stability critical number εss? with υ;(b)the variation of the corresponding eigenfrequency ωss?withυ.The values of other parameters are the same as those given in Fig.4. 本文研究了定向凝固過程中各向異性表面張力對共晶生長形態穩定性的影響.應用多重變量漸近展開法解決了表面張力為各向異性時線性繞動態的特征值問題,導出了受各向異性表面張力影響的界面形態表達式和擾動振幅變化率與波數滿足的色散關系,以此為基礎給出了共晶生長的臨界穩定性判據和界面形態滿足的量子化條件.結果表明:各向異性表面張力對定向凝固系統的穩定性有顯著的影響.與各向同性表面張力條件下的共晶凝固系統相比較,考慮各向異性表面張力的定向凝固系統中共晶生長界面形態也有兩種整體不穩定機理:由非震蕩導致的“交換穩定性”和由震蕩導致的“整體波動不穩定性”機理.穩定性分析表明共晶界面穩定性取決于Peclet數的某一個臨界值ε?,當Peclet數大于臨界值ε?時,共晶界面形態不穩定;當Peclet數小于臨界值ε?時,共晶界面形態穩定.隨著各向異性表面張力增大,對應于AA-,SA-和SS-模式的臨界值εaa?,εas?,εsa? 和εss?減小,各向異性表面張力減小穩定性區域,各向異性表面張力加強這三種模式的穩定性;然而,隨著各向異性表面張力增大,對應于AS-模式的臨界值εas?也增大,各向異性表面張力增大穩定性區域,各向異性表面張力減弱AS-模式的穩定性. 本文得到了加拿大麥吉爾大學徐鑒君教授的指導與幫助,作者表示感謝.作者徐小花感謝天津城建大學陳永強教授的有益討論與幫助. [1]Jackson K A,Hunt J D 1966 Trans.Metall.Soc.AIME 236 1129 [2]Trivedi R,Mangnin P,Kurz W 1987 Acta Metall.35 971 [3]Liu J M,Zhou Y H,Shang B L 1990 Acta Metall.Mater.38 1625 [4]Kassner K,Misbah C 1991 Phys.Rev.A 44 6533 [5]Li X,Ren Z M,Fautrelle Y,Zhang Y D,Esling C 2010 Acta Mater.58 1403 [6]Meng G H,Lin X,Huang W D 2007 J.Mater.Sci.Technol.23 851 [7]Karma A,Sarkissian A 1996 Metall.Mater.Trans.A 27 635 [8]Parisi A,Plapp M 2008 Acta Mater.56 1348 [9]Ginibre M,Akamatsu S,Faivre G 1997 Phys.Rev.E 56 780 [10]Datye V,Langer J S 1981 Phys.Rev.B 24 4155 [11]Xu J J,Li X M,Chen Y Q 2014 J.Cryst.Growth 401 93 [12]Xu J J,Chen Y Q,Li X M 2014 J.Cryst.Growth 401 99 [13]Xu J J 2017 Interfacial Wave Theory of Pattern Formation in Solidifi cation: Dendrites,Fingers,Cells and Free Boundaries(2nd Ed.)(New York:Springer)pp503–572 [14]Xu J J 2006 Introduction to kinetics of solidifi cation and stability theory of the interface(Beijing:Science Press)pp33–44(in Chinese)[徐鑒君 2006凝固過程動力學與交界面穩定性理論導引(北京:科學出版社)第33—44頁] [15]Wang Z J,Wang J C,Yang G C 2008 Acta Phys.Sin.57 1246(in Chinese)[王志軍,王錦程,楊根倉 2008物理學報57 1246] [16]Wang Z J,Wang J C,Yang G C 2010 Chin.Phys.B 19 017305 [17]Chen M W,Wang Z D,Xu J J 2014 J.Cryst.Growth 385 115 [18]Xu J J 1991 Physica D 51 579 [19]Chen M W,Chen Y C,Zhang W L,Liu X M,Wang Z D 2014 Acta Phys.Sin.63 038101(in Chinese)[陳明文,陳奕臣,張文龍,劉秀敏,王自東2014物理學報63 038101] [20]Seetharaman V,Trivedi R 1988 Metall.Trans.A 19 2955 [21]Mergy J,Faivre G,Guthmann C,Mellet R 1993 J.Cryst.Growth 134 353 [22]Mullins W W,Sekerka R F 1964 J.Appl.Phys.35 444 [23]Xu J J 2002 J.Cryst.Growth 245 134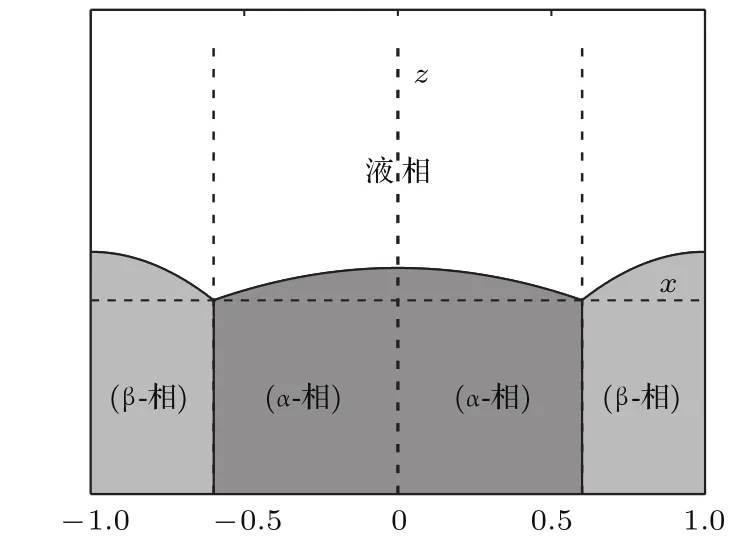
2 定向凝固系統的數學模型
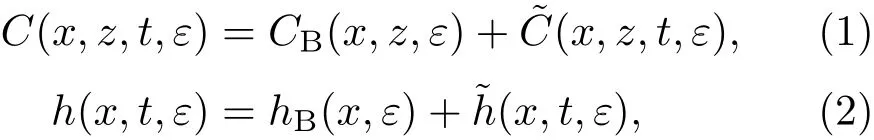
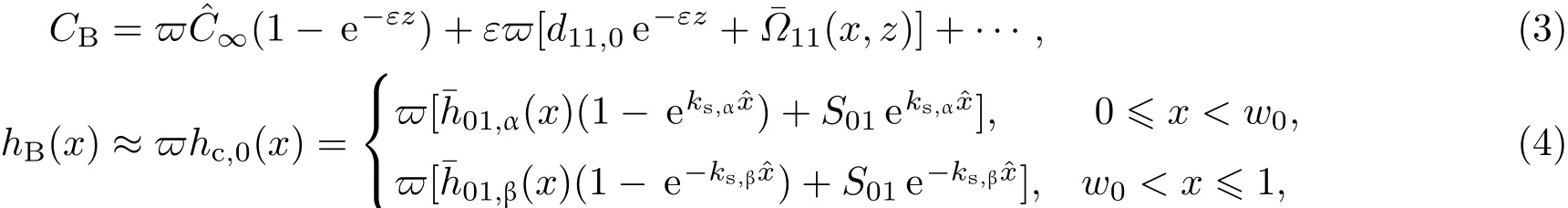
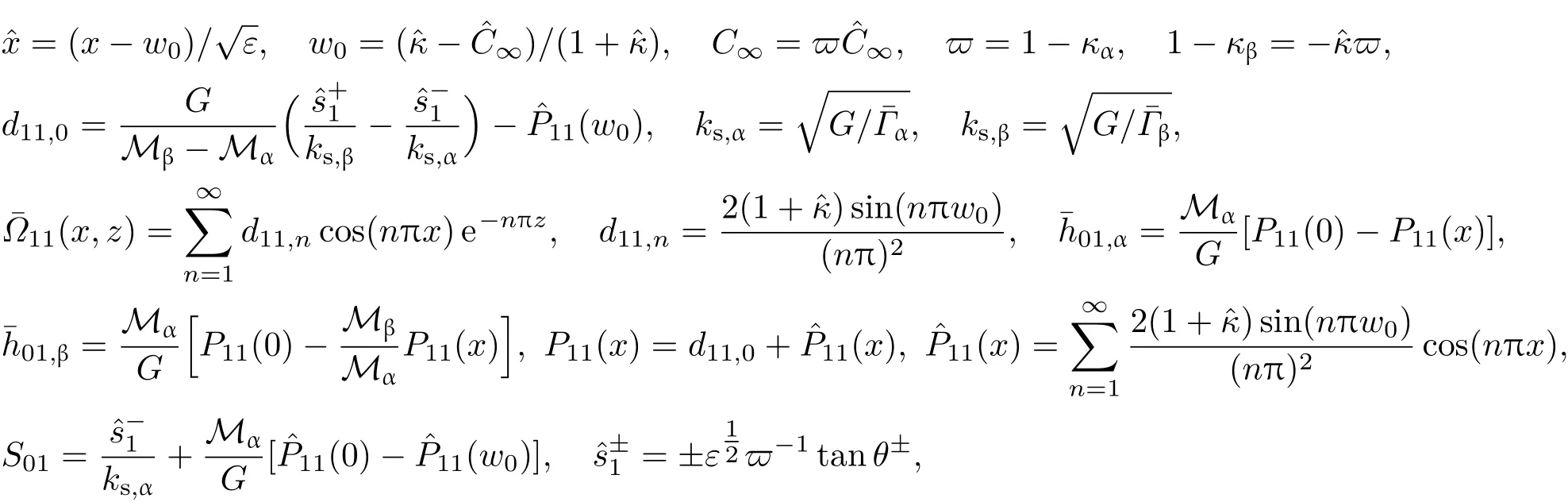
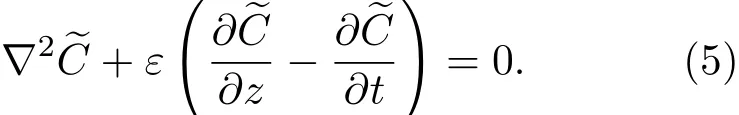

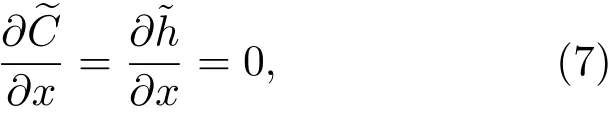

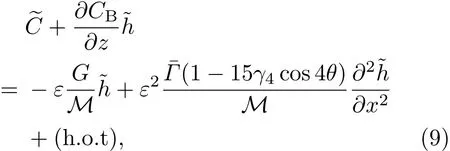
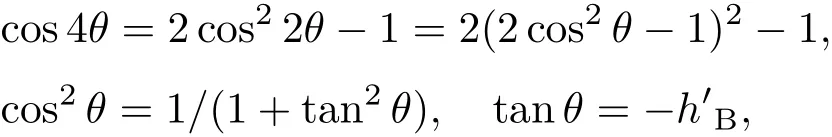
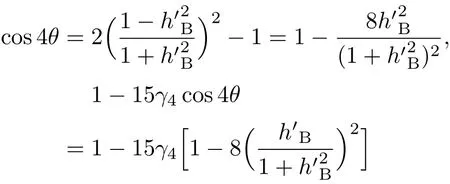
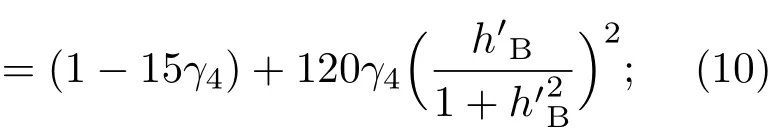
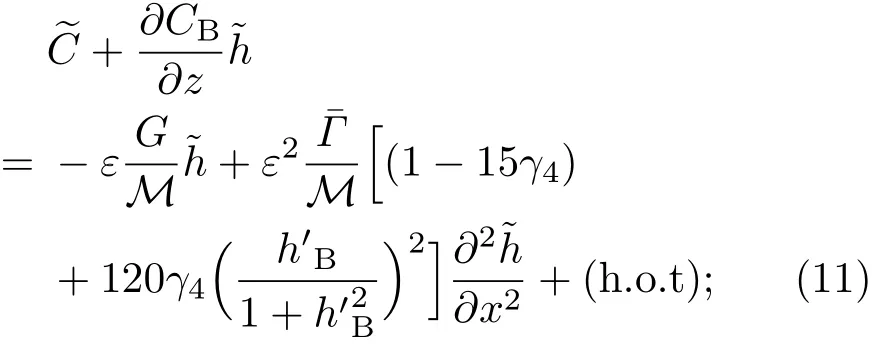
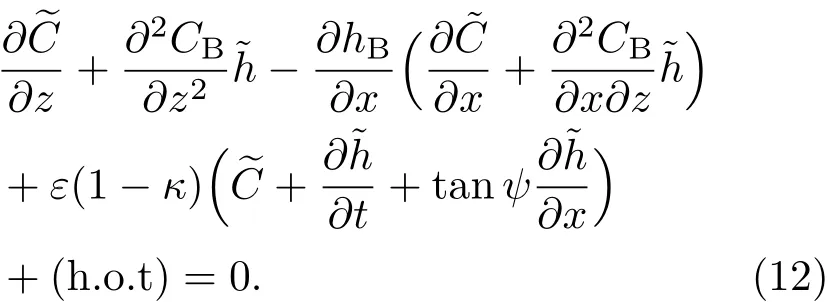
3 擾動態的多重變量漸近展開解
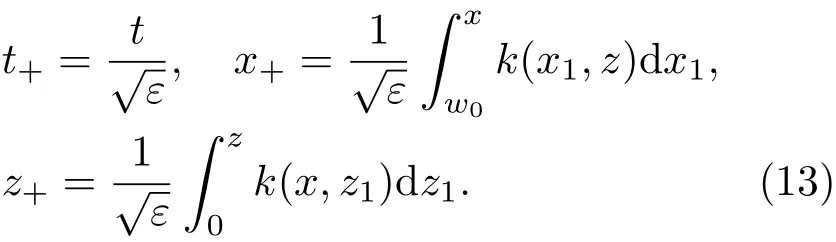
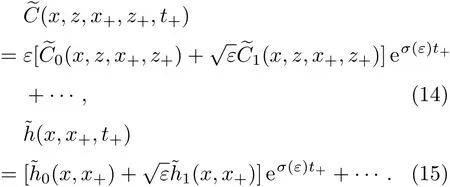
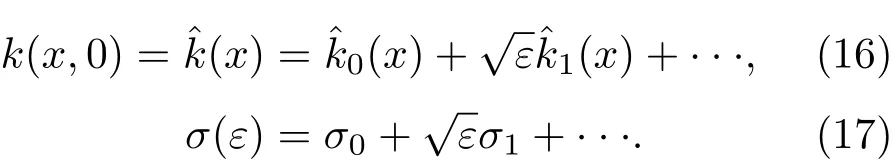
3.1 零級近似解
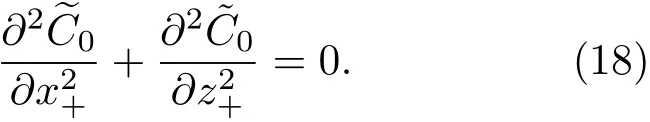



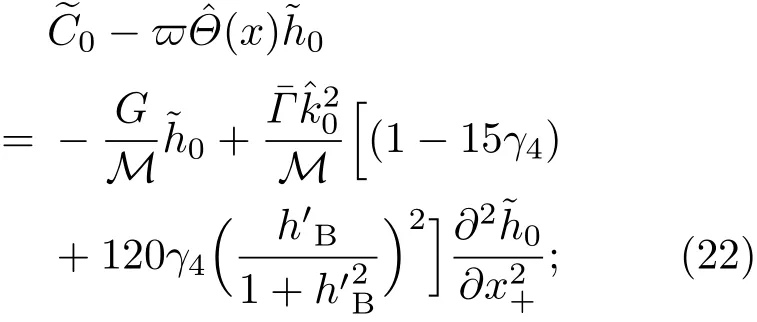
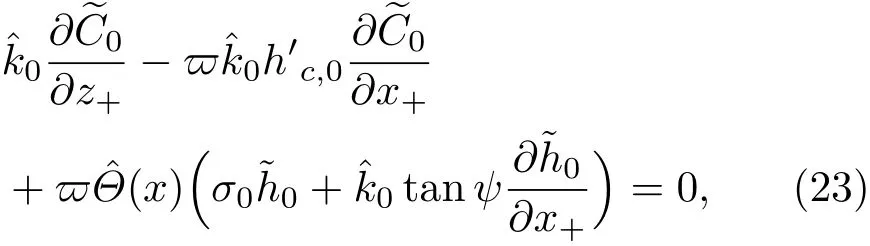
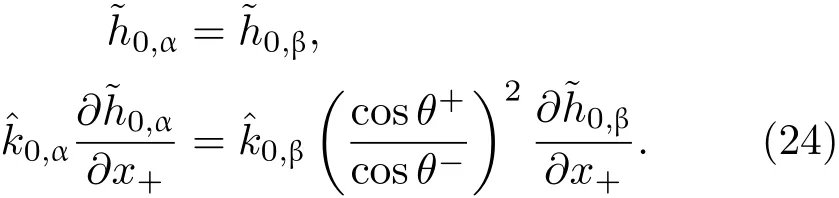
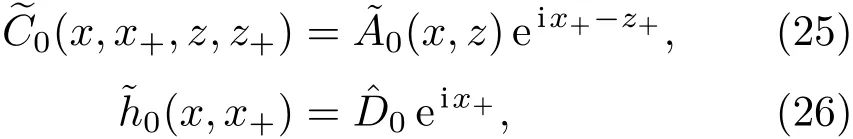
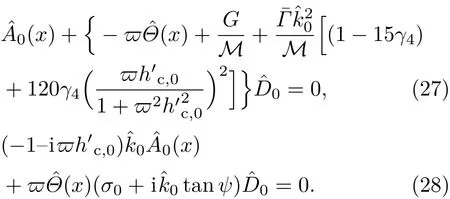
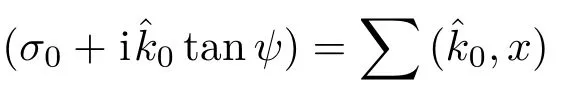
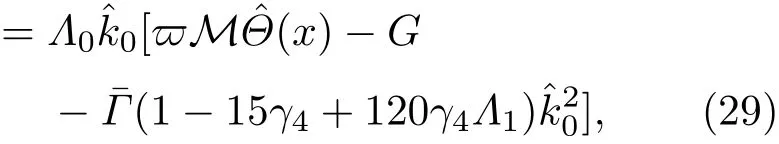
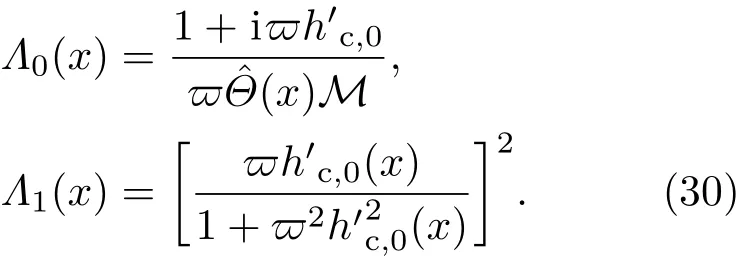
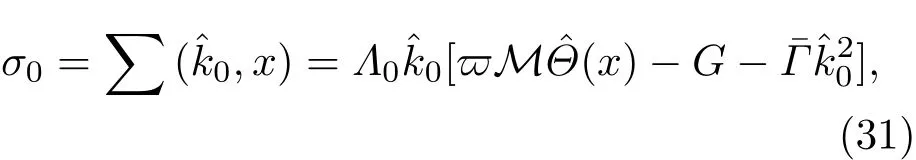
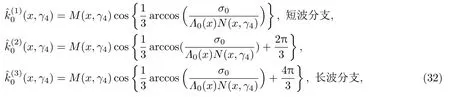
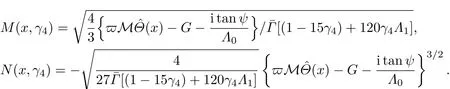
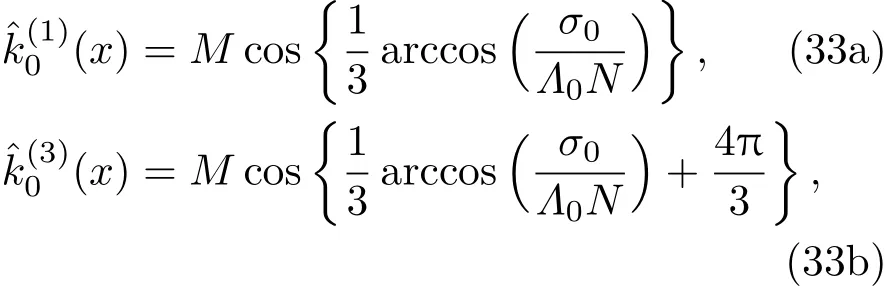

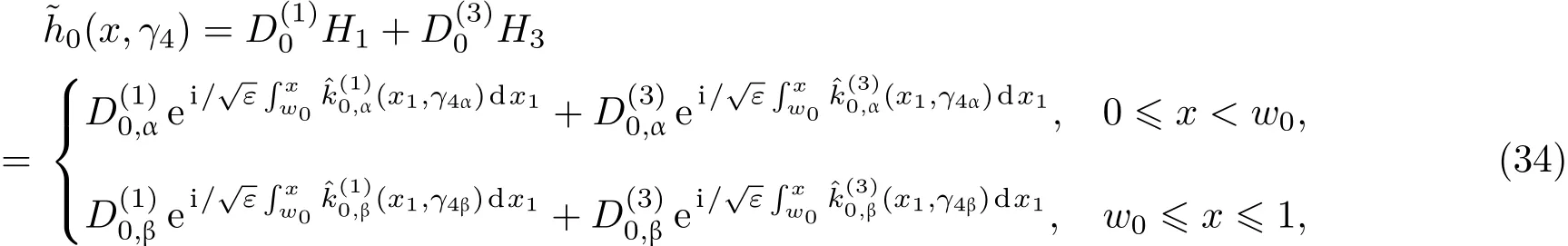
3.2 一級近似解
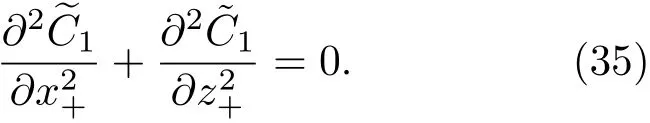

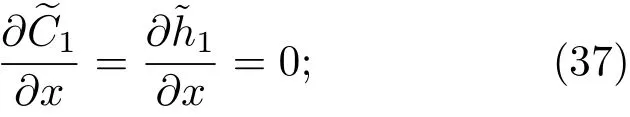

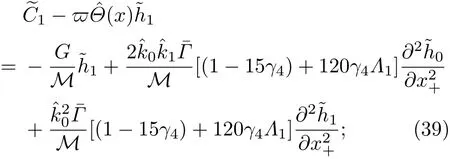
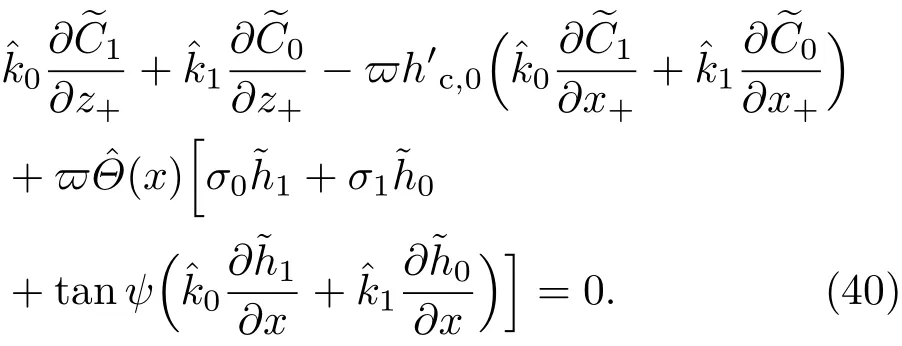
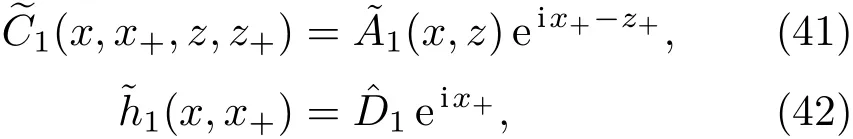
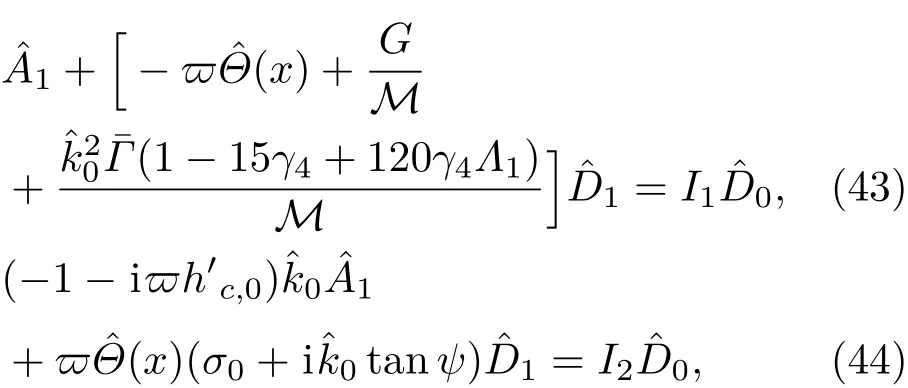
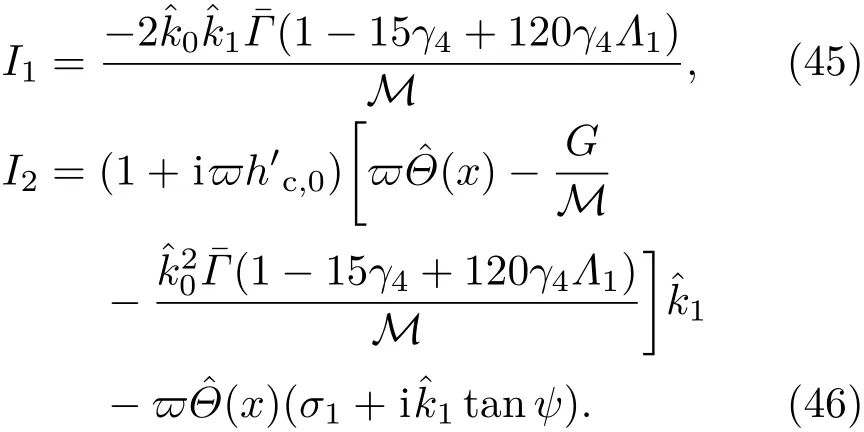
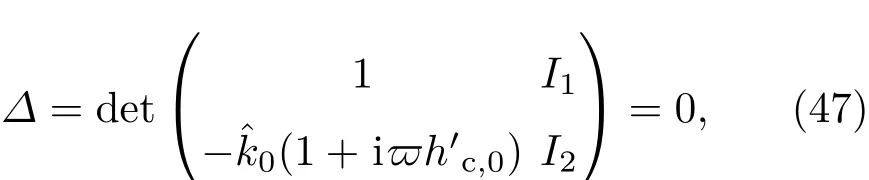
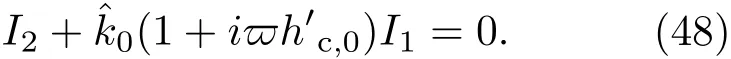
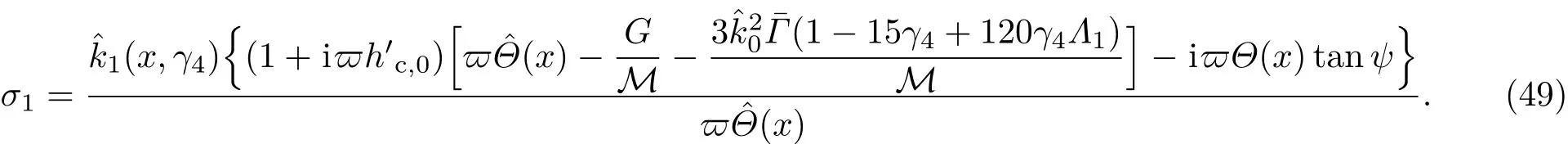
4 全局模式解和量子化條件
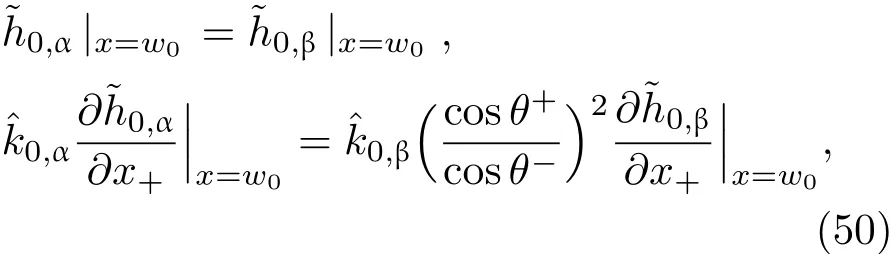
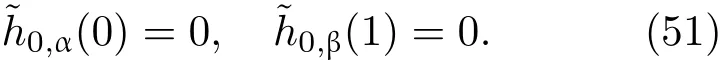
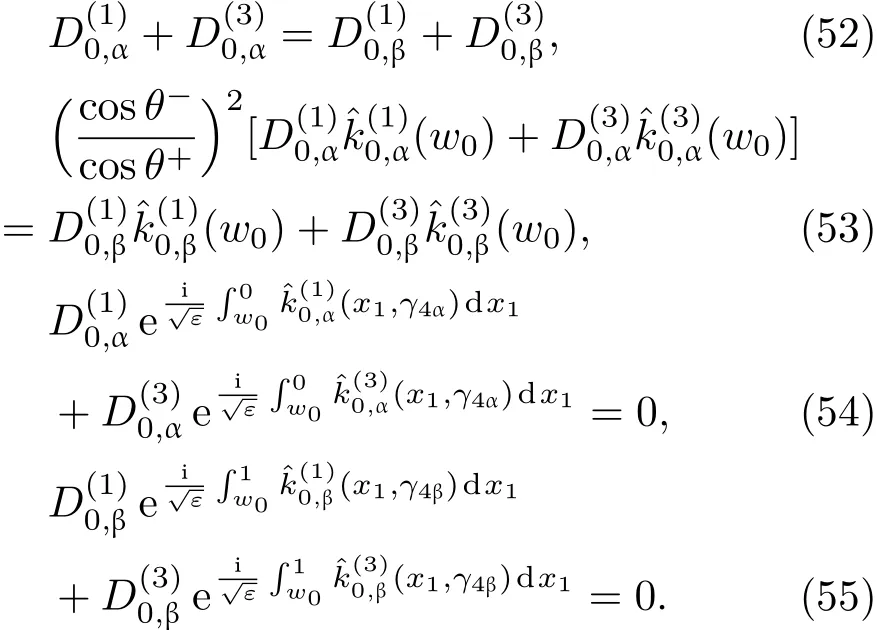
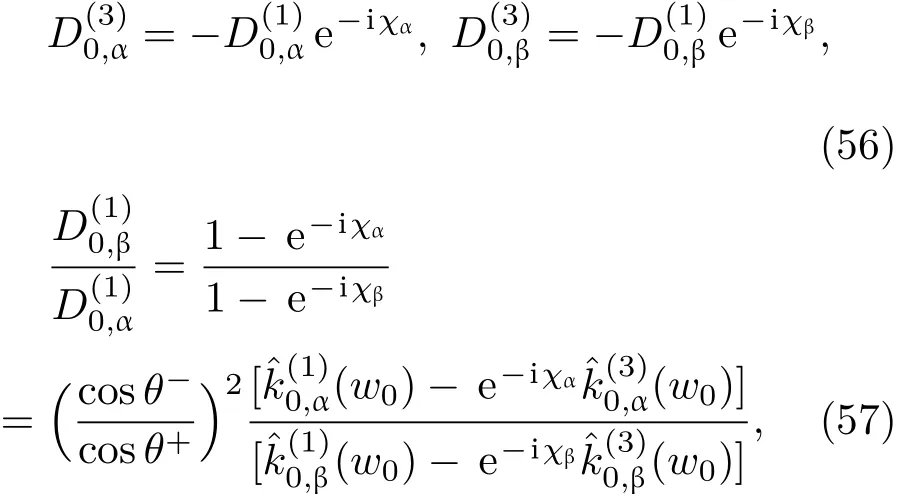
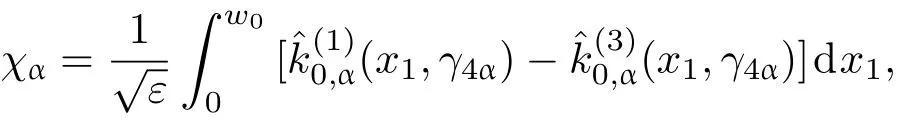
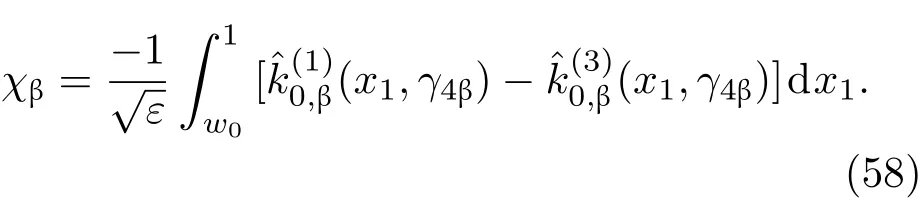
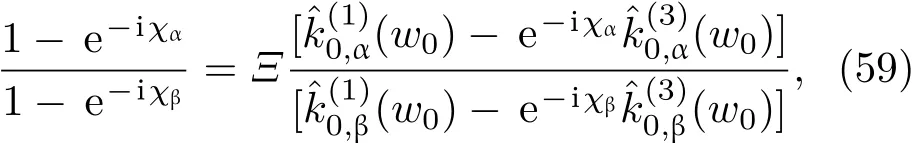
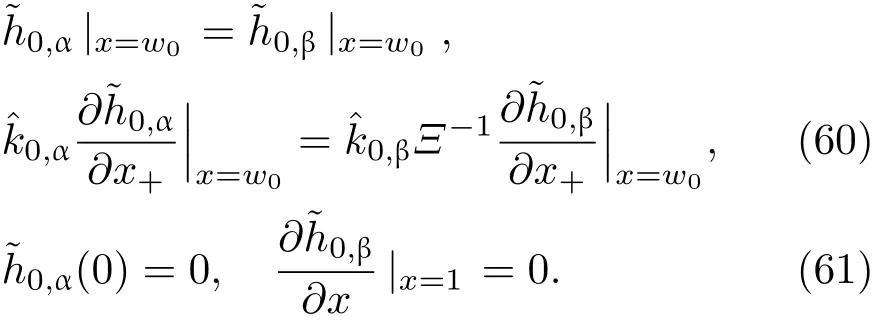
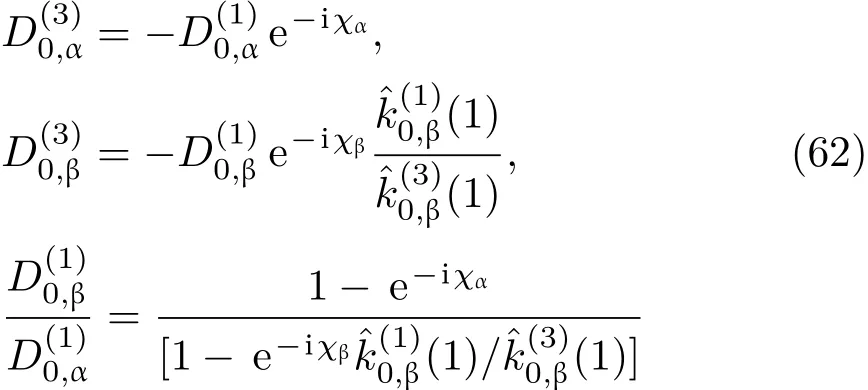
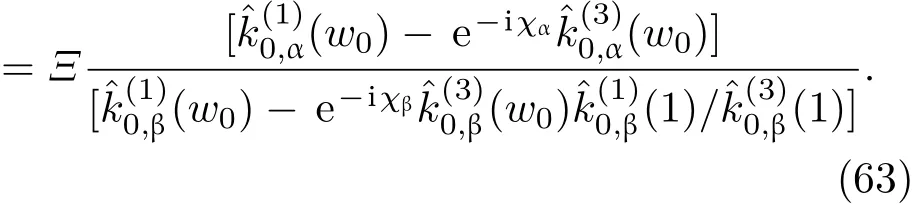
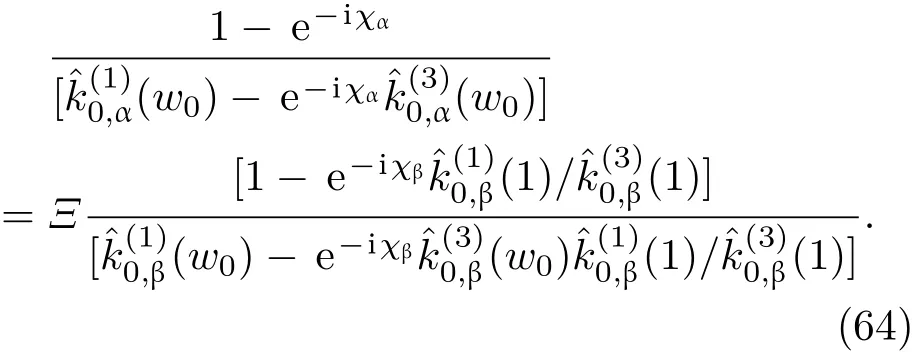
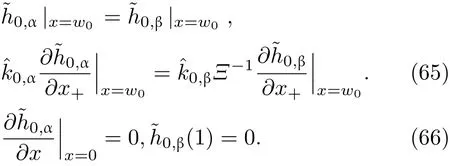
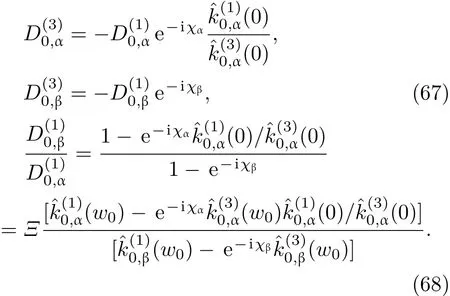
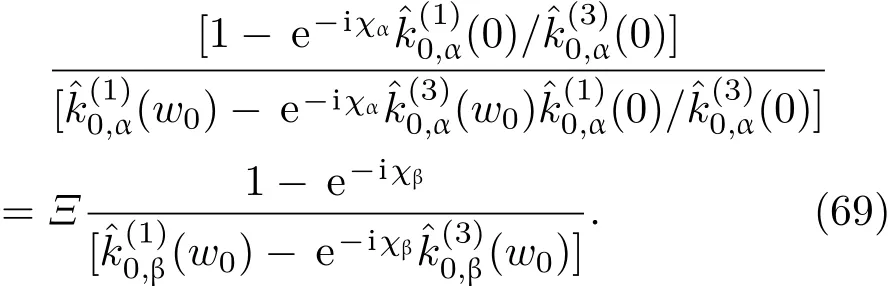
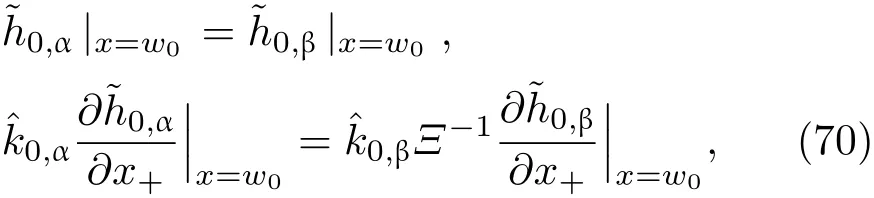

5 穩定性分析
6 結 論

