軸流壓氣機(jī)考慮展向摻混的數(shù)值計(jì)算

李 濤 ，吳亞?wèn)| ，2，歐陽(yáng)華 ，3

（上海交通大學(xué)機(jī)械與動(dòng)力工程學(xué)院1燃?xì)廨啓C(jī)研究院2：上海200240；3.先進(jìn)航空發(fā)動(dòng)機(jī)協(xié)同創(chuàng)新中心，北京100083）

0 引言

軸流壓氣機(jī)是航空發(fā)動(dòng)機(jī)與燃?xì)廨啓C(jī)3大核心部件之一，準(zhǔn)確、快速、完整地獲得其整體性能指標(biāo)和各排葉片的展向參數(shù)分布，是其氣動(dòng)設(shè)計(jì)的基礎(chǔ)。葉輪機(jī)械內(nèi)部3元流動(dòng)分析方法始于吳仲華教授20世紀(jì)50年代提出的2類相對(duì)流面理論，并在50～70年代經(jīng)歷了快速發(fā)展，積累了大量有關(guān)氣動(dòng)損失、落后角、堵塞因子的模型和經(jīng)驗(yàn)關(guān)聯(lián)式，逐漸成為葉輪機(jī)械性能分析的主要工具。1990年以來(lái)CFD技術(shù)快速發(fā)展，但其計(jì)算模型、計(jì)算成本和計(jì)算精度都仍有很大的提升空間，且較多應(yīng)用于壓氣機(jī)氣動(dòng)設(shè)計(jì)的正問(wèn)題，以及局部流場(chǎng)的優(yōu)化。在壓氣機(jī)氣動(dòng)設(shè)計(jì)領(lǐng)域，流線曲率法依然是初始反問(wèn)題計(jì)算和優(yōu)化的主要工具。軸流壓氣機(jī)的氣動(dòng)設(shè)計(jì)一直向著更高的級(jí)負(fù)荷和更低的展弦比發(fā)展，這意味著級(jí)間通流的展向摻混作用更明顯，紊流強(qiáng)度增大，二次流動(dòng)增強(qiáng)。因此，在流線曲率法的計(jì)算中引入展向摻混模型有助于更加準(zhǔn)確地反映壓氣機(jī)的內(nèi)部流場(chǎng)的展向分布特性，提高計(jì)算精度。在計(jì)及展向摻混的分析研究領(lǐng)域，Adkins和Smith[1]認(rèn)為展向摻混由二次流決定；而Gallimore和Cumpsty[2-3]根據(jù)試驗(yàn)認(rèn)為小尺度的紊流擴(kuò)散起主導(dǎo)作用；Wisler[4]得到了更為全面而嚴(yán)謹(jǐn)?shù)慕Y(jié)論，認(rèn)為大尺度的二次流和小尺度的紊流在展向摻混過(guò)程中都起到重要作用，只是因壓氣機(jī)展向位置和運(yùn)行工況的變化而有不同的表現(xiàn)；通過(guò)對(duì)N-S方程進(jìn)行理論分析[5-7]，也可得到類似結(jié)論：對(duì)N-S方程進(jìn)行質(zhì)量加權(quán)的概率平均和周向平均，可得到S2流面基本方程組[5]。由運(yùn)動(dòng)方程可看出，影響S2流面動(dòng)量輸運(yùn)的有分子黏性應(yīng)力、紊流脈動(dòng)應(yīng)力和周向非均勻應(yīng)力，而周向非均勻應(yīng)力包括二次流在內(nèi)的3維大尺度因素。

基于上述分析，本文采用Wisler的觀點(diǎn)，在基本的S2通流計(jì)算中同時(shí)引入了紊流擴(kuò)散和二次流的模型，以評(píng)估展向摻混對(duì)流場(chǎng)的作用。將計(jì)算結(jié)果與公開發(fā)表的數(shù)據(jù)進(jìn)行對(duì)比和分析，表明考慮展向摻混后流線曲率法能較好地預(yù)測(cè)出壓氣機(jī)的流場(chǎng)特性。

1 數(shù)值方法

1.1 控制方程

在實(shí)際葉輪機(jī)械中，氣體的流動(dòng)是非定常、黏性、全3維的流動(dòng)。計(jì)算過(guò)程中作定常、絕熱和軸對(duì)稱的假設(shè)，在葉片排前后緣及葉片通道內(nèi)部均設(shè)置計(jì)算站，基于N-S方程推導(dǎo)出流線曲率法在S2流面上的控制方程，分別是沿流線方向和沿計(jì)算站方向的速度梯度方程、流量連續(xù)方程及焓方程[8]。

對(duì)于給定各葉片排出氣角分布的反問(wèn)題，注意到環(huán)量與出氣角的關(guān)系

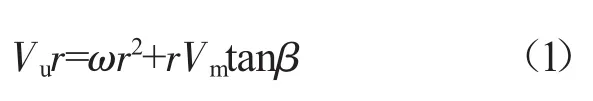
在跨聲流動(dòng)中，為得到子午Ma＜1而相對(duì)Ma＞1的超聲速解，可通過(guò)式（1）將正問(wèn)題轉(zhuǎn)化為反問(wèn)題迭代求解。所以上述方法可用于相對(duì)跨聲流動(dòng)問(wèn)題。

1.2 紊流擴(kuò)散模型

紊流擴(kuò)散采用G-C模型，該模型表達(dá)的物理過(guò)程是因紊流擴(kuò)散導(dǎo)致的動(dòng)量和熱量的展向摻混，并用渦黏系數(shù)μt和紊流熱傳導(dǎo)系數(shù)kt來(lái)度量。μt通過(guò)摻混系數(shù)ε確定，kt和μt通過(guò)紊流Prandtl數(shù)相關(guān)聯(lián)

摻混系數(shù)ε可由軸向速度Vz、軸向級(jí)長(zhǎng)度Lz和雷諾數(shù)確定

實(shí)際計(jì)算中Lz可取進(jìn)口葉片軸向平均長(zhǎng)度，和Re的值可通過(guò)經(jīng)驗(yàn)給出，進(jìn)而確定渦黏系數(shù)及紊流熱傳導(dǎo)系數(shù)[9-10]。

計(jì)及摻混作用時(shí)，作用于切向面和軸向面上的應(yīng)力忽略不計(jì)，計(jì)算方程組的黏性應(yīng)力項(xiàng)也需有所變動(dòng)，徑向、切向、軸向分量分別為

問(wèn)卷包括三個(gè)部分，主要調(diào)查學(xué)生對(duì)各項(xiàng)英語(yǔ)技能的自我評(píng)價(jià)、學(xué)習(xí)難度評(píng)價(jià)以及提高各項(xiàng)技能的愿望，均為單項(xiàng)選擇題，選項(xiàng)為五級(jí)量表形式(1=很差/很難/很不愿意、2=差/難/不愿意、3=一般/無(wú)所謂、4=好/容易/愿意、5=很好/很容易/很愿意)。

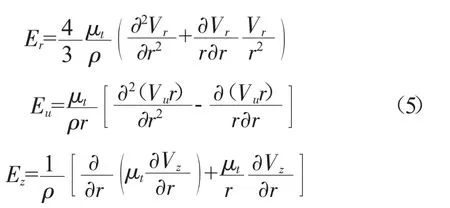
黏性耗散項(xiàng)為

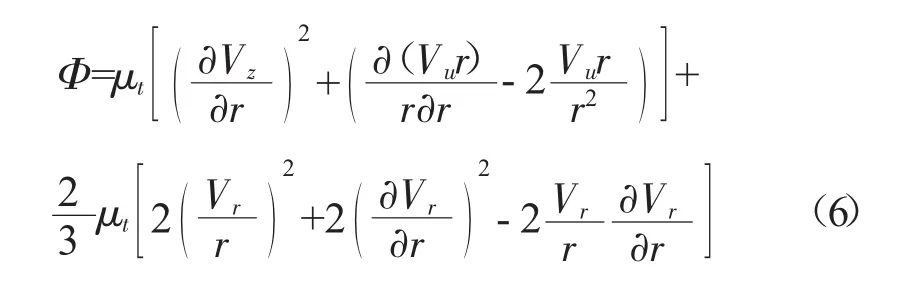
1.3 落后角計(jì)算及修正

二次流的作用通過(guò)落后角來(lái)體現(xiàn)。在正問(wèn)題中需要采用合適的模型預(yù)估落后角的分布。目前已經(jīng)有多種落后角預(yù)估模型，有些方法要求已知流場(chǎng)的若干氣動(dòng)參數(shù)，需要進(jìn)行迭代計(jì)算。2維Carter公式是計(jì)算落后角的經(jīng)典公式，僅根據(jù)葉型的幾何參數(shù)就可初步得到落后角的分布。這里根據(jù)文獻(xiàn)[11]采用Carter公式的另一種形式

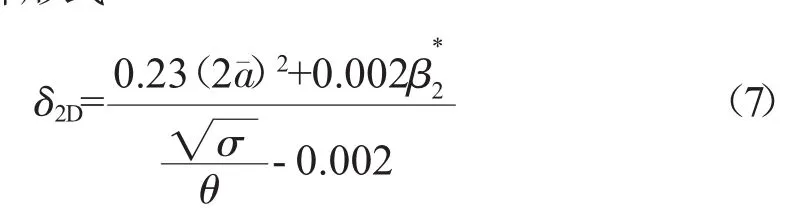
式中為葉型最大厚度沿弦長(zhǎng)的相對(duì)位置，計(jì)算中取0.5即可得到較為滿意的結(jié)果。

修正落后角可應(yīng)用Roberts[12-13]的方法。該模型基于NASA壓氣機(jī)中間級(jí)的試驗(yàn)數(shù)據(jù)，以2維Carter公式為基礎(chǔ)表達(dá)了3維流動(dòng)對(duì)落后角的影響。葉柵通道內(nèi)的流體受到旋轉(zhuǎn)的影響，在離心作用下產(chǎn)生向頂部流動(dòng)的趨勢(shì)。低能流體在頂部的聚集，會(huì)因間隙的存在進(jìn)一步影響流動(dòng)。因此，Roberts認(rèn)為轉(zhuǎn)子的落后角在葉根處表現(xiàn)為過(guò)轉(zhuǎn)折，而在葉尖處表現(xiàn)為欠轉(zhuǎn)折。靜子的流動(dòng)現(xiàn)象更加明顯，由于葉柵通道垂直氣流運(yùn)動(dòng)方向壓力梯度的存在，流體會(huì)在端部附近的區(qū)域形成2個(gè)大小相同、方向相反的二次流旋渦。這在落后角上就表現(xiàn)為欠轉(zhuǎn)折。對(duì)已有的數(shù)據(jù)進(jìn)行插值擬合后，要求在端壁處表現(xiàn)為過(guò)轉(zhuǎn)折。Roberts研究發(fā)現(xiàn)，靜子落后角與壁面邊界層厚度、葉型折轉(zhuǎn)角和稠度關(guān)系較大，轉(zhuǎn)子落后角與壁面邊界層厚度、葉頂間隙和展弦比關(guān)系較大。

Roberts的落后角修正模型在葉根處總是表現(xiàn)為過(guò)轉(zhuǎn)折，但事實(shí)上在葉根附近是存在欠轉(zhuǎn)折的，而且Roberts建立模型使用的數(shù)據(jù)也能明顯反映這一現(xiàn)象，但是其最終模型并沒有體現(xiàn)這一點(diǎn)[14]。動(dòng)葉內(nèi)的流體受離心力的影響有向頂部流動(dòng)的趨勢(shì)，但其葉根處仍然會(huì)有二次流渦團(tuán)的存在。本文在研究中對(duì)轉(zhuǎn)子葉根處取2°～4°的欠轉(zhuǎn)折，然后計(jì)算分析其他參數(shù)，對(duì)各修正點(diǎn)重新進(jìn)行插值擬合，得到改善后的落后角展向分布結(jié)果。

2 計(jì)算結(jié)果與分析

壓氣機(jī)3S1是PW公司的試驗(yàn)壓氣機(jī)，是1臺(tái)3級(jí)低速壓氣機(jī)，展弦比為0.81，輪轂比為0.915，設(shè)計(jì)轉(zhuǎn)速為5455 r/min，設(shè)計(jì)壓比為1.357，設(shè)計(jì)流量為4.3 kg/s。輪轂和機(jī)匣均為圓柱形狀，流道沒有收斂。文中采用的試驗(yàn)數(shù)據(jù)來(lái)自文獻(xiàn)[15]和[16]，與流線曲率法的計(jì)算結(jié)果進(jìn)行對(duì)比。本算例從輪轂到機(jī)匣選定11條流線，各排葉片前后緣分別設(shè)置計(jì)算站，每排葉片通道內(nèi)設(shè)置3個(gè)計(jì)算站，上下游各設(shè)置5個(gè)計(jì)算站，共43個(gè)計(jì)算站。具體的計(jì)算網(wǎng)格如圖1所示。圖中每個(gè)格點(diǎn)代表1個(gè)計(jì)算站，水平方向格點(diǎn)相連代表流線。

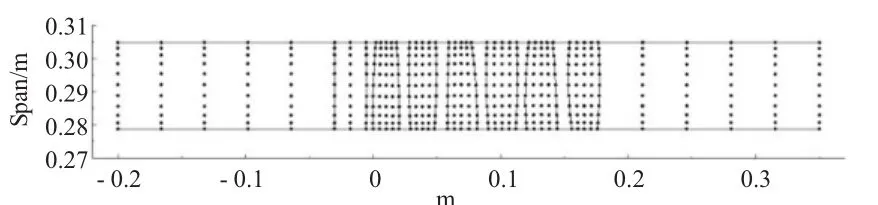
圖1 方案（4）的計(jì)算網(wǎng)格

（1）無(wú)黏無(wú)摻混，落后角由Carter公式給出。

（2）無(wú)黏無(wú)摻混，落后角由Carter公式經(jīng)Roberts修正給出。

（3）G-C模型，落后角由Carter公式給出。

（4）G-C模型，落后角由Carter公式經(jīng)Roberts修正給出。

（5）文獻(xiàn)數(shù)據(jù)。

本文進(jìn)行了5種方案的計(jì)算。第3級(jí)轉(zhuǎn)子和靜子的出口氣流角計(jì)算結(jié)果與文獻(xiàn)給出的數(shù)據(jù)的對(duì)比如圖2、3所示。由于出口氣流角與落后角有直接關(guān)系，觀察到Carter公式和改善后的Roberts修正各自計(jì)算結(jié)果的準(zhǔn)確性。從圖2中可見，Roberts修正在轉(zhuǎn)子的葉尖附近取得了很好的效果，與文獻(xiàn)數(shù)值基本重合，同時(shí)葉根處欠轉(zhuǎn)折的趨勢(shì)也明顯與文獻(xiàn)數(shù)據(jù)相符，但是幅度上偏小。從圖3中可見，Roberts修正使靜子兩端部的流動(dòng)計(jì)算均取得明顯改善，展向分布形態(tài)更接近文獻(xiàn)數(shù)據(jù)。

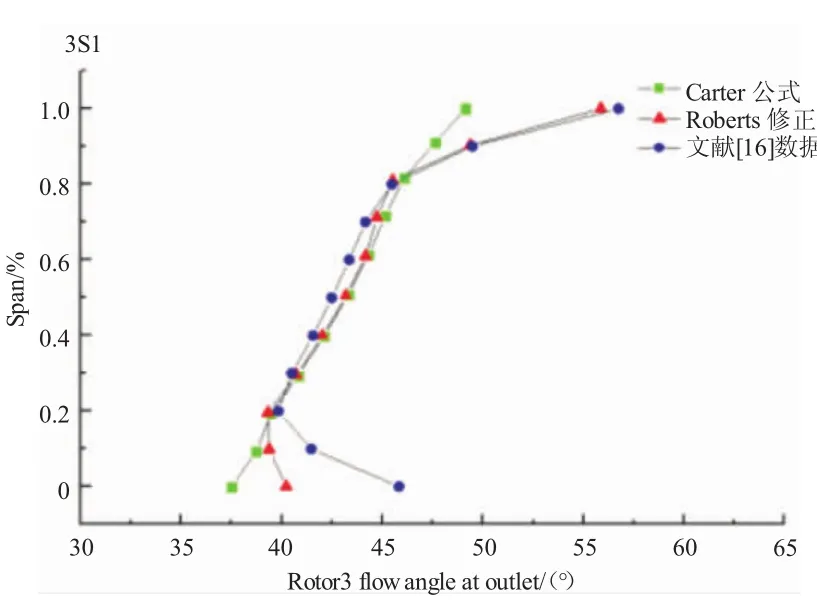
圖2 轉(zhuǎn)子3出口氣流角

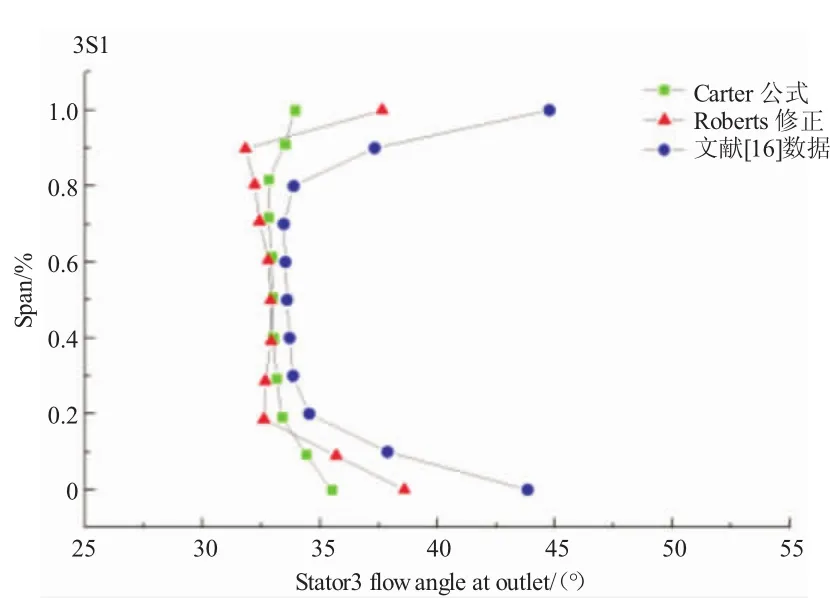
圖3 靜子3出口氣流角

第3級(jí)轉(zhuǎn)子和靜子的出口子午速度分別如圖4、5所示。從圖4中可見，前4種方案在20%～80%葉身部分的數(shù)據(jù)差距很小，其中方案（1）和（3）的數(shù)值與文獻(xiàn)數(shù)據(jù)更接近，數(shù)值上比方案（1）和（3）小0.5左右，但端壁區(qū)相差過(guò)多。方案（2）和（4）顯著改善了端壁區(qū)的情況，這正反映了改善后的Roberts模型使端部流動(dòng)計(jì)算得到明顯優(yōu)化。方案（4）的展向數(shù)值均比方案（2）的稍小，總體上優(yōu)于方案（2）的。圖5的情況與圖4類似，主流區(qū)4種方案相差不大，端壁區(qū)是方案（2）和（4）優(yōu)于方案（1）和（3），而總體上方案（4）又優(yōu)于方案（2）。

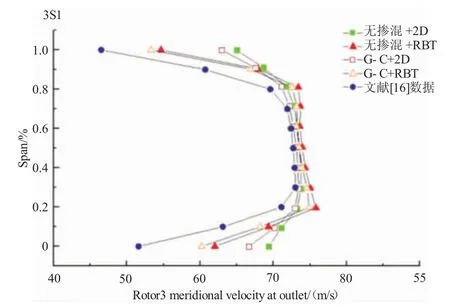
圖4 轉(zhuǎn)子3出口子午速度

圖5 第3級(jí)出口子午速度

3S1第3級(jí)出口總壓和總溫沿展向的分布如圖6、7所示。對(duì)于出口總壓，方案（1）在數(shù)值上已經(jīng)較文獻(xiàn)數(shù)據(jù)偏高，且在展向分布上近似成1條直線；方案（2）的展向分布形態(tài)較方案（1）有了明顯改善，但數(shù)值上比文獻(xiàn)數(shù)據(jù)小，且絕對(duì)誤差變大；方案（3）的展向分布較方案（1）在端壁區(qū)有所改善，但數(shù)值上反而更大。可以這樣理解：方案（1）假定流動(dòng)等熵和無(wú)黏，且滯止轉(zhuǎn)焓沿流線為定值。G-C模型改變了這一假定，焓值沿流線的梯度為正值，從而溫升變大。在損失系數(shù)不變的情況下，壓比變大。方案（4）結(jié)合了方案（2）和（3）的優(yōu)點(diǎn)，在數(shù)值和展向分布形態(tài)上都更加接近文獻(xiàn)數(shù)據(jù)。主流區(qū)二者幾乎重合，在端壁區(qū)方案（4）的變化幅度偏大，但總體上已經(jīng)達(dá)到了較高的計(jì)算精度。對(duì)于出口總溫，各方案結(jié)果與出口總壓的情況類似，方案（4）同樣取得最佳的結(jié)果，主流區(qū)與文獻(xiàn)數(shù)據(jù)幾乎重合，葉根和葉尖處均出現(xiàn)2 K左右的誤差。

需要指出的是，本文對(duì)Roberts模型在轉(zhuǎn)子葉根處的結(jié)果進(jìn)行改進(jìn)，但對(duì)于具體的取值尚需要進(jìn)行更深入的理論分析和總結(jié)，得到明確的計(jì)算公式，最終能應(yīng)用于工程實(shí)際。

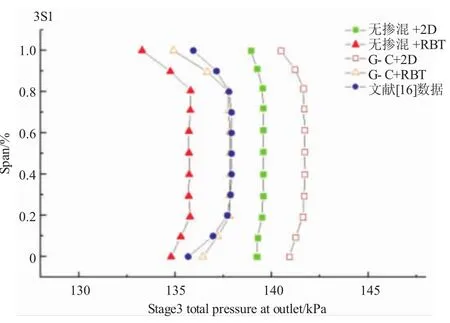
圖6 第3級(jí)出口總壓

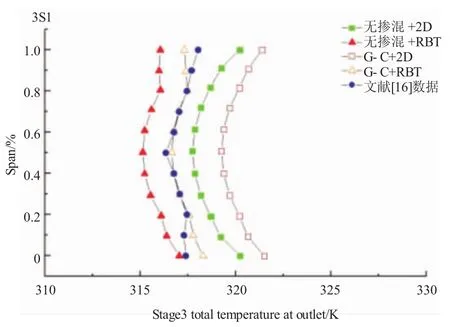
圖7 第3級(jí)出口總溫

3 結(jié)論

采用流線曲率法的數(shù)學(xué)模型，通過(guò)G-C模型模擬紊流擴(kuò)散的作用，通過(guò)落后角反映二次流的作用。在2維Carter公式基礎(chǔ)上引入改善的Roberts修正模型對(duì)落后角進(jìn)行預(yù)估，發(fā)展了1種考慮壓氣機(jī)內(nèi)展向摻混作用的計(jì)算方法。經(jīng)過(guò)數(shù)值計(jì)算，將計(jì)算值與文獻(xiàn)給出的數(shù)據(jù)進(jìn)行對(duì)比，得到如下結(jié)論：

（1）展向摻混對(duì)軸流壓氣機(jī)氣動(dòng)參數(shù)的展向分布有重要影響。單純的無(wú)摻混計(jì)算所得結(jié)果與實(shí)際的展向分布情況偏離較大，所以在壓氣機(jī)氣動(dòng)設(shè)計(jì)和優(yōu)化過(guò)程中應(yīng)當(dāng)考慮摻混這一重要因素。

（2）小尺度的紊流擴(kuò)散和大尺度的二次流都是展向摻混的重要因素。分析本文運(yùn)用流線曲率法得到的計(jì)算結(jié)果，可以看到單獨(dú)考慮Gallimore-Cumpsty模型或單獨(dú)采用Roberts對(duì)2維Carter公式的修正都不能得到很好的結(jié)果，只有同時(shí)考慮這2種因素才能獲得最優(yōu)方案，無(wú)論展向分布還是數(shù)值都與文獻(xiàn)數(shù)據(jù)最為貼近。

（3）本文改善了Roberts模型在轉(zhuǎn)子葉根處的計(jì)算方法，但只作了初步探究，后面仍需進(jìn)一步分析討論。

（4）本文采用的方法能夠較好地預(yù)測(cè)軸流壓氣機(jī)的氣動(dòng)特性，可以進(jìn)一步運(yùn)用到后續(xù)的分析和優(yōu)化工作中。

[1]Adkins G G，Smith L H Jr.Spanwise mixing in axial flow turbomachines[R].ASME 1981-GT-57.

[2]Gallimore SJ，Cumpsty N A.Spanwise mixing in multistage axial flow compressor：PartⅠ[R].ASME 1986-GT-20.

[3]Gallimore SJ，Cumpsty N A.Spanwise mixing in multistage axial flow compressor：PartⅡ[R].ASME 1986-GT-21.

[4]Wisler D C，Bauer R C，Okiishi T H.Secondary flow turbulent diffusion and mixing in axial flow compressor[R].ASME 1987-GT-16..

[5]Leylek J H，Wisler D C.Mixing in axial-flow compressor：conclusion drawn from 3D N-S analysis and experiments [R].ASME 1990-GT-352.

[6]李士明，陳懋章.多級(jí)軸流壓氣機(jī)的徑向摻混[J].航空學(xué)報(bào)，1991，12（11）：593-596 LI Shiming，CHEN Maozhang.Mixing for multi-stage axial-flow compressors[J].Acta Aeronautica et Astronautica Sinica，1991，12（11）：592-599.（in Chinese）

[7]Casey M C.Robinson.A new streamline curvature throughflow method for radial turbomachinery[J].Journal of Turbomachinery，2010，132（3）：031021.

[8]朱方元.計(jì)及氣流展向摻混影響多級(jí)軸流壓氣機(jī)通流數(shù)值計(jì)算[J].工程熱物理學(xué)報(bào)，1989，10（3）：265-266 ZHU fangyuan.Through flow numerical calculation of multi-stage axial flow compressor considering spanwise mixing[J].Journal of Engineering Thermodynamics，1989，10（3）：265-268.（in Chinese）

[9]Baldwin B S，Lomax H.Thin layer approximation and algebraic model for separated turbulent flows[R].AIAA-78-257.

[10]Visbal M，Knight D.Evaluation of the bladwin-lomax turbulence model for two dimensional shock wave boundary layer interaction[R].AIAA-70-741.

[11]朱方元，周新海，劉松齡，等.軸流跨音速壓氣機(jī)級(jí)的氣動(dòng)設(shè)計(jì)方法[J].西北工業(yè)大學(xué)學(xué)報(bào)，1979（1）：17-19.ZHU fangyuan，ZHOU xinhai，LIU songling，et al.Aerodynamic design methods of transonic axial flow compressor stages[J].Journal of Northwestern Polytechnical University，1979（1）：17-19.（in Chinese）

[12]Roberts W B，Serovy G K，Sandercock D M.Modeling the 3D Flow effects on deviation angle for axial compressor middle stages[R].ASME 1985-GT-189，1986.

[13]Britsch W R，Walter M O，Mark R L.Effects of diffusion factor，aspect ratio，and solidity on overall performance of 14 compressor middle stages[R].NASA-TP-1979-1523.

[14]姚吉先.軸流壓氣機(jī)氣動(dòng)設(shè)計(jì)方法研究[D].西安：西北工業(yè)大學(xué)，1992.YAO jixian.Research on aerodynamic design method of axial flow compressor[D].Xi’an：Northwestern Polytechnical University，1992.（in Chinese）

[15]Burdsall E A，Canal E，Lyons K A.Core compressor exit stage study,partⅠ.aerodynamic and mechanical design[R].NASA-CR-1979-159714.

[16]Behlke R F，Burdsall E A，Canal E，et al.Core compressor exit stage studyⅡ.final report[R].NASA-CR-1979-159812.