分類討論 巧妙解題

尹琳琳

在解決一個問題時，有時無法用同一種方法去解決，需要用一個標準將問題劃分成幾個能用不同方法去解決的小問題，再將這些小問題一一加以解決，從而使整個問題得到解決,這就是分類討論思想.

例1 （2016·西寧）⊙O的半徑為1，弦AB=，弦AC=，則∠BAC度數為 .

【分析】連接OA，分AB、AC在OA的同側、兩側兩種情況求∠BAC的度數.過O作OE⊥AB于E，OF⊥AC于F，根據垂徑定理求出AE、FA值，根據解直角三角形的知識求出∠OAB和∠OAC.

解：有兩種情況：

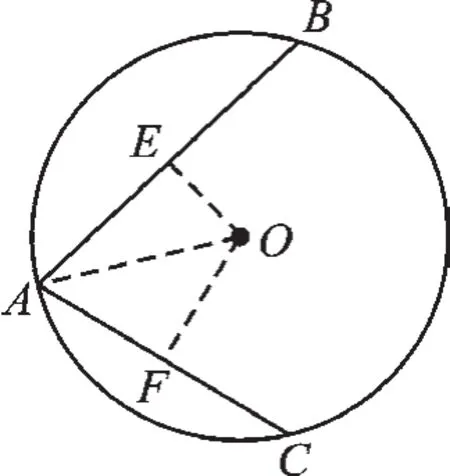
圖1

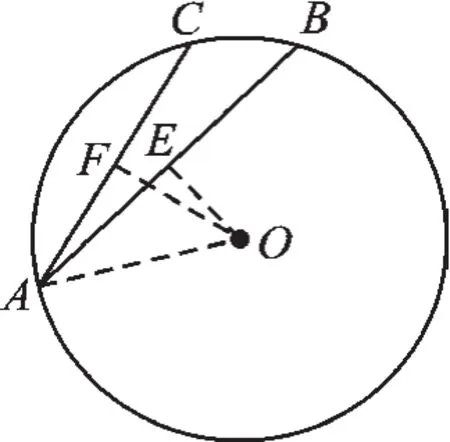
圖2

①如圖1所示：連接OA，過O作OE⊥AB于E，OF⊥AC于F，∴∠OEA=∠OFA=90°，

由垂徑定理得：AE=BE=，

同理∠OAF=45°，∴∠BAC=30°+45°=75°；

②如圖2所示：

∴∠BAC=45°-30°=15°；

故答案為：75°或15°.

【點評】本題考查了特殊角的三角函數值和垂徑定理的應用.解題的關鍵是根據題意作出圖形，求出符合條件的所有情況.

例2 （2017·河南）如圖3，在Rt△ABC中，∠A=90°，AB=AC，BC=2+1，點M，N分別是邊BC，AB上的動點，沿MN所在的直線折疊∠B，使點B的對應點B′始終落在邊AC上，若△MB′C為直角三角形，則BM的長為 .

圖3

【分析】如圖4，當∠B′MC=90°，B′與A重合，M是BC的中點，于是得到結論；如圖5，當∠MB′C=90°，推出△CMB′是等腰直角三角形，得到CM=2MB′，列方程即可得到結論.

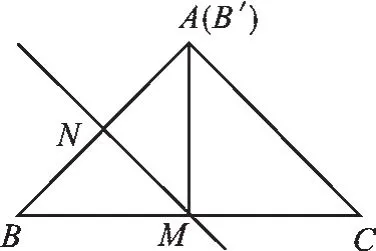
圖4

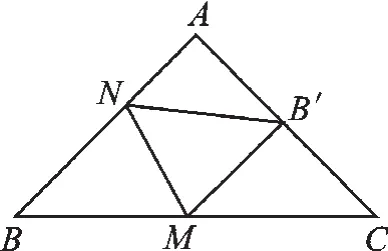
圖5

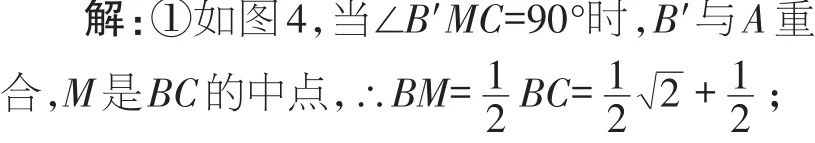
②如圖5，當∠MB′C=90°時，

∵∠A=90°，AB=AC，∴∠C=45°，

∴△CMB′是等腰直角三角形，

∴CM=2MB′，

∵沿MN所在的直線折疊∠B，使點B的對應點為B′，∴BM=B′M，∴CM=2BM，

∵BC=2+1，

∴CM+BM=2BM+BM=2+1，

∴BM=1.

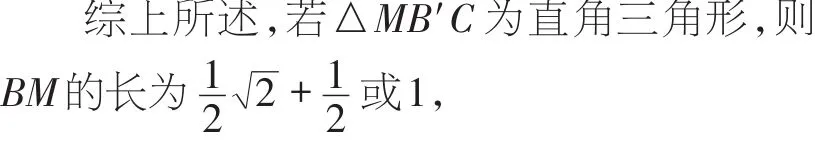
【點評】本題考查了翻折變換的折疊問題、等腰直角三角形的性質，正確作出圖形是關鍵.

例3 （2017·濰坊改編）如圖6，拋物線y=ax2+bx+c經過平行四邊形ABCD的頂點A（0，3）、B（-1，0）、D（2，3），拋物線與x軸的另一交點為E.經過點E的直線l將平行四邊形ABCD分割為面積相等的兩部分，與拋物線交于另一點F.點P是直線l上方拋物線上一動點，設點P的橫坐標為t.

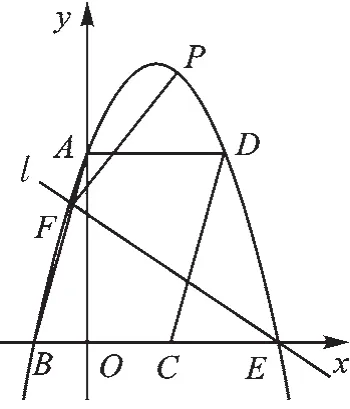
圖6

（1）求拋物線的解析式；

（2）是否存在點P使△PAE為直角三角形？若存在，求出t的值；若不存在，說明理由.

【分析】（1）由A、B、D三點的坐標，利用待定系數法可求得拋物線解析式；（2）由題意可知有∠PAE=90°或∠APE=90°兩種情況，當∠PAE=90°時，作PG⊥y軸，利用等腰直角三角形的性質可得到關于t的方程；當∠APE=90°時，作PK⊥x軸，AQ⊥PK，則可證得△PKE∽△AQP，利用相似三角形的性質可得到關于t的方程.

∴拋物線解析式為y=-x2+2x+3.

（2）由圖可知∠PEA≠90°，

∴只能有∠PAE=90°或∠APE=90°，

y=-x2+2x+3=-（x+1）（x-3），

∴點E的坐標為（3，0）.

點P的坐標為（t，-t2+2t+3）.

①當∠PAE=90°時，如圖7，作PG⊥y軸，

圖7

∵OA=OE，∴∠OAE=∠OEA=45°，

∴∠PAG=∠APG=45°，∴PG=AG，

∴t=-t2+2t+3-3，即-t2+t=0，解得t=1或t=0（舍去）；

②當∠APE=90°時，如圖8，

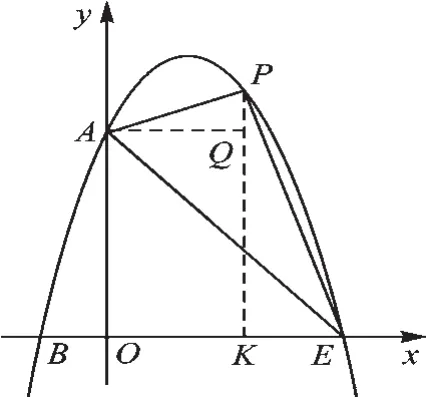
圖8

作PK⊥x軸，AQ⊥PK，則PK=-t2+2t+3，AQ=t，KE=3-t，PQ=-t2+2t+3-3=-t2+2t，

∵∠APQ+∠KPE=∠APQ+∠PAQ=90°，

∴∠PAQ=∠KPE，且∠PKE=∠PQA，

【點評】本題為二次函數綜合應用，涉及待定系數法、二次函數的性質、直角三角形的性質、相似三角形的判定和性質、方程思想和分類討論思想等知識.本題綜合性較強，計算量較大，難度較大.