細說數學中的方程思想
白廣明
從問題的數量關系入手,運用數學語言將問題中的條件轉化為數學模型(方程、不等式或方程與不等式的組合),將問題中的已知量和未知量之間的數量關系通過適當設元建立起方程(組),然后通過解方程(組)或不等式(組)來使問題獲解的思維方式是方程思想.
一、函數中的方程思想
方程與函數本身就有必然的聯系,通過建立相等關系,求出未知數的值,因此解決函數問題的關鍵就是找出相等關系,建立變量之間的等量關系.此類問題常見的形式和解題方法有:用待定系數法列出關于函數解析中待定系數的方程(組),通過解方程(組)求出待定系數的值;將函數圖像及坐標軸交點坐標與方程的根對應起來;利用一元二次方程根與系數關系解題.
例1 (2017·安順)如圖1,直線y=-x+3與x軸、y軸分別交于點B、點C,經過B、C兩點的拋物線y=x2+bx+c與x軸的另一個交點為A,頂點為P.
(1)求該拋物線的解析式;
(2)在該拋物線的對稱軸上是否存在點M,使以C,P,M為頂點的三角形為等腰三角形?若存在,請直接寫出符合條件的點M的坐標;若不存在,請說明理由.

圖1
【分析】(1)由直線解析式可求得B、C坐標,利用待定系數法可求得拋物線解析式;(2)由拋物線解析式可求得P點坐標以及對稱軸方程,再分MC=MP、MC=PC和MP=PC三種情況,便可得到關于M點坐標的方程,從而求得M點的坐標.
解:(1)∵直線y=-x+3與x軸、y軸分別交于點B、C,
∴B(3,0),C(0,3),
∵拋物線y=x2+bx+c過B、C兩點,

∴拋物線解析式為y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∴拋物線對稱軸為x=2,P(2,-1),設M(2,t),且C(0,3),
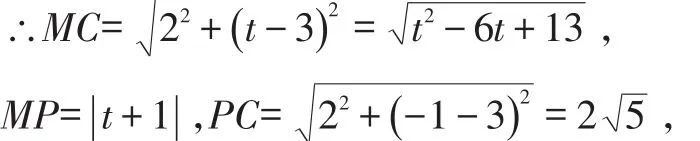
∵△CPM為等腰三角形,

③當PC=PM時,則有 | t+1|=2,解得t=-1+25或t=-1-25,此時M(2,-1+2)或M(2,-1-25).
綜上所述,存在滿足條件的點M,其坐標為:(2,)或(2,7)或(2,-1+25)或(2,-1-25).
【點評】本題是函數與方程相結合的綜合題,找出等量關系、構建方程是解決這類問題的關鍵,同時,又考查了分類討論思想.
二、解直角三角形中的方程思想
解直角三角形充分體現了數形結合思想,方程思想體現在:利用勾股定理建立方程,利用三角函數建立等量關系,利用圖形的性質建立等量關系.
例2 (2017·宿遷)如圖2所示,飛機在一定高度上沿水平直線飛行,先在點A處測得正前方小島C的俯角為30°,面向小島方向繼續飛行10km到達B處,發現小島在其正后方,此時測得小島的俯角為45°.如果小島高度忽略不計,求飛機飛行的高度(結果保留根號).

圖2
【分析】過點C作CH⊥AB,垂足為H,則CH的長度即為飛機飛行的高度.設CH=xkm,在Rt△ACH中,用x表示出AH的長,在Rt△BCH中,∠BHC=90°,可得BH=CH=x,根據AH+HB=10列出方程,解方程求得x的值,即飛機飛行的高度.

圖3
解:如圖3,過點C作CH⊥AB,垂足為H,設CH=xkm,在Rt△ACH中,∠AHC=90°,∠CAH=30°,所以AH=3x;在Rt△BCH中,∠BHC=90°,∠CBH=45°,所以BH=CH=x.因為AH+HB=10,所以 3x+x=10,解得x==5-5.
答:飛機飛行高度為(53-5)km.
【點評】構造直角三角形是解直角三角形問題的關鍵,之后再適當設未知數,建立相等關系列出方程,求出未知數的值即可解答.
三、整式中的方程思想
整式中很多內容與方程有必然的聯系,同類項的定義以及整式的化簡中就隱含著相等關系,解決這類題的方法:同類項的定義,代數中的恒等變形,利用對比法.
例3 已知A=7x2-mx+n,B=-4y2+2x-1,若A+B中不含有一次項和常數項,求m2-2mn+n2的值.

∴m2-2mn+n2=(m-n)2=1.
例4 單項式3x2y5m+4n與-2xm+2ny4是同類項,求nm的值.

【點評】根據同類項的定義,所含字母相同,相同字母的指數相同,可列出關于m,n的方程組,再求解.
四、幾何問題中的方程思想
數與形的結合思想是求解數學問題的重要思想方法,它會使抽象的問題具體化,復雜的問題簡單化.與幾何圖形有關的計算題,若可用方程思想去建立等量關系來解決,會使問題簡單化.
1.三角形和四邊形與方程思想.
例5 (2016·揚州)如圖4,AC為矩形ABCD的對角線,將邊AB沿AE折疊,使點B落在AC上的點M處,將邊CD沿CF折疊,使點D落在AC上的點N處.
【分析】A+B中不含有一次項和常數項,即A+B中一次項系數和常數項都為0,構建方程組求解.
解:A+B=7x2-mx+n+(-4y2+2x-1)
=7x2-4y2+(-m+2)x+n-1,

圖4
(1)求證:四邊形AECF是平行四邊形;
(2)若 AB=6,AC=10,求四邊形 AECF 的面積.
【分析】(1)先利用“兩直線平行,內錯角相等”證明∠BAC=∠DCA,根據折疊的性質得出角相等,即∠BAE=∠EAC,∠DCF=∠NCF,進而得出∠EAC=∠FCA,再根據“內錯角相等,兩直線平行”,得出AE∥CF,從而證明四邊形AECF是平行四邊形;(2)可以先在Rt△ABC和Rt△CME中利用勾股定理構造方程求得CE的長度,再根據平行四邊形的面積公式求得四邊形AECF的面積.
證明:(1)∵四邊形ABCD是矩形,
∴AB∥CD,∴∠BAC=∠DCA,
由折疊可得∠BAE=∠EAC=∠BAC,
∠DCF=∠NCF=∠DCA,
所以∠EAC=∠FCA,AE//CF,
∴四邊形AECF是平行四邊形.
(2)因為AB=6,AC=10,△ABC為直角三角形,由勾股定理,得BC=8.設EM=x,那么BE=EM=x,所以CE=BC-BE=8-x,CM=AC-AM=ACAB=10-6=4.
所以x2+42=(8-x)2,解得x=3.
所以S四邊形AECF=2S△ACE

【點評】本題通過設未知數列方程求解,體現了變量間的關系,運用了方程思想.
2.圓與方程思想.
例6 如圖5,從⊙O外一點A作⊙O的切線AB、AC,切點分別為B、C,且⊙O直徑BD=6,連接CD、AO.
(1)求證:CD∥AO;
(2)設CD=x,AO=y,求y與x之間的函數關系式,并寫出自變量x的取值范圍;
(3)若AO+CD=11,求AB的長.

圖5
【分析】(1)連接BC交OA于E點,根據切線長定理和等腰三角形中三線合一定理,可得∠OEB=90°,根據直徑對的圓周角為直角可得∠BCD=90°,再根據“同位角相等,兩直線平行”即可證明CD∥AO;(2)如圖6,根據“兩直線平行,同位角相等”,可得∠3=∠4,再證得△BCD∽△ABO,根據相似三角形對應邊成比例的性質可得到y與x的關系式,再由題意可得x的取值范圍;(3)由(2)中關系式和(3)中的條件可得到關于x和y的方程組,解方程組可得CD,AO的長,再在Rt△AOB中根據勾股定理求得AB的長.
解:(1)連接BC交OA于E點,

圖6
∵AB、AC是⊙O的切線,
∴AB=AC,∠1=∠2,
∴AE是△ABC的中線,
∵O是BD的中點,∴CD∥AO.
(2)∵CD∥AO,∴∠3=∠4,
∵AB是⊙O的切線,DB是直徑,∴∠DCB=∠ABO=90°,

【點評】這是一道典型的應用方程求解的幾何問題,相等關系是利用了相似三角形的性質和一元二次方程根與系數的關系,體現了數形結合的思想.

