“圓周角(第1課時)”教學設計及反思
■郭 英
在小學五年級,學生已經認識了圓,通過本章前兩節內容的學習,學生對圓的基本概念和性質又有了更深刻的了解,學會了畫圓的方法,知道了圓的半徑、直徑之間的關系,圓心角、弧、弦的概念,圓的對稱性,這些都為本節課的學習奠定了基礎。
通過對圓的性質、直線與圓的位置關系、圓與圓的位置關系的探索,學生能在直觀的基礎上學習說理,實現合情推理與演繹推理的融合。本章在發展學生有條理地思考和表達、發展學生思維品質等方面,起著承上啟下的作用。
一、設計思路
本節課的設計依據《義務教育數學課程標準(2011年版)》要求,按照“問題情境→建立模型→自主探究→解釋應用”展開教學,即以古代航標燈的圖片為問題情境→點和圓的位置關系→頂點在圓外、圓上、圓內的角→圓周角的概念→圓心與圓周角的位置→探索圓周角的性質→解決問題(古代航標燈的作用),以此深化學生對圓周角的概念及其性質的理解。
在教材處理方面,首先,筆者注重創設生活情境,讓學生感知數學來源于生活,應用于生活,對教材中的“操作與思考”進行了處理,從學生已經掌握的點和圓的位置關系入手,讓學生經歷圓周角的形成過程,過渡比較自然。其次,筆者注重讓學生在“做”中學。通過畫圓周角,學生能進一步理解圓周角的概念,這為下一步探索圓心和圓周角的位置埋下伏筆;通過幾何畫板度量一條弧所對的圓周角和圓心角,學生能形成一個感性認識:同弧所對的圓周角等于該弧所對的圓心角的一半,這為證明圓周角的性質做鋪墊。教學過程中筆者注重讓學生自己畫圖,自己度量,自主探究,使學生真正成為學習的主人。再次,筆者注重讓學生“說”數學,提供盡可能多的機會讓學生展示交流,提高學生的語言表達能力。另外,本節課運用了類比、分類、轉化等數學思想方法突破難點,一是類比圓心角得出圓周角的概念,二是運用分類、轉化思想探索圓周角的性質。解釋應用環節,重新整合了教材例題和練習,既注重了性質的直接應用,又回應開頭情境引入中提出的問題,讓學生體會數學來源于生活,又服務于生活。
二、教學目標
日常生活中處處有數學,根據學生的認知水平,讓實際問題數學化,能進一步加深學生對圓周角的認識。由于學生已積累了一定的操作活動經驗,所以在教學中積極鼓勵學生操作、探索、交流,不僅能讓學生了解圓周角的概念,而且能讓學生不斷積累數學活動的經驗,發展學生從不同的角度觀察問題的能力。基于上述因素,根據《義務教育數學課程標準(2011年版)》確定本節課的教學目標如下:
理解圓周角的概念及其性質,并能運用相關性質解決問題;經歷探索圓周角與圓心角及其所對弧的關系的過程,發展推理能力;在觀察、操作、猜想、驗證等活動中,體會分類、轉化等數學思想,培養合作意識和探究精神。
三、教學重、難點
教學重點:圓周角性質的探索與證明;
教學難點:探索圓周角的性質。
四、教學過程
1.情境創設。
師:這是我國古代航海的燈塔(教師指著投影中的燈塔)!它是當時海上航行必不可少的航標。過往的船只,通過測量航船與兩座燈塔形成的角的大小(多媒體生成夾角),便可以判斷船是否在安全航道行駛。你知道其中的奧秘嗎?
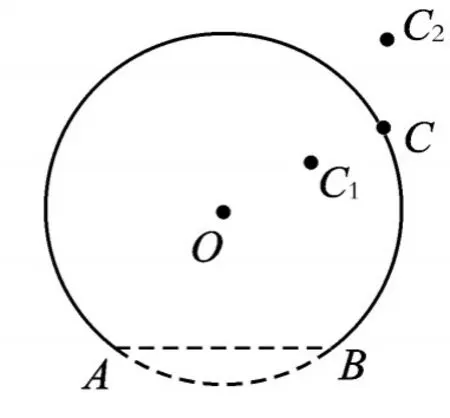
圖2

圖1
設計意圖:通過實際問題創設情境,學生體會數學來源于生活,激起學生探究的欲望。
2.探索活動。
活動一 揭示圓周角的概念。
(1)說一說:點與圓有哪幾種位置關系?
(2)畫一畫:在操作紙上任意畫出這幾種位置關系。圓上的點記作點C,圓內和圓外的點分別記作點C1和點C2,并分別畫出它們與點A、點B形成的角
(3)量一量:分別度量的大小。(結果保留整數)
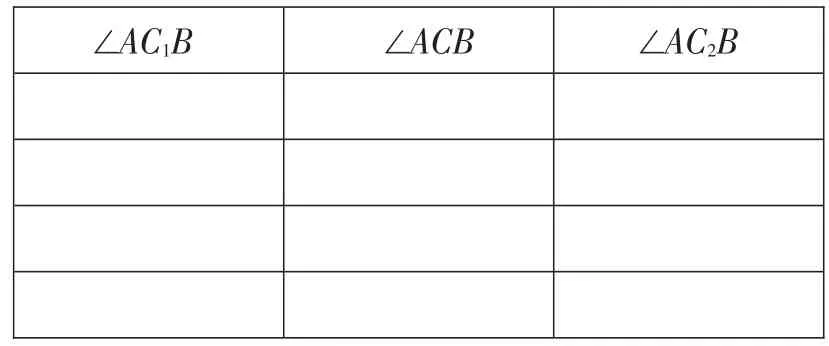
∠AC1B ∠ACB ∠AC2B
(4)議一議:觀察上述表格中的幾組數據,你有什么發現?
設計意圖:將實際問題轉化為數學問題——點與圓的位置關系,讓學生經歷動手畫圖、測量、思考、討論等活動,并初步感知點C在圓外、圓上、圓內時與圓上的兩點A、B所形成的角之間的大小關系。引導學生觀察圓周角的特征,類比圓心角,從而揭示圓周角的概念。
活動二 探索圓周角的性質。
(1)操作思考。
請同學們在操作用紙上任?意畫出所對的一個圓周角。你還能畫出?所對的其他的圓周角嗎?再在圖中畫出?所對的圓心角。所對的圓周角有多少個?所對的圓心角有多少個?觀察圖形,圓心與所畫的圓周角有哪些位置關系?
(?2)猜想驗證。 ?
所對的圓周角與所對的圓心角有什么數量關系?并說明理由。
a.利用幾何畫板度量圓周角和圓心角的大小,得出結論。
b.借助下列圖形,證明上述結論。學生將這一個數學問題現實化,從而解決情境導入中的問題。)

圖6

圖7
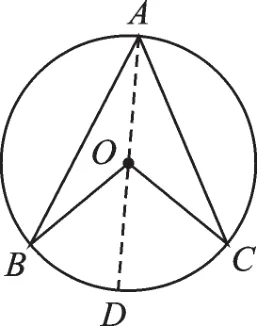
圖4

圖5
設計意圖:學生通過畫圖、觀察、思考等活動,歸納得出圓心在圓周角的一邊上、內部、外部3種位置關系,并猜想同弧所對的圓周角與圓心角的數量關系。讓學生先通過幾何畫板度量發現結論,形成一個感性認識,為下一步證明圓周角的性質做鋪墊;再引導學生自主探索、合作交流,從特殊入手,發展到一般。而解決一般情況又要用到特殊的結論,學生對數學思想方法便有了進一步認識。
3.展示交流。
(1)如圖6,點A、B、C、D在⊙O上,點A與點D 在點 B、C所在直線的同側,∠BAC=35°。∠BDC=______ _°,理由是_______;∠BOC=______°,理由是_______。
(2)如圖7,點A、B、C在⊙O上,點D在圓外,CD、BD分別交⊙O于點E、F。比較∠BAC與∠BDC的大小,并說明理由。(學生獨立思考,小組交流后向全班展示。問題解決后,教師引導
設計意圖:問題(1)是圓周角的性質的直接應用,主要是讓學生熟悉圓周角的性質;問題(2)讓學生學會構造圓周角探索結論,學會嚴格地說理,并為開頭情境引入做好回應。
4.小結反思。
通過這節課的學習,你有哪些收獲?
設計意圖:引導學生學會歸納、總結、反思,培養學生良好的學習習慣。
5.作業設計。
必做題:教材第122頁習題5.3第1、2題;選做題:教材第122頁習題5.3第3題。
設計意圖:作業設計分層要求,滿足不同層次學生發展的需要。
五、教學反思
《義務教育數學課程標準(2011年版)》指出,有效的數學學習活動不能單純地依賴模仿和記憶,動手實踐、自主探索與合作交流是學生學習的重要方式。在這節課的教學過程中,筆者著力突出學生學習方式的轉變,力求讓學生參與,采取小組合作探究、展示交流的形式,激勵學生主動探索,主動發現,主動思考,積極發表自己的見解。教師起組織引導的作用,參與學生的小組活動,適時發問、追問,提出有價值的問題,激發學生思考,引導學生前行。前期學生畫圖較慢,花費較多時間,導致后期時間較短,探索圓周角的性質這個環節完成得比較倉促。

