按類統(tǒng)計方法在滾動軸承可視化 可靠性動態(tài)評估中的應用

孟文俊,張四聰,淡紫嫣,劉彈,徐光華,2

(1.西安交通大學機械工程學院,710049,西安; 2.西安交通大學機械制造系統(tǒng)工程國家重點實驗室,710054,西安)

機械設(shè)備在運行過程中一旦某個零部件發(fā)生故障,往往會影響整個機械設(shè)備的性能,有可能造成巨大的經(jīng)濟損失[1-3],而滾動軸承是旋轉(zhuǎn)機械中關(guān)鍵的零部件,其可靠性與壽命直接影響設(shè)備的使用壽命和運行可靠性[4]。因此,開展運行性能可靠性的研究,確保設(shè)備安全運行和預防事故發(fā)生是十分必要的。

滾動軸承運行性能可靠性評估的核心問題是從大量的性能指標序列中提取穩(wěn)定的退化軌跡,建立滾動軸承性能指標的概率模型,從而對軸承的退化程度進行評判。傳統(tǒng)研究主要采用基于失效規(guī)律和統(tǒng)計學的運行性能可靠性評估。Lu等人假設(shè)機械設(shè)備的性能指標服從正態(tài)分布,通過計算分布函數(shù)中超過失效閾值的部分,實現(xiàn)單個設(shè)備可靠性的評估[5]。西安交通大學丁峰等人把表征設(shè)備退化狀態(tài)的特征值和傳統(tǒng)可靠性的統(tǒng)計模型與比例故障率模型進行結(jié)合,實現(xiàn)了滾動軸承可靠性的評估[6]。Nelson假設(shè)設(shè)備性能指標的對數(shù)服從一種分布均值隨時間變化、而方差隨時間不變的正態(tài)分布,通過該分布模型進行滾動軸承可靠性的評估[7]。

利用統(tǒng)計學進行可靠性評估的方法可以得到滾動軸承性能退化一般規(guī)律性的認識,但是傳統(tǒng)可靠性評估方法中的分布模型是一個需要先驗知識的靜態(tài)模型,需要大量的試驗數(shù)據(jù)和先驗知識對統(tǒng)計模型的參數(shù)進行修正,不會隨運行時間的變化自適應調(diào)整。這種參數(shù)化的統(tǒng)計模型需要明確滾動軸承退化規(guī)律的分布形式,對于在運行中的滾動軸承而言是難以實現(xiàn)的。

滾動軸承在壽命周期中,空間狀態(tài)并不連續(xù),當軸承逐漸退化,穩(wěn)定性逐漸減弱,可靠性逐漸下降,其空間狀態(tài)發(fā)生躍遷,概率模型的類別會逐漸增多。在國內(nèi)外研究中,均方根和峭度通常被用作滾動軸承壽命評估指標[8-11],所以本文以滾動軸承的均方根和峭度為分析對象,基于核密度法建立了動態(tài)按類概率模型,轉(zhuǎn)化為能夠直觀顯示滾動軸承退化狀態(tài)的按類概率圖像模型,并在按類概率圖像模型中計算非正常類的圖像分布區(qū)域面積占總圖像分布區(qū)域面積的比值,得到可靠性指標。通過分析樣本的不斷積累擴充進行模型更新,建立起動態(tài)可調(diào)的可視化按類概率圖像模型。概率圖像模型的類別數(shù)目用于判斷軸承的退化過程,得到的可靠性指標能夠反映軸承的退化程度。

1 滾動軸承動態(tài)按類概率圖像模型

將實時獲取的預處理后的性能指標數(shù)據(jù)作為研究對象,建立動態(tài)可調(diào)的按類統(tǒng)計概率模型,實現(xiàn)滾動軸承退化狀態(tài)的準確描述。為了使用多維性能指標序列建立包含更多信息的按類概率模型來反映滾動軸承的運行狀態(tài),本文提出了一種基于按類統(tǒng)計的滾動軸承可視化可靠性動態(tài)評估方法,具體流程如圖1所示。

圖1 基于按類統(tǒng)計的滾動軸承可視化可靠性動態(tài)評估流程

(1)通過性能指標序列獲取正常運行時刻的統(tǒng)計樣本,建立基于核密度法的初始按類概率模型,該類樣本為正常類。

(2)將初始按類概率模型進行可視化處理,得到初始按類概率圖像模型,且確定分類邊界線。

(3)提取按類概率圖像模型中的統(tǒng)計指標故障率,并計算可靠性指標。

(4)當有新性能數(shù)據(jù)時,根據(jù)分類邊界線進行類別判斷,建立新類別的概率圖像模型,并確定每類的分類邊界線,提取可靠性指標。

(5)隨著分析樣本的不斷累積,得到不同類的樣本,使按類概率圖像模型和可靠性指標不斷更新,實現(xiàn)滾動軸承可靠性的動態(tài)評估。

1.1 基于核密度法的動態(tài)按類概率圖像模型

核密度法是一種根據(jù)數(shù)據(jù)本身研究其分布特征的非參數(shù)估計法[12]。由于滾動軸承性能指標的原始概率密度分布是未知的,因此可以使用核密度法估計概率密度分布,消除隨機因素對概率密度分布的影響。

假設(shè)X={x1,x2,…,xm}為觀測數(shù)據(jù)序列,用核函數(shù)運算得到每個樣本點處的概率密度函數(shù)

(1)

式中:p為樣本維數(shù);σ為平滑因子;

對m個樣本點的概率密度分布曲線進行疊加,可以逼近設(shè)備原始狀態(tài)的概率密度分布

(2)

通過式(1)和式(2)可知,平滑因子就是該概率密度函數(shù)的標準差,對概率密度分布有重要影響。如果平滑因子σ選擇過大,使概率密度分布曲線變得平滑,不能很好地表達細節(jié)信息;如果σ過小,噪聲信息會對概率密度分布產(chǎn)生影響,無法有效識別有用信息中的噪聲干擾。

Cain通過大量實驗研究和對比發(fā)現(xiàn),平滑因子與樣本間平均最小距離有關(guān)[13]。樣本點間的平均最小距離為

i,j=1,2,…,m;i≠j

(3)

在計算樣本點之間距離時,當距離小于給定閾值(本文中取為0.001)時,認為兩個樣本點為同一個點。平滑因子可表示為

σ=gd

(4)

式中:g=1.1～1.4。

為了更準確地描述滾動軸承的退化狀態(tài),對樣本進行類別劃分,建立動態(tài)按類概率圖像模型,建立的流程如圖2所示。

(5)

將不同類的概率模型進行疊加,得到這一觀測時刻的按類概率模型

(6)

為了便于按類概率模型動態(tài)調(diào)整與圖形化顯示,式(5)在使用中并沒有除以加和前面的系數(shù)m。

在第k+1次觀測時,對新數(shù)據(jù)進行類別判斷,更新按類概率圖像模型。

圖2 動態(tài)按類概率圖像模型的建立流程

1.2 基于拉依達準則確定分類邊界線

本文通過拉依達準則確定不同類別之間的分類邊界線[14]。新樣本點落在(μ-3σ,μ+3σ)之外的概率僅為0.27%,在概率統(tǒng)計中認為是小概率事件,因此圖像模型中3σ處的概率值即為分類邊界線。

利用同類數(shù)據(jù)計算的平滑因子帶入該類單一樣本點的概率密度函數(shù)計算中,得到圖3所示的概率模型是一個以樣本點為中心的對稱圖形。在單一樣本點的概率密度分布曲線中,與中心距離相同的點只保留一個值,得到圖4所示的截面數(shù)據(jù)曲線。

圖3 單一樣本點的概率密度分布曲線

圖4 截面數(shù)據(jù)曲線

通過同類數(shù)據(jù)得到一個平滑因子σ,就可以確定一個類的概率圖像模型,通過對比新樣本點的概率與3σ處的概率,可以判斷新樣本點是否屬于這一類。求取新性能數(shù)據(jù)在圖像模型中的概率采用雙三次插值法[15]。判斷指標如下

p=pnew-pbie

(7)

式中:p為判斷指標;pnew為新樣本點處概率值;pbie為分類邊界處的概率值。

當p≥0,說明該樣本點在(μ-3σ,μ+3σ)范圍內(nèi),屬于本類;當p<0,新樣本點的概率小于邊界處的概率,即新樣本點超出了(μ-3σ,μ+3σ)的范圍。新性能數(shù)據(jù)為非本類數(shù)據(jù),此時產(chǎn)生了新的概率密度分布類型,說明此時滾動軸承的穩(wěn)定性有所下降。當每類的統(tǒng)計樣本更新時,平滑因子、分類邊界線也在不斷更新。

2 滾動軸承可靠性的動態(tài)評估

在獲取滾動軸承一定量正常統(tǒng)計樣本的基礎(chǔ)上,得到可靠性指標,實現(xiàn)滾動軸承可靠性的動態(tài)評估,具體流程如圖5所示。

圖5 滾動軸承可靠性動態(tài)評估流程

(1)本研究中的可視化按類概率模型是三維模型,所以以二維性能指標序列為基礎(chǔ),獲取滾動軸承的振動數(shù)據(jù),提取其均方根和峭度性能指標。

(2)由于不同維數(shù)據(jù)的離散程度會對概率模型產(chǎn)生影響,為了減小不同維數(shù)據(jù)離散程度的不一致性,對均方根和峭度指標進行如下的預處理

(8)

(3)獲取正常狀態(tài)下一定量的二維性能指標數(shù)據(jù)作為統(tǒng)計樣本,稱為正常類

(9)

(4)根據(jù)式(3)和式(4)計算正常類平滑因子,利用核密度法計算該類每個樣本點的概率密度分布曲線,并對m個樣本點的概率密度分布曲線進行疊加,得到初始按類概率模型

(10)

(5)將初始按類概率模型進行可視化,得到按類概率圖像模型,并確定分類邊界線。

(6)在按類概率圖像模型中,通過大于該類3σ概率的像素點數(shù)來估計每類圖像的分布區(qū)域面積。根據(jù)按類概率圖像模型中非正常類的圖像分布區(qū)域面積占總圖像分布區(qū)域面積的比值得到故障率,根據(jù)故障率計算出可靠性指標如下

(11)

式中:h(t)為故障率函數(shù)。

(7)當有新數(shù)據(jù)時,根據(jù)判斷指標p更新可靠性評估指標。p≥0時認為新數(shù)據(jù)為正常類數(shù)據(jù),p<0時將新數(shù)據(jù)作為另外一類。當這類中的樣本累加到一定量(本文設(shè)為5個)時,根據(jù)計算的平滑因子建立該類的概率模型,并確定分類邊界線。重復步驟(6)得到新的可靠性指標。一般來說,隨著軸承運行時間的增加,軸承可靠性降低,概率圖像模型的類別會逐漸增加。

(8)當又有新數(shù)據(jù)時,根據(jù)每類的分類邊界線進行類別判斷,屬于某一類就加入,不屬于其中一類就另成一類。通過數(shù)據(jù)的不斷積累,重復步驟(7),得到不同的按類概率圖像模型,從而得到不同時刻的可靠性指標。

3 實驗驗證

3.1 數(shù)據(jù)來源及說明

本文使用美國智能維護系統(tǒng)中心提供的滾動軸承壽命實驗數(shù)據(jù)進行分析。滾動軸承參數(shù)見表1。

表1 實驗軸承參數(shù)表

給定負載為27 kN,轉(zhuǎn)速為2 000 r/min。在每個軸承的軸承座上安裝PCB 353B33型加速度傳感器,通過6062E型數(shù)據(jù)采集卡每隔10 min對圖6中滾動軸承1進行信號采集,采樣頻率為20 kHz,采樣點數(shù)為20 480。軸承壽命為164 h,在壽命末期發(fā)生外圈故障。

圖6 滾動軸承壽命實驗裝置

3.2 滾動軸承的動態(tài)按類概率圖像模型

(1)性能指標的選取。將預處理后原始振動信號的均方根和峭度作為性能指標,得到滾動軸承運行115 h的特征指標變化,如圖7所示。

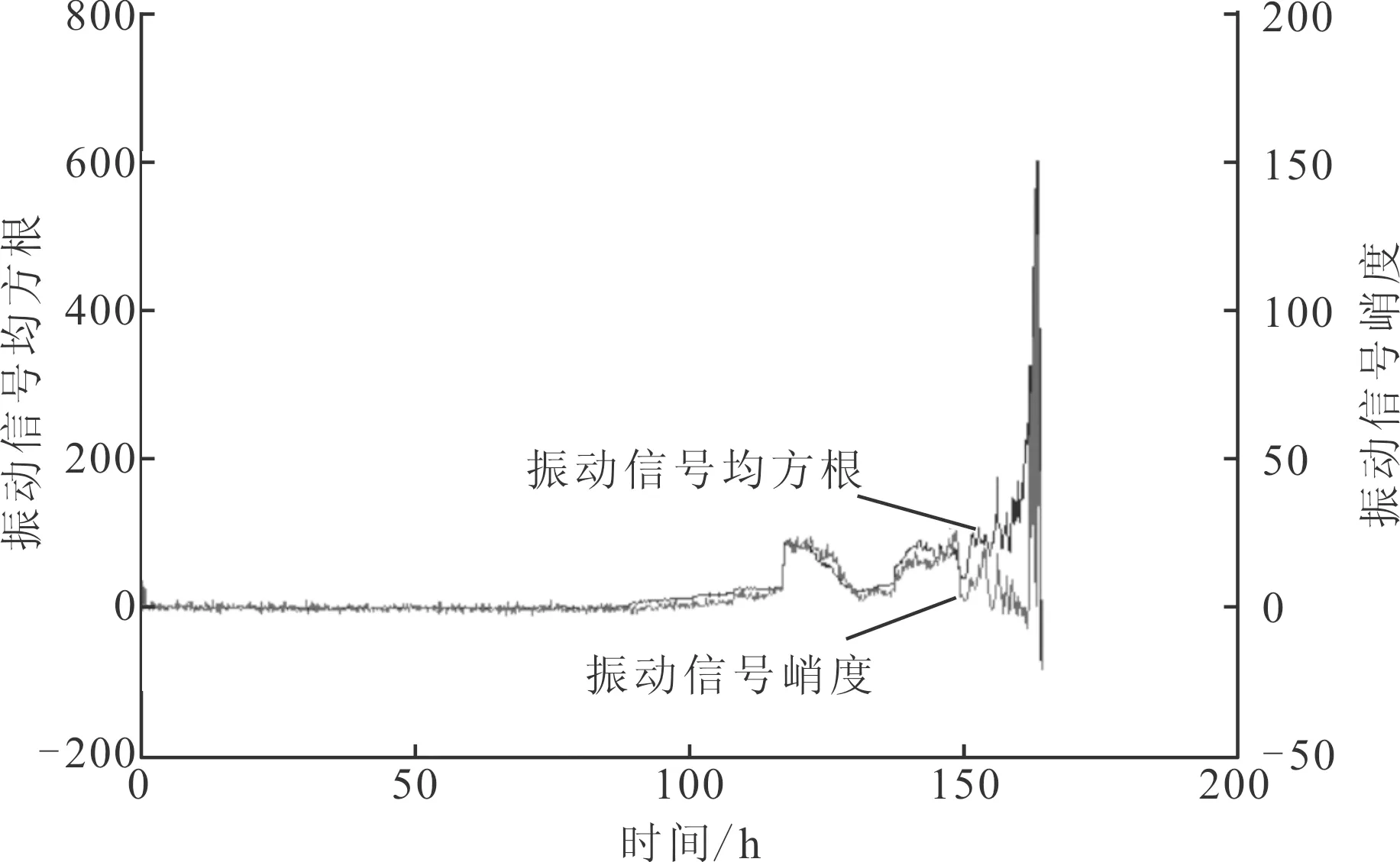
圖7 預處理后特征值變化趨勢

(a)33 h

(b)91 h

(c)115 h

(d)142 h圖8 按類概率圖像模型更新過程

(2)動態(tài)按類概率圖像模型。鑒于現(xiàn)有方法無法實時可視化顯示的問題,本文提出了按類可視化概率圖像模型,可實時更新設(shè)備運行時的可視化狀態(tài)。選擇二維性能指標序列的前100個樣本點建立初始按類概率模型,其更新過程見圖8。在剛開始運行階段,滾動軸承處于正常狀態(tài),性能指標數(shù)據(jù)變化較小,這些樣本點屬于正常類,按類圖像模型中只有這一類,如圖8a所示。隨著運行時間的增加,滾動軸承性能發(fā)生退化,性能指標數(shù)據(jù)變化率增大,按類圖像模型中的類型越來越多,如圖8b中有2類、圖8c中有3類、圖8d中有4類。因此,該圖像模型既融合了均方根指標和峭度指標,又能準確直觀地顯示滾動軸承的退化過程,進而準確地評估可靠性的下降程度。

3.3 滾動軸承實時可靠性評估

按類概率圖像模型中,根據(jù)非正常類的圖像面積占總圖像面積的比值得到故障率。以圖8d為例,每一類的區(qū)域面積即為白色分類邊界線包含的部分,其中正常類面積為S1,所以該圖中故障率為(S2+S3+S4)/(S1+S2+S3+S4),再通過式(11)可得到可靠性指標。

圖9為根據(jù)不同的按類概率圖像模型得到的滾動軸承實時可靠性指標曲線,可以看到:

(1)滾動軸承運行早期狀態(tài)平穩(wěn),特征指標分布的區(qū)域相對穩(wěn)定,可靠性指標為1;

(2)當運行時間達到89 h,可靠性指標開始下降,且隨著運行時間的增加,軸承不斷劣化,可靠性指標越來越小;

(3)當運行時間大約在115 h左右,可靠性指標幾乎為0,表明在115 h后滾動軸承處于故障后期階段。

圖9 滾動軸承實時可靠性指標曲線

為了驗證本文模型是否能夠及時跟蹤滾動軸承的退化過程,以及可靠性指標是否能夠?qū)崟r反映滾動軸承的退化程度,對89 h和115 h的振動數(shù)據(jù)進行包絡(luò)譜分析,并采用最小熵解卷積(MED)對原始數(shù)據(jù)進行降噪處理[16],結(jié)果如圖10、圖11所示。

從圖10、圖11中可以看出,故障特征頻率為230.5 Hz,非常接近實驗軸承的外圈故障特征頻率236.4 Hz。故障特征頻率的幅值隨著滾動軸承的退化逐漸增大,與實際結(jié)果吻合,表明本文模型能夠及時跟蹤滾動軸承的退化過程,得出的可靠性指標能夠?qū)崟r反映滾動軸承的退化程度。

圖10 89 h振動信號的包絡(luò)分析結(jié)果

圖11 115 h振動信號的包絡(luò)分析結(jié)果

4 結(jié) 論

針對目前滾動軸承性能指標的概率模型大多為單性能指標的靜態(tài)概率模型,且與實際概率模型誤差較大的問題,本文基于核密度法建立了動態(tài)按類概率圖像模型,并將該概率模型中各點的概率轉(zhuǎn)化為彩色值,得到一個能夠直觀顯示滾動軸承退化狀態(tài)的按類概率圖像模型。通過拉依達準則確定分類邊界線,并在按類概率圖像模型中計算非正常類的圖像面積占總圖像面積的比值,得到可靠性指標。通過分析樣本的不斷積累擴充進行模型的更新,實現(xiàn)了不同時刻滾動軸承可靠性的評估。實驗結(jié)果表明,基于按類統(tǒng)計的滾動軸承可視化可靠性動態(tài)評估技術(shù),可以實時準確評估滾動軸承的運行性能可靠性。

參考文獻:

[1] 屈梁生,何正嘉. 機械故障診斷學 [M]. 上海: 上海科學技術(shù)出版社,1986: 4-11.

[2] 黃文虎,夏松波,劉瑞巖,等. 設(shè)備故障診斷原理、技術(shù)及應用 [M]. 北京: 科學出版社,1996: 9-15.

[3] 徐敏,黃邵毅. 設(shè)備故障診斷手冊-機械設(shè)備狀態(tài)檢測和故障診斷 [M]. 西安: 西安交通大學出版社,1998: 1-5.

[4] 李海波. 智能化軸承故障診斷儀的工程設(shè)計與研制 [D]. 沈陽: 沈陽理工大學,2009: 1-3.

[5] LU H,KOLARIK W J,LU S S. Real-time performance reliability prediction [J]. IEEE Transactions on Reliability,2001,50(4): 353-357.

[6] 丁鋒,何正嘉,訾艷陽. 基于設(shè)備狀態(tài)振動特征的比例故障率模型可靠性評估 [J]. 機械工程學報,2009,45(12): 89-95.

DING Feng,HE Zhengjia,ZI Yanyang. Reliability assessment based on equipment condition vibration feature using proportional hazards model [J]. Journal of Mechanical Engineering,2009,45(12): 89-95.

[7] NELSON W. Analysis of performance degradation data from accelerated tests [J]. IEEE Transactions on Reliability,2006,91: 200-208.

[8] 馬家駒,梁文梅. 滾動軸承振動統(tǒng)計特性分析 [J]. 軸承,1994(1): 33-37.

MA Jiaju,LIANG Wenmei. Analysis of vibration statistical characteristics of rolling bearings [J]. Bearing,1994(1): 33-37.

[9] KALLAPPA P,BYINGTON C S,KALGREN P W,et al. High frequency incipient fault detection for engine bearing components [C]//Proceedings of the ASME Turbo Expo. New York,USA: ASME,2005: 413-427.

[10] BYINGTON C S,ORSAGH R,KALLAPPA P,et al. Recent case studies in bearing fault detection and prognosis [C]//IEEE Aerospace Conference Proceedings. Piscataway,NJ,USA: IEEE,2006: 1656077.

[11] 徐東,徐永成,陳循,等. 基于EMD的灰色模型的疲勞剩余壽命預測方法研究 [J]. 振動工程學報,2011,24(1): 104-110.

XU Dong,XU Yongcheng,CHEN Xun,et al. Residual fatigue life prediction based on grey model and EMD [J]. Journal of Vibration Engineering,2011,24(1): 104-110.

[12] PARZEN E. On estimation of a probability density function and mode [J]. The Annals of Mathematical Statistics,1962,33: 1065-1076.

[13] CAIN J B. An improved probability neural networks and its performance relative to other model [C]//Application of Artificial Neural Networks. Orlando,USA: SPIE Press,1990: 358-359.

[14] FUGATE M L,SOHN H,FARRAR C R. Vibration-based damage detection using statistical process control [J]. Mechanical Systems and Signal Processing,2001,15(4): 707-721.

[15] 符祥,郭寶龍. 圖像插值技術(shù)綜述 [J]. 計算機工程與設(shè)計,2009(1): 141-144.

FU Xiang,GUO Baolong. Overview of image interpolation technology [J]. Computer Engineering and Design,2009(1): 141-144.

[16] SAWALHI N,RANDALL R B,ENDO H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis [J]. Mechanical Systems & Signal Processing,2007,21(6): 2616-2633.

[本刊相關(guān)文獻鏈接]

陳保家,汪新波,嚴文超,等.采用品質(zhì)因子優(yōu)化和子帶重構(gòu)的共振稀疏分解滾動軸承故障診斷方法.2018,52(4):70-76.[doi:10.7652/xjtuxb201804010]

夏平,徐華,馬再超,等.采用改進HVD與Lempel-Ziv復雜性測度的滾動軸承早期損傷程度評估方法.2017,51(6):8-13.[doi:10.7652/xjtuxb201706002]

張俊紅,馬梁,魯鑫,等.機動飛行下擠壓油膜阻尼器對碰摩故障轉(zhuǎn)子系統(tǒng)的影響.2015,49(11):62-70.[doi:10.7652/xjtuxb201511011]

李軍寧,陳渭,謝友柏.采用知識流理論的高速滾動軸承打滑失效試驗臺集成設(shè)計.2015,49(5):87-93.[doi:10.7652/xjtuxb201505014]

唐貴基,王曉龍.參數(shù)優(yōu)化變分模態(tài)分解方法在滾動軸承早期故障診斷中的應用.2015,49(5):73-81.[doi:10.7652/xjtuxb201505012]

易均,劉恒,劉意,等.歪斜安裝對組配軸承轉(zhuǎn)子系統(tǒng)動力學特性影響.2014,48(9):107-111.[doi:10.7652/xjtuxb201409 018]

付新哲,張優(yōu)云,朱永生.滾動軸承故障診斷的案例推理方法.2011,45(11):79-84.[doi:10.7652/xjtuxb201111015]

栗茂林,王孫安,梁霖.利用非線性流形學習的軸承早期故障特征提取方法.2010,44(5):45-49.[doi:10.7652/xjtuxb 201005010]

王曉冬,何正嘉,訾艷陽.滾動軸承故障診斷的多小波譜峭度方法.2010,44(3):77-81.[doi:10.7652/xjtuxb201003016]