采用投影螺旋搜索的改進粒子群算法
高嘉樂,邢清華,李龍躍,范成禮
(空軍工程大學防空反導學院,710051,西安)
受鳥群捕食的行為啟發,Kenney等于1995年提出了粒子群優化(PSO)算法[1-2],這種算法具有收斂速度快、結構簡單等特點,由于它對許多優化問題表現出較高的求解效率而受到國內外廣泛的關注[3-5]。但是在求解高維空間的復雜問題時,PSO算法容易早熟且陷入局部最優,在多峰值函數的求解問題中表現更為明顯。針對這一問題,很多學者對PSO算法進行優化和改進,主要集中在參數調整和與其他智能算法相結合兩個方面。增加隨機搜索范圍和頻率的方式可以避免PSO算法陷入局部最優,采用的方法如模糊邏輯[6]、混沌理論[7]、變化臨域粒子輔助更新[8]等。大部分改進算法將基本PSO算法與全局搜索能力較強的智能算法結合,例如多種群方法[9]、人工蜂群(ABC)算法[10]、布谷鳥算法[11]、采用螺旋樣式的渦流搜索(VS)算法等。
目前,螺旋搜索(SS)主要應用于反潛搜索路徑規劃、磁盤陣列搜索等領域,但在連續函數優化方面應用較少。文獻[12]提出了一種螺旋粒子群搜索算法,采用了一種螺旋樣式的搜索行為以解決PSO早熟問題,這種方法的參數是隨機設置的,并且搜索區域尺寸固定,相當于在一個固定尺度搜索空間中的隨機搜索,雖然可以避免陷入局部最優,但效率不高。與螺旋搜索樣式相似,文獻[13]提出一種渦流樣式的算法,以當前種群個體為中心在一個衰減半徑的區域內進行隨機搜索,盡管搜索范圍衰減,但這種搜索方式仍然是一種無目的的搜索。文獻[14]提出了量子渦流算法,將渦流搜索行為投影到Bloch球面中,投影搜索行為可以有效地避免在搜索后期大范圍的無目的的搜索。
螺旋搜索具有很好的全局搜索能力,但是參數多、后期搜索效率低,因此在連續空間的最優化問題中應用較少。針對上述問題,提出了一種基于投影空間的螺旋搜索的粒子更新算法(SSPSO),并應用于粒子群算法中以解決早熟問題。為了增強算法的尋優能力,引入自適應算子選擇方法和混沌變異策略。仿真實驗表明,本文算法能夠以較少的迭代次數收斂,且具有較高的尋優精度和尋優穩定性。
1 基本粒子群算法
粒子群算法的基本概念源于鳥群捕食行為。在粒子群算法中,每一只鳥看作一個粒子,食物是適應度,頭鳥則是每一代的全局最優解,所有粒子向著全局最優解進行收斂。每個粒子的速度和位置更新公式為
(1)
(2)
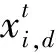
2 基于螺旋搜索的粒子群算法
2.1 螺旋搜索策略
智能算法的搜索方式主要有隨機搜索和個體合作兩種方法。隨機搜索可以分為兩種:一種是全局隨機搜索,這種方法簡單但搜索效率低;另一種是小范圍的隨機擾動,這種方法是在上一代優秀個體周圍進行小范圍的隨機搜索,搜索效率高且特別適用于求解多峰值問題。個體合作通常用于加快收斂,在優秀個體周圍進行搜索容易尋找到更優的個體,但是這種方法也最容易陷入局部最優。受VS算法的啟發,結合上述兩種搜索策略,本文提出了一種新的螺旋搜索方式。
由于搜索行為是建立在螺旋樣式的曲線上,對于螺旋曲線的選擇沒有固定的要求,本文僅以雙曲螺旋線為例
(3)
式中:w是旋轉角度,w∈(-∞,0)∪(0,+∞);θ1和θ2是位置擾動參數,θ1、θ2∈(-1,1)。當w趨近于0時,曲線可以近似看作為一條直線;當w趨近于無窮時,曲線則是呈螺旋的樣式收斂到(0,0)點。依據上述分析,只要旋轉角度不趨近于0,曲線即可呈現螺旋樣式。為了便于計算,選取一個整數作為旋轉角度的下界,本文設w∈(2π,+∞),使收束曲線呈螺旋形狀。
文獻[12]中的螺旋搜索方法采用絕對尺度的螺旋曲線在決策空間搜索,搜索后期依然還有很大的搜索范圍,雖然絕對尺度的螺旋搜索具有全局搜索的功能,但搜索到更好的個體難度較大。受文獻[14]啟發,本文提出了一種相對尺度的搜索,即將搜索投影到一個固定的螺旋曲線的空間中,使得搜索尺度隨著搜索過程的進行而變化,效率更高。
2.2 基于螺旋搜索的粒子更新
依據個體合作策略選擇兩個粒子進行合作,一個是當前粒子xi,另一個在種群中隨機選擇粒子xj。然后在螺旋曲線上隨機選擇一個點(a1,b1)作為xi的投影點,(a1,b1)稱為第一投影點;xj投影到(0,0),(0,0)為第二投影點。假設點(a1,b1)的旋轉角度取值w1,在螺旋曲線上生成一個點作為新個體(a2,b2),(a2,b2)的旋轉角度w2取值公式為
w2=w1+Lπ
(4)
式中:L是角度控制參數。螺旋搜索示意圖如圖1所示。圖1中2個三角點分別是螺旋線的起點和終點,它們的旋轉角度w=2π和w=10π,依據式(3)計算2個點的位置,在圖1中標注為三角點。新粒子在螺旋線的投影為(a2,b2)。當L趨近于+∞時,(a2,b2)趨近于(0,0),(a2,b2)在決策空間映射的個體與(0,0)對應的xj相似度增高。當w趨近于+∞時,螺旋線上點的變化趨于0,此時變異差別極小,搜索能力可以忽略不計。
為了避免對個體周圍進行過度的局部搜索,定義起始點的旋轉角度w1和控制參數L的取值范圍,w1∈(2π,10π)和L∈(0,500)。兩個參數的下限依據旋轉角度w的取值范圍定義。w1主要用于確定第一投影點的位置,是螺旋搜索行為的起點。在實驗過程中發現,w1對于搜索過程影響不大,因此定義w1是(2π,10π)范圍內的隨機數。隨機生成的目的是為了保證每次搜索行為的隨機性,最大限度地避免重復個體的生成。L是螺旋搜索的主要參數,L過大偏重于對第二投影點的周圍進行搜索,L過小偏重全局搜索。在實際的參數測試過程中,L的上界較小時對于搜索影響不大,但是L超過500時,算法的搜索效率下降,因此將其上限設為500。
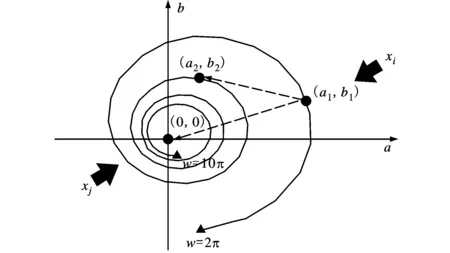
圖1 螺旋搜索示意圖
螺旋搜索每次只選擇粒子的一個維度,即將粒子的一個維度投影到螺旋線(a1,b1)上,得到新生成粒子的兩個候選解
(5)
由式(3)可以看出,當w取值趨于π/2的整數倍時,a或b趨近于0。在求解式(5)之后,兩個候選解可能超出決策空間的范圍,為了避免此類現象發生,選取兩個候選解中速度v較小的解作為粒子的下一代解的速度,速度和粒子位置更新如下式
(6)
(7)
從螺旋搜索粒子更新方式可以看出,螺旋搜索的全局尋優策略的優勢主要有不同維度變異無相關性和反向搜索能力兩方面。對于不同維度變異無相關性來說,每一維度搜索的結果都是不同的,雖然新粒子需要兩個父代個體的信息才能產生,但新粒子的速度方向與兩個父代個體的連線方向沒有直接關系,兩個方向呈現正交關系都是可能的。對于反向搜索能力來說,如果新粒子的投影點(a2,b2)與父代個體(a1,b1)在對角象限上,由式(5)可知,新粒子的速度方向為負,即在決策空間上的位置與xj的方向相反,而速度小于2倍的xi與xj之間的距離。
2.3 基于混沌擾動策略的參數設置
完全隨機搜索是一種相對低效的但是簡單的全局搜索行為,而小概率的擾動可相對高效地提高算法的尋優能力。本文為螺旋搜索行為設置了多個隨機參數,這些參數通過擾動促使搜索行為不重復。本文的隨機擾動參數主要有4個:第一投影點位置參數w1,曲線擾動參數θ1和θ2,以及控制參數L。
為了提高搜索效率,將混沌思想引入螺旋搜索中,選擇經典的Logistic映射[16],計算公式為
zt+1=4zt(1-zt)
(8)
式中:zt∈[0,1]為混沌變量,正整數t為迭代次數。
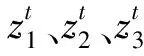
(9)
(10)
(11)
(12)
理論上這種經典的Logistic映射的值域是一個閉區間。為了避免取到參數的邊界值,本文添加參數重新生成機制,即如果參數在混沌變異的過程中產生邊界值,那么隨機取值重新開始混沌變異。
2.4 自適應算子選擇
傳統PSO個體更新策略具有良好的收斂性,但容易陷入早熟;螺旋搜索具有良好的擾動性,能夠提高算法全局尋優能力,但是在收斂速度方面不如傳統PSO的更新策略。本文提出一種自適應算子選擇策略,在搜索階段的初期以較大的概率選擇傳統的PSO粒子更新策略,提高算法的收斂速度,在后期以較大的概率選擇螺旋搜索方式,以避免搜索陷入局部最優。定義算子選擇概率
(13)
式中:T表示最大迭代次數。在自適應算子選擇策略中,首先產生一個隨機數,r3∈(0,1)區間,如果隨機數小于P,則采用傳統PSO更新策略,否則使用螺旋搜索。
2.5 算法描述和分析
下面對算法步驟進行詳細描述。
輸入:加速因子c1和c2、慣性權重因子c0、種群規模N、最大迭代次數T。
輸出:全局最優解pg。
步驟1初始化種群粒子位置和速度;
步驟2計算種群的適應度值,并尋找個體歷史最優解pi和全局最優解pg;
步驟3依據2.4節中的自適應算子選擇策略,生成隨機數r3,如果r3 步驟4使用式(3)和式(4)更新粒子速度與位置,轉至步驟7; 步驟5依據2.3節混沌擾動策略生成螺旋搜索參數; 步驟6使用螺旋搜索更新粒子速度與位置; 步驟7更新個體歷史最優解pi和全局最優解pg; 步驟8迭代終止條件判斷,若滿足,轉至步驟9,否則轉至步驟3; 步驟9輸出全局最優解pg,算法結束。 從文獻[17]選取常用的高維測試函數檢驗本文算法性能,測試函數的名稱、編號、搜索范圍以及理論最優解見表1。其中f1為單峰可分離函數;f2~f5為單峰不可分離函數;f6~f7為多峰不可分離函數;f8~f10為旋轉多峰不可分離函數。 將本文提出的SSPSO算法與基本PSO算法、VS算法[13]、量子衍生渦流(QIVS)算法[14]對比。其中,PSO的c0設為0.729,學習因子c1和c2設為0.747,VS和QIVS的參數采用自適應方法生成,無需設置。在仿真中,種群規模N=100,最大迭代次數T=200,測試函數維度n=30。4種算法在10個測試函數中運行30次,將每種算法在每個測試函數上運行結果的平均值、標準差和平均運行時間trun進行比較。仿真實驗運行環境為64位Win7操作系統,CPU為Core i5 3.30 GHz,RAM為4 GB。 表1 測試函數描述 4種算法的對比結果見表2,其中黑體的數據為對比結果最優值。從表2中可以看出,本文提出的算法性能良好,10個測試函數中,有8個測試函數得到結果最好。QIVS算法比PSO算法和VS算法的運行結果好,但與SSPSO算法相比只在f5和f8上獲得了最好結果,且QIVS算法的平均值與SSPSO算法的結果在同一個數量級。比較PSO算法和VS算法的平均值,PSO算法總體上略優于VS算法。VS算法的不定向變異雖然不容易陷入局部最優,但是其搜索效率是最低的,因此在有限的迭代次數中表現較差。 圖2給出了4種算法在迭代過程中的收斂曲線。VS算法整體表現最差,在測試函數f1、f4~f10都是在100次迭代以后才收斂,而且尋優能力相對較弱。PSO算法具有較好的性能,表現出較好的尋優能力,在f1~f3、f5和f10能夠以較少的迭代次數收斂。在收斂速度方面,PSO算法弱于QIVS算法和SSPSO算法,在尋優精度方面,PSO算法在f4、f6、f9表現明顯不如QIVS算法和SSPSO算法。 (a)f1 (b)f2 (c)f3 (d)f4 (e)f5 (f)f6 (g)f7 (h)f8 (i)f9 (j)f10 表2 4種算法運行結果的平均值和標準差對比 PSO、QIVS、SSPSO 3個算法在f4、f6、f7和f94個測試函數中尋優性能差異明顯,其中SSPSO算法能夠以較少的迭代次數收斂,且具有明顯優于其他3種算法的尋優能力。 表3給出了4種算法在10個測試函數運行時的平均運行時間。PSO算法和VS算法的運行時間在同一個量級,但是PSO算法比VS算法略好。而本文算法和QIVS算法則相對花費較長時間。 表3 4種算法平均運行時間對比 為解決高維空間中復雜多峰函數的優化問題,本文提出了基于投影空間的螺旋搜索粒子更新方式,并引入自適應算子選擇和混沌策略,提出了投影螺旋搜索粒子群算法。通過測試函數的實驗分析,本文提出的算法在性能上優于傳統PSO算法,具有較高的求解精度,能夠以較少的迭代次數收斂,適合于求解具有連續空間復雜多峰值特點的工程應用問題。下一步工作主要采用大量的仿真實驗和逆向推導的方法優化算法參數設置以及研究不同的投影點選取對于搜索的影響。 參考文獻: [1] KENNEDY J,EBERHART R C. Particle swarm optimization [C]//Proceedings of the IEEE International Conference on Neural Networks. Piscataway,NJ,USA: IEEE,1995: 1942-1948. [2] EBERHART R,KENNEDY J. A new optimizer using particle swarm theory [C]//Proceedings of the International Symposium on Micro Machine and Human Science. Piscataway,NJ,USA: IEEE,1995: 39-43. [3] 張卿祎,王興偉,黃敏. 基于PSO和SA混合優化的智能容錯QoS路由機制 [J]. 東北大學學報(自然科學版),2017,38(3): 325-330. ZHANG Qingyi,WANG Xingwei,HUANG Min. An intelligent fault-tolerant QoS routing mechanism based on PSO and SA hybrid optimization [J]. Journal of Northeastern University(Natural Science),2017,38(3): 325-330. [5] WITEK H A,CHOU C P,MAZUR G,et al. Automatized parameterization of the density-functional tight-binding method: II Two-center integrals [J]. Journal of the Chinese Chemical Society,2016,63(1): 57-68. [6] OLIVAS F,VALDEZ F,CASTILLO O,et al. Dynamic parameter adaptation in particle swarm optimization using interval type-2 fuzzy logic [J]. Soft Computing,2016,20(3): 1057-1070. [7] XU Xiaolong,RONG Hanzhong,TROVATI M,et al. CS-PSO: chaotic particle swarm optimization algorithm for solving combinatorial optimization problems [J]. Soft Computing,2016,2018(22): 1-13. [8] SUN Wei,LIN Anping,YU Hongshan,et al. All-dimension neighborhood based particle swarm optimization with randomly selected neighbors [J]. Information Sciences,2017,405(9): 141-156. [9] PORNSING C,SODHI M S,LAMOND B F. Novel self-adaptive particle swarm optimization methods [J]. Soft Computing,2016,20(9): 3579-3593. [10] LI T H S,LIN C J,KUO Pinghuan,et al. Grasping posture control design for a home service robot using an ABC-based adaptive PSO algorithm [J]. International Journal of Advanced Robotic Systems,2016,13(10): 1-15. [11] LI Xiangtao,YIN Minghao. A particle swarm inspired cuckoo search algorithm for real parameter optimization [J]. Soft Computing,2016,20(4): 1389-1413. [12] 滕弘飛,張英男. 螺旋粒子群優化算法的研究簡報 [EB/OL]. (2012/4/10)[2017-06-23]. http: //www. docin.com/p-379958059.html. [14] 李盼池,盧愛平. 量子衍生渦流搜索算法 [J]. 控制與決策,2015,31(6): 990-996. LI Panchi,LU Aiping. Quantum-inspired vortex search algorithm [J]. Control and Decision,2015,31(6): 990-996. [15] CLERC M,KENNEDY J. The particle swarm: explosion,stability and convergence in a multi-dimensional complex space [J]. IEEE Transactions on Evolutionary Computation,2002,6(2): 58-73. [16] LIU Bo,WANG Liang,JIN Yihui,et al. Improved particle swarm optimization combined with chaos [J]. Chaos,Solitons and Fractals,2005,25(5): 1261-1271. [17] 紀震,廖惠連,吳青華. 粒子群算法及應用 [M]. 北京: 科學出版社,2009: 73-113.3 實驗分析
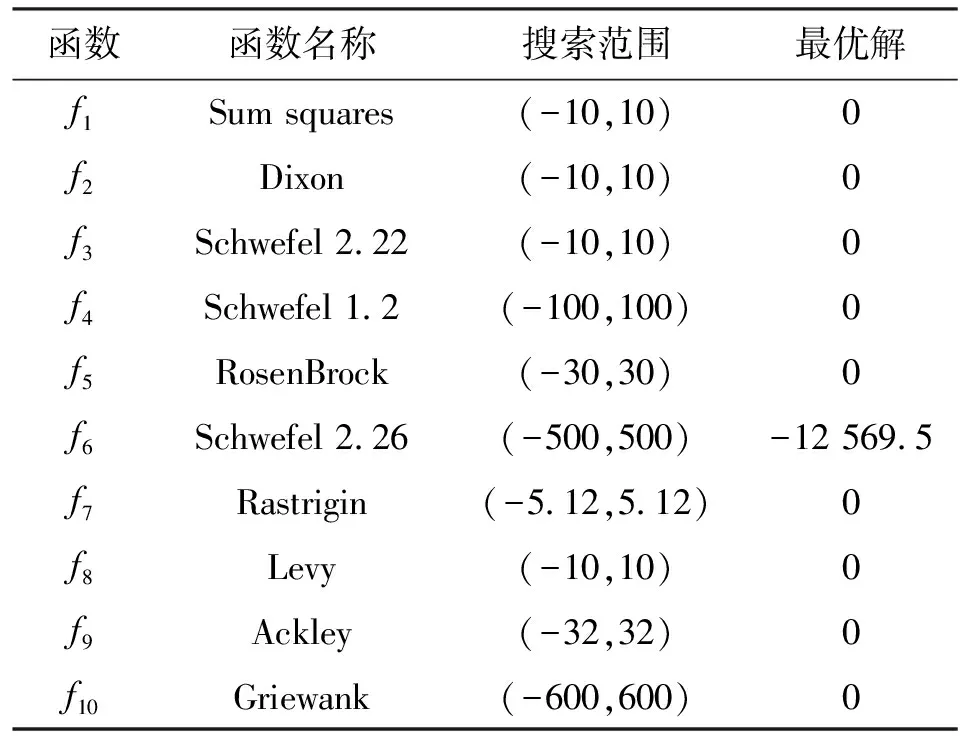
3.1 測試函數及參數設置
3.2 測試和結果分析
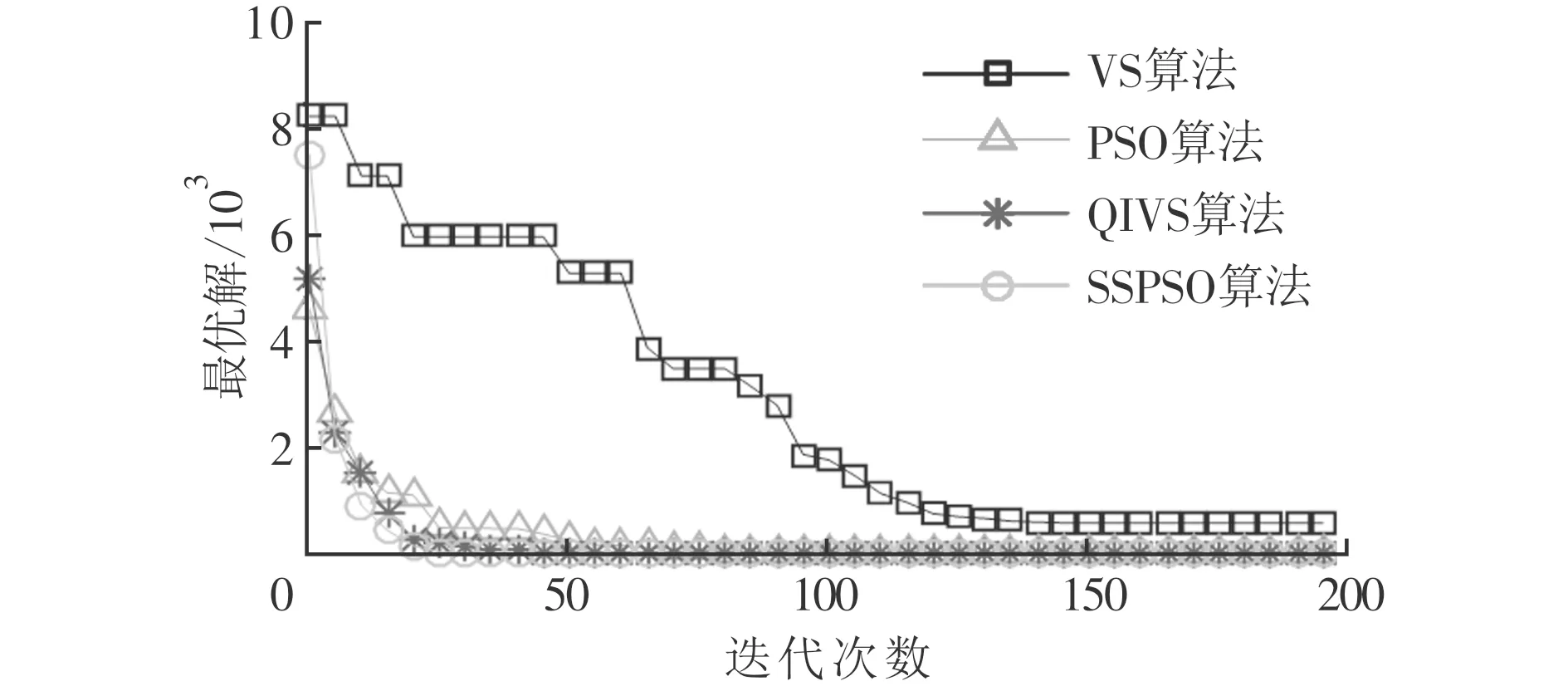
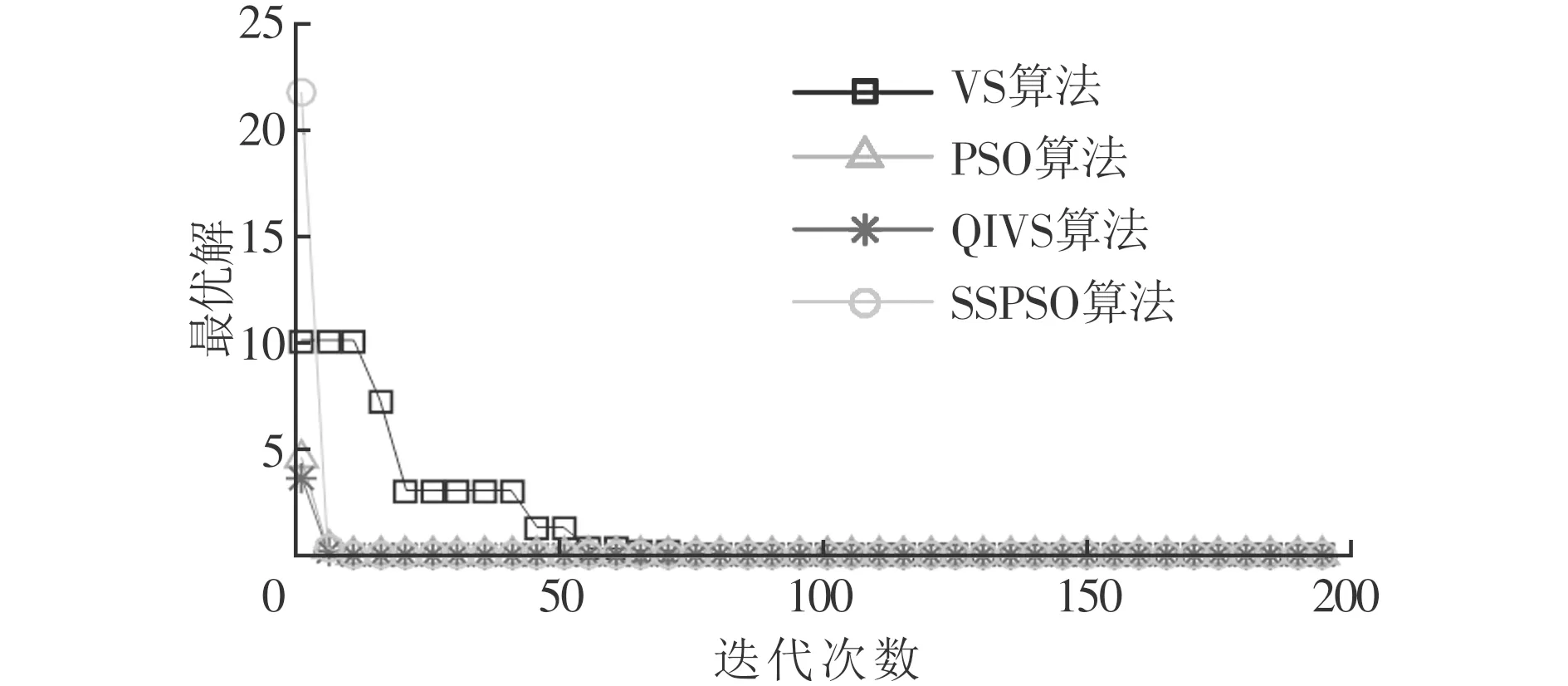

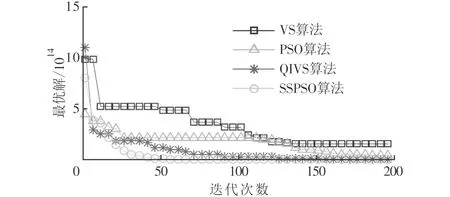
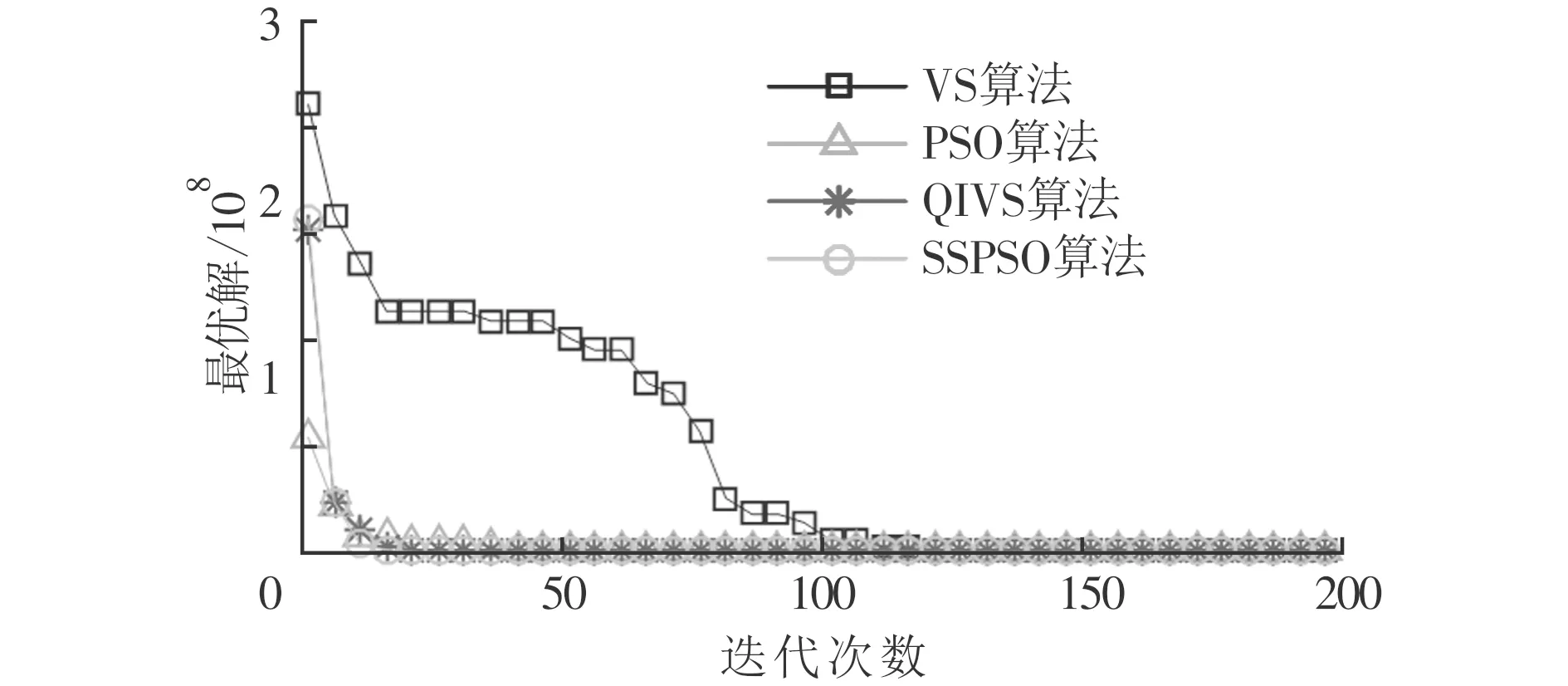
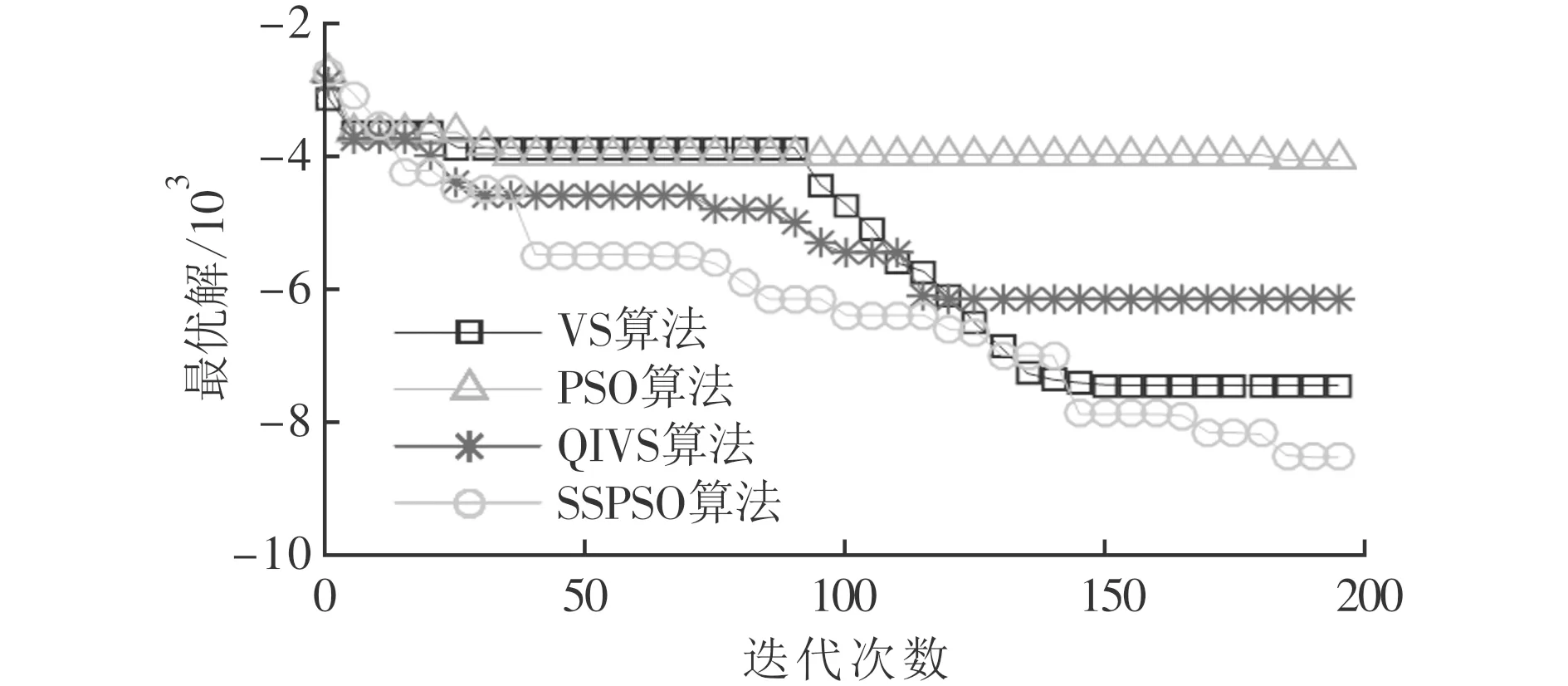
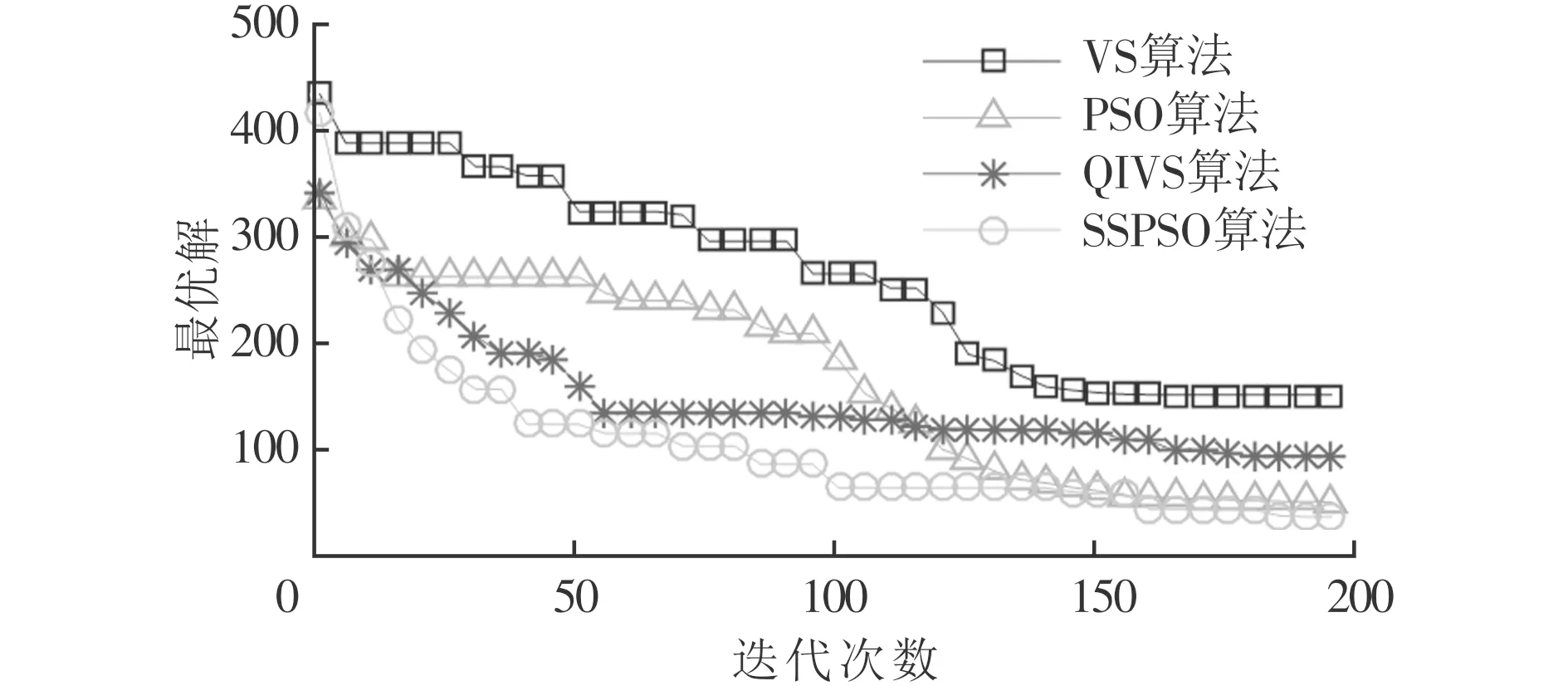
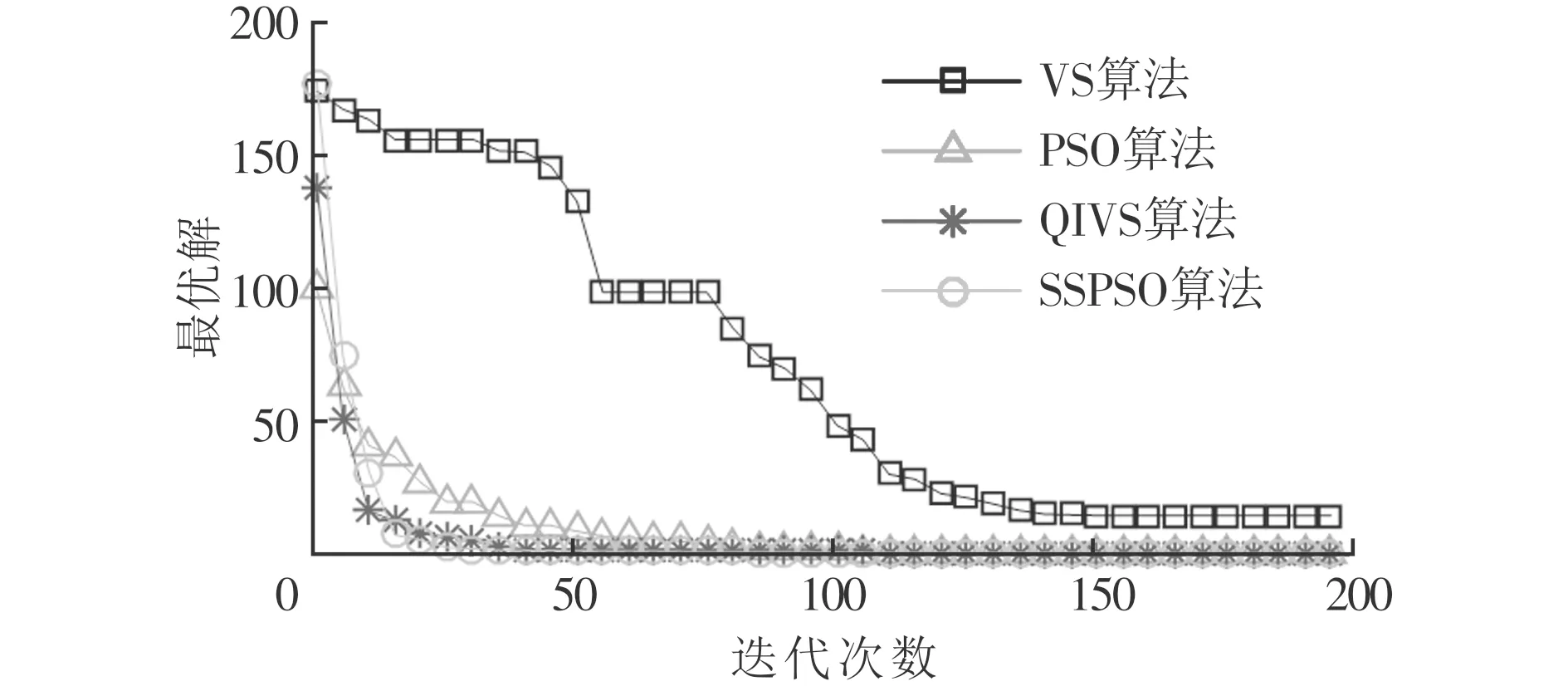
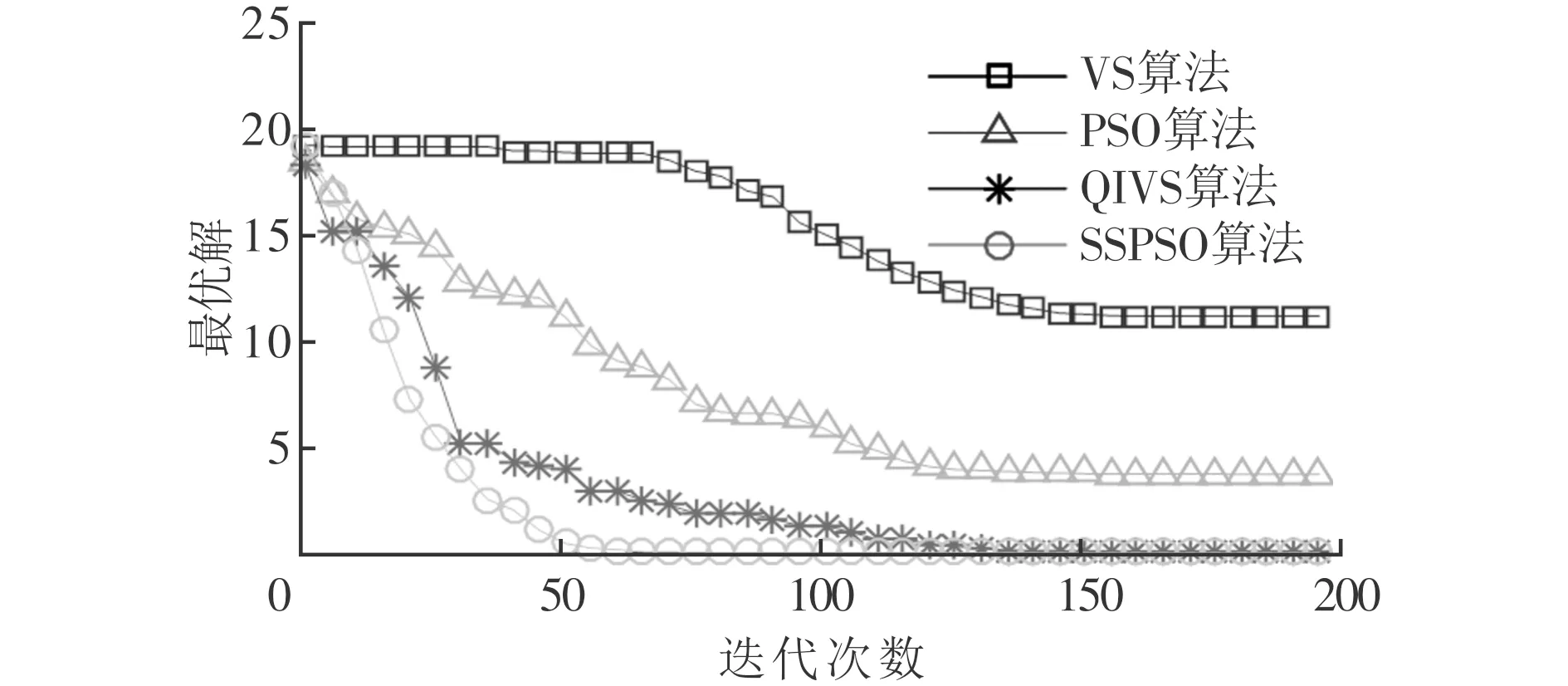
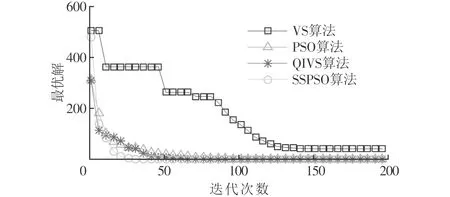
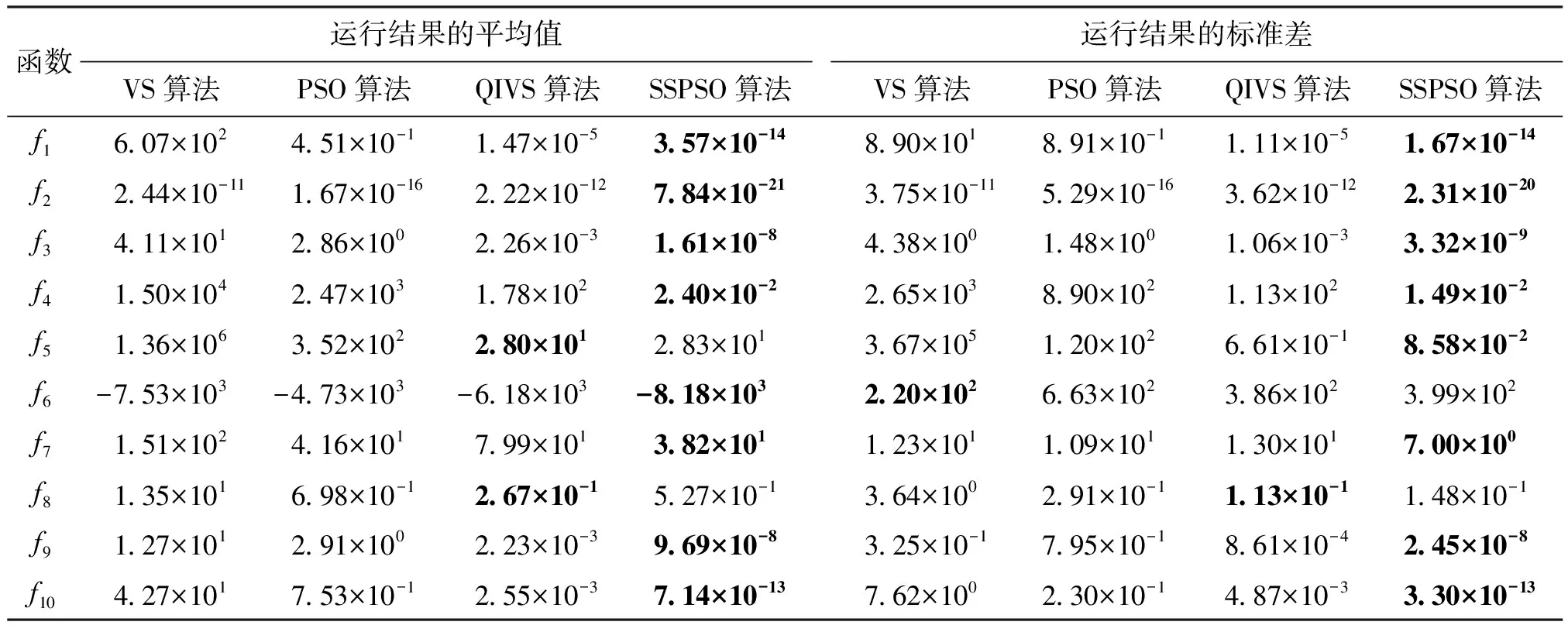
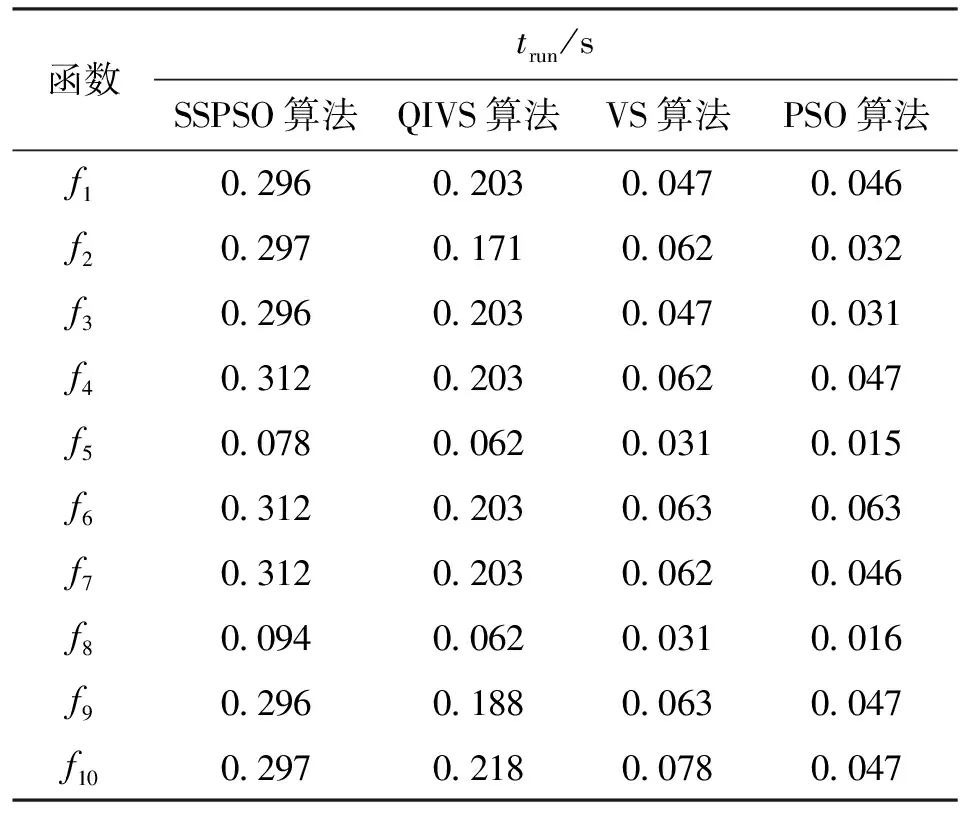
4 結 論

