迷宮齒彎曲磨損時密封泄漏特性和 轉子動力特性系數研究

陳堯興,李志剛,晏鑫,李軍,2

(1.西安交通大學能源與動力工程學院,710049,西安; 2.先進航空發動機協同創新中心,100191,北京)

迷宮密封由于其可靠的封嚴性能、相對較低的制造成本和易于安裝維護、非接觸特性允許更高轉速運行的特點而在透平機械通流動靜間隙控制中得到廣泛應用。當透平機械在啟動、停機和熱重啟過程中,迷宮密封靜子件與轉子件之間容易發生碰磨從而使得封嚴性能退化[1],同時引起密封氣流激振轉子動力特性發生改變。如果碰磨過程中轉子對迷宮齒存在強烈的沖擊,那么任何金屬材料加工成的迷宮齒均將存在不同程度的彎曲[2-3]。

目前,國內外開展密封彎曲磨損的研究很少。Xu等率先研究了迷宮齒彎曲后曲率、彎曲長度以及彎曲后密封間隙對密封泄漏量的影響,指出彎曲后迷宮齒徑向間隙增加是密封泄漏量增加的主要原因[2-3];Yan等對迷宮齒彎曲磨損后密封的傳熱特性進行了研究,發現彎曲角度對轉子面的換熱基本沒有影響,但卻顯著增強了密封靜子面的換熱性能[4]。

科研人員采用實驗測量和數值模擬的方法研究了迷宮密封幾何結構對其轉子動力特性系數的影響規律。Mortazavi等研究了轉子面帶凹槽的液體環形密封的泄漏特性與轉子動力特性,指出轉子面上開設凹槽會使得密封轉子穩定性降低,但大壓差條件下密封封嚴性能明顯增強,同時指出粗糙度是準確預測泄漏量以及剛度系數的重要參數[5];Mehta等對比分析了直通式迷宮密封、傾斜式迷宮密封的泄漏量與轉子動力特性系數,發現迷宮齒向高壓方向傾斜能夠使泄漏量減少10%,但低進口預旋條件下不會改變密封轉子動力特性系數[6];賈興運等對T型交錯式迷宮密封與普通交錯式迷宮密封的穩定性進行了研究,發現與普通交錯式迷宮密封相比,T型交錯式迷宮密封能夠強化Lomakin效應,產生徑向向內的徑向力,避免加劇轉子振動從而使得轉子穩定性增強[7];李志剛等研究了轉子偏心對密封靜態動力特性的影響,指出轉子偏心率增加會使得密封正交叉剛度增加,從而易誘發轉子失穩[8]。

目前已經開展了很多密封幾何結構改變對轉子動力特性影響的研究,然而迷宮齒彎曲磨損對密封轉子動力特性影響的研究尚未開展,因此本文參考Ertas等的迷宮密封幾何結構參數[9],設計了彎曲前迷宮齒徑向間隙為0.3 mm和3種不同彎曲程度下迷宮齒徑向間隙分別為0.4、0.5、0.6 mm的迷宮齒密封結構,并采用多頻橢圓渦動模型預測方法[10]研究了密封泄漏量和轉子動力特性系數,同時計算了未彎曲下迷宮齒徑向間隙為0.4、0.5、0.6 mm時密封泄漏量以進行對比分析。本文評估密封彎曲程度對密封泄流量以及穩定性的影響,為迷宮密封彎曲磨損運行狀態下的性能分析提供了參考。

1 計算模型和數值方法

圖1給出了迷宮齒彎曲磨損時迷宮密封幾何結構。圖2給出了迷宮齒彎曲磨損模型。需要指出的是,本文采用的完全彎曲模型在以下2點假設的前提下成立[2-3]:迷宮齒中心線彎曲后是一條圓弧;對于彎曲前迷宮齒上任意截面,彎曲后齒厚不發生改變。

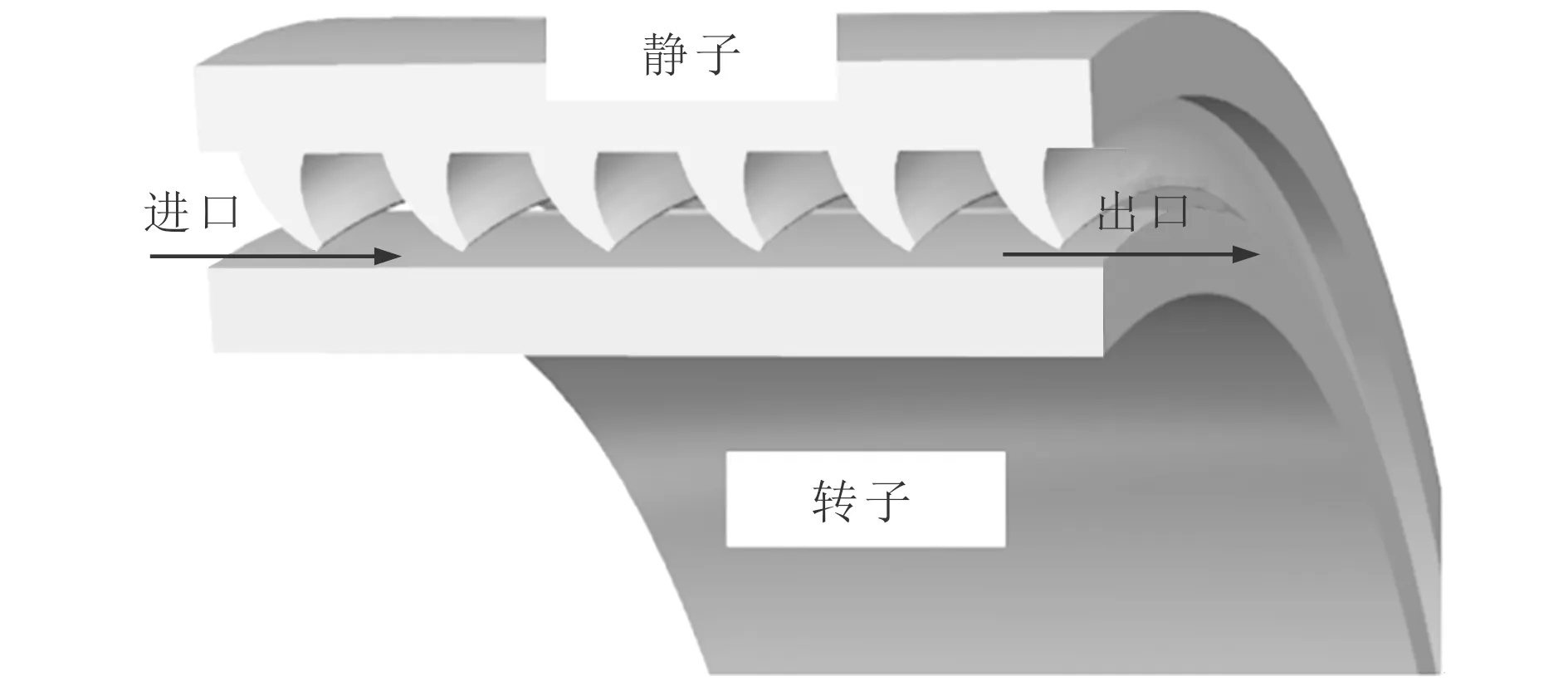
圖1 迷宮齒彎曲磨損時迷宮密封幾何結構

圖2 迷宮齒彎曲磨損模型

根據假設1可知,迷宮齒彎曲前齒高Lt與彎曲后迷宮齒中心線彎曲半徑Rb、彎曲角度β滿足下式

Rbβ=Lt

(1)

迷宮齒彎曲前任意截面上齒厚ω與高度l(l為該截面到齒根的距離)滿足關系

ω=Wr-(Wr-Wt)l/Lt

(2)

式中:Wr為齒根厚度;Wt為齒頂厚度。

根據假設2可知,那么迷宮齒彎曲后任意位置處齒厚ω與角度δ的關系為

ω=Wr-(Wr-Wt)Rbδ/Lt

(3)

迷宮齒彎曲后齒根到迷宮齒前緣任意位置處y方向上的距離為

y=(Rb+ω/2)sinδ

(4)

需要注意的是,迷宮齒彎曲后齒根到迷宮齒前緣在y方向上的最大距離與腔室高度H、彎曲后密封間隙Cab存在以下關系

ymax=H-Cab

(5)

迭代求解式(1)～(5)可求得迷宮齒彎曲后的半徑與角度。

根據Ertas等公布的幾何數據[9]可知,彎曲前密封腔室高度H為4.01 mm、間隙為0.3 mm,齒高Lt為3.71 mm,齒根厚度為2.29 mm,齒頂厚度為0.3 mm;選取彎曲后迷宮齒徑向間隙分別為0.4、0.5、0.6 mm,則根據上述彎曲模型可得迷宮齒中心線彎曲半徑與彎曲角度見表1。

根據式(1)～(5)可以得知,當彎曲后迷宮齒的徑向間隙確定后,迷宮齒中心線的曲率以及彎曲角度就能唯一確定,且迷宮齒中心線的曲率和彎曲角度隨彎曲后密封徑向間隙增加而增加,因此彎曲后的密封徑向間隙可以表征出迷宮齒的彎曲程度。

表1 彎曲迷宮齒不同間隙下中心線彎曲半徑與彎曲角度

圖3給出了迷宮齒彎曲磨損時密封三維網格示意圖。表2給出了迷宮齒彎曲前后部分幾何參數和計算邊界條件。

圖3 迷宮齒彎曲磨損后密封三維網格示意圖

表2 彎曲磨損前后迷宮齒幾何參數和計算邊界條件

采用基于動網格技術和多頻橢圓渦動模型的非定常數值方法[10]求解unsteady Reynolds-averaged Navier-Stokes (URANS)方程,計算分析了彎曲前迷宮齒間隙為0.3 mm以及彎曲后3種不同迷宮齒彎曲程度下迷宮齒徑向間隙分別為0.4、0.5、0.6 mm時的密封泄漏量以及轉子動力特性系數,同時計算了未彎曲下迷宮齒徑向間隙為0.4、0.5、0.6 mm時密封泄漏量以進行參考分析。表3給出了迷宮密封轉子動力特性系數計算的數值方法和渦動模型參數。在偏心渦動條件下,密封轉子在繞轉子中心C旋轉的同時,假定圍繞靜子中心o作周期性橢圓渦動。圖4給出了轉子橢圓渦動軌跡模型示意圖。針對本文所采用的多頻橢圓渦動模型預測方法的實驗驗證可參考文獻[10-11]。

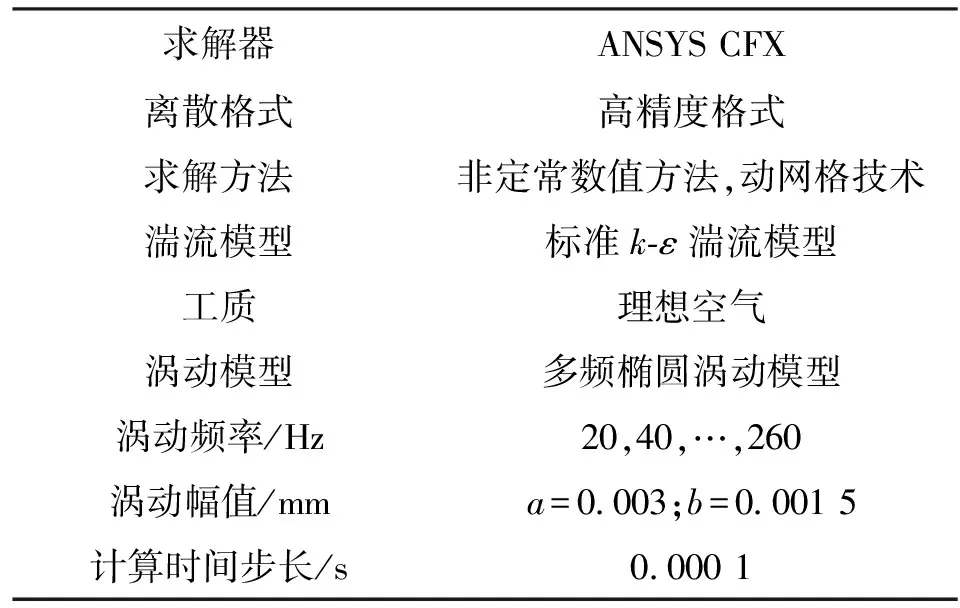
表3 轉子動力特性系數計算方法與渦動模型參數

注:a和b分別為橢圓軌跡的長軸和短軸。

(a)x方向激勵 (b)y方向激勵C:轉子中心(自旋中心) o:靜子中心(渦動中心)圖4 轉子橢圓渦動軌跡模型示意圖

圖5 不同網格數下迷宮密封交叉剛度與直接阻尼隨渦動頻率的變化曲線

圖5給出了迷宮齒徑向間隙為0.6 mm時3種網格數下交叉剛度與直接阻尼隨渦動頻率的變化曲線。可以發現,交叉剛度受網格節點數的影響較小,密封直接阻尼在低頻渦動條件下受網格節點數的影響較大,且當網格節點數從477.1萬增加至700.2萬時,密封直接阻尼變化幅度小于3.8%,可認為已經滿足網格無關性要求,因此本文密封網格節點數選為477.1萬。

2 結果分析與討論

2.1 迷宮齒彎曲磨損時的泄漏量

圖6給出了彎曲磨損條件下迷宮密封泄漏量隨迷宮齒徑向間隙的變化曲線。在彎曲磨損條件下,當迷宮齒徑向間隙分別從0.3 mm增加至0.4 mm、0.4 mm增加至0.5 mm、0.5 mm增加至0.6 mm時,通過密封的泄漏量增幅分別為彎曲前泄漏量的44.2%、101.1%、161.3%,這種泄漏量的增幅是密封徑向間隙增加與迷宮齒彎曲曲率增加共同作用的結果。同時可以發現:迷宮齒未彎曲時,通過密封的泄漏量隨徑向間隙增加而線性增加;在相同徑向間隙條件下,迷宮齒彎曲增加了密封泄漏量,即當迷宮齒徑向間隙為0.5 mm時,迷宮齒彎曲使得密封泄漏量增加3.9%;當迷宮齒徑向間隙為0.6 mm時,迷宮齒彎曲使得密封泄漏量增加6.1%,這與文獻[2-3]中迷宮齒彎曲曲率對泄漏量影響的結論一致。

圖6 密封泄漏量隨迷宮齒徑向間隙的變化曲線

圖7 彎曲磨損條件下第1個迷宮齒間隙內軸向速度沿徑向的分布

為了更好地闡述迷宮齒彎曲曲率對泄漏量的影響,選取彎曲條件下距第一個齒頂前緣點軸向距離為0.15 mm處和未彎曲條件下第一個齒中心處軸向速度沿徑向的分布進行分析。圖7、圖8分別給出了彎曲磨損條件下、未彎曲條件下第1個迷宮齒間隙內軸向速度沿徑向歸一化位置y*的分布。需要指出的是,歸一化徑向位置y*存在限制條件

y*=(y-r0)/Cr,y≤r0+Cr

(6)

式中:r0為轉子半徑。

縮流面積是衡量密封泄漏量的重要指標[12]。相同密封間隙條件下,縮流面積越小,通過密封的泄漏量越少。對于迷宮齒在靜子件上的迷宮密封而言,密封間隙內縮流面積是指第一個齒間隙內單位厚度上從轉子面到軸向速度最大位置處的徑向距離。對比分析圖7和圖8可以發現,迷宮齒未彎曲磨損時,靠近迷宮齒頂部均存在回流區,且增加密封間隙并不會改變密封歸一化后的縮流面積。隨著迷宮齒型線彎曲曲率增加,迷宮齒尖處流體速度與徑向的夾角增大,徑向速度分量與軸向速度分量的比值降低,使得密封入口壓縮效應(流體流過密封間隙后的縮流面積小于真實的密封間隙面積)逐漸減弱,歸一化后的縮流面積逐漸增加,進而使得在相同迷宮齒徑向間隙條件下,通過迷宮齒彎曲后的密封泄漏量與未彎曲時相比增大,且隨著徑向間隙增加,這種差異更加顯著。

2.2 迷宮齒彎曲磨損時的轉子動力特性系數

圖9給出了彎曲磨損條件下密封直接剛度隨渦動頻率的變化曲線。可以發現:與迷宮齒未彎曲時相比,迷宮齒彎曲磨損均使得密封直接剛度增大,即迷宮齒彎曲磨損使得轉子系統臨界轉速增大,對于運行轉速低于臨界轉速的轉子系統而言,迷宮齒彎曲磨損有利于避免轉子系統發生共振;隨著迷宮齒彎曲后密封徑向間隙增加,密封直接剛度逐漸增加,但增加幅度逐漸降低,當彎曲后迷宮齒徑向間隙分別從0.3 mm增加至0.4 mm、0.4 mm增加至0.5 mm、0.5 mm增加至0.6 mm時,密封直接剛度分別增加56.7%～110.1%、29.9%～32.2%、3.4%～6.3%。

圖10給出了彎曲磨損條件下密封交叉剛度隨渦動頻率的變化曲線。可以發現,迷宮齒未彎曲或者彎曲情況下,密封均具有負交叉剛度Kxy,即當彎曲后迷宮齒徑向間隙小于0.6 mm時,迷宮齒彎曲后增加迷宮齒徑向間隙不會改變密封交叉剛度的正負號。根據激振力與轉子動力特性系數的關系[6]可知,負交叉剛度Kxy將產生一個與轉子渦動方向相反的切向激振力,從而起到抑制轉子失穩的作用。迷宮齒未彎曲時密封具有最小的負交叉剛度Kxy,當迷宮齒彎曲后迷宮齒徑向間隙分別從0.3 mm增加至0.4 mm、0.4 mm增加至0.5 mm、0.5 mm增加至0.6 mm時,密封負交叉剛度Kxy分別增加26.6%～32.0%、32.3%～35.3%、35.0%～38.2%,同時表明抑制氣流誘發轉子失穩的能力減弱。

圖10 迷宮密封交叉剛度隨渦動頻率的變化曲線

圖11 迷宮密封直接阻尼隨渦動頻率的變化曲線

圖11給出了彎曲磨損條件下密封直接阻尼隨渦動頻率的變化曲線。可以發現,迷宮齒未彎曲或者彎曲情況下,密封均具有正直接阻尼,根據激振力與轉子動力特性系數的關系[6]可知,正直接阻尼將產生一個與轉子渦動方向相反的切向激振力,同樣起到抑制轉子失穩的作用;迷宮齒彎曲磨損使得密封直接阻尼降低,且隨著彎曲后迷宮齒徑向間隙分別從0.3 mm增加至0.4 mm、0.4 mm增加至0.5 mm、0.5 mm增加至0.6 mm時,密封直接阻尼分別降低1.1%～5.1%、7.3%～8.0%、10.4%～12.3%,即抑制轉子失穩的能力隨迷宮齒彎曲后徑向間隙增加而減弱。

圖12給出了彎曲磨損條件下密封交叉阻尼隨渦動頻率的變化曲線。當渦動頻率大于100 Hz時,密宮齒未彎曲時密封具有最大的交叉阻尼Cxy,且隨著迷宮齒彎曲后徑向間隙增加,密封交叉阻尼逐漸降低。

圖12 迷宮密封交叉阻尼隨渦動頻率的變化曲線

綜合考慮交叉剛度與直接阻尼對轉子穩定性的影響,定義有效阻尼如下

Ceff=Cxx-Kxy/Ω

(7)

圖13給出了彎曲磨損條件下密封有效阻尼隨渦動頻率的變化曲線。迷宮齒未彎曲或者彎曲情況下,密封均具有正有效阻尼,即在該運行工況下密封腔室內的氣流激振力不會引起轉子失穩;隨著迷宮齒彎曲后徑向間隙增加,在密封交叉剛度Kxy增加和直接阻尼降低共同作用下,密封有效阻尼逐漸降低,密封轉子穩定性減弱,也就是說,如果密封運行工況改變引起轉子失穩,例如密封進口段存在正預旋等,那么最先發生轉子失穩的一定是迷宮齒彎曲后徑向間隙最大的密封件。

圖13 迷宮密封有效阻尼隨渦動頻率的變化曲線

2.3 迷宮齒彎曲磨損時轉子面上氣流激振力

圖14給出了在x方向激勵和T=0.1 s條件下迷宮密封轉子面上由黏性力與不平衡壓力產生的徑向力與切向力。轉子面上不平衡壓力產生的徑向力Fr與切向力Ft定義如下

(8)

(9)

式中:R為轉子半徑;t為密封長度。

圖14 x方向激勵和T=0.1 s條件下迷宮密封轉子面上徑向力與切向力

可以發現:隨著密封彎曲后徑向間隙增加,轉子面上由不平衡壓力產生的徑向力與切向力均為負值,且徑向力隨彎曲后密封間隙增加而降低,切向力隨彎曲后密封間隙增加而增加;轉子表面上由黏性力產生的徑向力與切向力不受彎曲后密封間隙的影響,表明迷宮齒彎曲后密封腔室內的氣流激振力變化是由密封彎曲結構改變使得腔室內周向非平衡壓力變化所引起的。根據力-位移方程可知,此時密封直接剛度為正值且隨彎曲后密封間隙增加而增加(忽略交叉阻尼對徑向力的影響),有效阻尼為正值且隨彎曲后密封間隙增加而降低,這與圖9、圖13的分析一致。

3 結 論

透平機械在啟動、停機和熱重啟過程中,迷宮齒與轉軸間容易發生碰磨導致迷宮齒彎曲磨損,進而引起迷宮密封性能退化。論文數值研究了密封彎曲磨損程度對密封泄漏特性和轉子動力特性的影響特性,得到如下結論:

(1)迷宮齒彎曲磨損時,當迷宮齒徑向間隙分別從0.3 mm增加至0.4 mm、0.4 mm增加至0.5 mm、0.5 mm增加至0.6 mm時,迷宮密封的泄漏量較未彎曲磨損時分別增加44.2%、101.1%、161.3%,這種泄漏量的變化是迷宮齒徑向間隙增加與迷宮齒彎曲曲率增加共同作用的結果。

(2)迷宮齒未彎曲磨損時,迷宮密封的泄漏量隨徑向間隙增加而線性增加;迷宮齒彎曲曲率增加削弱了密封的入口壓縮效應,增加了密封歸一化后的縮流面積,導致迷宮密封的泄漏量增加,當徑向間隙為0.6 mm時,迷宮齒彎曲磨損引起密封泄漏量增加6.1%。

(3)迷宮齒彎曲磨損時,隨著迷宮齒彎曲后迷宮齒徑向間隙增加,迷宮密封直接剛度逐漸增加;對于運行轉速低于臨界轉速的轉子系統而言,迷宮齒彎曲磨損能夠提高轉子系統臨界轉速,從而有利于避免轉子系統發生共振;密封交叉剛度大小與直接阻尼隨彎曲后密封徑向間隙增加而降低,從而使得密封有效阻尼降低,不利于轉子系統的安全穩定運行。

參考文獻:

[1] GHASRIPOOR F,TURNQUIST N A. Wear prediction of strip seals through conductance [C]//Proceedings of the 2004 ASME Turbo Expo. New York,USA: ASME,2004: 331-337.

[2] XU J,AMBROSIA M S,RHODE D L. Effect of tooth bending damage on the leakage of straight-through labyrinth seals [C]//Proceedings of the 2005 ASME Fluids Engineering Division Summer Meeting. New York,USA: ASME,2005: 119-124.

[3] XU J. Effects of operating damage of labyrinth seal on seal leakage and wheelspace hot gas ingress [D]. Texas,USA: Texas A and M University,2006: 45-65.

[4] YAN X,LEI L,LI J,et al. Effect of bending and mushrooming damages on heat transfer characteristic in labyrinth seals [J]. ASME Journal of Engineering for Gas Turbines and Power,2013,136(4): 041901.

[5] MORTAZAVI F,PALAZZOLO A. Cfd-based prediction of rotordynamic performance of smooth stator-grooved rotor (ss-gr) liquid annular seals [C]//Proceedings of the 2017 ASME Turbo Expo. New York,USA: ASME,2017: V07AT34A007.

[6] MEHTA N J,CHILDS D W. Measured comparison of leakage and rotordynamic characteristics for a slanted-tooth and a straight-tooth labyrinth seal [J]. ASME Journal of Engineering for Gas Turbines and Power,2014,136(1): 012501.

[7] 賈興運,徐國印,張海,等. 轉子振動對T型交錯式迷宮密封性能影響 [J]. 推進技術,2017,38(6): 1370-1378.

JIA Xingyun,XU Guoyin,ZHANG Hai,et al. Effects of rotor vibration on T type labyrinth seal performance [J]. Journal of Propulsion Technology,2017,38(6): 1370-1378.

[8] 李志剛,陳堯興,李軍. 高偏心率下旋轉密封泄漏特性和靜態動力特性研究 [J]. 西安交通大學學報,2017,51(7): 1-7.

LI Zhigang,CHEN Yaoxing,LI Jun. Investigation on the leakage and static dynamic characteristics of rotating seals at high eccentricity ratios [J]. Journal of Xi’an Jiaotong University,2017,51(7): 1-7.

[9] ERTAS B H,DELGADO A,VANNINI G. Rotordynamic force coefficients for three types of annular gas seals with inlet preswirl and high differential pressure ratio [J]. ASME Journal of Engineering for Gas Turbines and Power,2012,134(4): 042503.

[10] LI Z,LI J,YAN X. Multiple frequencies elliptical whirling orbit model and transient RANS solution approach to rotordynamic coefficients of annual gas seals prediction [J]. Journal of Vibration and Acoustics,2013,135: 031005.

[11] 陳堯興,李志剛,晏鑫,等. 迷宮齒蘑菇型磨損時密封泄漏特性和轉子動力特性系數研究 [J]. 西安交通大學學報,2018,52(1): 40-46.

CHEN Yaoxing,LI Zhigang,YAN Xin,et al. Investigations on the leakage characteristics and rotordynamic coefficients of labyrinth seal with mushroom-shaped tooth wear [J]. Journal of Xi’an Jiaotong University,2018,52(1): 40-46.

[12] DOGU Y,SERT?AKAN M C,BAHAR A S,et al. Computational fluid dynamics investigation of labyrinth seal leakage performance depending on mushroom-shaped tooth wear [J]. ASME Journal of Engineering for Gas Turbines and Power,2016,138(3): 032503.