壓縮式冷水機組節能優化研究

溫海棠,吳愛國,尚羽佳

(天津大學電氣自動化與信息工程學院,300072,天津)

作為中央空調系統的核心部分,冷水機組能耗在中央空調系統中比重較大,其中約50%～60%用于制冷機組產生冷量,20%～30%用于冷凍水與冷卻水的輸配。因此,降低冷水機組能耗是建筑節能工作的重要內容[1]。

目前,很多學者對冷水機組進行了建模與工作點優化計算,以實現機組節能運行,很多先進的建模方法和智能優化算法也已引入到冷水機組優化設計中。文獻[2]基于最小二乘法建立了冷水機組在線模型;文獻[3]以總能耗為目標函數對冷水機組進行了負荷的優化分配;文獻[4]建立了較為精確的冷水機組機理模型,并獲得了不同熱負荷下系統的優化設定值;文獻[5]采用簡化性能指標計算冷卻水溫度的優化設定點，在室外溫度大范圍變化工況下可以取得4%以上的節能效果;文獻[6]建立了制冷機組、水泵和冷卻塔等裝置的簡化數學模型，并在此基礎上得到了冷凍水和冷卻水的優化設定點，使系統整體能耗減少約0.73%～2.55%;文獻[7]采用人工神經網絡建立機組模型，并采用粒子群算法與逆神經網絡結合的方法優化機組控制參數；文獻[8]建立了機組能耗模型,并利用遺傳算法進行負荷最優分配以及冷凍水溫度優化設定;文獻[9]采用一種混合穩態機理模型描述冷水機組各變量的相互關系,通過遺傳算法求取系統的優化設定值,在此基礎上,采用分散優化算法對優化問題進行求解,從而將求解時間縮短為原來的1%左右[10]。

在保證制冷機組穩定運行的前提下,進一步提高制冷機組運行效率是減小冷水機組整體能耗的有效途徑。蒸發器過熱度是表征制冷機組運行效率與穩定性的重要參數,設定較低的過熱度可以增加蒸發器的有效換熱面積,提高制冷機組運行效率,但根據最小穩定過熱度(MSS)理論[11],當蒸發器過熱度過低時,系統參數會出現嚴重振蕩。目前,大部分研究未充分考慮蒸發器過熱度對系統的影響,導致無法保證系統穩定性或者不能充分挖掘制冷機組的節能潛力。

本文通過建立壓縮式冷水機組系統穩態機理模型,以機組總能耗最小為優化目標,基于最小穩定過熱度理論[11],提出了一種改進過熱度約束條件,根據系統負荷取對應負荷下MSS值為過熱度約束下限,并采用遺傳算法求解系統設定值。實驗結果表明,本文提出的優化方法可以有效擴大尋優范圍,在保證系統穩定運行的同時進一步提高機組運行效率。

1 冷水機組穩態模型

壓縮式冷水機組主要包含3個子系統,即冷凍水系統、制冷機組系統和冷卻水系統,如圖1所示。

圖1 壓縮式冷水機組結構示意圖

水循環系統的主要動力來自冷凍水泵與冷卻水泵,水泵通過消耗電能來維持水介質循環流動,實現與制冷劑的換熱。制冷機組是冷水機組的核心部分,主要由壓縮機、冷凝器、節流閥及蒸發器4部件組成,其基本工作原理可以通過圖2所示的制冷循環壓焓(p-h)圖表示。

圖2中:o點為臨界點;ob為飽和液體線,其左側為過冷區;oc為飽和蒸汽線,其右側為過熱區;ob與oc之間的區域稱為兩相區。液態制冷劑在蒸發器內不斷從冷凍水吸熱蒸發為氣態,制冷劑溫度保持恒定(5—6),氣態制冷劑進入過熱區繼續吸熱升溫(6—1),1點與6點的溫度差即為蒸發器出口的過熱度。壓縮機消耗電能對氣態制冷劑做功,將制冷劑壓力由蒸發壓力pe升高到冷凝壓力pc(1—2);氣態制冷劑在冷凝器內向冷卻水放熱將蒸汽冷卻為液態(2—4);液態制冷劑經節流閥節流,壓力重新降為蒸發壓力(4—5)。

圖2 壓縮式制冷機組循環壓-焓圖

為實現冷水機組整體優化,首先需要根據制冷循環建立系統的穩態模型,以便在優化計算過程中確定系統變量。建模過程中出現的制冷劑溫度、焓值及密度等物性參數均通過美國國家標準計量局(NIST)開發的REFPROP軟件[12]查詢。

1.1 蒸發器模型

根據上述對制冷循環過程的分析,可將蒸發器內部按制冷劑狀態分為兩相區與過熱區兩部分,如圖3所示。

圖3 蒸發器相區原理圖

本文采用實際工程中應用比較廣泛的對數平均溫差(LMTD)法計算制冷劑側與水側溫差,并取LMTD校正因數為1,則蒸發器的穩態傳熱方程可以表示為

(1)

(2)

其中,Ue,sp與Se,sp分別為蒸發器過熱區傳熱系數與傳熱面積,Ue,tp為兩相區傳熱系數。由于Ue,sp與Ue,tp可以分別由制冷劑側與水側傳熱系數直接求出,因此式(2)中未知量僅為Se,sp,而Se,sp可以通過過熱區內制冷劑側與水側能量平衡方程求得

(3)

式中:Tchw,avg為冷凍水平均溫度。

過熱區與兩相區制冷劑側傳熱系數由Nusselt’s theory關聯式[13]表示

(4)

(5)

冷凍水側傳熱系數均由Shah關聯式[11]表示

(6)

式中:參數B通過冷卻水平均溫度計算

B=1 496+22Tw,avg

(7)

蒸發器模型另一個獨立方程為制冷劑側與冷凍水側能量平衡方程

(8)

1.2 壓縮機模型

壓縮機質量流量可以表示為[14]

(9)

式中:f、Vcom及ρi分別為壓縮機頻率、理論輸氣量和入口制冷劑密度;ηvol為壓縮機體積效率,根據下式計算

ηvol=0.98-0.085[(pc/pe)1/1.18-1]

(10)

另一方面,壓縮機對制冷劑做功可表示為[14]

Qcom=

(11)

式中:ccom,q,1、ccom,q,2為與壓縮機特性有關的常數,通過實驗辨識得到。因此,壓縮機能量守恒方程為

(12)

1.3 冷凝器模型

根據制冷機組整體能量守恒方程,冷凝器釋放熱量可以表示為

Qc=Qe+Qcom

(13)

與蒸發器類似,冷凝器內制冷劑側與冷卻水側的整體熱平衡方程可表示為

(14)

式中:Tclw,i為冷卻水入口溫度;Tclw,o為冷卻水出口溫度。

冷凝器過熱區與兩相區是其進行熱交換的主要區域,為簡化建模及求解過程,冷凝器模型只考慮兩相區與過熱區,忽略過冷區的影響。因此,根據冷凝器制冷劑側與冷卻水側的穩態傳熱方程,可得到冷凝器模型的另一個獨立方程

(15)

式中:Sc與Uc分別為冷凝器整體傳熱面積及換熱系數,Uc可表示為過熱區與兩相區整體傳熱系數的平均值

(16)

與蒸發器類似,冷凝器過熱區傳熱面積Sc,sp可以通過過熱區內制冷劑側與水側能量平衡方程求得

(17)

過熱區與兩相區制冷劑側傳熱系數分別由式(4)～式(7)計算。

1.4 過熱度模型

在確定系統主要運行參數后,通過蒸發壓力pe及蒸發器出口焓h1即可計算蒸發器出口過熱度。蒸發器過熱度為蒸發器出口溫度與飽和溫度之差

Tsh=T1(pe,h1)-Te(pe)

(18)

式中:Tsh為過熱度;Te為制冷劑蒸發壓力下飽和溫度;T1為蒸發器出口過熱蒸汽溫度,為蒸發壓力與出口焓值的函數。

式(1)、式(8)、式(12)～式(15)和式(18)構成冷水機組穩態模型,模型輸入輸出狀態如圖4所示。在冷水機組控制中,通常將蒸發壓力、過熱度及冷凝壓力作為被控變量,其中過熱度可由蒸發壓力及蒸發器出口焓值計算,若機組制冷量以及外部輸入已知,即可通過機組模型確定系統運行狀態。為簡化求解過程,本文選擇制冷機組內部參數蒸發壓力pe、冷凝壓力pc及壓縮機頻率fcom作為優化自由變量。

圖4 冷水機組模型結構

2 優化問題及求解

冷水機組耗能部件主要是壓縮機、冷凍水泵及冷卻水泵,降低機組能耗直接體現為3部分功耗之和最小,故優化目標函數可表示為如下形式

minWtotal=Wcom+Wchw+Wclw

(19)

式中:Wcom為冷水機組總功率;Wcom、Wchw及Wclw分別為壓縮機、冷凍水泵及冷卻水泵功耗。

2.1 壓縮機及水泵功耗模型

壓縮機功耗為理論功耗與功率系數之比

(20)

其中功率系數為

ηcom,p=ccom,η,1+ccom,η,2(pc/pe)ccom,η,3

(21)

式中:ccom,η,1、ccom,η,2、ccom,η,3為與壓縮機特性有關的常數。

冷凍水泵功耗可表示為冷凍水質量流量的多項式形式

(22)

與冷凍水泵類似,冷卻水泵功耗與冷卻水質量流量的關系如下

(23)

式(22)、式(23)中參數分別由實際數據擬合得到。

2.2 約束條件

冷水機組優化問題中的約束條件可分為自由變量約束、中間變量約束及過熱度約束,其中自由變量約束可表示為

(24)

中間變量約束為

(25)

較低的過熱度設定值可有效提高制冷機組的運行效率,這導致了過熱度優化值通常較低。然而由于MSS的存在,現有優化方法中過熱度約束相對比較保守,過熱度約束下限通常會高于最大熱負荷對應的MSS值。考慮到MSS隨熱負荷的下降而降低,本文將當前負荷對應的MSS取為過熱度約束下限,并隨工作條件變化動態改變。這樣,更富彈性的過熱度約束可以有效增大尋優空間,在進一步挖掘制冷機組節能潛力的同時保證系統的穩定運行。因此,最小化過熱度約束如下式所示

TMSS≤Tsh≤20

(26)

式中:TMSS為對應熱負荷下MSS值。

2.3 MSS曲線的實驗獲取

為了在提高系統運行效率的同時保證系統穩定,需要通過實驗獲得制冷機組在不同制冷量下的MSS值,具體步驟如下。

(1)在每一壓縮機頻率下給定一個較高的過熱度初始設定值,待系統穩定后檢測冷凍水流量、供回水溫差,計算系統穩態制冷量。

(2)逐漸減小過熱度設定值,如圖5所示,可以看到,隨著過熱度設定值的不斷降低,過熱度在調節過程中的波動幅度會逐漸增大。當設定值減小到某一臨界值后,過熱度會出現等幅振蕩,此臨界過熱度設定值加0.1 ℃即為該制冷量下系統的MSS值。

(3)逐漸降低壓縮機頻率(由50 Hz下降到30 Hz),并重復步驟(1)、(2)即可得到不同制冷量下的MSS值。

(4)根據上述實驗所得到的數據,利用Matlab工具箱將MSS值與對應制冷量進行多項式擬合,擬合值與實驗值對比見圖6,擬合公式如下

(27)

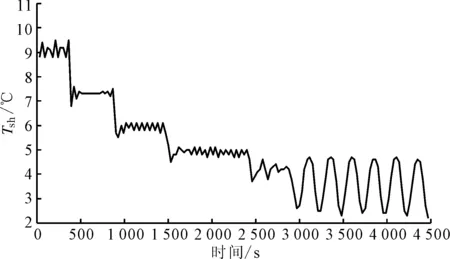
圖5 制冷量22 kW時MSS的獲取過程

圖6 不同制冷量下MSS擬合值及實驗值對比

2.4 優化問題的求解

遺傳算法具有較強的全局搜索能力和求解動態復雜系統的能力,本文采用遺傳算法尋求不同工況下冷水機組的最優設定點,實現系統各部分功耗的最優分配。以最小化機組總功耗Wtotal為優化目標,設計適應度函數以保證優化結果在可行域內[8]。函數式如下

(28)

式中:Ktotal為懲罰函數。采用遺傳算法進行優化的具體流程如圖7所示。

圖7 采用遺傳算法進行優化的流程

3 結果與討論

為驗證本文所提出的改進過熱度約束對于降低系統能耗的作用,在不同工況條件下設計兩組對比實驗,一組將過熱度約束設為目前常見形式7 ℃～25 ℃,另一組采取本文提出的改進過熱度約束,就兩種過熱度約束實驗結果進行對比。

實驗裝置為圖2所示的壓縮式冷水機組,通過可編程電加熱器模擬實際負荷變化,實驗裝置詳細描述見文獻[15]。實驗過程中,通過壓縮機-蒸發壓力、電子膨脹閥-過熱度以及冷卻水泵-冷凝壓力控制回路,將上述3個優化變量保持在優化設定值,以上3個控制回路均采用PI控制算法。冷水機組整體運行效率由所需制冷量與系統整體功耗之比(綜合制冷性能系數)表征

(29)

式中:SCOP機組綜合制冷性能系數。

3.1 變負荷工況對比實驗

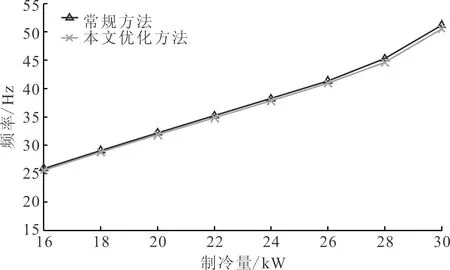
在變負荷工況對比實驗過程中,環境溫度為27.5 ℃,冷卻水回水溫度23.4 ℃,熱負荷由16 kW逐漸上升到30 kW,綜合制冷性能系數及過熱度對比結果如圖8與圖9所示。

圖8 兩種優化方法下綜合制冷性能系數對比結果

圖9 兩種優化方法下過熱度對比結果

由圖8可見,隨著制冷量的升高,系統綜合制冷性能系數逐漸降低。采用本文提出的改進過熱度優化方法,系統的綜合制冷性能系數由3.01逐漸下降到2.43,但在整個制冷量變化過程中均高于現有的優化方法。在熱負荷為22 kW時優化幅度最大,約為1.89%;在熱負荷為26 kW時最小,仍約為1.05%。

由于較低的過熱度可有效降低壓縮機運行功耗,因此兩種方法的過熱度優化值基本達到過熱度約束下界。由圖9可以看到,現有優化方法過熱度優化值均為7 ℃,本文方法的過熱度優化值隨著制冷量的降低逐漸減小,而且基本沿著MSS線變化(個別工作點略高于對應的MSS)。因此,在熱負荷較低的工況下,尋優范圍較大,節能效果較為明顯;隨著熱負荷增大,特別是大于26 kW后,兩種方法的過熱度優化值差距減小,節能效果也更為接近。

圖10給出了兩種優化方法下蒸發壓力、冷凝壓力及壓縮機頻率的優化結果;圖11比較了兩種優化方法下壓縮機及水泵功耗。從圖10a、圖10b可以看到,在部分負荷下,本文優化方法比現有優化方法得到的冷凝壓力優化值更低,蒸發壓力值更高。這是由于在最小過熱度約束條件下,過熱度尋優范圍擴大的結果,例如假設系統已經工作在現有優化方法得到的設定點,過熱度為7 ℃,若要在保證制冷量不變的條件下進一步降低過熱以提升系統能效,則需要增加膨脹閥開度并減小壓縮機頻率,從而使冷凝壓力下降,蒸發壓力上升。這樣,在壓縮機頻率及壓縮比同時減小的共同作用下,壓縮機的功耗得以進一步降低,如圖11a所示。

(a)蒸發壓力

(b)冷凝壓力

(c)壓縮機頻率圖10 兩種優化方法下系統運行工作點對比

(a)壓縮機功耗

由于主要通過優化制冷機組內部運行參數提升冷水機組運行效率,因此并不需要犧牲水泵功耗。由圖11b也可以看到,在不同熱負荷工況下,兩種優化方法下水泵功耗較為接近,本文優化方法下水泵功耗甚至更低。綜上所述,本文優化方法在合理分配制冷機組及水循環系統功耗基礎上,進一步挖掘了制冷機組的節能潛力,提升了冷水機組的整體運行效率。

(b)水泵功耗圖11 兩種方法壓縮機及水泵功耗的對比

3.2 負荷與環境溫度變化工況對比實驗

為進一步檢驗本文優化方法的實際節能效果,在熱負荷與環境溫度均變化的工況下設計對比實驗。這里以天津某建筑實際數據為基礎,用電加熱器模擬實際熱負荷。圖12為該建筑一天24 h熱負荷的變化情況,圖13為天津夏季環境溫度變化的典型情況,可以看到,由于墻體隔離作用,實際熱負荷變化比環境溫度滯后約1 h,這是因為但是兩者的變化趨勢基本一致。這是因為當熱負荷與環境溫度較高時,壓縮機與水泵將更多的熱量由冷凍水輸送到高溫冷卻水需要做更多的功,在增加制冷成本的同時導致節能空間減小。

圖12 天津某建筑熱負荷曲線

圖13 天津夏季環境溫度典型曲線

圖14給出了兩種優化方法在一天內綜合制冷性能系數的對比結果,可以看到,在所有時間點,本文方法的系統運行效率均高于現有優化方法。在熱負荷及環境溫度相對較高的14:00～16:00時間段,兩種方法的綜合制冷性能系數較低且非常接近,而在制冷成本較低的其他時段,綜合制冷性能系數相對較高,且本文方法對綜合制冷性能系數的提升較為明顯。

圖14 綜合制冷性能系數對比結果

最后,為進一步說明在不同時間點改進過熱度約束所帶來的節能效果,圖15給出了工作時段8:00～20:00中,本文方法的系統整體功耗及節能效果。從中可以看到,與現有優化方法相比,本文優化方法在所有時間點均進一步降低了冷水機組整體功耗。在制冷成本較高的14:00～16:00時平均節能約0.85%,而在上午9:00可進一步減少系統整體功耗達3.2%,在工作時段的平均節能量為1.92%。

圖15 工作時段中本文方法的系統功耗及節能效果

4 結 論

本文根據熱力學定律建立了壓縮式冷水機組穩態機理模型。在考慮到蒸發器過熱度對系統運行效率及穩定性影響的基礎上,提出了改進過熱度優化方法。與現有優化方法進行了一系列對比實驗表明:①改進過熱度約束可以有效擴大尋優范圍,從而比現有優化方法進一步降低了系統整體功耗,引入MSS值為冷水機組的穩定運行提供了理論保證;②由于系統MSS值隨著負荷的降低而降低,因此本文方法在部分負荷下可取得更為明顯的節能效果;③在夏季典型工況下的工作時段,比現有優化方法實現平均節能1.92%。本文的研究結果對節約壓縮式冷水機組運行成本、增強運行穩定性具有一定的實際意義。

參考文獻:

[1] JIANG Y. Chinese building energy consumption situation and energy efficiency strategy [J]. New Architecture,2008(2): 4-7.

[2] 陳丹丹,晉欣橋,杜志敏,等. 多臺冷水機組聯合運行空調系統的負荷優化分配 [J]. 上海交通大學學報,2007,41(6): 974-977.

CHEN Dandan,JIN Xinqiao,DU Zhimin,et al. The optimal loading strategy of multiple chillers in HVAC systems [J]. Journal of Shanghai Jiaotong University,2007,41(6): 974-977.

[3] 閆秀英,孟慶龍,任慶昌,等. 聯合運行冷水機組負荷優化分配及仿真研究 [J]. 暖通空調,2007,37(11): 18-21.

YAN Xiuying,MENG Qinglong,REN Qingchang,et al. Optimal load sharing strategy for multiple-chiller systems and its simulation [J]. Journal of HV&AC,2007,37(11): 18-21.

[4] NAVARRO-ESBRIJ J,GINESTAR D,BELMAN J M,et al. Application of a lumped model for predicting energy performance of a variable-speed vapour compression system [J]. Applied Thermal Engineering,2010,30(4): 286-294.

[5] LIU C W,CHUAH Y K. A study on an optimal approach temperature control strategy of condensing water temperature for energy saving [J]. International Journal of Refrigeration,2011,34(3):816-823.

[6] MA Z J,WANG S W. Supervisory and optimal control of central chiller plants using simplified adaptive models and genetic algorithm [J]. Applied Energy,2011,88(1):198-211.

[7] 王亞昆,吳愛國,董娜. 吸收式制冷機組逆神經網絡設定優化 [J]. 西安交通大學學報,2018,52(1): 123-142.

WANG Yakun,WU Aiguo,DONG Na. A set point optimization method for absorption chiller based on inverse neural network [J]. Journal of Xi’an Jiaotong University,2018,52(1): 123-142.

[8] 閆唯嘉,任慶昌,閆秀英. 基于遺傳算法的冷水機組負荷分配與出水溫度的優化 [J]. 制冷與空調(北京),2011,11(2): 37-40.

YAN Weijia,REN Qingchang,YAN Xiuying. Load distribution of chillers and the optimum of its outlet water based on genetic algorithm [J]. Refrigeration and Air-Conditioning,2011,11(2): 37-40.

[9] ZHAO L,CAI W J,DING X D,et al. Model-based optimization for vapor compression refrigeration cycle [J]. Energy,2013,55(55): 392-402.

[10] ZHAO L,CAI W J,DING X D,et al. Decentralized optimization for vapor compression refrigeration cycle [J]. Applied Thermal Engineering,2013,51(1/2): 753-763.

[11] FALLAHSOHI H,CHANGENET C,PLACE S,et al. Predictive functional control of an expansion valve for minimizing the superheat of an evaporator [J]. International Journal of Refrigeration,2010,33(2): 409-418.

[12] LEMMON E W,HUBER M L,MCLINDEN M O. NIST standard reference database 23: reference fluid thermodynamic and transport properties (REFPROP): version 8.0 [EB/OL]. (2007-11-02) . http://users.ugent.be/～mvbelleg/literatuur%20SCHX%20-%20Stijn%20Daelman/ORCNext/Supercritical/Software %20EES/REFPROP8.pdf.

[13] SHANG Y J,WU A G,FANG X,et al. Dynamic simulation of electronic expansion valve controlled refrigeration system under different heat transfer conditions [J]. International Journal of Refrigeration,2016,72: 41-52.

[14] DING X D,JIA L,CAI W J,et al. A hybrid modeling for the real-time control and optimization of compressors [C]// 2009 4th IEEE Conference on Industrial Electronics and Applications. Piscataway,NJ,USA: IEEE,2009: 3256-3261.

[15] SHANG Y J,WU A G,FANG X. A study on the modeling of the minimal stable superheat for a variable speed refrigeration system [J]. International Journal of Refrigeration,2015,59: 182-189.