變壓器繞組振動傳遞特性仿真研究

劉石,楊毅,田豐,高慶水,張楚

(廣東電網有限責任公司電力科學研究院,510080,廣州)

電力變壓器作為電網中的核心設備,其安全穩定運行與電網的可靠性密切相關。國內外的運行檢修經驗和變壓器事故后的解體研究證明,變壓器繞組在短路電流沖擊下發生的機械故障是變壓器故障的重要原因之一[1-3],因此開展變壓器的繞組機械故障檢測對于維護電網的安全穩定運行具有極為重要的意義[4]。自20世紀80年代以來,研究人員針對變壓器繞組的機械故障檢測提出了一系列的方法[5-7],在這些方法中,基于變壓器油箱表面振動信號的診斷方法具有與被測物沒有電氣聯系、易于實現在線監測的特點得到了廣泛的關注[8-9]。

變壓器油箱表面振動主要來自于變壓器鐵心的磁致伸縮效應以及繞組在交變的漏磁場中受到周期作用力而產生的強迫振動[10]。因此,當變壓器繞組發生機械變形和穩定性變化時,變壓器繞組的機械狀態可以通過油箱表面的振動信號表現出來,為故障檢測提供依據。國內外對于變壓器繞組振動機理的研究主要集中在繞組振動計算以及測點布置的研究上。

王豐華等通過磁-機械耦合模型研究了繞組的非線性振動特性[11];王洪方等建立了變壓器繞組安匝平衡時的軸向振動等效單自由度分析數學模型,研究了繞組軸向振動動態特性,討論了軸向預緊力-絕緣墊塊性能等參數對于繞組軸向動態特性的影響[12];朱葉葉等研究了變壓器繞組和鐵心的振動特性,并提出繞組和鐵心的合成振動矢量可能小于其中一個振動矢量的幅值[13];Garcia B通過線性擬合的方法獲得了油箱表面繞組振動和鐵心振動的合成特性[14]。

在測點位置的研究中,劉洪濤等將油箱壁分為加強筋和瓦楞結構,并將油箱分割成了若干矩形單元,通過沖擊力錘方法研究了油箱的固有頻率[15];陳楷等以電壓和電流為變量,利用最小二乘法對箱體表面不同測點的衰減系數進行了識別,認為高壓套管一側適合進行振動監測[16];徐方等利用線性偏差度分析的方法對測點進行研究,認為變壓器底部和靠近底部的箱體側面更適合傳感器布置[17];張雪冰等從板殼結構振動的有限元功率流理論出發,提出了變壓器板殼結構的有限元功率流計算方法,研究了油箱上橫向振動和總振動的功率分布,為測點布置提供了參考[18]。

由上述研究可以看出,目前在變壓器的振動機理和測點位置的研究中已經取得了大量而有效的成果,但是對于繞組振動在油箱中的傳遞機理和特性還缺乏相應的研究,而這對于完善基于振動信號的繞組機械狀態檢測技術具有十分重要的意義。

本文通過研究變壓器繞組在軸向和徑向的振動機理和特點,結合經典的波動方程,建立了繞組振動在變壓器油箱中的傳遞模型,并利用多物理場耦合軟件,建立了10/0.4 kV單相變壓器的三維模型,實現了變壓器繞組電磁力、繞組振動、油沖波動壓力以及油箱表面振動響應的耦合求解,獲得了額定電流幅值下油箱表面各處的振動加速度,并與實驗結果進行了驗證對比。

1 變壓器繞組振動機理及傳遞特性

變壓器繞組線匝在漏磁場中受到交變作用的洛倫茲力會產生周期振動。由于繞組結構的特點,同一餅間或段間的繞組通常由多根線匝并繞而成,因此可以將線匝的周期性振動分為繞組線餅的軸向振動以及墊塊撐條間線匝的振動。

1.1 繞組軸向振動機理

變壓器繞組在軸向上的振動通常可以采用經典的質量-彈簧-阻尼模型進行描述[19],如圖1所示。在這個模型中,變壓器線餅被視為質量塊,金屬線和墊塊的剛度被視為彈簧,墊塊和變壓器油的阻尼作用采用集中的阻尼進行表示。

圖1 線餅軸向振動的動力學模型

對于上述模型進行動力學分析,可以獲得繞組軸向振動的動力學方程

(1)

式中:M為繞組線餅的質量矩陣;u為線餅位移矩陣;C為阻尼系數矩陣;K為剛度系數矩陣;F為洛倫茲力矩陣;g為重力加速度。

在通有交流電流i=imcos(ωt+φ0)的作用下,繞組各處所受的洛倫茲力為

(2)

式中:p為系數矩陣,與導線所處的位置有關;聯立式(1)、式(2),可以獲得繞組線餅穩態下的軸向振動加速度

(3)

由此可見,變壓器穩態運行下繞組振動加速度的幅值與負載電流的平方成正比,頻率為電流頻率的2倍。

1.2 繞組徑向振動機理

繞組線匝在周向上被墊塊分割,形成兩端由墊塊和撐條固定,中間懸空的線匝,因而在交變力的作用下同樣會產生周期性的振動。文獻[20]采用靜力學方法對線匝的軸向和徑向進行了分析,指出在繞組軸向方向的線匝受力模型可以視為端部固定的均勻負載的梁,并給出了相應的計算公式與方法。應當注意的是,該理論來自于對導線在短路沖擊電流下的強度校核,在正常的穩態運行中,電流僅為短路時電流的10%左右,產生的洛倫茲力更是遠遠小于短路時的電磁力。因此,假設線匝在幅向上的振動滿足端部固定約束的歐拉-伯努利梁模型,可以獲得線匝的振動方程[21]為

(4)

式中:E為材料的彈性模量;I為線匝截面的慣性矩;y(x,t)為線匝的位移;ρl為材料密度;f(x,t)為線匝上的洛倫茲力。

由于繞組線匝的剛度大、質量小,使得線匝幅向振動的固有頻率遠高于激勵頻率,因此可以求取線匝在靜載荷下的撓度,從而獲得繞組的幅向振動位移及速度。

1.3 繞組振動在油中的傳遞機理

當變壓器繞組在交變的洛倫茲力作用下不斷產生軸向和徑向振動時,振動的線匝與變壓器油相互作用,使得油中的質點在平衡位置附近振動,并以機械波的形式由遠及近傳遞,傳遞規律需要滿足牛頓第二定理,質量守恒定理,描述壓強、溫度、體積的物態方程以及如下理想假設[22]。

(1)變壓器油為理想的流體煤質,不存在黏滯性,即振動波在傳遞過程中沒有能量損耗,同時只能以縱波的形式進行傳遞。

(2)沒有振動擾動時,變壓器油在宏觀上是均勻而靜止的,各質點的初速度為0,靜態壓強P0和靜態密度ρ0都是常數。

(3)振動的傳遞是絕熱的,不會因為傳遞過程引起的溫度差而產生熱交換,即忽略由于振動傳遞而引起的溫差。

(4)油中傳遞的是小振幅的振動波,各參量都是一階微量,動壓p遠遠小于靜態壓強p0,即p?p0;質點速度v遠遠小于機械波的波速c0,即v?c0;質點位移ζ遠遠小于波長λ,即ζ?λ;煤質的密度增量Δρ遠遠小于靜態密度ρ0,即Δρ?p0。

根據以上假設,可以得到變壓器油中的壓力p的波動方程

(5)

式中:c0為機械波在油中的傳遞速度;t為時間變量;2為拉普拉斯算子符,在直角坐標中的形式為

將式(5)分離為時間和空間變量后再進行傅里葉變換,可獲得頻域下振動在油中傳遞的Helmholtz波動方程[23]

(6)

式中:ω為圓周角頻率。

根據連續煤質的特點,在變壓器油和固體接觸的表面需滿足

(7)

式中:n為結構表面的外法向向量;utt為結構的加速度;ρ為變壓油密度。

2 繞組振動傳遞特性仿真研究

利用有限元軟件,對實驗室中的單相雙繞組變壓器進行仿真建模,實現電磁-結構-流體的耦合分析。忽略到變壓器繞組結構在交流磁場中集膚效應及勵磁電流,對變壓器內部磁場、洛倫茲力分布采用靜磁場計算。通過計算磁場中繞組的力密度,并與結構力學模塊進行單向耦合,實現模型計算數據的精確傳遞,避免了添加集中力而造成的求解結果不精確和采用多個有限元軟件而造成的計算流程繁瑣、數據和模型復雜,提高了計算的精度和準確度。同時,在繞組結構-變壓器油流體-箱體結構的分析中采用雙向耦合,充分考慮了2種類型和3個物理場之間的相互作用,提高了計算精度,計算流程如圖2所示。

圖2 電磁-結構-流體的耦合計算流程

2.1 模型參數及網格剖分

實驗變壓器為單相雙柱式結構,如圖3所示,具體參數如表1所示。

根據結構的對稱性,沿平行于鐵心的軋制方向對模型進行切割,形成1/2模型,并保留1個鐵心柱上的高低壓繞組,同時忽略油箱表面的套管及加強筋的影響,將其定義為薄殼結構,外殼厚度為3 mm,如圖4a所示。對整個求解區域采用四面體網格剖分,共獲得367 321個單元,模型網格如圖4b所示。

圖3 單相雙繞組變壓器結構

表1 單相變壓器參數

(a)1/2模型 (b)網格剖分結果圖4 1/2模型及網格剖分結果

2.2 變壓器繞組振動特性

根據交流電流下的洛倫茲力關系及式(2)可知,作用在繞組上的電磁力可分為幅值相等的恒定分量和正弦交變分量,因此結構分析中體積力密度為電磁分析結果中洛侖茲力密度的為1/2。利用磁場計算的洛倫茲力密度直接與繞組結構進行耦合,采用諧響應分析,獲得的低壓繞組的軸向和徑向振動加速度如圖5所示。由圖5可見:在軸向上,繞組的振動沿繞組的中心面對稱,上半部分的繞組與下半部分繞組的振動方向相反,使得整體繞組呈現出被壓縮的特點;繞組振動加速度最大值位于整個繞組的約1/4位置,幅值大約為0.08 mm/s2,由于鐵心窗的影響,繞組鐵心窗內的振動略小于繞組同一高度其他部位[24];徑向振動加速度主要來自于墊塊間的線匝振動,最大值約為0.25 mm/s2,同時徑向振動主要集中在繞組中部的線匝中,繞組端部的振動較弱。

(a)軸向振動加速度 (b)徑向振動加速度圖5 低壓繞組振動加速度

高壓繞組的軸向及徑向振動加速度如圖6所示。由圖6可見:軸向振動以繞組對稱面對稱,使得繞組整體呈現被壓縮的狀態,振動加速度的最大值集中在繞組端部墊塊的線匝之中,幅值約為0.1 mm/s2;繞組端部的徑向洛倫茲力分布不均勻,使得靠近端部的線匝產生了扭轉,該扭轉振動可徑向分解,因此增大了該區域的徑向振動,振動方向為沿繞組徑向外側。

(a)軸向振動加速度 (b)徑向振動加速度圖6 高壓繞組振動加速度

2.3 振動在油中的傳遞特性

利用有限元方法可以在分析中分別對高低壓繞組進行約束,進而對兩個繞組振動引起的油中壓力分布進行單獨研究。低壓繞組振動引起的油中壓力分布等值面如圖7所示,引起的油中最大壓力為74.59 mPa,位于繞組中部。由于徑向的振動,在兩個繞組之間形成了壓力較高的區域,由于軸向振動加速度的幅值位于繞組的約1/4位置,該位置附近的振動加速度相差不大,因而對油的壓力作用不明顯,而端部的加速度幅值較小,因而使得端部附近的油壓也較小。

圖7 低壓繞組振動引起的油中壓力等值面

高壓繞組引起的油中壓力分布的等值面如圖8所示。由圖8可見,壓力的最大值位于高壓繞組和端部的壓板之間,約為0.4 Pa,這是由于高壓繞組端部軸向振動的加速度較大,而端部壓板的加速度為0,使得端部和壓板之間的變壓器油受到擠壓,因而壓力升高。在油箱的側壁也形成了與圖7相似的壓力分布區域。

圖8 高壓繞組振動引起的油中壓力等值面

考慮高低壓繞組同時振動時油箱中的壓力分布的等值面如圖9所示。對比圖7和圖9可以看出,圖8和圖9的相似程度較高,分布范圍分別在-0.2～0.39 Pa和-0.15～0.39 Pa之間,說明兩個繞組同時振動產生的壓力主要取決于高壓繞組的振動。這是由于低壓繞組位于內側,振動產生的壓力在傳遞過程中容易受到外側繞組的阻擋,并且壓力隨傳播距離增大而衰減,因而不容易像外側傳遞,而高壓繞組位于外側且振源的面積較大,因此引起的油壓變化也較為明顯。比較圖7～圖9中油箱內側的壓力區域,說明油中的壓力分布滿足線性疊加定理,與假設一致。

圖9 高低壓繞組振動引起的油中壓力等值面

油壓傳遞到箱體引起的振動如圖10所示。從圖10可以看出,油箱表面振動加速度的最大值大致集中在正對繞組并且與高壓繞組距離最近的區域。該區域由于受到軸向和徑向兩種振動引起的壓力波的作用,在振動的分布上呈現出了沿繞組軸向對稱面上下對稱的特點,振動的最大幅值約為1.1 mm/s2。在靠近另一繞組的位置也出現振動較大的區域,這主要是由于振動的傳遞以及其在箱體內的折反射。根據線性疊加定理,當兩個鐵心柱上的繞組同時振動時,在圖10中振動強烈的區域,振動會相互疊加,使得上述區域的振動更加強烈。若認為油箱結構的響應也滿足線性,兩個繞組振動產生的油壓將使油箱表面的振動加速度增加一倍。

圖10 外殼表面振動加速度仿真云圖

3 繞組振動傳遞特性實驗

為了驗證上述理論及仿真結果的正確性,通過龍門吊吊起變壓器上部蓋板,使得和鐵心繞組與油箱沒有固體連接,在負載條件下僅對通過變壓器油傳遞至油箱表面的振動進行實驗。利用德國Polytec GmbH公司制造的便攜式數字激光測振儀PDV-100對油箱表面的振動進行測量,該激光測振儀的工作頻帶為0～22 kHz,傳輸時延為1 ms,量程為20 mm/s,分辨率為0.1 μm/s(有效值),測試系統如圖11所示。將油箱的一個正面劃分了63個測點,測點如圖12所示。

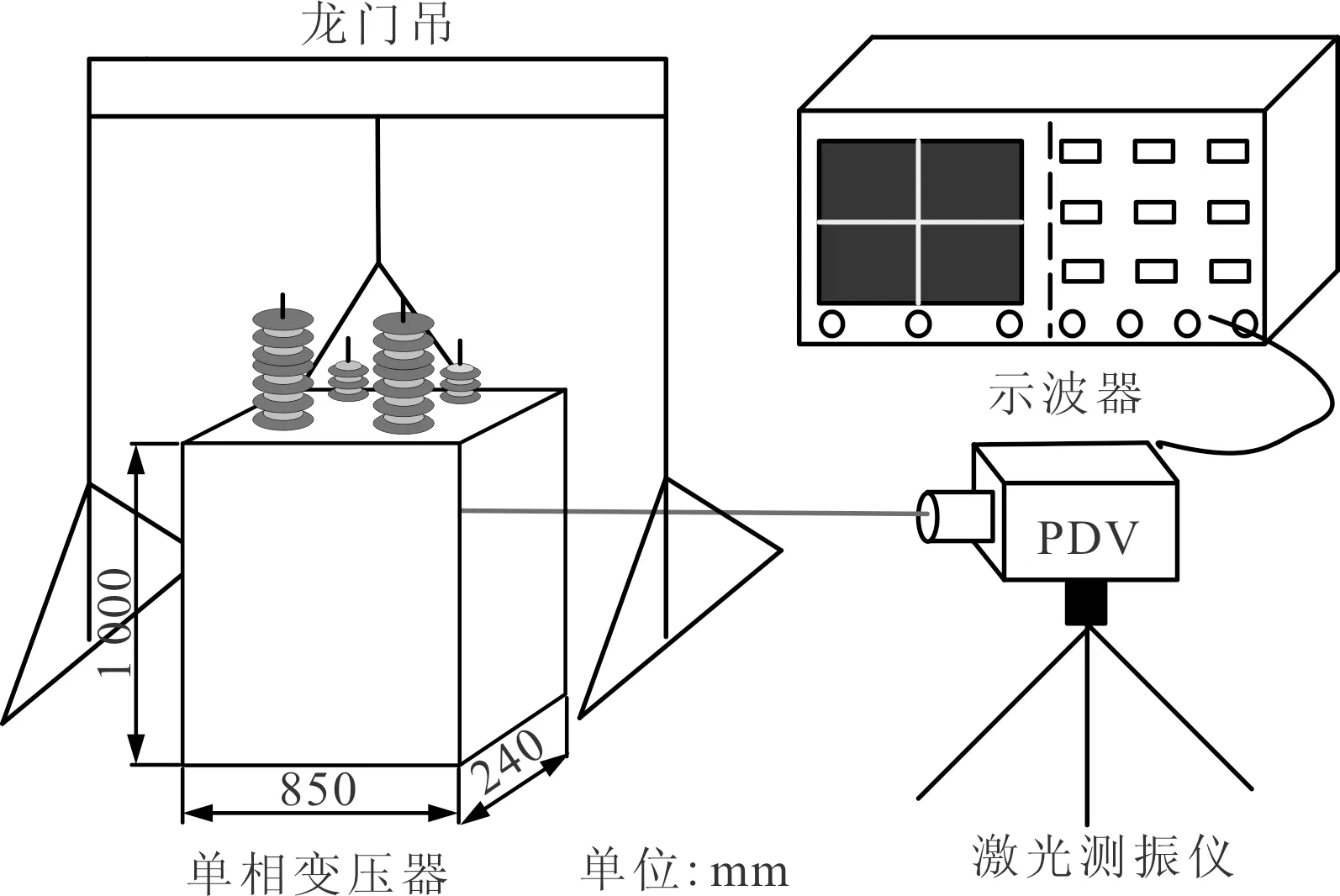
圖11 變壓器油箱表面振動測試系統示意圖

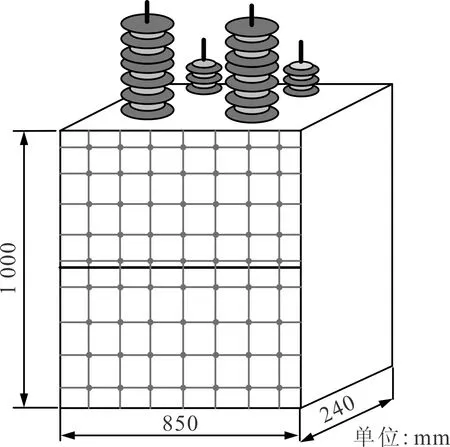
圖12 變壓器油箱一個表面測點分布示意圖

油箱表面振動如圖13所示。由實驗結果可得,變壓器振動的最大幅值約為3.6 mm/s2,位于油箱正面的左下角,而在此最大振動區域的附近,存在一個振動相位相反的區域,幅值約為-3.6 mm/s2。從整體振動的上下分布特點來看,實測和仿真的結果都表明下部的振動要略強于上部的振動。但在仿真結果中,繞組上部出現了兩個振動強烈的區域,與實測結果不同,造成這個現象的原因是由于仿真模型采用了上部封閉的殼式,使得油中的波動無法通過油箱上部的空氣向外傳遞,因此增大了上部的振動。根據仿真結果及線性疊加假設,將兩個鐵心柱上的繞組振動產生的油壓進行疊加后的振動幅值將小于實測結果,這是由于兩個繞組的漏磁場會相互影響,使得實際繞組的振動略大于單一繞組在漏磁場中的振動。

圖13 外殼正面振動加速度實測結果

4 結 論

本文在傳統的變壓器繞組振動機理的基礎上,提出了油中振動的傳遞理論,建立了電磁-結構-流體耦合的有限元分析模型,并對一臺單相變壓器的振動進行了仿真和實驗分析,得到了以下結論。

(1)振動在油中的傳遞滿足小幅波動理論,忽略變壓器油的黏滯作用,即認為油為具有線彈性的理想流體,振動在油中只能以縱波的形式傳遞,油中的壓力滿足線性疊加定理。

(2)由于低壓繞組位于繞組內側,因此振動產生的油的波動會受到外側繞組的阻礙,因此引起油箱表面振動的壓力主要來自于高壓繞組振動。

(3)油箱表面振動不僅與繞組自身的振動產生的壓力輻射場的分布有關,還與油箱本體的振動特性相關。因此在選擇測點時,應當盡量選擇油箱表面離繞組較近的平板區域以獲得較大的振動響應。

本文利用有限元法對變壓器的繞組振動特性進行了初步的仿真研究,下一步將在三相變壓器中開展相關的實驗研究工作,補充完善振動傳遞理論。

參考文獻:

[1] 凌愍,古正香. 1990—1994年全國變壓器事故統計及分析 [J]. 電網技術,1996,20(9): 47-52.

LING Min,GU Zhengxiang. Nation-wide fault statistics and analysis of transformers from 1990 to 1994 [J]. Power System Technology,1996,20(9): 47-52.

[2] 王夢云. 2005年110 kV及以上變壓器事故統計分析 [J]. 供用電,2006,23(1): 1-4.

WANG Mengyun. Statistical analysis of 110 kV and higher voltage transformer accident in 2005 [J]. Power Supply,2006,23(1): 1-4.

[3] CIGRE Working Group 05. An international survey on failures in large power transformers in service [EB/OL]. [2017-10-20]. https://e-cigre.org/publication/ELT_088_1-an-international-survey-on-failures-in-large-power-transformers.

[4] WANG M,VANDERMAAR A J,SRIVASTAVA K D. Review of condition assessment of power transformers in service [J]. IEEE Electrical Insulation Magazine,2002,18(6): 12-25.

[5] 王鈺,徐大可,李彥明,等. 檢測變壓器繞組變形的低壓脈沖法測試系統研究 [J]. 高電壓技術,1998,24(3): 24-27.

WANG Yu,XU Dake,LI Yanming,et al. A study on instrumentation techniques in LVI method for detecting transformer winding deformation [J]. High Voltage Engineering,1998,24(3): 24-27.

[6] 孫翔,何文林,詹江楊,等. 電力變壓器繞組變形檢測與診斷技術的現狀與發展 [J]. 高電壓技術,2016,42(4): 1207-1220.

SUN Xiang,HE Wenlin,ZHAN Jiangyang,et al. Current status and development of test and diagnostic technique of transformer winding deformation [J]. High Voltage Engineering,2016,42(4): 1207-1220.

[7] 陳偉根,趙立志,彭尚怡,等. 激光拉曼光譜應用于變壓器油中溶解氣體分析 [J]. 中國電機工程學報,2014,34(15): 2485-2492.

CHEN Weigen,ZHAO Lizhi,PENG Shangyi,et al. Analysis of dissolved gas in transformer oil based on laser Raman spectroscopy [J]. Proceedings of the CSEE,2014,34(15): 2485-2492.

[8] 汲勝昌,李彥明,傅晨釗. 負載電流法在基于振動信號分析法監測變壓器鐵心狀況中的應用 [J]. 中國電機工程學報,2003,23(6): 154-158.

JI Shengchang,LI Yanming,FU Chengzhao. Application of on-load current method in monitoring the condition of transformer’s core based on the vibration analysis method [J]. Proceedings of the CSEE,2003,23(6): 154-158.

[9] 馬宏忠,弓杰偉,李凱,等. 基于ANSYS Workbench的變壓器繞組松動分析及判定方法 [J]. 高電壓技術,2016,42(1): 192-199.

MA Hongzhong,GONG Jiewei,LI Kai,et al. Analysis and determination method for transformer winding looseness based on ANSYS workbench [J]. High Voltage Engineering,2016,42(1): 192-199.

[10] GARCIA B,BURGOS J C,ALONSON A M. Transformer tank vibration modelling as a method of detecting winding deformations: part Ⅰ Theoretical foundation [J]. IEEE Transactions on Power Delivery,2006,21(1): 157-163.

[11] 王豐華,段若晨,耿超,等. 基于“磁-機械”耦合場理論的電力變壓器繞組振動特性研究 [J]. 中國電機工程學報,2016,36(9): 2555-2562.

WANG Fenghua,DUAN Ruochen,GENG Chao,et al. Research of vibration characteristics of power transformer winding based on magnetic-mechanical coupling field theory [J]. Proceedings of the CSEE,2016,36(9): 2555-2562.

[12] 王洪方,王乃慶,李同生. 短路條件下變壓器繞組軸向振動等效單自由度分析 [J]. 電工技術學報,2000,15(5): 39-41.

WANG Hongfang,WANG Naiqing,LI Tongsheng. Axial vibration equivalent one-degree analysis of power transformer winding under short-circuit [J]. Transactions of China Electrotechnical Society,2000,15(5): 39-41.

[13] 朱葉葉,汲勝昌,張凡,等. 電力變壓器振動產生機理及影響因素研究 [J]. 西安交通大學學報,2015,49(6): 115-125.

ZHU Yeye,JI Shengchang,ZHANG Fan,et al. Vibration mechanism and influence factors in power transformers [J]. Journal of Xi’an Jiaotong University,2015,49(6): 115-125.

[14] GARCIA B,BURGOS J C,ALONSON A M. Transformer tank vibration modelling as a method of detecting winding deformations: part Ⅱ Experimental verification [J]. IEEE Transactions on Power Delivery,2006,21(1): 164-169.

[15] 劉洪濤,馬宏忠,高鵬,等. 利用變壓器箱體振動模型確定故障閾值 [J]. 電力系統及其自動化學報,2012,24(6): 36-40.

LIU Hongtao,MA Hongzhong,GAO Peng,et al. Method of determining the threshold of transformer fault using transformer tank vibration model [J]. Proceedings of the CSU-EPSA,2012,24(6): 36-40.

[16] 陳楷,王春寧,劉洪濤,等. 基于振動的變壓器監測與分析中最優測點選擇 [J]. 電力系統及其自動化學報,2013,25(3): 56-60.

CHEN Kai,WANG Chunning,LIU Hongtao,et al. Optimal measuring point selection based on monitoring and analysis of transformer vibration [J]. Proceedings of the CSU-EPSA,2013,25(3): 56-60.

[17] 徐方,邵宇鷹,金之儉,等. 變壓器振動測點位置選擇試驗研究 [J]. 華東電力,2012,40(2): 274-277.

XU Fang,SHAO Yuying,JIN Zhijian,et al. Experimental study of measuring point selection for transformer vibration detection [J]. East China Electric Power,2012,40(2): 274-277.

[18] 張雪冰. 變壓器油箱振動功率流與繞組故障非電量監測方法研究 [D]. 上海: 上海交通大學,2009: 25-37.

[19] WATTS G B. A mathematical treatment of the dynamic behaviour of a power-transformer winding under axial short-circuit forces [J]. Proceedings of the Institution of Electrical Engineers,1963,110(3): 551-560.

[20] 瓦修京斯基 C B(蘇). 變壓器的理論與計算 [M]. 崔立君,杜恩田,譯. 北京: 機械工業出版社,1983: 386-417.

[21] 劉延柱,陳文良,陳立群. 振動力學 [M]. 北京: 高等教育出版社,2000: 130-132.

[22] 杜功煥,朱哲民,龔秀芬. 聲學基礎 [M]. 南京: 南京大學出版社,2001: 163-184.

[23] 胡靜竹,劉滌塵,廖清芬,等. 基于有限元法的變壓器電磁振動噪聲分析 [J]. 電工技術學報,2016,31(15): 81-88.

HU Jingzhu,LIU Dichen,LIAO Qingfen,et al. Analysis of transformer electromagnetic vibration noise based on finite element method [J]. Transactions of China Electrotechnical Society,2016,31(15): 81-88.

[24] HORI Y,OKUYAMA K. Axial vibration analysis of transformer windings under short circuit conditions [J]. IEEE Transactions on Power Apparatus & Systems,1980,99(2): 443-451.