多分量調幅-調頻信號的瞬時頻率 直接計算與畸變消除方法
賈林山,張慶,2
(1.西安交通大學機械工程學院,710049,西安; 2.西安交通大學現代設計及轉子軸承系統教育部重點實驗,710049,西安)
瞬時頻率是調幅-調頻(AM-FM)信號的重要調制參數,對于探究非平穩、非線性過程的信息表征機制具有重要意義[1]。然而,由于調頻造成的頻域復雜性,傳統的基于穩態頻譜分離的解調技術無法獲得準確的瞬時頻率,因此研究瞬時頻率的求解方法具有重要意義。目前,有許多瞬時頻率求解方法,包括應用于經驗AM-FM分解中的直接正交法(DQ)與歸一化Hilbert變換法(NHT)[1]、應用于Hilbert-Huang變換中的Hilbert變換法(HT)[2]、應用于LMD中的直接計算法[3]、Teager能量算子法[4]等,近年來,復域能量算子解調法[5]等一些新的瞬時頻率求解方法也相繼被提出。
基于LMD的直接計算法是一種性能良好的瞬時頻率計算方法,具有不會出現難以解釋的負頻率、無明顯的端點效應等優點[6],目前已經成功應用于腦電信號分析[3]、轉子碰磨故障診斷[5]、齒輪和軸承故障診斷[7]、顫振識別[8]等領域。但是該方法也存在一些問題,首先通過反余弦函數求解得到的瞬時相位不是單調的,為獲得正的瞬時頻率,需要將之展開為單調遞增的瞬時相位,該步驟較為復雜,使得直接計算法的運行效率較低;其次,直接計算法求得的瞬時頻率在對應于純調頻信號極值點附近位置總是不可避免地存在較大的計算誤差,在瞬時頻率曲線上表現為明顯的畸變[9]。
針對直接計算法進行相位展開而導致的低效率的問題,本文提出了一種快速直接計算法,不需要進行相位展開,運行效率更高。針對直接計算法求取的瞬時頻率存在的畸變問題,本文提出了一種畸變定位與消除算法,可以較好地識別出畸變的發生位置,然后將畸變位置處的瞬時頻率剔除,最后使用三次樣條插值補全被剔除的數據,得到無畸變的瞬時頻率。
1 快速直接計算法
局部均值分解(LMD)是由英國學者Jonathan S.Smith在2005年提出的一種針對多分量AM-FM信號的解調方法[3],能自適應地將一個復雜的多分量AM-FM信號分解為若干個乘積函數(PF)分量之和,其中每一個PF分量是一個包絡信號和一個純調頻信號的乘積[3],包絡信號就是該PF分量的瞬時幅值(IA),而PF分量的瞬時頻率(IF)可由純調頻信號求出,從而實現對多分量AM-FM信號的解調。
文獻[3]在介紹LMD方法的同時,引入了直接計算法來計算每一個PF分量的瞬時頻率。設LMD分解得到的某一PF分量由包絡函數a(t)和純調頻信號s(t)相乘得到,即
PF(t)=a(t)s(t)
(1)
則PF的純調頻信號s(t)可以寫為一個余弦函數的形式,即
s(t)=cosφ(t)
(2)
那么瞬時相位φ(t)可以寫為純調頻信號s(t)的反余弦,且瞬時頻率f(t)通過瞬時相位直接求出,即
(3)
反余弦函數是定義在區間[-1,1]上的單調遞減函數,而純調頻信號一般為非單調函數,則瞬時相位φ(t)就不再是單調函數,因此如果直接按照式(3)求解f(t),將會產生負頻率。為解決這一問題,文獻[6]推導出了將非單調的瞬時相位整體展開為單調遞增瞬時相位的基本步驟,文獻[3]提出將波形分段,在一個全波內將相位展開。這兩種方法都需要將相位展開,運行效率較低。
相位展開的實質就是將原本非單調的瞬時相位序列中的遞減部分序列變換為遞增序列,這一過程對于式(3)來講,由單調遞增的展開相位和非單調的未展開相位求得的瞬時頻率f(t)在負頻率部分恰好互為相反數,因此相位展開(無論是分段相位展開還是全局相位展開)并不是保證最終求得的瞬時頻率為正的必要條件。基于以上分析,本文提出一種快速直接計算法,具體步驟如下。
(1)設乘積函數PF的純調頻信號為s(t),為保證s(t)所有取值在反余弦函數定義域內,將s(t)的所有極大值點置為1,所有極小值點置為-1,然后將s(t)所有大于1的點置為1,所有小于-1的點置為-1,最終使s(t)滿足-1≤s(t)≤1。將調頻信號s(t)取反余弦,得到非單調的瞬時相位
φ(t)=arccoss(t)
(4)
(2)對非單調的瞬時相位φ(t)進行前向差分,設信號采樣頻率為fs,得到包含有負瞬時頻率的初始瞬時頻率
(5)
式中:diff表示后向差分運算。
(3)對初始瞬時頻率f0(t)取絕對值,得到全部為正值的瞬時頻率
f1(t)=|f0(t)|
(6)
通過相位展開獲得單調遞增的瞬時相位這一過程是為滿足瞬時頻率須由單調遞增的瞬時相位差分得到這一數學定義,但是從計算角度來說,相位展開與否并不影響求得的瞬時頻率的絕對值,因此可以免去不必要的相位展開計算,在不影響結果的前提下,獲得更高的計算效率。
需要說明的是,此時f1(t)中不可避免地存在大量畸變點,其原因是:將反余弦函數的導數代入式(3)中得到
(7)
當s(t)接近于1時,分母接近于0,使得s′(t)的誤差被放大[10],從而在極值點附近產生畸變。該畸變具有孤立出現、幅值大幅變化的毛刺狀特點,使求解出的瞬時頻率不可直接使用。
2 直接計算法畸變定位與消除算法
使用直接計算法得到的瞬時頻率在對應于純調頻信號極值點附近總是存在毛刺狀畸變點,必須要經過消除毛刺處理才能得到可用的瞬時頻率,通常采用中值濾波法[1]、滑動平均法[6]、形態學濾波法[11]等用于消除畸變。然而,上述方法存在3點問題:首先,對瞬時頻率畸變位置的出現規律缺乏深入探究;其次,采取的方法需要一定的先驗知識,比如,如何選擇滑動步長和平滑次數,如何選擇形態學濾波的結構元素形狀和長度等;第三,在處理瞬時頻率的畸變點時,不可避免地對非畸變點產生影響,即不具備局部處理特性。
為此,對畸變的出現位置進行分析,發現畸變均位于極值點附近,根據極值點處采樣點分布的不同,可以分為三角分布型和梯形分布型2大類。選取純調頻信號s(t)的極值點以及左右兩側各兩個采樣點構成一個5點區域,對區域內各點根據幅值進行降序排序,分別為D1~D5,則出現以下兩種情況:
(1)如果D3點幅值絕對值更靠近D2,則為三角分布型,若D3點在D2左側,則D1和D2是畸變點;若D3點在D2右側,則D1和D3是畸變點。
(2)如果D3點幅值絕對值更靠近D4,則為梯形分布型,若D3點在D2左側,則D1、D2和D4是畸變點;若D3點在D2右側,則D1、D2和D3是畸變點。
設計畸變定位與消除算法,具體步驟如下。
(1)設乘積函數PF的純調頻信號為s(t),為保證s(t)所有取值在反余弦函數定義域內,將s(t)的所有極大值點置為1,所有極小值點置為-1,并將s(t)中大于1的點置為1,小于-1的點置為-1,使s(t)滿足-1≤s(t)≤1。
(2)找出信號s(t)的第一個極值點E1,將s(t)的極值點位置及其兩側各2個采樣點位置共計5個點按幅值的絕對值大小進行降序排序,分別標識為D1~D5,其對應采樣時刻分別為tD1~tD5。
(3)設Z=|s(tD3)-s(tD2)|-|s(tD4)-s(tD3)|。那么如果Z<0,為三角分布型,若tD3 如果Z>0,為梯形分布型,那么若tD3 (4)處理完第1個極值點E1后,再對下一個極值點重復進行步驟(1)~(4),直至所有的極值點都被處理完成,輸出畸變位置序列T。 (5)將帶有毛刺的瞬時頻率f1(t)在毛刺位置序列T處的數據刪除,并使用三次樣條插補出毛刺位置序列T處的瞬時頻率值,最終可以得到無毛刺的瞬時頻率f(t)。 上述算法要求純調頻信號s(t)的每一個全波至少應有6個采樣點,因此本文提出的毛刺定位算法對采樣頻率具有適用性條件,即采樣頻率不得低于s(t)中最高瞬時頻率的6倍。同時,從上述算法畸變定位結果來看,在一般情況下,每一個極值點位置一般有2~3個畸變點,即高于1/6~1/4采樣頻率的瞬時頻率可能無法由直接反余弦法正確解出。 考察由兩個AM-FM分量組成的仿真信號 x(t)=(1+0.5cos(8πt))cos(200πt+ 2cos(10πt))+0.8sin(πt)sin(30πt), t∈[0,1] (8) 設定采樣頻率為1 024 Hz,其時域波形見圖1。 圖1 仿真信號x(t)的時域波形圖 為了提取兩個分量的瞬時頻率,首先需要采用LMD方法對x(t)進行分解,得到兩個PF分量和1個余項R,如圖2所示。從圖2中可以看出,x(t)中的兩個AM-FM分量分別對應前兩個PF分量。 為比較本文提出的快速直接計算法和傳統的基于相位展開的直接計算法[6]的運行效率,分別使用兩種方法求解PF1分量的純調頻信號s1(t)的瞬時頻率。在相同計算機環境下,連續運行5次,記錄運行時間如表1所示,最終取平均值得到二者平均運行時間之比為25.748 2。即針對本例,本文提出的快速直接計算法的運行效率大約是基于相位展開的直接計算法的25倍左右,速度優勢較為明顯。 圖2 仿真信號x(t)的LMD分解結果 表1 兩種方法運行時間的比較 基于相位展開的直接計算法得到s1(t)的瞬時頻率如圖3所示,本文提出的快速直接計算法得到s1(t)的瞬時頻率如圖4所示,二者波形一致。 圖3 基于相位展開的直接計算法得到的瞬時頻率 圖4 本文方法得到的瞬時頻率 從圖4中可見,直接計算法求得的瞬時頻率存在大量毛刺狀畸變點,為保證結果有效,需要把這些畸變點去除。按照第2節提出的畸變定位與消除算法對使用本文算法求得的存在畸變的瞬時頻率進行定位和消除。首先將所有的畸變點定位,使用“*”標識出了所有的畸變點位置,如圖5所示。然后,將畸變點位置數據剔除,使用三次樣條插值將畸變點位置數據補全,最終得到s1(t)的IF曲線如圖6所示。從圖6中可以看出,原本布滿毛刺的IF曲線中的畸變點被有效去除。 圖5 畸變點定位標識 圖6 去除畸變后的瞬時頻率 使用Hilbert變換對s1(t)求解瞬時頻率,即歸一化Hilbert變換[1],得到IF曲線如圖7所示。 圖7 使用歸一化Hilbert變換求取的s(t)的瞬時頻率 對比圖6和圖7,兩者形狀基本相近,均存在一定波動,也即由LMD對信號x(t)分解得到的PF1分量的純調頻信號中實際的瞬時頻率確實如圖6和圖7所示的那樣,存在不平滑的波動,這種波動是由于LMD分解過程中的誤差導致的,而不是由信號提取方式(NHT或直接計算法)導致的。 為更深入地說明該問題,使用滑動平均法[12]對帶有畸變點的瞬時頻率進行平滑,這里設定滑動步長為5,滑動平均次數為10,得到的結果如圖8所示。 圖8 使用滑動平均法處理畸變后的瞬時頻率 圖8與圖7相比看起來更加平滑和精確,但在平滑畸變點的過程中,LMD本身的分解誤差也被平滑而丟失了。本文方法是僅將畸變點去除,然后使用插值補全,未對非畸變位置數據進行修改,在選擇性剔除畸變點的同時,完整地保留了LMD自身分解誤差導致瞬時頻率波動,具有局部處理的特性,這是本方法與傳統的如滑動平均、形態學濾波、中值濾波等全局處理方法的一個重要的不同之處。此外,識別畸變點位置是全部無參數的,不依賴于使用者的經驗,這也是本文方法的重要優勢。 為進一步驗證本文方法的有效性,以某煙氣輪機碰磨故障的轉子位移信號為例進行分析。煙氣輪機工作轉速為446 r/min,工作頻率為7.43 Hz,信號采樣頻率為200 Hz,其信號波形如圖9所示。 圖9 煙氣輪機轉子碰磨信號時域波形 當發生碰磨故障時,轉子位移信號為多分量AM-FM信號,其中的每一個分量都是由工頻的倍頻為載頻,以工頻為調制頻率的具有物理意義的單分量AM-FM信號。從理論上來講,只要求出其中某一個單分量AM-FM信號的瞬時頻率,并對瞬時頻率作幅值譜,便可找到蘊藏在信號中的頻率調制信息,實現轉子碰磨的故障診斷。為此使用LMD將信號分解,得到3個PF分量和1個余項,如圖10所示。 圖10 轉子碰磨信號的LMD分解結果 使用本文方法對得到的PF分量求解瞬時頻率,發現PF2對應的瞬時頻率在二倍頻附近周期性波動,如圖11所示。為得到確切的調頻頻率,分析PF2對應的瞬時頻率的幅值譜,如圖12所示。從圖12可以看出,幅值譜主峰為工頻,即PF2中存在頻率調制,其調制頻率為工頻,即PF2瞬時頻率曲線中周期性波動的頻率為工頻,因此可以判斷煙氣輪機轉子發生了碰磨故障,與實際情況相符。 圖11 PF2純調頻信號的瞬時頻率 圖12 PF2純調頻信號的瞬時頻率的幅值譜 瞬時頻率在語音信號分析領域具有廣泛應用[13]。為進一步說明本文方法的適用性,以語音信號為例進行分析。 使用聲音傳感器在48 kHz采樣率下采集雙元音/ei/的聲音信號,發音者為男性,保存為wav格式,波形和頻譜如圖13所示。 (a)語音信號 (b)信號頻譜圖13 雙元音/ei/語音信號及信號頻譜 截取0.3~0.4 s的語音信號進行LMD分解,得到6個PF分量,其中前3個PF分量如圖14所示。 圖14 雙元音/ei/語音信號的LMD分解結果 經過分析發現,PF1分量主要為高頻噪聲,而PF2分量保留了原始信號中的大部分能量,從PF2分量波形可以看出符合元音具有周期性脈沖的特點,脈沖的間隔周期的倒數即為基音頻率。將PF2作為分析對象,使用本文方法分析其純調頻信號的瞬時頻率,如圖15所示。 圖15 PF2純調頻信號的瞬時頻率 圖16 PF2純調頻信號瞬時頻率的幅值譜 從圖15可以發現,PF2的瞬時頻率在第1個共振峰中心頻率f1附近波動,瞬時頻率的幅值譜如圖16所示。從圖16可以看出,頻譜中存在最高譜峰,對應頻率為基頻154 Hz,即PF2中信號瞬時頻率以154 Hz頻率波動,從而有效提取出該語音信號中的基音頻率。 本文研究了一種瞬時頻率快速直接計算方法,并針對該方法求得的瞬時頻率存在大量畸變點的問題,提出了一種無參數的畸變定位與消除算法,得到了如下結論。 (1)在保證和傳統的基于相位展開的瞬時頻率的直接計算法的結果一致的情況下,提出的瞬時頻率快速直接計算方法運行效率更高,算法更加簡單。 (2)與傳統的畸變消除方法相比,本文的畸變定位與消除算法具有無參數、局部處理的優勢。 (3)本文提出的瞬時頻率快速直接計算法和畸變與定位消除算法可以得到正的、有物理意義的瞬時頻率,并成功用于機械故障診斷與語音信號基音頻率識別。 參考文獻: [1] HUANG N E,WU Zhaohua,LONG S R,et al. On instantaneous frequency [J]. Advances in Adaptive Data Analysis,2009,1(2): 177-229. [2] HUANG N E,SHEN Z,LONG S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society: A Mathematical,Physical & Engineering Sciences,1998,454(1971): 903-995. [3] SMITH J S. The local mean decomposition and its application to EEG perception data [J]. Journal of the Royal Society Interface,2005,2(5): 443-454. [4] MARAGOS P,KAISER J F,QUATIERI T F. On amplitude and frequency demodulation using energy operators [J]. IEEE Transactions on Signal Processing,1993,41(4): 1532-1550. [5] ZENG M,YANG Y,ZHENG J. et al. Normalized complex Teager energy operator demodulation method and its application to fault diagnosis in a rubbing rotor system [J]. Mechanical Systems and Signal Processing,2015(50/51): 380-399. [6] 任達千,楊世錫,吳昭同,等. 信號瞬時頻率直接計算法與Hilbert變換及Teager能量法比較 [J]. 機械工程學報,2013,49(9): 42-48. REN Daqian,YANG Shixi,WU Zhaotong,et al. Comparison of instantaneous frequency directed computing method and Hilbert transform and Teager energy method [J]. Journal of Mechanical Engineering,2013,49(9): 42-48. [7] 張亢,程軍圣,楊宇,等. 基于分段波形的信號瞬時頻率計算方法 [J]. 湖南大學學報(自然科學版),2011,38(11): 54-59. ZHANG Kang,CHENG Junsheng,YANG Yu,et al. A piece-wise based signal instantaneous frequency computing method [J]. Journal of Hunan University (Natural Sciences),2011,38(11): 54-59. [8] SUN H,ZHANG X,WANG J. Online machining chatter forecast based on improved local mean decomposition [J]. International Journal of Advanced Manufacturing Technology,2016,84(5/6/7/8): 1045-1056. [9] 陳保家,何正嘉,陳雪峰,等. 機車故障診斷的局域均值分解解調方法 [J]. 西安交通大學學報,2010,44(5): 40-44. CHEN Baojia,HE Zhengjia,CHEN Xuefeng,et al. Locomotive fault diagnosis based on local mean decomposition demodulating approach [J]. Journal of Xi’an Jiaotong University,2010,44(5): 40-44. [10] 任達千. 基于局域均值分解的旋轉機械故障特征提取方法及系統研究 [D]. 杭州: 浙江大學,2008: 31-32. [11] 唐貴基,王曉龍. LMD的LabVIEW實現及其在齒輪故障診斷中的應用 [J]. 中國測試,2014,40(1): 101-105. TANG Guiji,WANG Xiaolong. LMD realization by LabVIEW and its application in gear fault diagnosis [J]. China Measurement & Test,2009,43(3): 523-528. [12] 任達千,楊世錫,吳昭同,等. 基于LMD的信號瞬時頻率求取方法及實驗 [J]. 浙江大學學報(工學版),2009,43(3): 523-528. REN Daqian,YANG Shixi,WU Zhaotong,et al. Instantaneous frequency extraction method and experiment based LMD [J]. Journal of Zhejiang University (Engineering Science),2009,43(3): 523-528. [13] SCHLOTTHAUER G,TORRES M E,RUFINER H L. A new algorithm for instantaneousF0,speech extraction based on ensemble empirical mode decomposition [C]//European Signal Processing Conference. Piscataway,NJ,USA IEEE,2015: 2347-2351.3 仿真信號分析



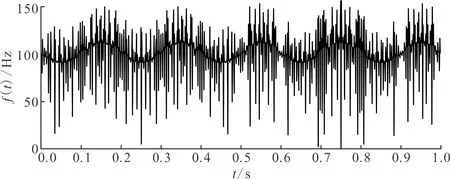





4 試驗信號分析
4.1 轉子碰磨故障診斷


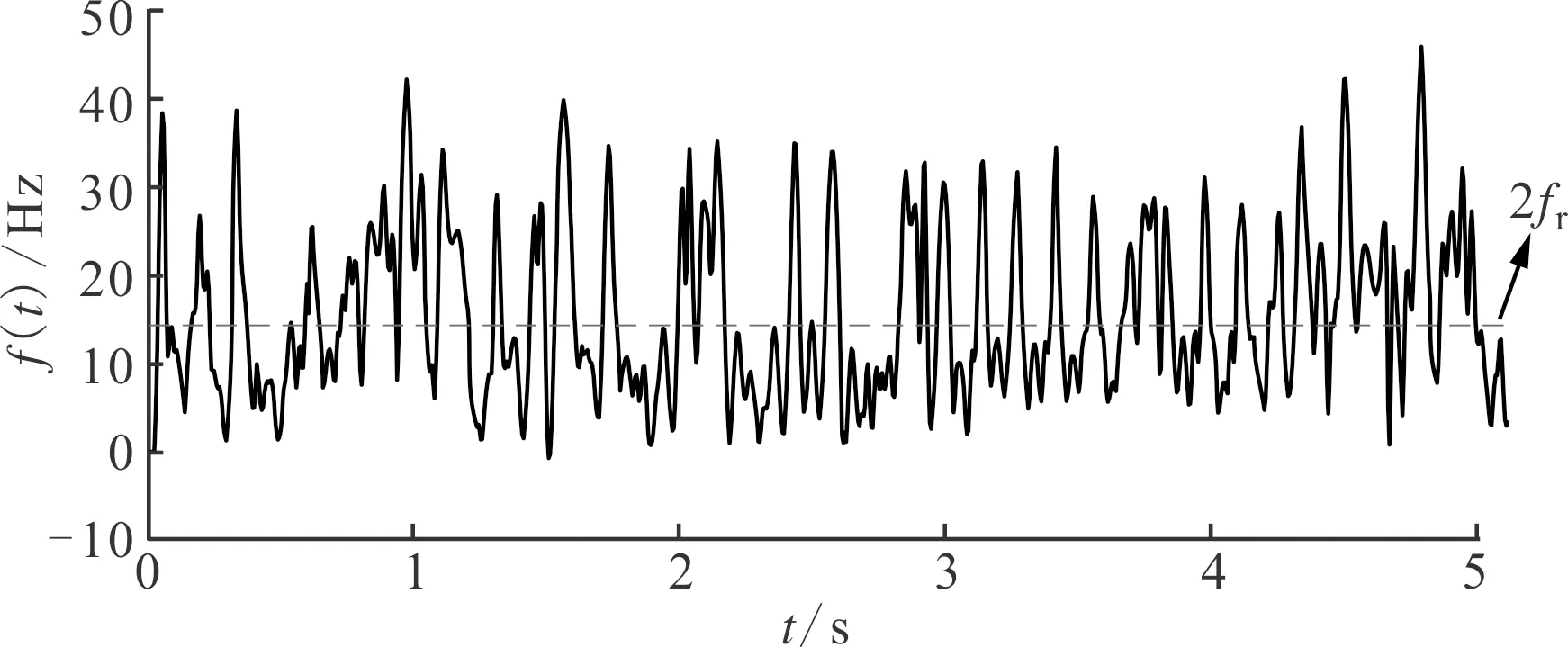

4.2 語音信號分析





5 結 論

