氣囊隔振器囊體簾線等效平衡纏繞角理論與試驗研究

金 著， 何 琳， 趙應龍(1． 海軍工程大學 振動與噪聲研究所， 武漢 430033; 2. 船舶振動噪聲重點實驗室, 武漢 430033)

氣囊隔振器是一種以壓縮氣體為彈性體，以壓縮氣體的反力作為彈性恢復力，低頻隔振性能優良的隔振器，在軌道交通和艦船減振降噪領域應用廣泛[1-4]。由橡膠芳綸復合材料制成的囊體是氣囊隔振器的主要構成部分，起到力學平衡和密封的作用，氣囊囊體復合材料的設計和制作對氣囊隔振器的性能具有決定性的影響[5-7]。氣囊隔振器囊體平衡性設計的主要對象是芳綸簾線增強層的纏繞角度，合適的芳綸纏繞角度能夠保證囊體在充氣狀態下的平衡性和氣囊使用的穩定性和耐久性[8]。目前，針對囊體芳綸簾線纏繞角度的理論研究已解決其理論平衡纏繞角的計算問題，但計算結果的可操作性差，無法指導氣囊隔振器的批量化生產，因此有學者提出了簾線等效平衡纏繞角的概念，使得簾線按該角度纏繞時，氣囊囊壁的性能能夠最為接近按照理論角度纏繞時的性能，從而達到簡化工藝的目的，為氣囊隔振器的量產化工作奠定基礎[9]。

本文根據氣囊隔振器囊體簾線等效平衡纏繞角度理論，通過理論分析，計算了囊體簾線纏繞的最優等效平衡纏繞角，并通過有限元仿真分析和試驗驗證了等效平衡纏繞角在氣囊承載特性和剛度特性上的等效性。

1 理 論

1.1 氣囊隔振器基本理論

氣囊隔振器基本理論主要是以氣囊有效承載面積為核心構建起的用于計算其承載特性、剛度、固有頻率等性能參數的理論。其中，氣囊隔振器的承載力計算公式為

F=PSe

(1)

式中:P為氣囊隔振器囊內氣壓;Se即為氣囊的有效承載面積。

氣囊隔振器剛度計算公式為

(2)

式中：V表示囊體容積；Pa表示大氣壓力；dz表示氣囊在承載方向的位移微元；n是氣體多變指數，其數值在1.0～1.4之間，計算氣囊靜剛度時取n=1，動剛度時取n=1.4。

氣囊隔振器固有頻率計算式為

(3)

式中：Kd0為氣囊動剛度；F0為固有頻率計算載荷狀態下的氣囊承載力。

1.2 等效平衡纏繞角理論

氣囊隔振器囊體簾線理論平衡纏繞角的計算原理圖如圖1所示，其計算公式如式(4)所示[10]

(4)

式中：R為氣囊回轉半徑，r是下側囊體波紋角回轉半徑。易見，簾線理論纏繞角α隨囊壁波紋角φ變化而變化，這導致在工藝上實現簾線的準確纏繞十分困難。因此，提出氣囊隔振器囊體簾線等效平衡纏繞角的概念，實現簾線纏繞角度恒定，氣囊性能不變的目的。

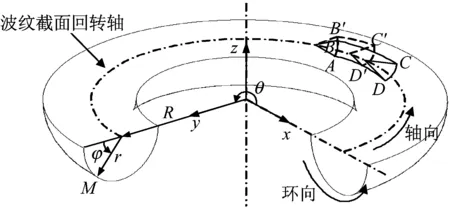
圖1 囊體結構及微元示意圖Fig.1 Capsule structure and its infinitesimal unit

由于簾線的纏繞角度對囊體平衡性的影響，按囊體結構可分為導致囊體環向變形和導致囊體軸向變形，因此，等效平衡纏繞角的計算也分為環向計算和軸向計算。由于芳綸簾線具有極高的強度，在氣囊正常承載情況下，簾線伸長率可忽略不計。

氣囊隔振器囊體在恒定簾線纏繞角下的環向和軸向變形的計算公式如式(5)，(6)所示

(5)

(6)

式中：α為簾線理論平衡纏繞角，其計算如式(4)所示；β為簾線的實際纏繞角，且不隨囊體波紋角φ變化而變化。

對于軸向伸長量，由于囊體軸向周長是變化的，因此Δln無法準確反應囊體變形量的相對大小。本文用波紋角φ處的囊壁變形后的半徑增量與原半徑的百分比η來描述囊體變形大小，如圖2所示。

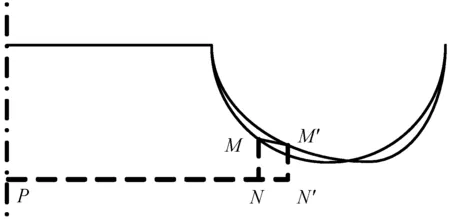
圖2 囊體半徑增量百分比示意圖Fig.2 Increasing percentage of the capsule’s radius

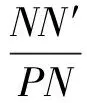
(7)

那么，找到合適的簾線纏繞角β，使得囊體的環向變形和軸向變形最小，且處于工程上可接受的范圍，即為等效平衡纏繞角。

1.3 算例分析

1.3.1 基本參數計算

本文研究對象為典型膜式氣囊隔振器(RSAS)結構，其囊體剖面結構如圖3所示，根據使用經驗，影響氣囊平衡性的主要是下半部分囊體，這部分囊體呈半圓形回轉體結構，其三維結構如圖1所示。

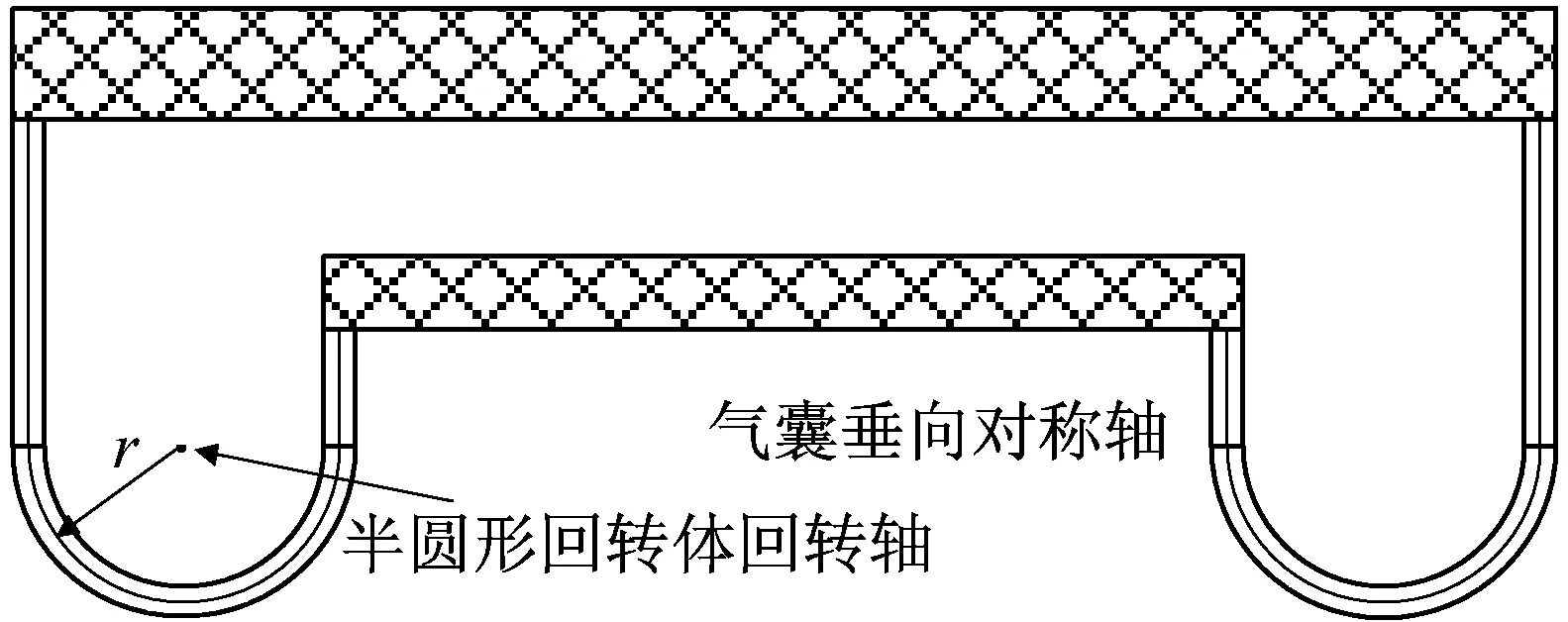
圖3 本文算例膜式氣囊隔振器結構簡圖Fig.3 Structure of the RSAS used in this paper

該膜式氣囊隔振器的主要形狀參數和變形參數如表1所示。

將表1中參數代入式(1) ～ (3)，計算得算例膜式氣囊隔振器的承載力為靜、動態剛度分別為

表1 算例膜式氣囊主要參數Tab.1 Main parameters of the RSAS

F=3.848×104N

k0=1.082 kN/mm

kd0=1.515 kN/mm

計算載荷下固有頻率為

f0=3.126 Hz

1.3.2 等效平衡纏繞角計算

將表1中參數代入式(4)，可得算例氣囊下側半圓形回轉部分簾線的平衡纏繞角度，如圖4所示。

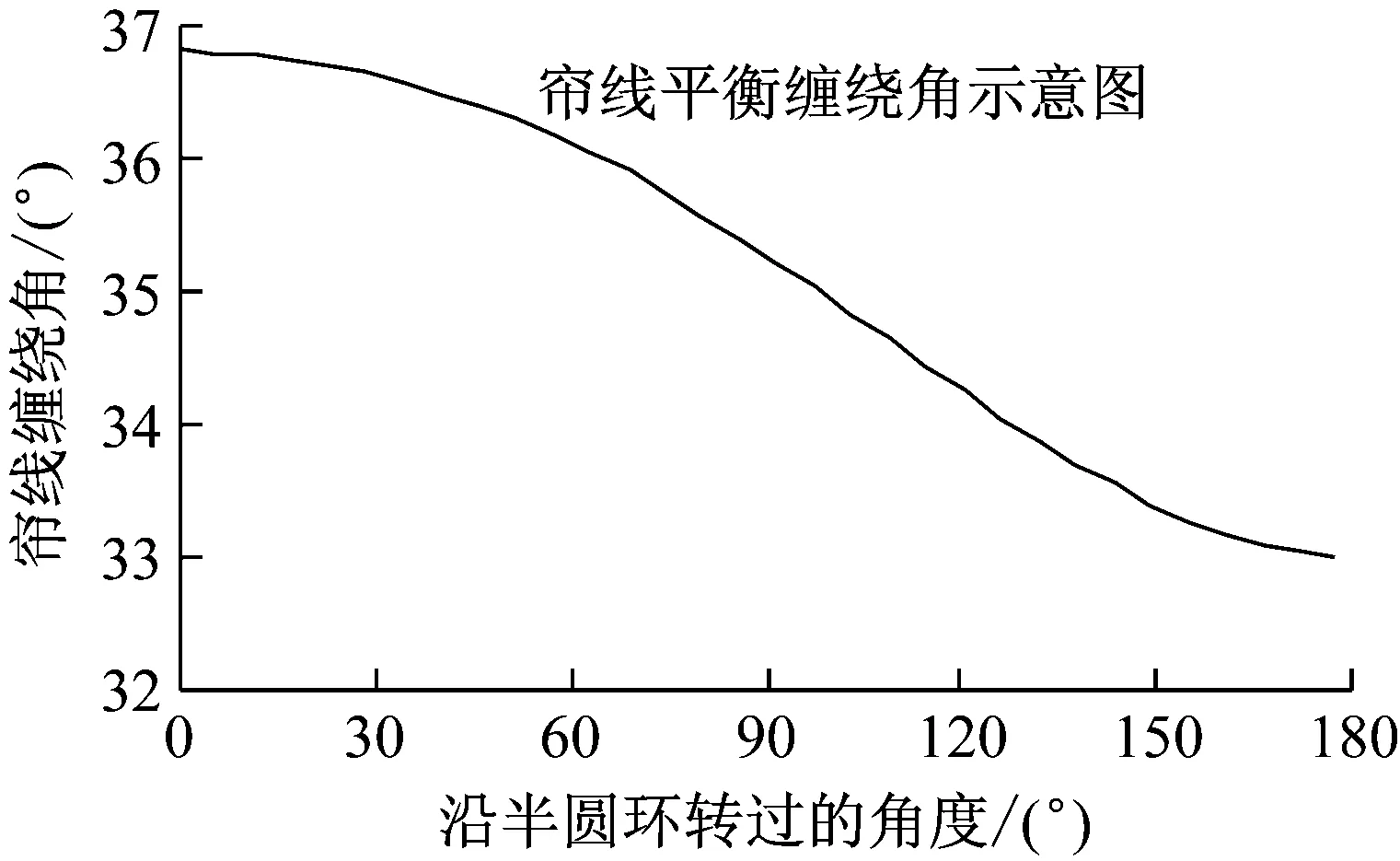
圖4 簾線理論平衡纏繞角Fig.4 Cord’s theoretical equilibrium-wind angle

可見簾線的平衡纏繞角度隨囊體波紋角的變化而由36.8°逐漸增加到33.0°，這樣變纏繞角度的簾線纏繞工程上實現困難。

將表1中參數代入式(5) ～ (7)，利用MATLAB數值積分函數trapz進行計算，可得等效平衡纏繞角的環向和軸向計算結果，環向計算結果如圖5所示，軸向計算結果如圖6所示。

從積分結果可見，當選取的等效平衡纏繞角為35.1°時，囊體的環向變形量為0 mm；當選取的等效平衡纏繞角在[34.6°, 35.6°]的范圍內時，囊體環向變形量在1 mm以內。當簾線纏繞角度在[34.9°, 35.0°]的范圍內時，在囊體波紋角φ的全取值范圍內，囊體的半徑增量半分比η都小于5%。綜上分析，為保證氣囊隔振器按照等效平衡纏繞角纏繞時囊體變形最小，具有最佳的平衡性，可選取35°為本文算例氣囊的最優等效平衡纏繞角。

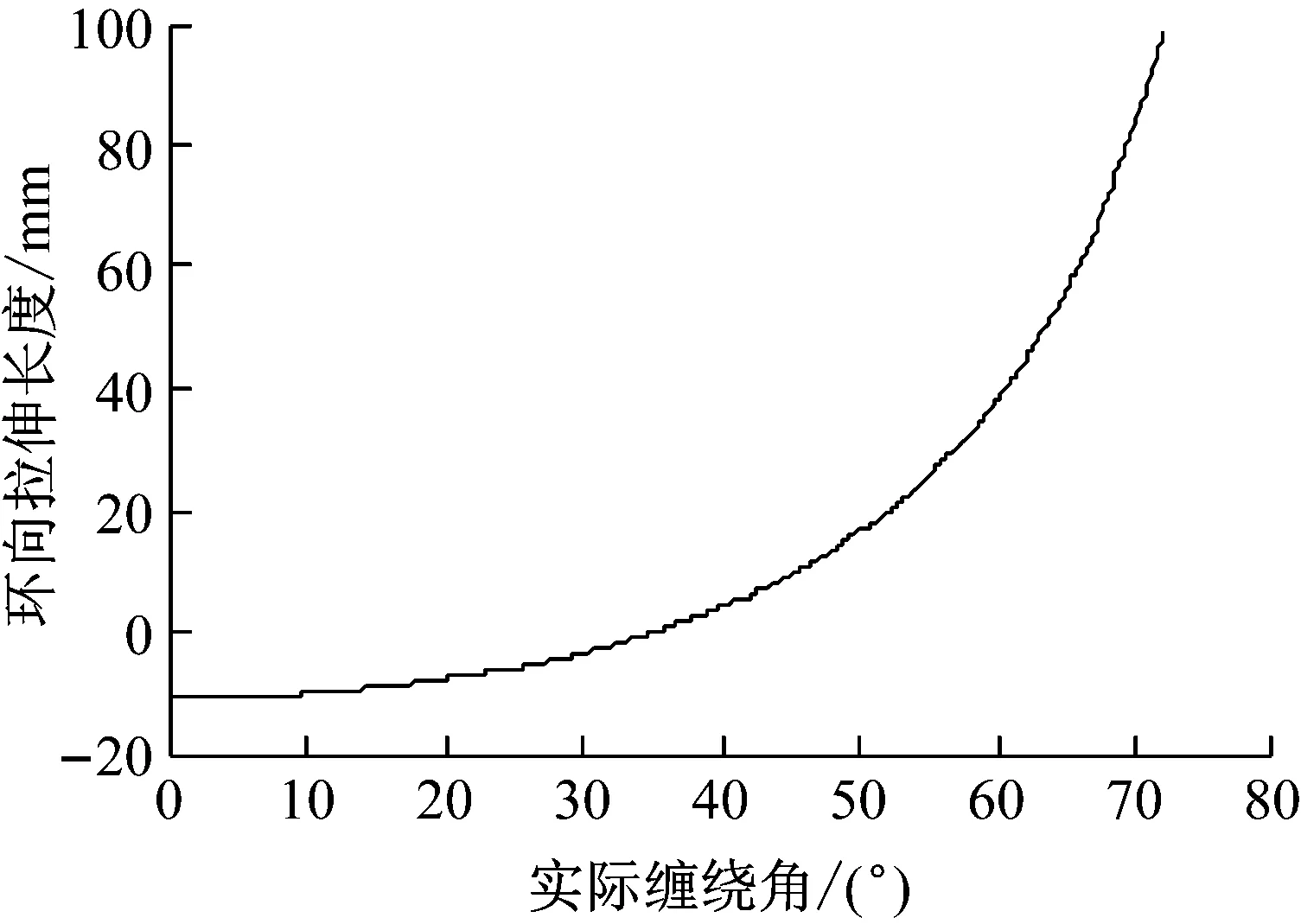
圖5 簾線纏繞角與環向拉伸長度關系示意圖Fig.5 Relationship between winding angle and circumferential tensile elongation

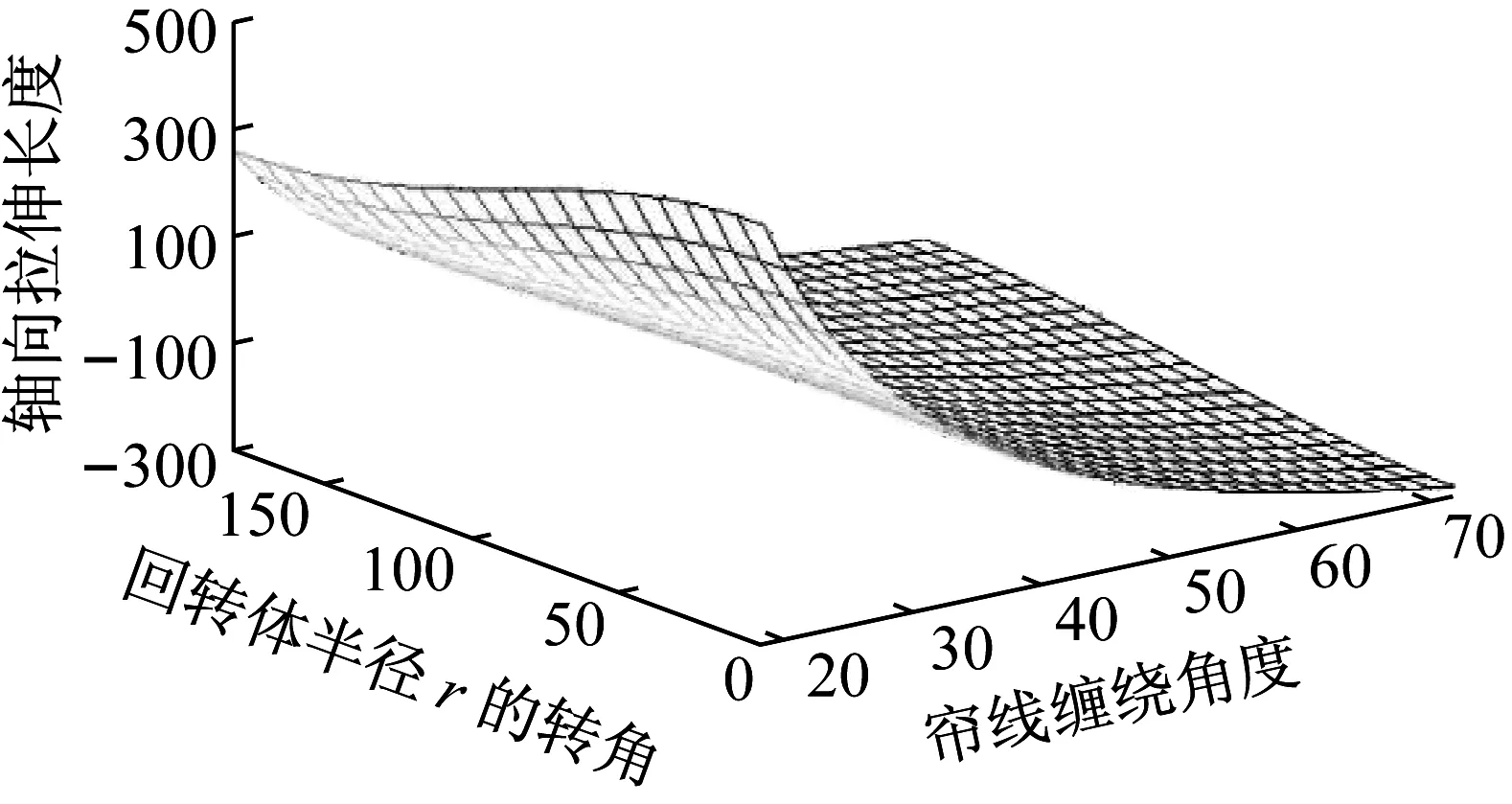
圖6 軸向伸長量計算結果Fig.6 Result of the axial tensile elongation

2 有限元仿真

2.1 平衡性仿真

通過建立算例氣囊下側回轉體部分有限元仿真分析模型，對等效平衡纏繞角理論開展仿真驗證。利用MARC軟件的rebar功能仿真囊壁的簾線層，通過設置不同纏繞角度，分析囊壁變形趨勢。使用軸對稱模型進行仿真分析，分析結果如圖7所示。

將不同簾線纏繞角度時，有限元模型中囊體垂向自由端平衡態位移量分析結果與輸入的簾線纏繞角度對應關系繪制曲線，如圖8所示。

從仿真分析結果可見，簾線纏繞角度為35°時，氣囊囊壁達到了最佳的平衡性。

2.2 靜態特性仿真

建立算例氣囊靜態特性仿真模型如圖9所示。為對不同簾線纏繞角度下氣囊承載特性進行仿真分析，在仿真時選取簾線纏繞角度為10°～50°，靜態特性分析計算結果如圖10所示。

分析結果表明，當簾線纏繞角度為35°時，氣囊的承載力約38 481 N，與理論計算值38 480 N幾乎相同，這表明氣囊簾線按最優等效平衡纏繞角纏繞時，其承載特性完全滿足設計要求。

通過設置位移邊界條件，可以仿真計算氣囊的靜態剛度，不同纏繞角時，氣囊的靜剛度仿真計算結果如圖11所示。

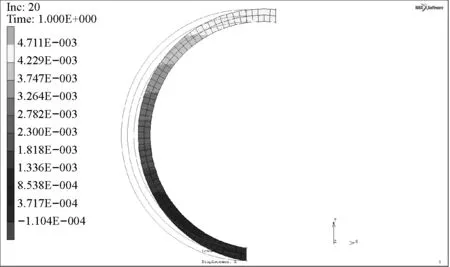
(a)纏繞角33°

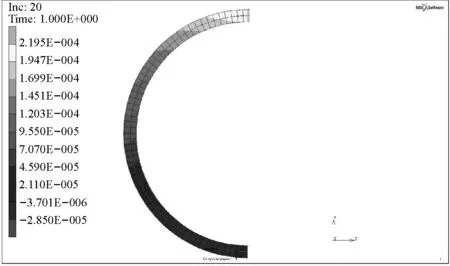
(b)纏繞角35°

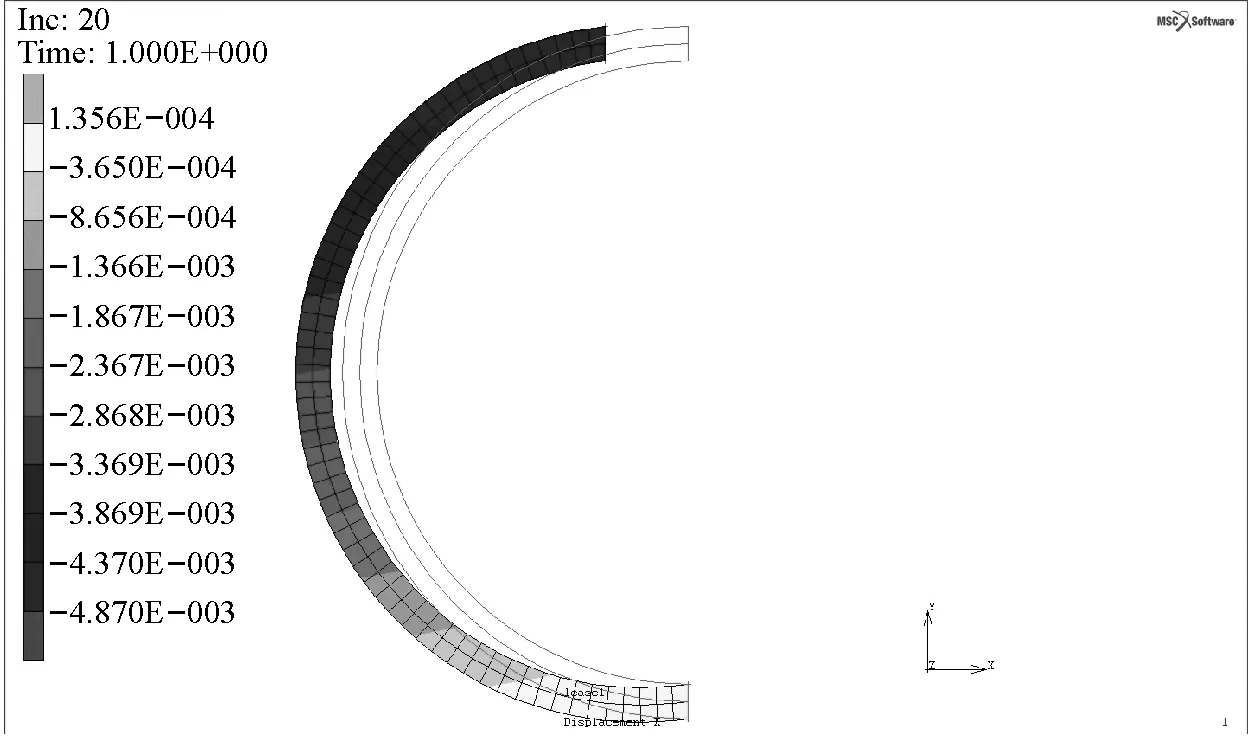
(c)纏繞角37°圖7 不同簾線纏繞角度對應的囊體變形Fig.7 Capsule’s transformation under different cord winding angles

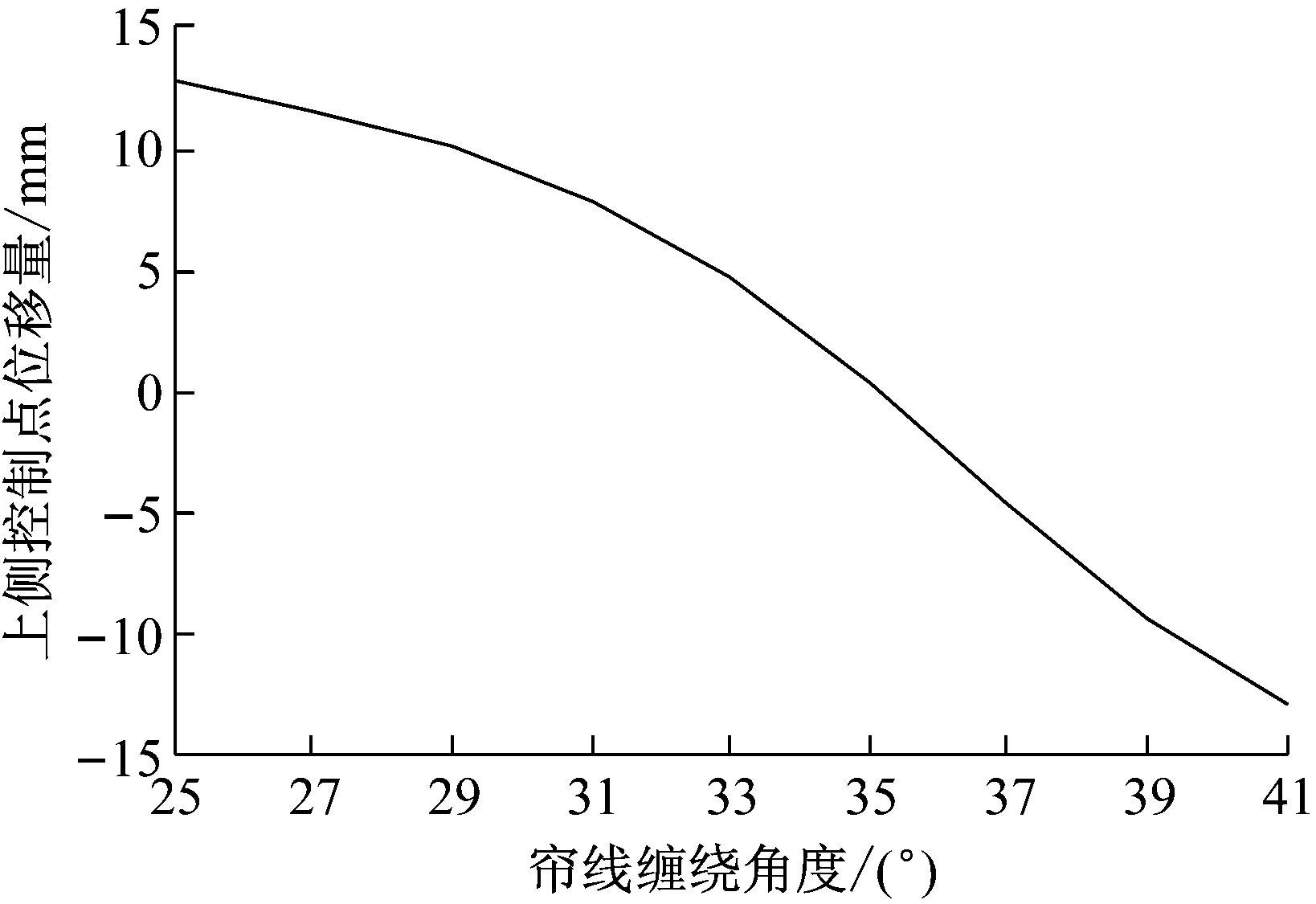
圖8 簾線纏繞角度與上控制點位移量關系曲線Fig.8 Vertical displacement of the upper control point under different cord winding angles

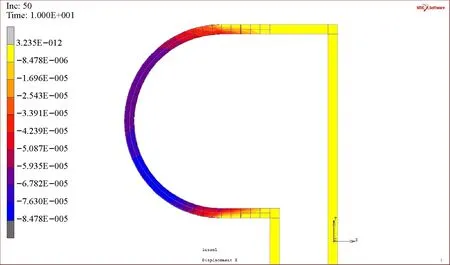
圖9 囊體靜態特性仿真模型Fig.9 Static simulation model of capsule

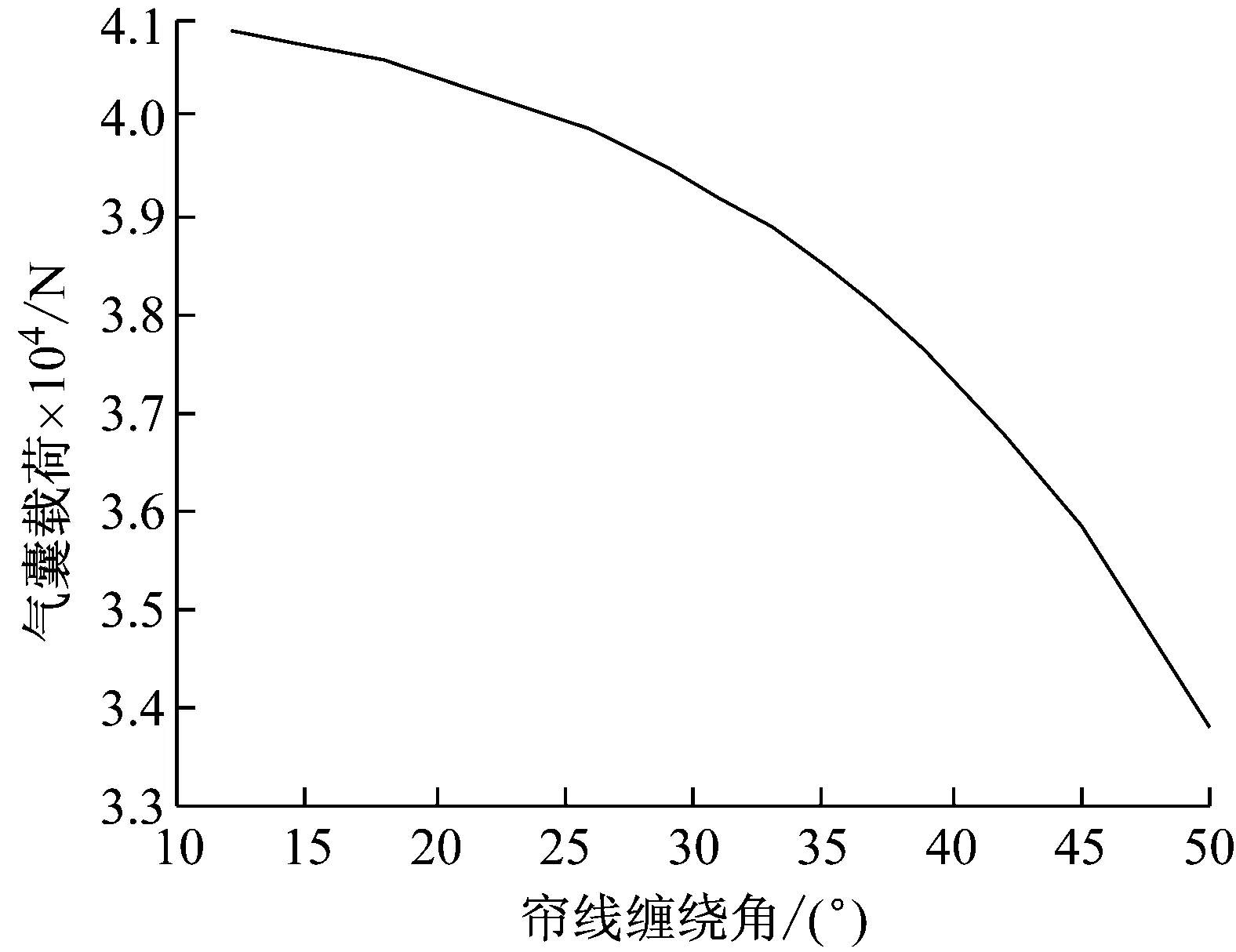
圖10 纏繞角-載荷關系曲線Fig.10 Relation curve of winding angle and load

靜剛度分析結果表明，當氣囊簾線按照等效平衡纏繞角纏繞時，其垂向靜剛度值為0.93 kN/mm，與理論計算值1.082 kN/mm存在一定差距。分析其原因，主要是仿真模型建立時，考慮到分析結果的直觀性，將囊壁厚度設置為2 mm，與算例氣囊囊壁實際厚度6 mm存在較大區別，而由于囊壁面積較大，囊壁厚度對氣囊囊體容積有一定影響(見式(2))，因此導致仿真分析模型的靜剛度值相對較低。

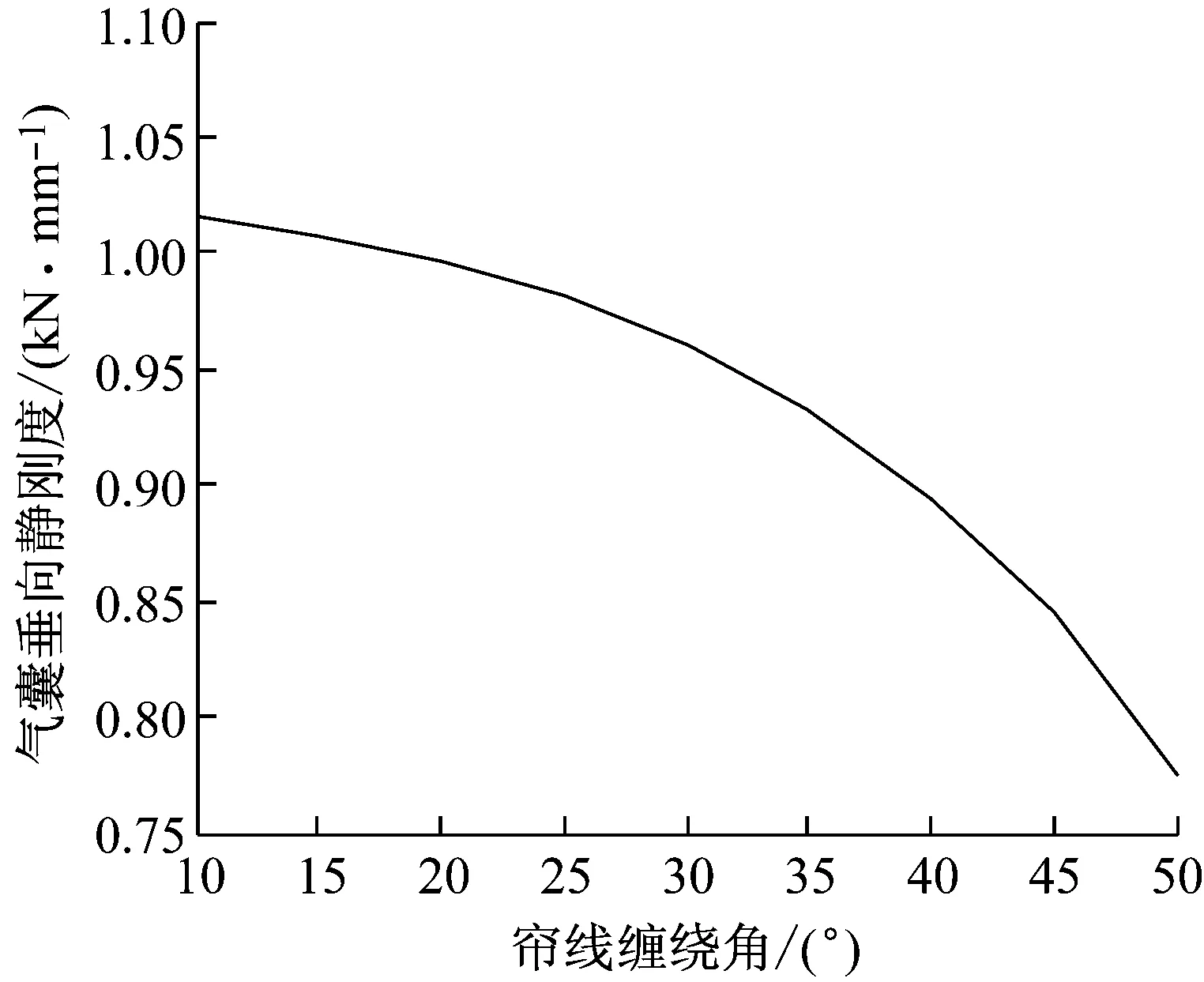
圖11 纏繞角-垂向靜剛度關系仿真結果Fig.11 Simulation analysis result of relation between winding angle and axial static stiffness

3 試 驗

3.1 囊體變形試驗

為驗證最優等效平衡纏繞角理論的正確性，設計了氣囊充氣狀態囊體變形試驗，對按35°簾線纏繞角制造的氣囊隔振器樣機進行了試驗，試驗工裝如圖12所示。

圖12 囊體變內壓下輪廓測量試驗工裝Fig.12 Equipments of capsule outline measure experiment under different pressure

試驗過程中，使用測量工裝，測量在不同囊內氣壓下，氣囊囊壁下側回轉體部分的回轉母線變形趨勢，測量結果如圖13所示。

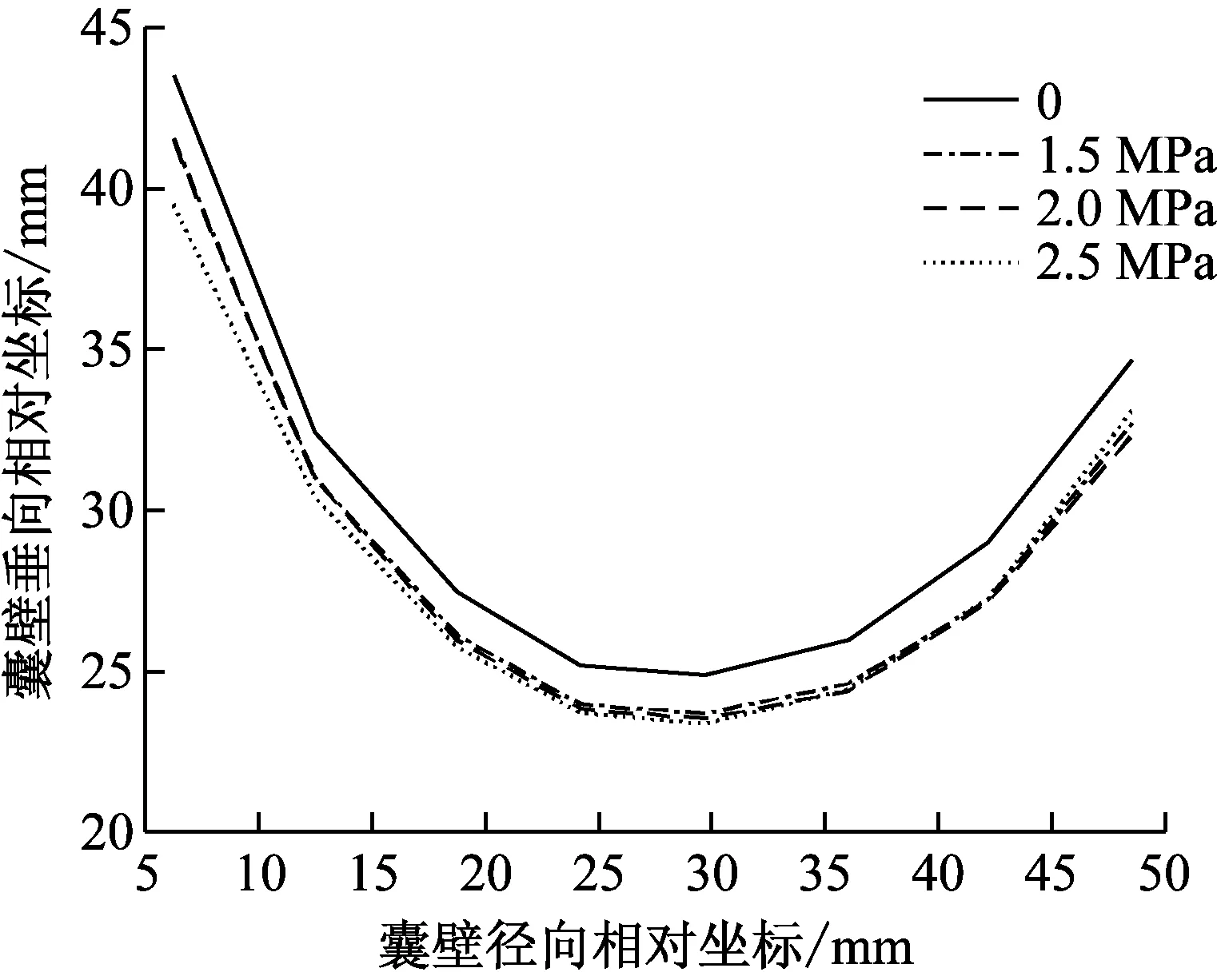
圖13 不同內壓下囊體輪廓曲線Fig.13 Capsule outline under different pressure

試驗結果表明，被試氣囊隔振器充壓后，囊體會發生一定膨脹，但是在整條回轉母線上，也即在囊壁波紋角φ處于[0,π]的范圍內，氣囊囊體變形均勻，未出現囊體不平衡時可能會出現的外傾或內傾式變形，以及局部凹陷等現象，被試氣囊隔振器囊體具有較好的平衡性。

3.2 氣囊性能試驗

為了驗證按照等效平衡纏繞角纏繞的氣囊隔振器主要性能參數與設計指標的一致性，利用MTS試驗機，對被試氣囊隔振器進行承載特性測試以及靜、動態剛度特性測試，測試工裝如圖14所示。其中，靜動態性能測試時，氣囊均充氣至2.5 MPa囊內壓力。動剛度測試時，激振峰峰值為0.8 mm，激振頻率為3.0 Hz。

圖14 氣囊垂向靜,動態性能試驗Fig.14 The RSAS’s axial static/dynamic stiffness experiment

被試氣囊隔振器承載特性測試結果如圖15所示，靜態特性測試結果如圖16所示。所有測試的數值結果見表2。

從試驗結果可見，按照最優等效平衡纏繞角纏繞的膜式氣囊隔振器樣機的承載力較設計值偏低約1 kN，究其原因，是因為承載力計算時，有效面積是按照囊體完全不發生變形的時的形狀參數進行計算的，而實際測試過程中，囊體會不可避免的發生膨脹變形，導致氣囊的形狀參數發生變化，進而影響了承載力的試驗結果；同時，也可以看到，樣機的剛度特性參數與理論計算結果吻合度非常高。在氣囊隔振器的實際使用選型中，可以通過調整囊內氣體壓力來實現承載力的可變控制。綜上，對氣囊樣機的性能參數試驗結果證明了氣囊隔振器簾線等效平衡纏繞角理論的正確性和可行性，可以用于指導工程實踐，簡化生產工藝。

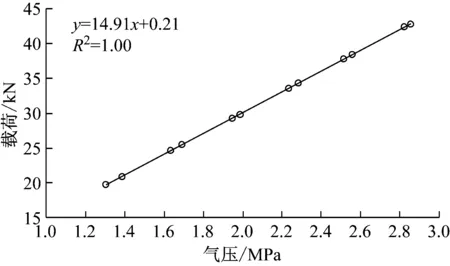
圖15 氣壓-載荷性能曲線Fig.15 Curve of pressure-load relationship

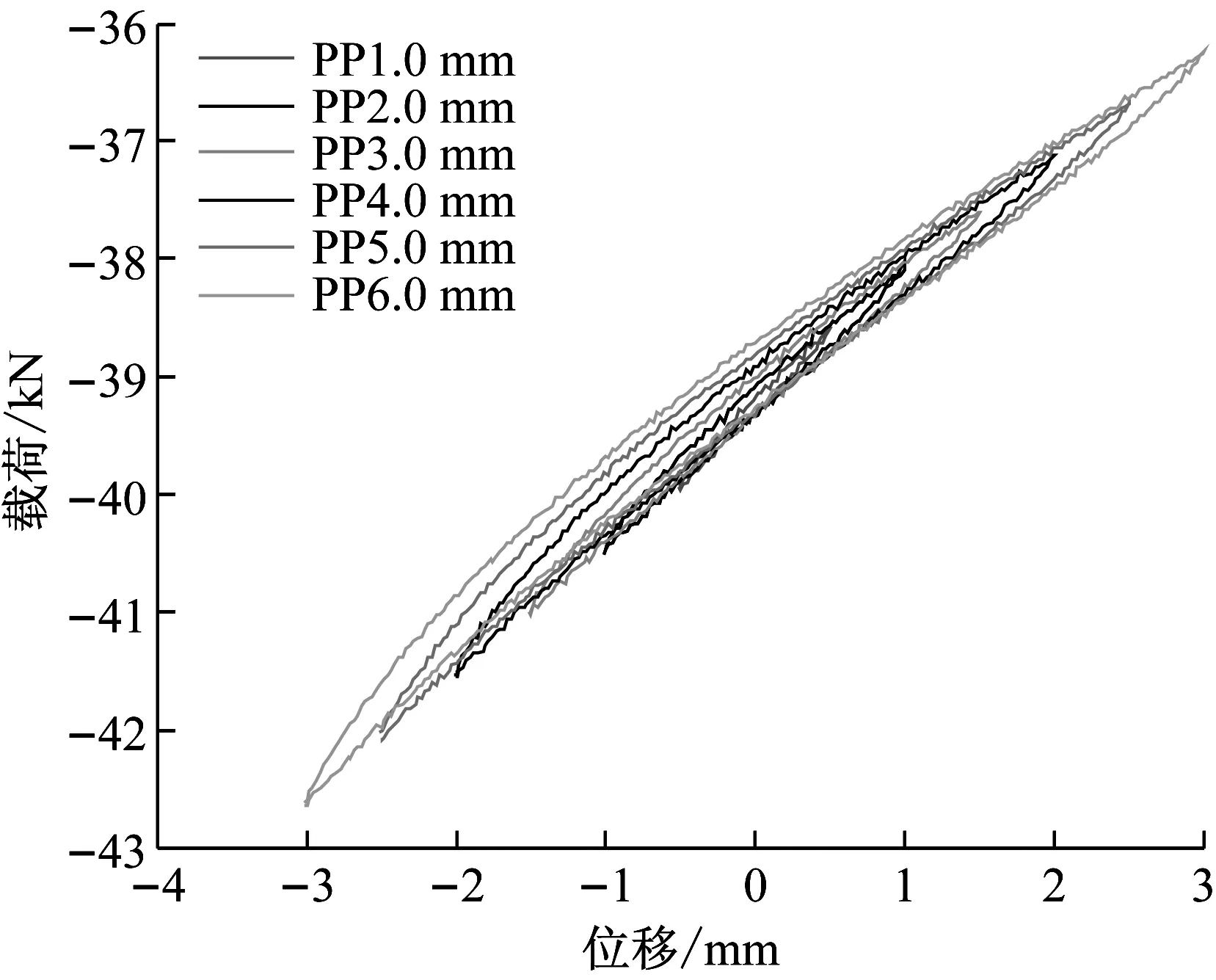
圖16 上蓋板位移-載荷特性曲線Fig.16 Curve of the upper cover-plate’s displacement-load relationship

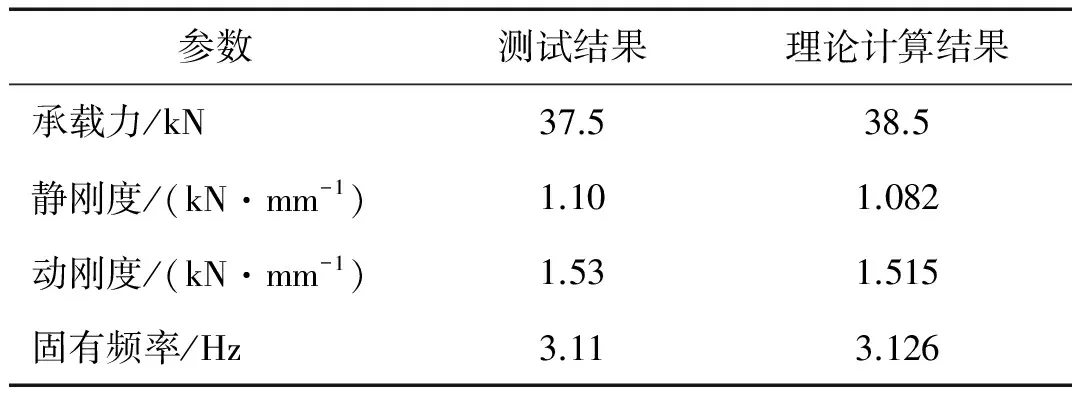
表2 氣囊隔振器主要參數試驗與理論結果對比Tab.2 Campare of main parameters of the RSAS

4 結 論

本文對氣囊隔振器的基本理論、囊體簾線平衡纏繞角理論和簾線等效平衡纏繞角理論進行了闡釋和研究。通過算例分析，給出算例氣囊隔振器的基本性能參數理論值、簾線理論纏繞角度表達式、以及囊體下側回轉體部分環向和軸向等效平衡纏繞角的計算和選取方法，并選定了算例氣囊的最優等效平衡纏繞角。通過算例氣囊隔振器的承載特性以及靜態特性的仿真分析，驗證了等效平衡纏繞角理論及其計算結果的正確性。對按照計算的簾線等效平衡纏繞角制作的氣囊隔振器樣機開展了承載試驗和靜、動態特性試驗，試驗結果表明，被試樣件的測試值與理論計算值十分吻合，證明了等效平衡纏繞角理論的正確性和工程上的可行性。

本文研究結論表明，氣囊隔振器囊體簾線等效平衡纏繞角理論對于氣囊隔振器的研制具有重要的指導意義和實用價值，可用于指導工程實踐，簡化生產工藝。

參 考 文 獻

[1] LEE J H, KIM K J. Modeling of nonlinear complex stiffness of dual-chamber pneumatic spring for precision vibration isolations[J]. Journal of Sound and Vibration, 2007，301(3):909-926.

[2] 趙應龍,呂志強,何琳.JYQN艦用氣囊隔振器研究[J].艦船科學技術,2006,28(2): 89-92.

ZHAO Yinglong, Lü Zhiqiang, HE Lin. Study of pneumatic vibration isolator of type JYQN[J]. Ship Science and Technology, 2006,28(2): 89-92.

[3] 朱石堅,何琳.船舶減振降噪技術與工程設計[M].北京：科學出版社,2002.

[4] 張立國,張嘉鐘,賈力萍,等.空氣彈簧的現狀及其發展[J].振動與沖擊,2007,26(2)：146-150.

ZHANG Liguo, ZHANG Jiazhong, JIA Liping, et al. Future and development of air springs[J]. Journal of Vibration and Shock,2007, 26(2)：146-150.

[5] 顧太平,何琳,趙應龍.囊式空氣彈簧平衡性分析[J].機械工程學報, 2011, 47(3): 69-72.

GU Taiping, HE Lin, ZHAO Yinglong. Equilibrium performance analysis for bellows type air spring[J]. Journal of Mechanical Engineering, 2011, 47(3): 69-72.

[6] 張俊玲,王浩宇.初始內壓和簾線間距對膜式空氣彈簧橫向剛度特性影響的有限元分析[J].橡膠工業,2013,60(4):233-238.

ZHANG Junling, WANG Haoyu. Effect of initial internal pressure and cords distance on lateral stiffness of rolling lobe air spring by using finite element analysis[J]. China Rubber Industry, 2013,60(4):233-238.

[7] GIUSEPPE Q，MASSIMO S. Air suspension dimensionless analysis and design procedure[J]. Vehicle System Dynamics, 2001, 35(6): 443-475.

[8] 金著. 膜式氣囊隔振器囊體結構力學特性研究[D].武漢：海軍工程大學，2014.

[9] 金著,趙應龍,何琳,等.膜式氣囊隔振器簾線纏繞角度研究[J].艦船科學技術，2015，37(12):63-67.

JIN Zhu, ZHAO Yinglong, HE Lin, et al.Research on the cord’s wound angle in reversible sleeve air spring[J]. Ship Science and Technology, 2015, 37(12):63-67.

[10] 趙應龍,金著,何琳.氣囊隔振器囊壁骨架層平衡性研究[J].船舶力學，2017，21(7):873-879.

ZHAO Yinglong, JIN Zhu, HE Lin. Research on framework layer’s equilibrium performance of air spring capsule[J]. Journal of Ship Mechanics, 2017, 21(7):873-879.