基于沖擊回波的原木內部空洞位置檢測方法研究

梁 臣， 馮海林， 方益明， 李 劍(1.浙江農林大學 信息工程學院，杭州 311300；2.浙江省林業智能監測與信息技術研究重點實驗室，杭州 311300)

無損檢測作為一種直接、準確、客觀的方法,滿足木材生產中非破壞性快速檢測和持續檢測的需要而越來越受重視。國內外已在此方面做了大量的研究工作,在將超聲波、射線、微波等無損檢測技術應用到木材物理性質、生長特性及木材缺陷等方面取得了一定的成績,研究出多種無損檢測手段,并通過實驗取得了較好的成果[1-3]。但射線、微波檢測方法所需設備價格昂貴；相同條件下，超聲波在原木中的衰減比應力波更快[4]，所以應力波在原木中的適應性更強。

目前，國內外在使用應力波對樹木內部的缺陷已經進行了較廣泛的研究。梁善慶等[5]通過應力波傳感器波速矩陣重構所得斷層二維圖像能夠直觀顯示缺陷部位、大小及形狀等信息；王立海等[6]發現使用應力波斷層成像技術時，若需對原木缺陷進行精確測量，至少需12個傳感器才能滿足要求；僅需要判斷原木是否存在缺陷時，選用6個傳感器就能滿足要求。余觀夏等[7]運用應力波技術分析了原木橫截面中的頻譜曲線，通過頻譜曲線下的面積和一定頻率范圍的面積可計算木質材料的好壞。

沖擊回波法是20世紀80年代中期發展興起的一種無損檢測方法，通過分析應力波在物體內部的反射情況，能根據應力波信號特征檢測物體內部缺陷，具有適應性強、反應快、操作簡便、造價低等特點。該方法在混凝土、樁基缺陷的檢測當中應用比較廣泛[8-9]，而在原木檢測中的應用較少。

原木中的應力波信號有表面波、縱波、橫波等成分，但是各成分之間特征差異較大[10]。本文在現有的應力波檢測基礎上提出一種基于原木應力波信號分解的沖擊回波法。首先將應力波信號分解成多個平穩的、幅度和頻率受調制的固有模態函數(IMF)分量，然后找出對空洞敏感的IMF，最后根據該IMF的頻域特征實現原木內部空洞徑向缺陷定位。

1 基于原木應力波信號分解的沖擊回波法

1.1 沖擊回波法

應力波在整個原木軸向的傳播過程可用一維桿進行分析[11]，原理如圖1，小錘敲擊物體截面時產生縱波(P 波)、橫波(S波)、表面波(R波)。P波又稱Primary wave，傳播方向與質點震動方向一致，即與小錘的敲擊方向一致，P波是物體內傳播最快的一種應力波。S波作為一種橫波，特點是質點的振動方向與它的傳播方向垂直，因此S波的傳播時候會形成波峰和波谷。S波的傳播速度次于P波。R波是一種在物體表面傳播的應力波，R波能量較大，但衰減較快。P波在敲擊面和空洞之間來回反射形成瞬態共振，通過傳感器獲得敲擊點附近的振動信號，對振動信號進行FFT運算后可得共振的頻率，若知應力波在物體中的傳播速度，則空洞與敲擊端的距離為

(1)

式中：CP為P波傳播的速度；f為P波的峰值頻率；b為修正系數，取值為0.96[12]。通過此式可對缺陷位置做出預測。

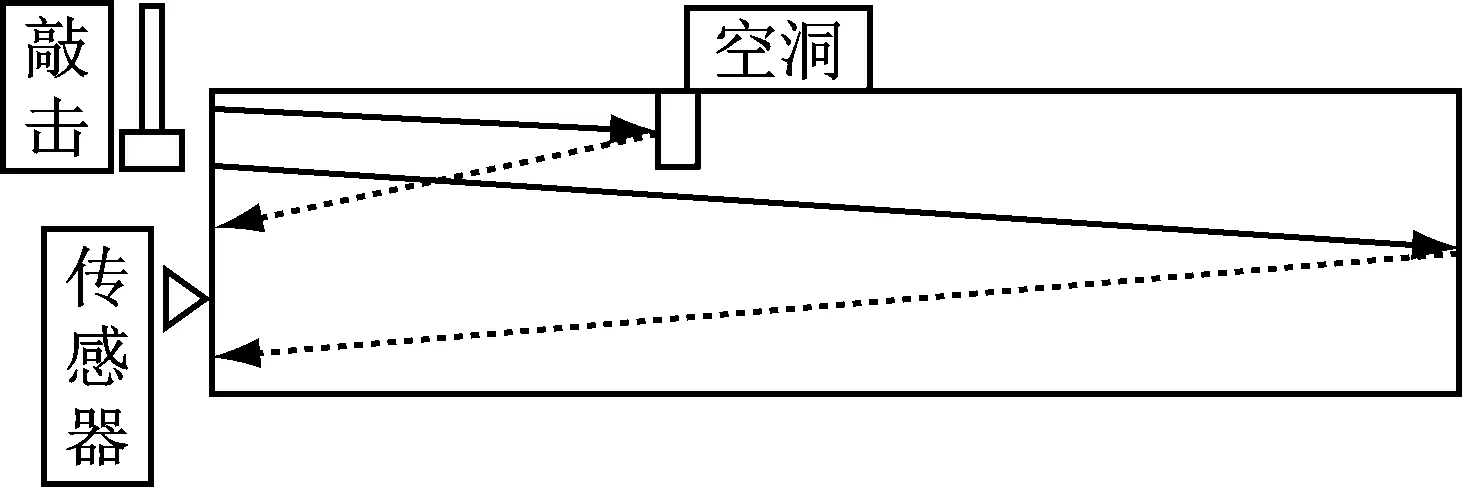
圖1 沖擊回波法Fig.1 Impact-echo method

1.2 經驗模態分解

沖擊回波信號可能包含強烈的表面波,這是一個寬頻率范圍的間歇信號。然而，經典的傅里葉變換方法只能處理線性和平穩信號，包括應力波在內的許多實際采樣信號(模型)是非平穩的或非線性的。短時傅里葉變換、小波變換等分析方法均采用固定的核函數，對信號缺乏自適應性，導致分析結果往往失去實際物理意義而不能正確提取信號本質特征[13-14]。

經驗模態分解(Empirical Mode Decomposition，EMD)適合于非線性、非平穩信號分析，其本質是對信號進行平穩化和線性化處理，把復雜的信號分解成有限個瞬時頻率有意義、幅度或頻率受調制的本征模態分量(Intrinsic Mode Function，IMF)和一個殘余函數，即

(2)

式中：r(t)為殘余函數，它是一單調函數，Ci(t)為各個IMF分量，并滿足以下兩個條件：① 在整個數據段，極值點的個數和零交叉點的個數必須相等或相差不能超過一個;② 在任何一點，由局部極大值點形成的包絡線和局部極小值形成的包絡線的平均值為零。

1.3 基于原木應力波信號分解的沖擊回波法

當應力波信號的時間尺度存在跳躍性變化時,對信號進行EMD分解,會出現一個IMF分量包含不同時間尺度特征成分的情況。在分解時為了解決這種情況，法借鑒集合經驗模態分解(EEMD)，本文提出基于原木應力波信號分解的沖擊回波(流程如圖2)步驟如下:

圖2 基于原木應力波信號分解的沖擊回波法Fig.2 Impact-echo method based on stress wave signal

步驟1 向采集的原木沖擊回波信號S(t)中加入正態分布白噪聲得到帶有白噪聲的信號x(t)。

步驟2 確定信號x(t)的所有局部極值點，通過三次樣條函數求取其上包絡u1(t)和下包絡u2(t)的局部均值

(3)

步驟3 令h(t)=x(t)-m(t)，如h(t)不滿足IMF條件，則視其為新的x(t)。重復k次得

h1k(t)=h1(k-1)(t)-m1k(t)

(4)

經過n次迭代滿足1.2節中兩個條件得到的hn(t)即為有效IMF,剩余信號則進入下一輪篩選過程。

步驟4 重復步驟1～步驟3每次加入新的白噪聲序列，將每次得到的IMF集成均值作為最終分解結果。

步驟5 剔除IMF集合中的白噪聲和表面波。

步驟6 計算各個IMF與S之間的互相關系數R

(5)

RSy(τ)為x和y信號的互相關系數，y為步驟4得到的IMF，T為信號長度，τ為時間間隔。剔除相關系數低于0.3的IMF分量。

步驟7 對剩下的IMF進行傅里葉變換，根據IMF的頻域特征結合式(1)計算缺陷位置。

1.4 基于時域特征和分量相關系數的IMF選擇方法

由于算法中應力波信號分解加入了高斯噪聲，且應力波信號中包含表面波，所以原信號分解后會有一個或多個IMF與噪聲或表面波信號特征相似，可從IMF的時域信號特征識別噪聲或表面波。

EMD分解不可避免的會出現過多分解現象，即得到的分量個數比原信號實際組成分量多，也即出現所謂的虛假分量。一般來說，信號越復雜，虛假分量的個數可能會越多，對后續信號的時頻譜分析和進一步的處理越會產生不利影響。原則上，經EMD得到的各個模式分量ci(t)應分別對應于原信號各實際組分，然而由于前述原因，兩者之間總存在誤差，其差值即形成虛假分量。分析可知，各分量雖不等同實際組分，但必是后者的近似，即兩者存在一定的相關性;而虛假分量由兩者差值形成，相關性必然很小。因此，從各分量與原信號相關分析中應能分辨出其真偽。

2 噪聲參數選擇

加入白噪聲的幅度和數量是分解的兩個關鍵參數。通過實驗觀察，加入足夠多的白噪聲集合數量能使分解以后信號的噪聲變得緩和，并建議在大多數情況下添加噪聲的振幅與原信號的標準差比值為0.2[15-17]，但研究內容專注于從振幅相對較小的間歇信號中提取高頻與低頻連續信號。在沖擊回波信號中包含強連續性的縱波信號和能量較強的間歇性表面波，這和上述信號有著不同的特征，也因為表面波擁有的較寬的頻率帶寬導致縱波的提取比較困難。

為了研究噪聲參數設置在沖擊回波應用中的效果, 利用有限元建立木材模型，模擬一個信號來表示沖擊回波中原木表面質點的平面外位移測試。模擬應力波在木材中的傳播已有一些研究，如利用有限元法模擬木材材料性質和缺陷對應力波傳播的影響[18]，應力波在木材橫切面的傳播過程[19]等。本文則假設原木紋理與原木軸向平行，將原木看作一種正交各向異性材料。在有限元仿真軟件ANSYS中選取正交各向異性單元Solid185作為建模單元，以松木為建模原型建立三維原木模型。沖擊源為一個半徑0.02 m的鐵球，鐵球以10 m/s的速度縱向沖擊模型A端，沖擊點離模型A端圓心0.07 m，在徑向離沖擊點0.14 m處采集質點加速度模擬縱波信號，采樣頻率0.1 MHz，沖擊點和信號采集位置如圖3,采集的信號如圖4(a)。[20]

圖3 信號采集和沖擊位置Fig.3 Signal acquisition position and impact position

基于有限元分析中沖擊回波模型[21]選取表面波函數

y(t)=Aλ(sin(πx/η))3(u(t)-u(t-η))

(6)

A為表面波與縱波的振幅比例，λ為縱波的幅值，x為縱波信號，u(t)為赫維賽德階躍函數，η為沖擊持續時間，取1 ms(如圖4(b))。縱波與表面波混合信號如圖4(c)。

(a) 縱波信號

(b) 表面波信號

(c) 混合信號圖4 有限元仿真模擬原木沖擊回波信號Fig.4 The log impact echo signal by finite element simulate

使用分解以后的IMF與縱波的相關系數作為衡量標準。人工設定噪聲幅度與沖擊回波標準差比例0，0.1，0.2，0.5，0.7，1，1.2，1.5，2，2.5和3；噪聲數量從10～200，每次遞增10。

添加不同的噪聲幅度對相關系數的影響如圖5(a)所示，當A=1時，添加較小的噪聲比例(0.1)能讓分解后的IMF與原沖擊回波信號相關系數達到較高的程度(0.95)。當表面波的幅度增加，A=3，5，8時，添加較高的白噪聲幅度(與沖擊回波信號標準差比例為2)也能使相關系數達到較好的效果，分別為0.937，0.910，0.895。

盡管添加比較多的噪聲數量能夠影響EEMD分解的效果，但是添加太多數量的噪聲也耗費較多的時間。不同的噪聲數量對EEMD方法分解效果影響如圖5(b)所示，當A=1時，添加噪聲數量從20以后，相關系數開始趨向收斂。當A=3，5，8時，添加噪聲數量從80以后，相關系數值也趨向穩定。

結果表明，即使在有較強表面波和噪聲的情況下依舊能分成很多模態，設置合適的EEMD參數能夠使得到的IMF與縱波信號接近。

(a) 噪聲幅度與沖擊回波標準差比例

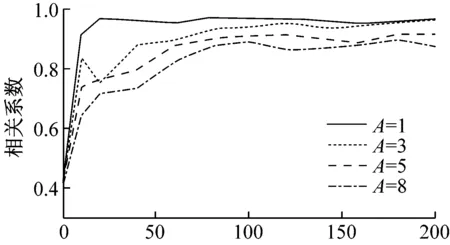
(b) 噪聲數量

圖5 添加不同的噪聲幅度和數量對EEMD分解后的IMF與P波之間相關系數的影響

Fig.5 Adding up the amplitude and number of different noises sees the effects on the correlation coefficient between IMF and longitudinal wave

3 試驗分析

3.1 試驗設備與材料

選取兩棵雪松和一棵白楊健康原木，尺寸分別為1#雪松1.9 m，含水率36%，大小端直徑分別為19 cm和22 cm；2#白楊2.32 m，含水率42%，大小端直徑分別為20 cm和24 cm；3#雪松2 m，含水率40.5%，大小端直徑分別為23 cm和26 cm。使用FAKOPP Microsecond Timer微秒計測出兩端之間的傳播時間，根據原木長度計算出波速。將原木分AB兩端置于水平地面，距離1號原木A端1 m、2號A端0.7 m、3號A端0.3 m處鑿開空洞，空洞尺寸從0.08×0.08 m、0.1×0.1 m、0.12×0.12 m逐漸擴大。用鐵錘敲擊原木A端，敲擊過程中把握力度保證每次敲擊力度差別不大，敲擊點離原木髓心0.07 m，在敲擊點徑向0.14 m處垂直釘上加速度傳感器，傳感器型號為蘭德BZ1105，示波器采樣頻率為0.25 MHz，B端按同樣的方式測試。實驗平臺、原木模型尺寸、空洞大小與位置分別如圖6、圖7、圖8所示。

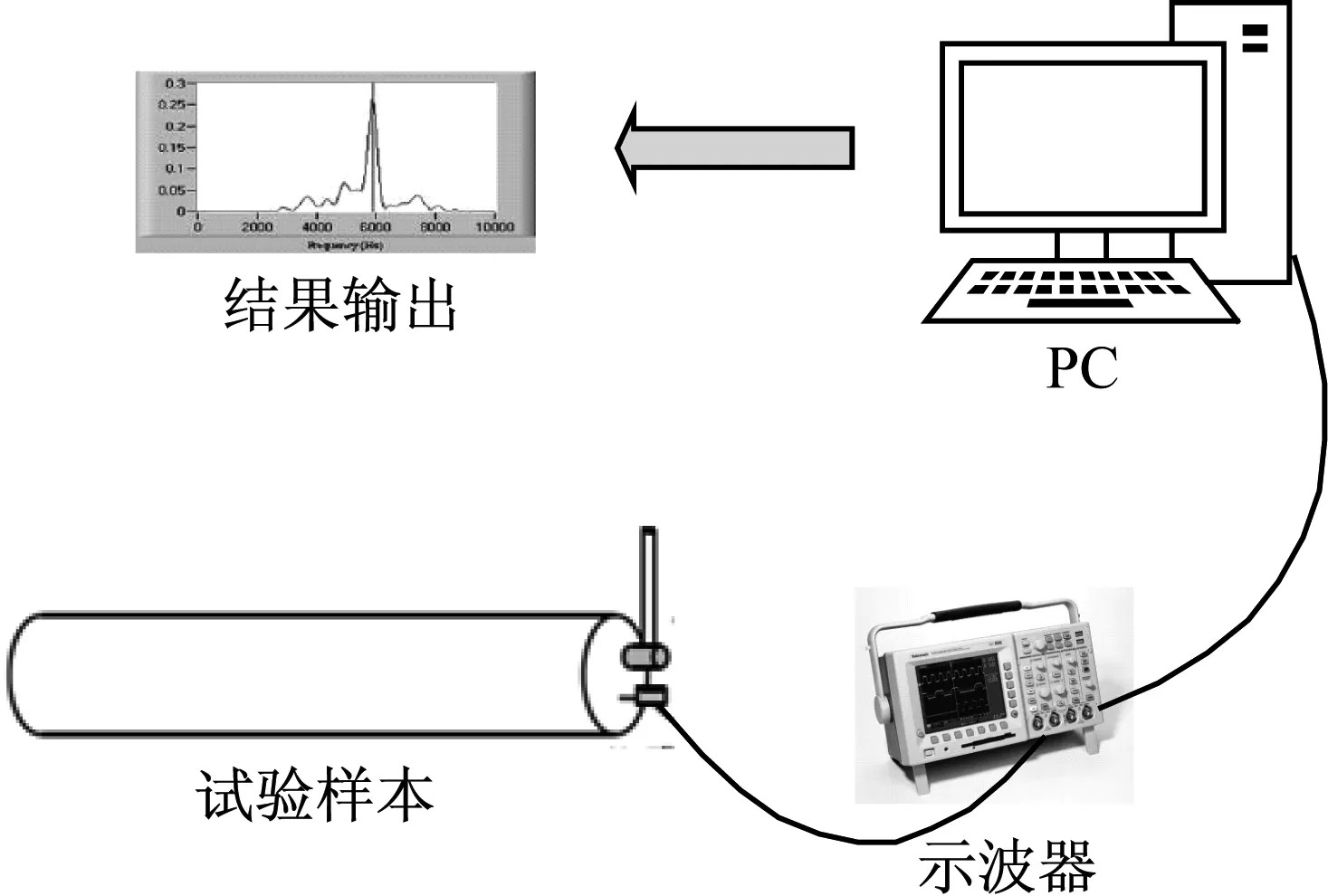
圖6 試驗平臺示意圖Fig.6 Test platform

圖7 原木及各空洞尺寸(cm)Fig.7 Logs and different size holes(cm)

圖8 原木模型及空洞位置示意圖Fig.8 Models of logs and location of holes

3.2 試驗結果分析

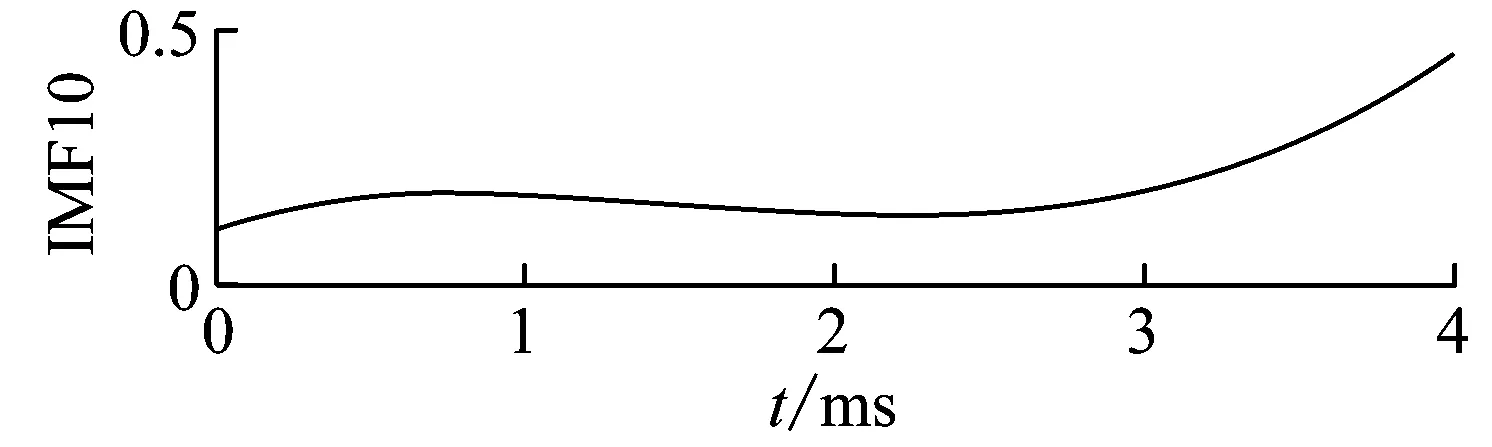
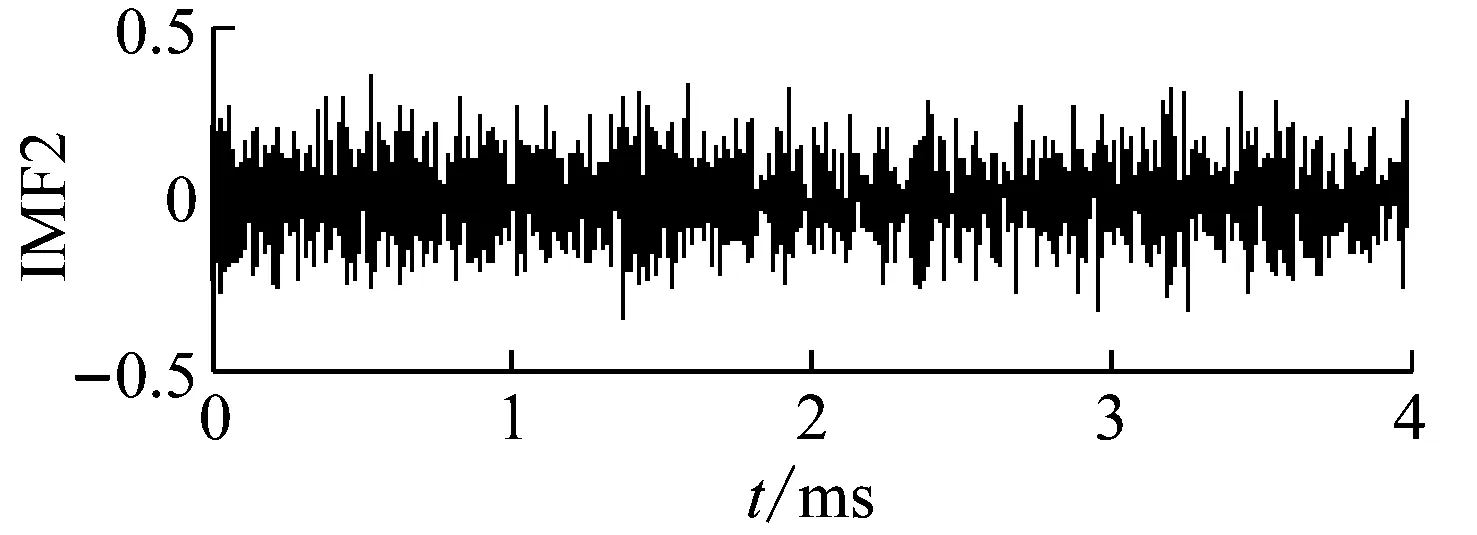
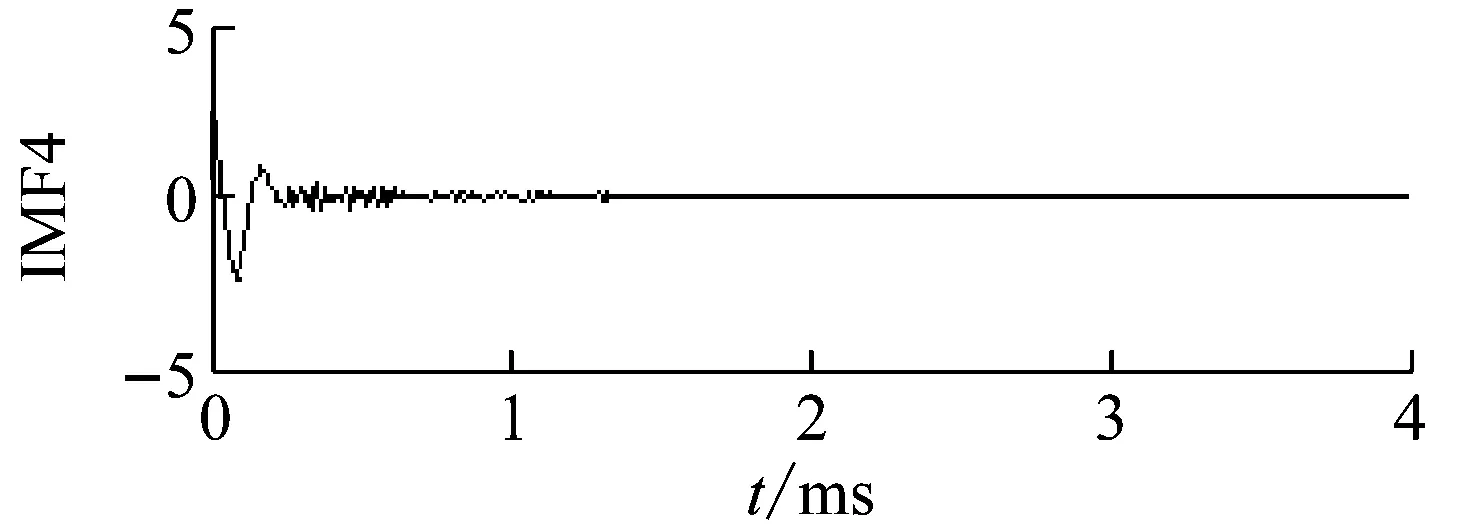
分別對1～3號原木兩端施加沖擊，采集不同尺寸空洞的測試信號，1#原木空洞尺寸0.08 m×0.08 m時，沖擊回波信號如圖9(a)。對信號進行分解，添加噪聲的幅度標準差比例為2，噪聲數量為100，分解結果如圖9(b)。從圖中觀察可看出IMF1～2明顯為頻率較高的白噪聲。IMF3幅值較高的波峰均在0.2 ms以內，且衰減較快，與表面波信號特征相似；IMF10為殘余分量，在分析時應以剔除。

(a) 沖擊回波采集信號

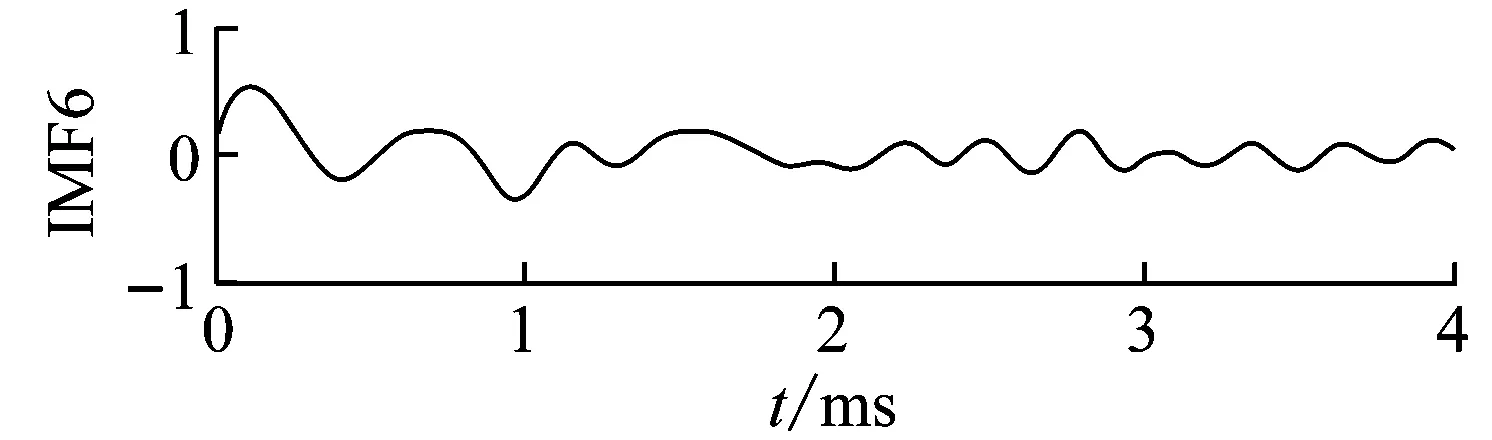
(b) 沖擊回波信號分解結果圖9 1#原木0.08 m×0.08 m空洞尺寸下A端應力波信號

Fig.9 The 0.08 m×0.08 m hole size log Stress wave signals of No.1 log model in endA

通過各IMF與原信號互相關系數表中(表1)可看出IMF6～9與原信號相關度都在0.3以下，屬于虛假分量。IMF4和IMF5與原信號相關性較高，并擁有連續性縱波特征，信息可用于計算。對IMF4和IMF5進行傅里葉變換，結果如圖10，然后通過IMF4頻域譜峰值2 040 Hz和IMF5頻域譜峰值1 120 Hz代入式(1)，計算結果分別為0.957 m對應缺陷位置誤差4.3%和1.855 m對應原木末端位置誤差2.4%。

圖10 1#原木基于時域特征和分量相關系數相結合選擇出IMF頻域信號

Fig.10 IMF frequency domain signal in No.1 log selects by the combination of the time domain characteristics and component correlation coefficient

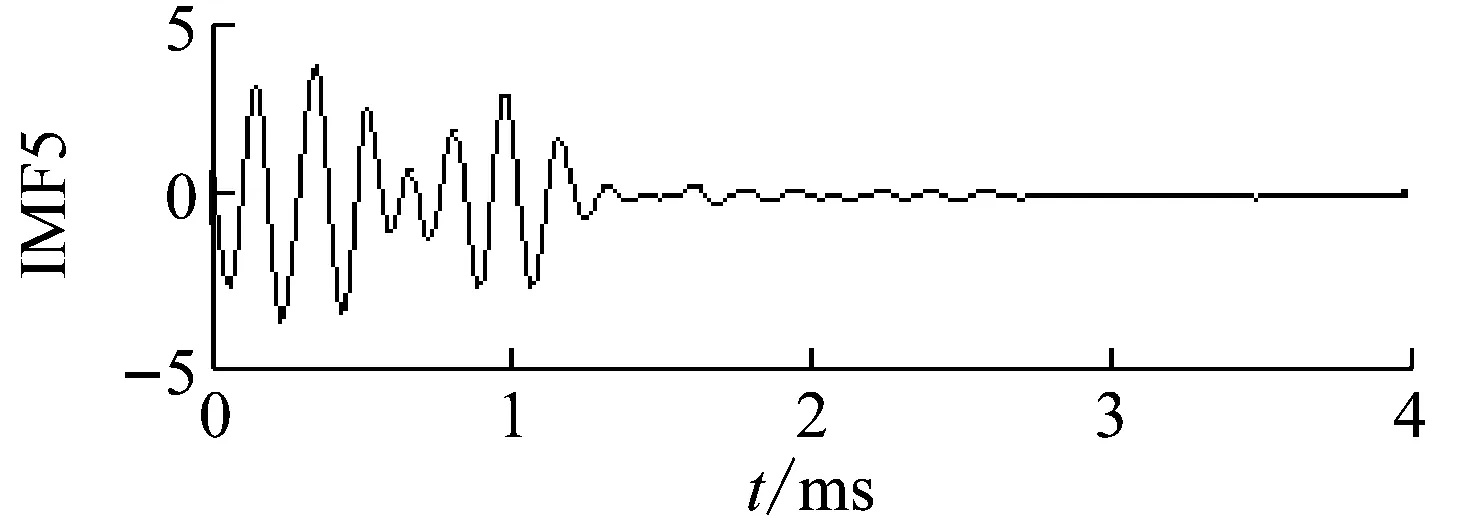
2#原木沖擊回波信號在1 ms內沒有較大的衰減(圖11(a))，添加噪聲幅度比例0.1、數量100，分解結果如圖11(b)。與1#原木情況相似，IMF1～3為白噪聲、IMF4為表面波、IMF10為殘余分量、IMF7～9的相關系數較低，通過IMF5的頻域特征計算缺陷位置為0.71 m，誤差1.4%。

由表2可知，利用本文方法計算1#和2#兩端、3#B端缺陷位置誤差均在10%以內，可準確的判斷出空洞位置。當空洞距離檢測端0.3 m情況下，3#原木A端檢測誤差較大，其原因為空洞距離原木末端較近，沖擊波在空洞和原木末端發生多次反射形成共振，反射波形成的共振頻率大于沖擊信號的頻率造成，當鐵球撞擊原木端面時，撞擊點振動形成入射波，當入射波的頻率小于共振頻率后，測試就會不準確[22]，但可從B端檢測出空洞位置。并且從表1中可看出對缺陷敏感的IMF與原信號的互相關系數隨著空洞的擴大也逐漸增加，這是由于空洞反射面擴大，反射的應力波在采集的信號中占有比例也隨之增加。

(a) 2#白楊原木0.08 m×0.08 m尺寸空洞A端應力波時域信號

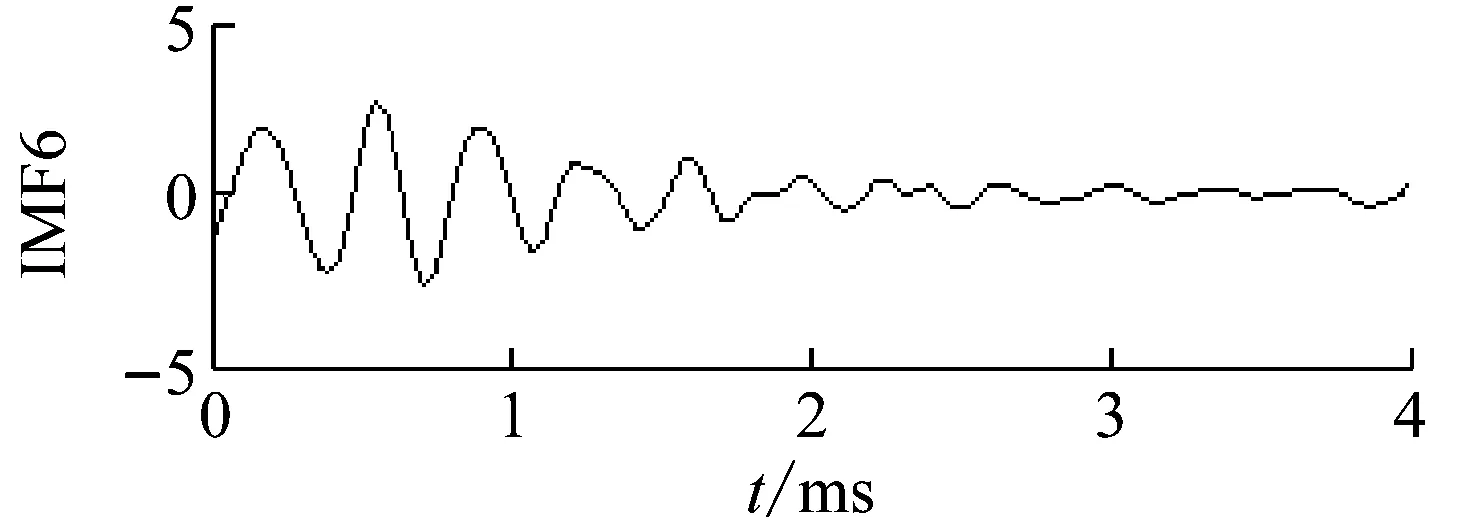
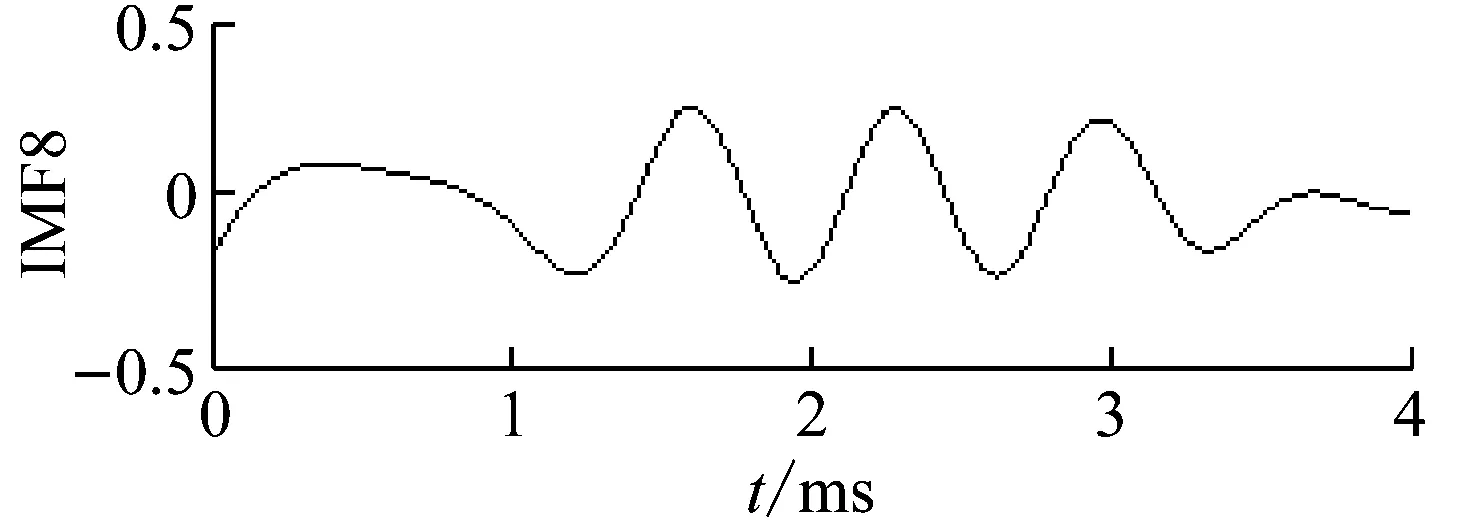
(b) 沖擊回波信號分解結果圖11 2#白楊原木0.08 m×0.08 m空洞尺寸下A端應力波信號Fig.11 The 0.08 m×0.08 m hole size log Stress wave signals of No.2 log model in end A

圖12 2#原木基于時域特征和分量相關系數相結合選擇出IMF頻域信號Fig.12 IMF frequency domain signal in No.2 log selects by the combination of the time domain characteristics and component correlation coefficient

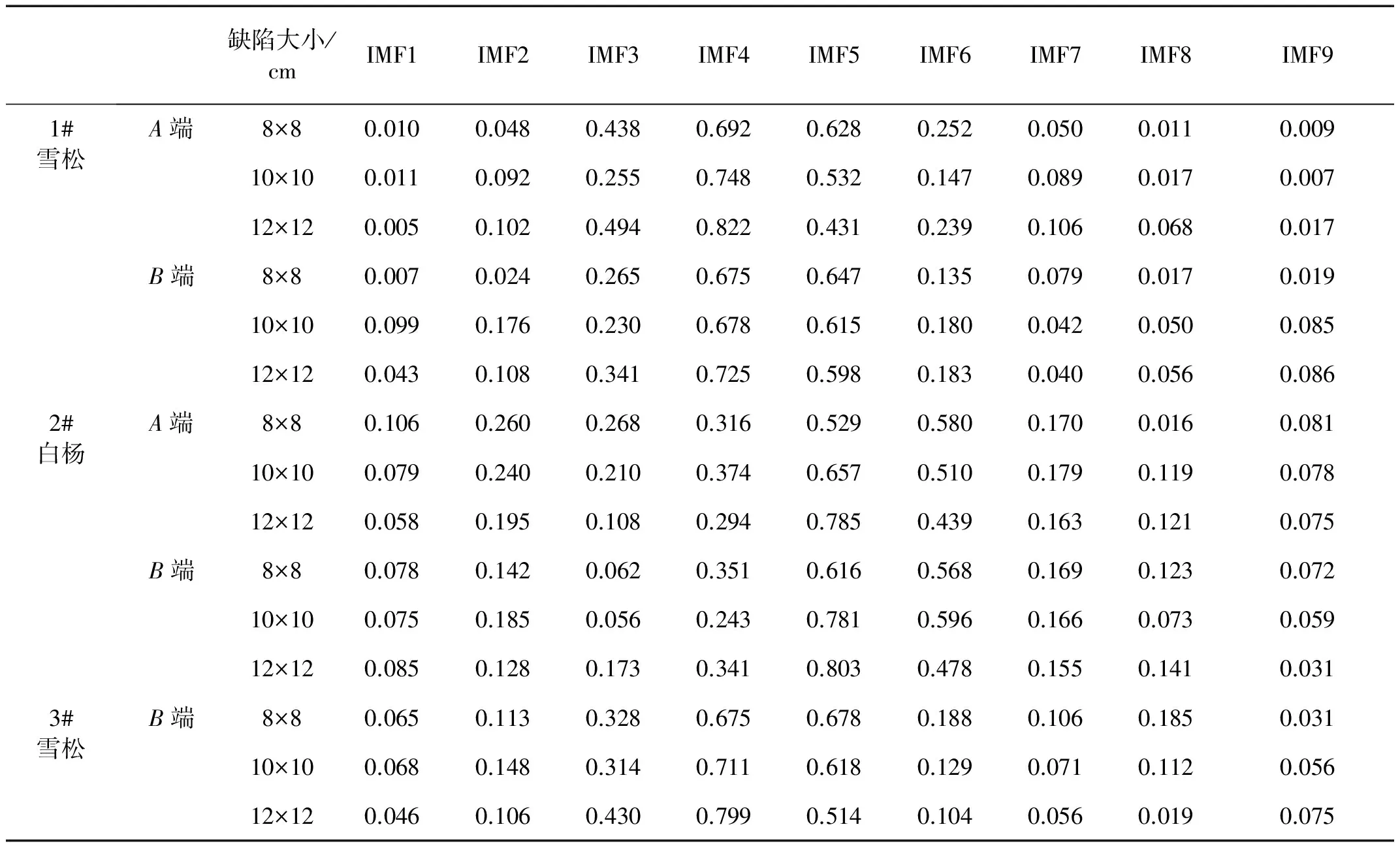
表1 各IMF與沖擊回波信號相關系數Tab.1 Correlation coefficient between IMF and Impact-echo signal

表2 原木樣本檢測結果Tab.2 Log sample test results

4 結 論

本文提出了一種基于原木應力波信號分解的沖擊回波法，用于原木徑向空洞檢測。通過有限元仿真模擬原木中應力波信號得出：設置合適的EEMD參數能夠使得到的IMF與縱波信號接近，在有較強表面波和噪聲的情況下需要添加的噪聲數量較多、標準差比例較大。選擇空洞位置和大小不同、長度不同的原木樣本試驗，驗證了該方法的可行性。空洞距離檢測端較近的情況下(0.3 m)準確率較低，需要進一步研究。對空洞敏感的IMF分量與沖擊回波信號的相關系數和空洞大小的變化成正相關。

參 考 文 獻

[1] ROSS R J, ZERBE J I, WANG X P, et al. Stress wave nondestructive evaluation of Douglas-fir peeler cores[J]. Forest Products Journal, 2005, 55(3): 38-43.

[2] WACKER J P, WANG X, ROSS R J, et al. Condition assessment of historic wood vessels[C]∥Proceedings of the 15th International Symposium on Nondestructive Testing of Wood. Duluth, MN, 2007.

[3] WANG, X. Effects of size and moisture on stress wave E-rating of structural lumber[C]∥Proceedings of the 10th World Conference on Timber Engineering. Miyazaki, Japan, 2008.

[4] 徐華東，王立海,游祥飛,等. 應力波和超聲波在立木無缺陷斷面的傳播速度[J].林業科學, 2011, 47(4):129-134.

XU Huadong, WANG Lihai, YOU Xiangfei, et al. Propagation velocity of stress wave and ultrasonic wave transmitting on indefectible cross section of standing trees[J]. Scientia Silvae Sinicae, 2011, 47(4):129-134.

[5] 梁善慶，趙廣杰,傅峰. 應力波斷層成像診斷木材內部缺陷[J]. 木材工業, 2010, 24(5):11-13.

LIANG Shanqing, ZHAO Guangjie, FU Feng. Diagnosis of internal defects of wood with stress wave tomography[J]. China Wood Industry, 2010, 24(5):11-13.

[6] 王立海，徐華東,閆在興,等. 傳感器的數量與分布對應力波檢測原木缺陷效果的影響[J]. 林業科學, 2008, 44(5):115-121.

WANG Lihai, XU Huadong, YAN Zaixing, et al. Effects of sensor quantity and planar distribution on testing results of log defects based on stress wave[J]. Scientia Silvae Sinicae, 2008, 44(5):115-121.

[7] 余觀夏，張愛珍,史伯章,等. 用應力波頻譜分析技術檢測原木中的腐朽[J].東北林業大學學報,2007,35(10):20-25.

YU Guanxia, ZHANG Aizhen, SHI Bozhang, et al. Detection of timber decay by stress wave frequency spectrum[J]. Journal of Northeast Forestry University, 2007, 35(10):20-25.

[8] 王靖濤.樁基礎設計與檢測[M].武漢:華中科技大學出版社, 2005.

[9] 楊學春，王立海. 木材應力波無損檢測研究[M].北京:科學出版社, 2011.

[10] WANG X，ROSS R J，BRASHAW B K，et al. Diameter effect on stress-wave evaluation of modulus of elasticity of small-diameter logs[J]. Wood and Fiber Science，2004，36(3)：368-377.

[11] WANG X. Acoustic measurements on trees and logs：a review and analysis[J]. Wood Science and Technology，2013，47(5)：965-975.

[12] SANSALONE M, STREETT W B. Impact echo: nondestructive evaluation of concrete and masonry[M]. Ithaca, NY: Bullbrier Press, 1997.

[13] ZHAO X, PATEL T H, ZUO M J. Multivariate EMD and full spectrum based condition monitoring for rotating machinery[J]. Mechanical Systems and Signal Processing, 2012, 27: 712-728.

[14] SHEN Chenxing, LI Zhixiong, QIN Li, et al. Recent progress on mechanical condition monitoring and fault diagnosis[J]. Procedia Engineering, 2011, 15: 142-146.

[15] ZHANG J, YAN R, GAO R X, et al. Performance enhancement of ensemble empirical mode decomposition[J]. Mech Syst Signal Process, 2010,24:2104-2123.

[16] WU Z, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Adv Adaptive Data Anal, 2008, 1(1):1-41.

[17] GUO W, TSE P W. Enhancing the ability of ensemble empirical mode decomposition in machine fault diagnosis[C]∥ Prognostics and Health Management Conference. IEEE, 2010.

[18] SCHEFFLER M，NIEMZ P，HARDTKE H J. Numerical simulation of sound propagation in wood in presence of defects[J]. Holz als Roh und Werkstoff,2002,60(5)：397-404.

[20] FENG Hailin, FANG Yiming, LI Jian, et al. Detecting Longitudinal of Internal Log Hole Using an Impact-Echo method[J]. Bio Resources,2015, 10(4): 7569-7579.

[21] GIBSON A, POPOVICS J S. Lamb wave basis for impact-echo method analysis[J]. Eng Mech, 2005,131(4):438-443.

[22] CARINO N J. The impact-echo method：an overview[C]∥Proceedings of the 2001 Structures Congress and Exposition. Washington DC：American Society Civil Engineers，2001.