基于頻響函數(shù)法的固定結(jié)合部參數(shù)辨識研究

田豐慶， 朱堅民， 李孝茹， 李 堯(上海理工大學(xué) 機械工程學(xué)院，上海 200093)

機械結(jié)構(gòu)中存在著大量的固定連接，如栓接、鉚接、焊接、粘接等，固定結(jié)合部的存在增加了整體結(jié)構(gòu)的阻尼，減小了整體結(jié)構(gòu)的剛度，使整體結(jié)構(gòu)的動態(tài)特性變差。因此準確地辨識結(jié)合部參數(shù)對確定整體結(jié)構(gòu)的動態(tài)特性具有重要意義。

固定結(jié)合部等效參數(shù)的辨識方法主要有模態(tài)分析法與頻響函數(shù)法[1]。模態(tài)分析法的基本思想是將機械結(jié)構(gòu)的動力學(xué)方程變換到模態(tài)坐標空間，并截去部分高階模態(tài)后確定結(jié)合部的數(shù)學(xué)模型[2]。該方法的特點是需要準確確定整體結(jié)構(gòu)的模態(tài)參數(shù)，對于整體結(jié)構(gòu)模態(tài)相對密集的對象難以應(yīng)用。頻響函數(shù)法的基本思想是根據(jù)機械結(jié)構(gòu)中子結(jié)構(gòu)之間的連接關(guān)系，耦合各子結(jié)構(gòu)的頻響函數(shù)確定整體結(jié)構(gòu)的頻響函數(shù)，再對結(jié)合部參數(shù)進行辨識。頻響函數(shù)法原理簡單、實驗方便、應(yīng)用廣泛。

針對上述問題，本文以螺栓連接的兩個金屬梁的栓接結(jié)合部為例進行研究，采用頻響函數(shù)法建立其動力學(xué)模型，提出對結(jié)合部中各參數(shù)項單獨靈敏度分析、單獨辨識的方法。通過仿真與實驗算例驗證該方法的正確性。

1 基本原理

1.1 頻響函數(shù)法辨識固定結(jié)合部參數(shù)的基本原理

機械結(jié)構(gòu)通常可以拆分為子結(jié)構(gòu)與連接子結(jié)構(gòu)的結(jié)合部，如圖1所示，整體結(jié)構(gòu)W拆分為子結(jié)構(gòu)A、B和結(jié)合部J。其中e1、e2表示結(jié)合部部分，a、b表示結(jié)合部以外部分。根據(jù)子結(jié)構(gòu)A、子結(jié)構(gòu)B以及整體結(jié)構(gòu)W頻響函數(shù)的定義，可得位移與外力的關(guān)系式，如式(1)～(3)所示。式中X表示結(jié)構(gòu)的位移矢量，F(xiàn)表示結(jié)構(gòu)的力矢量，H表示頻響函數(shù)。下標A、B表示對應(yīng)的子結(jié)構(gòu)，W表示整體結(jié)構(gòu)。下標a、b、e1、e2表示頻響函數(shù)對應(yīng)的激勵點、響應(yīng)點，如Hae1表示在e1點激勵 a點響應(yīng)的頻響函數(shù)。上標有*代表此項參數(shù)為整體結(jié)構(gòu)的參數(shù)，上標無*代表此項參數(shù)為子結(jié)構(gòu)的參數(shù)。

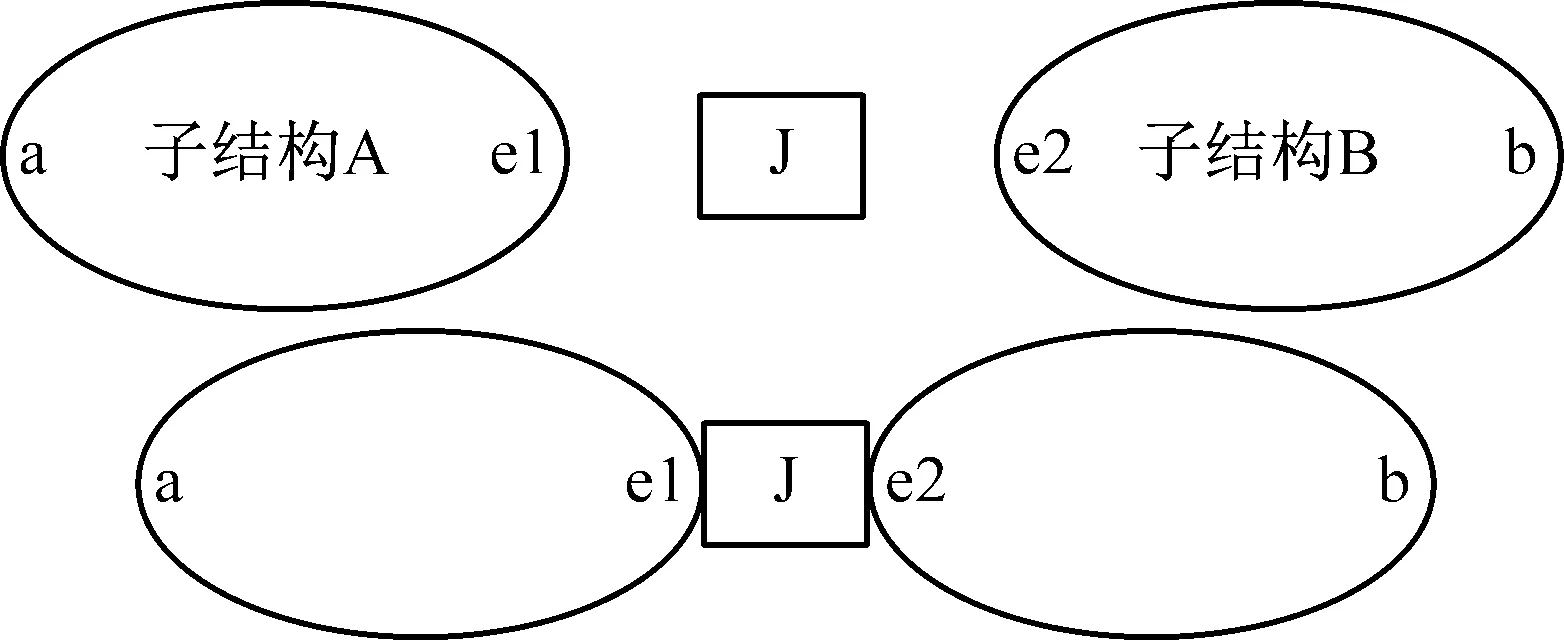
圖1 子結(jié)構(gòu)與整體結(jié)構(gòu)關(guān)系示意圖Fig.1 Relationship between substructure and assembly structure

(1)

(2)

(3)

假設(shè)結(jié)合部不受外力，則結(jié)合部之間的力為作用力與反作用力，如式(4)所示。由于結(jié)合部的頻響函數(shù)HJ與等效阻抗ZJ互逆，可得式(5)。忽略結(jié)合部的質(zhì)量，結(jié)合部的動力學(xué)公式可以表示為式(6)

Fe1=-Fe2

(4)

(5)

Xe2-Xe1=HJFe1

(6)

聯(lián)合式(1)～(6)，可得整體結(jié)構(gòu)的原點、跨點頻響函數(shù)如式(7)～(10)所示

(7)

(8)

(9)

(10)

由式(7)～(10)可以推導(dǎo)出相應(yīng)的4個結(jié)合部參數(shù)的辨識公式，如式(11)～式(14)。這4個辨識公式分為兩組，式(11)與式(14)為第一組，式(12)與式(13)為第二組。第一組的兩個公式都采用整體結(jié)構(gòu)的原點頻響函數(shù)作參數(shù)，只是對應(yīng)整體結(jié)構(gòu)的原點不同。因此將第一組的兩個公式等效為一個辨識公式如式(11)。第二組與第一組情況相似，不同的是第二組公式采用了整體結(jié)構(gòu)的跨點頻響函數(shù)，可將第二組公式等效為式(12)所示的辨識公式

(11)

(12)

(13)

(14)

根據(jù)上述公式辨識結(jié)合部參數(shù)需要先求取公式中的頻響函數(shù)。以式(11)中的頻響函數(shù)He1a為例說明，如果a、e1兩節(jié)點都只有一個自由度，則He1a意義明確，代表一個頻響函數(shù)。如果a、e1兩節(jié)點都有兩個自由度，如歐拉梁模型，則He1a代表4個頻響函數(shù)組成的頻響函數(shù)矩陣。分別為平移振動的頻響函數(shù)(平動頻響函數(shù))、扭轉(zhuǎn)振動的頻響函數(shù)(轉(zhuǎn)動頻響函數(shù))、平移與扭轉(zhuǎn)振動耦合的頻響函數(shù)(耦合頻響函數(shù))。

對子結(jié)構(gòu)而言，根據(jù)有限元理論建立子結(jié)構(gòu)的有限元模型，可以計算其所有頻響函數(shù)(包括平動、轉(zhuǎn)動及耦合頻響函數(shù))。對整體結(jié)構(gòu)而言，由于結(jié)合部參數(shù)未知，無法構(gòu)建整體結(jié)構(gòu)的有限元模型，需用實驗方法得到所有頻響函數(shù)。其中平動頻響函數(shù)可以通過實驗測得，但轉(zhuǎn)動與耦合頻響函數(shù)需專門的測量設(shè)備[17]。本文采用有限差分法[18]通過兩點分別激勵，并測量其響應(yīng)的平動頻響函數(shù)后再計算出其中一點的所有頻響函數(shù)。

1.2 有限差分法計算轉(zhuǎn)動頻響函數(shù)

以梁結(jié)構(gòu)為模型說明轉(zhuǎn)動頻響函數(shù)的求法，計算如圖2中B點激勵B點響應(yīng)的所有頻響函數(shù)。在B點附近設(shè)置A點，分別激勵A(yù)點、B點，并且在A點、B點測試響應(yīng)信號，可得平動頻響函數(shù)HAA_tt、HAB_tt、HBA_tt、HBB_tt，組成矩陣如式(15)，其中字母tt表示平動頻響函數(shù)。

設(shè)A、B兩點之間的距離為s，確定前向差分公式如式(16)所示。由式(17)可以計算出B點激勵B點響應(yīng)的所有頻響函數(shù)。字母rr表示轉(zhuǎn)動頻響函數(shù)，字母tr、rt表示耦合頻響函數(shù)。

圖2 有限差分法求B點頻響函數(shù)Fig.2 Finite difference method for FRFs of point B

(15)

(16)

(17)

1.3 結(jié)合部參數(shù)單獨辨識原理

由辨識公式(11)、(12)可知，如果辨識公式中子結(jié)構(gòu)和整體結(jié)構(gòu)的頻響函數(shù)可以確定，則結(jié)合部的參數(shù)可以通過兩個辨識公式中任意一個計算得到。從理論上講，對應(yīng)于每個頻率都可計算出一組結(jié)合部參數(shù)，并且計算結(jié)果應(yīng)該相等。但事實并非如此，計算的結(jié)果不相同甚至部分結(jié)果相差較大。如何找出相對誤差較小的結(jié)合部參數(shù)所對應(yīng)的辨識頻段是準確辨識結(jié)合部參數(shù)的關(guān)鍵。

本文方法的主要思路是：通過僅改變結(jié)合部參數(shù)中某一項參數(shù)的大小得到幾組新參數(shù)，如以2倍、1倍與0.5倍參數(shù)為例的三組參數(shù)。用該三組參數(shù)模擬結(jié)合部對整體結(jié)構(gòu)進行模態(tài)分析，對比三組參數(shù)分析得出的固有頻率值，得到該參數(shù)由0.5倍變至2倍時引起的每一階固有頻率的相對變化量，用相對誤差表示，相對誤差越大，表示該參數(shù)對此階固有頻率值的影響越大，則該參數(shù)在此階固有頻率處的靈敏度越高。根據(jù)李玲等的研究，在靈敏度高的頻段可以準確地辨識出結(jié)合部參數(shù)。本文采用上述方法確定某一結(jié)合部參數(shù)的靈敏模態(tài)，并在該模態(tài)處辨識參數(shù)，并依此方法辨識出所有的結(jié)合部參數(shù)。

2 仿真算例研究

2.1 集中質(zhì)量模型

集中質(zhì)量法在機械結(jié)構(gòu)結(jié)合部參數(shù)建模中應(yīng)用廣泛，在集中質(zhì)量模型中結(jié)合部多數(shù)采用線性彈簧阻尼單元模擬。本文首先以集中質(zhì)量模型為例進行研究，構(gòu)建集中質(zhì)量模型如圖3所示，整體結(jié)構(gòu)W拆分為子結(jié)構(gòu)A、子結(jié)構(gòu)B及結(jié)合部J。結(jié)合部采用一組彈簧阻尼單元模擬，用ZJ表示結(jié)合部等效阻抗，kJ和cJ分別表示結(jié)合部的剛度和阻尼，建立其等效模型,如式(18)所示。

Model 1ZJ=kJ+iwcJ

(18)

圖3 集中質(zhì)量模型Fig.3 Lumped mass model

集中質(zhì)量模型中的參數(shù)如表1所示。利用有限元理論可計算子結(jié)構(gòu)A、B的頻響函數(shù)。

構(gòu)建整體結(jié)構(gòu)的有限元模型，可求得整體結(jié)構(gòu)前4階的固有頻率分別為228 Hz、449 Hz、781 Hz、853 Hz。

根據(jù)1.3節(jié)的分析，用3組kJ的不同倍數(shù)的結(jié)合部參數(shù)kJ+iwcJ、2×kJ+iwcJ及0.5×kJ+iwcJ分別模擬結(jié)合部并進行模態(tài)分析，將計算出的3條頻響函數(shù)曲線繪制在圖5中，同時將對應(yīng)的整體結(jié)構(gòu)固有頻率值列于表2。對每一階模態(tài)，用0.5kJ與2kJ作為結(jié)合部參數(shù)對應(yīng)的固有頻率的差值除以kJ作為結(jié)合部參數(shù)對應(yīng)的固有頻率值，得此kJ由0.5倍～2倍的變化量下所引起的這一階固有頻率值的變化率，用相對誤差表示，見表2。

表1 集中質(zhì)量模型參數(shù)表Tab.1 Parameters of the lumped mass model

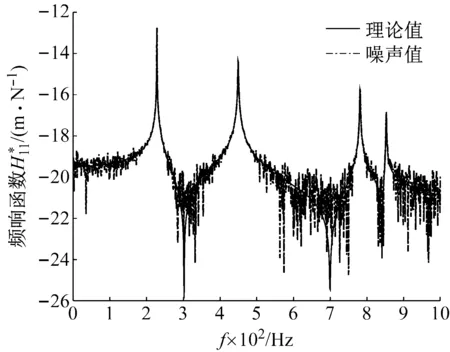
圖4 頻響函數(shù)的理論值與噪聲值Fig.4 Theoretical and noisy value of

表2 kJ靈敏度分析表Tab.2 Sensitivity analysis of kJ

圖5 對kJ靈敏度分析Fig.5 Sensitivity analysis of kJ

由表2和圖5可知，剛度kJ在整體結(jié)構(gòu)前4階模態(tài)處的靈敏度不相同。在第1階、第3階模態(tài)處，不同倍數(shù)的kJ對應(yīng)的固有頻率值變化較小，在這兩階模態(tài)處不靈敏。在第2階、第4階模態(tài)處，從圖5看出固有頻率值有較大變化，由相對誤差的數(shù)值分析可知，kJ的大小變化在第2階模態(tài)引起的誤差最大，達到10.2%，因此剛度kJ在整體結(jié)構(gòu)的第2階模態(tài)處靈敏度最高。則本算例中剛度kJ在第2階固有頻率(449 Hz)處辨識。

圖6為根據(jù)式(11)辨識的kJ值，由圖6可知在每個頻率處所計算出的結(jié)合部參數(shù)值并不相等，有些與理論值之間還有較大的誤差，但在參數(shù)kJ最靈敏的模態(tài)頻率(449 Hz)附近，計算值與理論值比較接近。圖7表示的是結(jié)合部阻尼參數(shù)cJ的辨識情況，其辨識方法與剛度參數(shù)的辨識方法相同。

采用式(12)辨識參數(shù)的方法與式(11)的辨識方法相同，兩者的辨識結(jié)果列于表3。

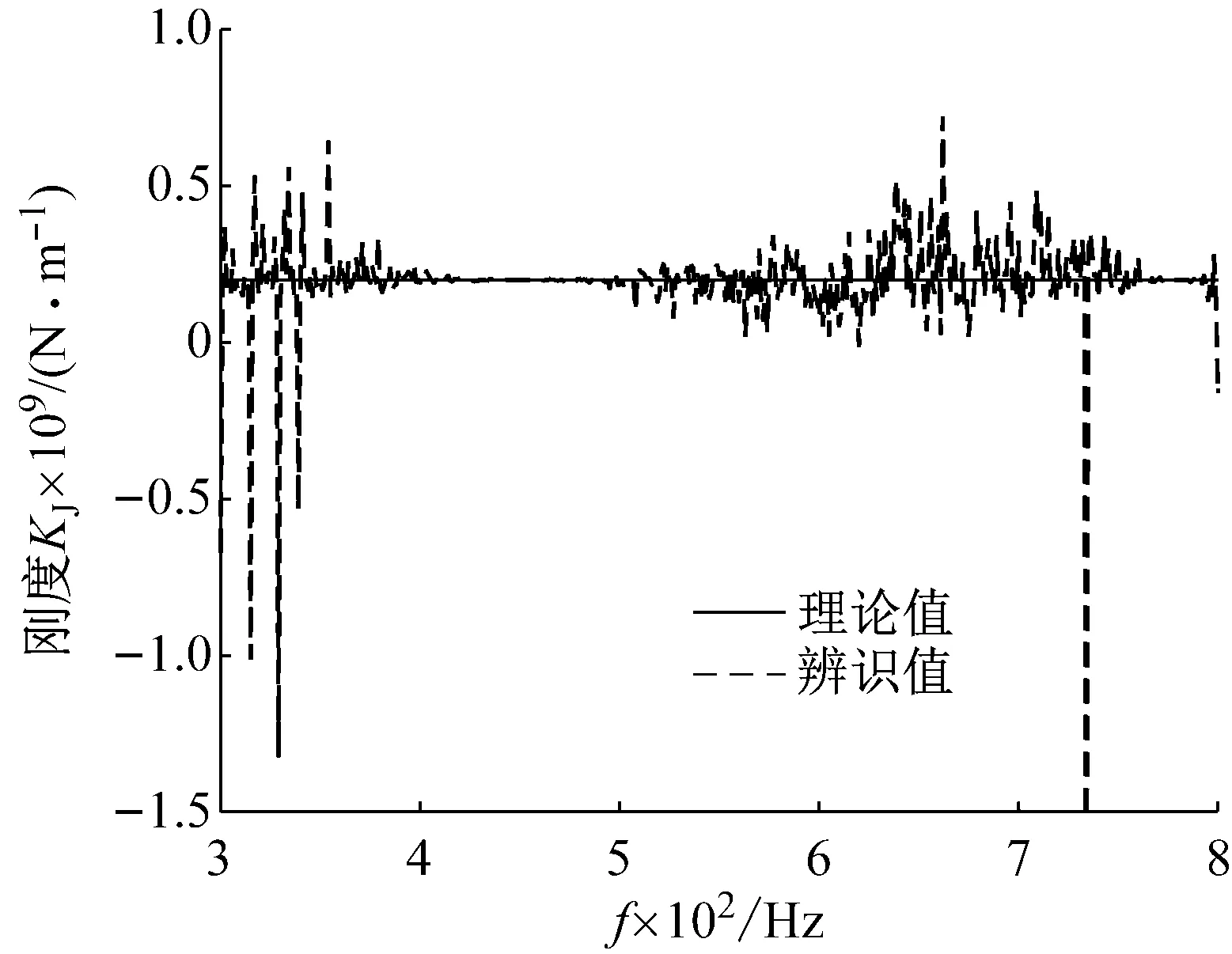
圖6 式(11)的計算出的kJ值Fig.6 The values of kJ calculated by formula (11)

圖7 式(11)計算出的cJ值Fig.7 The values of cJ calculated by formula (11)

由表3可知，式(11)和式(12)的辨識結(jié)果差異較小,式(11)的辨識精度略高。這主要是由于辨識公式(11)中采用整體結(jié)構(gòu)的原點頻響函數(shù)作為參數(shù)，辨識公式(12)中采用整體結(jié)構(gòu)的跨點頻響函數(shù)作為參數(shù)。對比這兩種頻響函數(shù)，原點頻響函數(shù)的精度比跨點頻響函數(shù)略高，這與文獻[14]的結(jié)論一致。

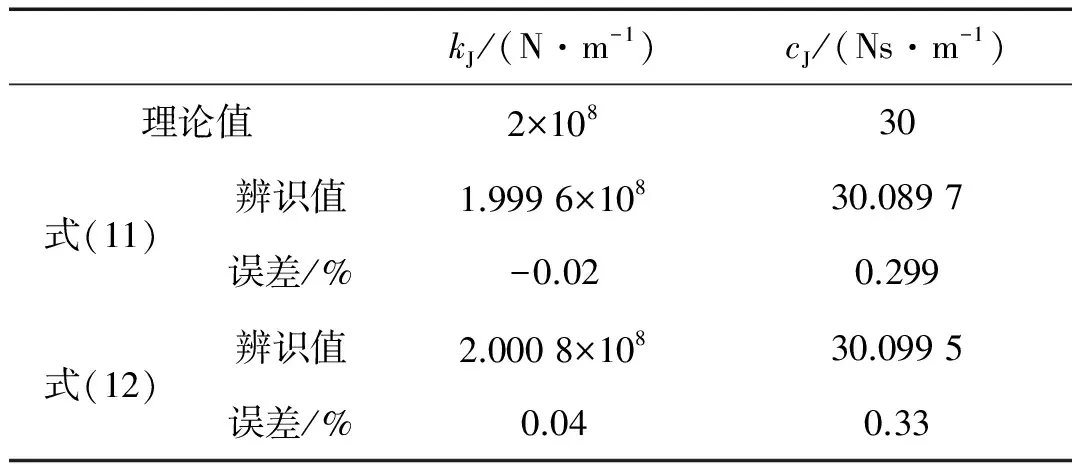
表3 集中質(zhì)量模型結(jié)合部參數(shù)辨識結(jié)果Tabl.3 Parameter identification result of thejoint in lumped mass model

當結(jié)合部等效為單自由度彈簧阻尼單元時，式(11)和式(12)的辨識結(jié)果差異較小，具體應(yīng)用時可根據(jù)實際情況中容易獲得的頻響函數(shù)選擇合適的辨識公式。

2.2 歐拉梁模型

如圖8所示的兩個子結(jié)構(gòu)是兩端自由的歐拉梁，e1與e2固定連接組成整體結(jié)構(gòu)。結(jié)合部采用2節(jié)點4自由度的剛度矩陣模擬,建立結(jié)合部的等效模型如式(19)所示。式中ZJ表示結(jié)合部等效阻抗，ktt表示平動剛度，krr表示轉(zhuǎn)動剛度，ktr和krt示耦合剛度，c表示對應(yīng)的阻尼，w表示角頻率。則辨識公式(11)、(12)中的頻響函數(shù)為平動、轉(zhuǎn)動、耦合頻響函數(shù)組成的矩陣。

(19)

圖8 歐拉梁模型Fig.8 Euler-Bernoulli beam model

梁的彈性模量為1.97×1011Pa，密度為7 865 kg/m3，根據(jù)有限元理論可計算出子結(jié)構(gòu)A、B的所有頻響函數(shù)。

基于表4中的結(jié)合部參數(shù)，建立整體結(jié)構(gòu)的有限元模型，其中耦合參數(shù)ktr和krt相等，ctr和crt相等。可得整體結(jié)構(gòu)在0～1 000 Hz以內(nèi)有四階固有頻率，分別為87 Hz、249 Hz、466 Hz、794 Hz。采用前述靈敏度分析方法，對結(jié)合部參數(shù)ktt、krt(ktr)和krr分別進行靈敏度分析，分析結(jié)果如圖9～11所示。

由圖9可知，平動剛度ktt在整體結(jié)構(gòu)第1、2、3階模態(tài)處不靈敏，在第4階模態(tài)處最靈敏；由圖11可知，轉(zhuǎn)動剛度krr在整體結(jié)構(gòu)第1、2、4階模態(tài)處不靈敏，在第3階模態(tài)處最靈敏；由圖10可知耦合剛度ktr在所考慮的頻段都不靈敏。

圖9 對ktt的靈敏度分析Fig.9 Sensitivity analysis of ktt

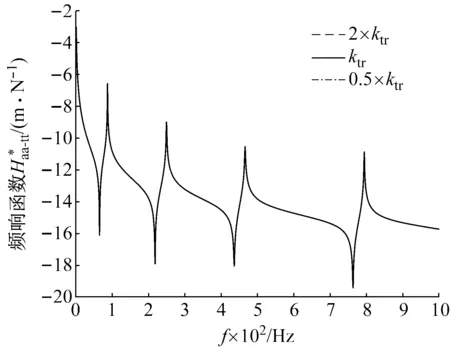
圖10 對ktr的靈敏度分析Fig.10 Sensitivity analysis of ktr

圖11 對krr的靈敏度分析Fig.11 Sensitivity analysis of krr

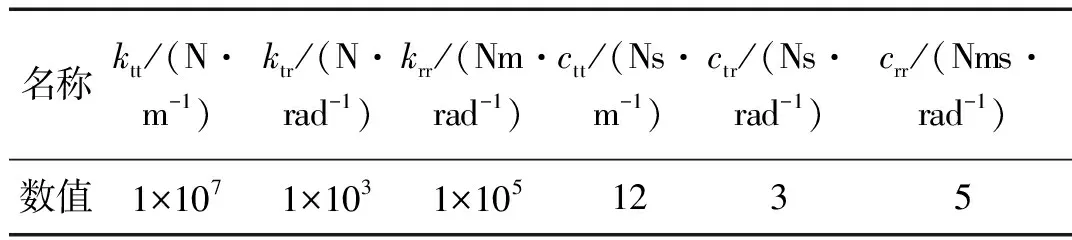
表4 結(jié)合部參數(shù)表Tab.4 Parameters of the joint

圖12 式(11)計算出的ktt值Fig.12 ktt calculated by formula (11)

圖13 式(11)計算出的ktr值Fig.13 ktr calculated by formula (11)

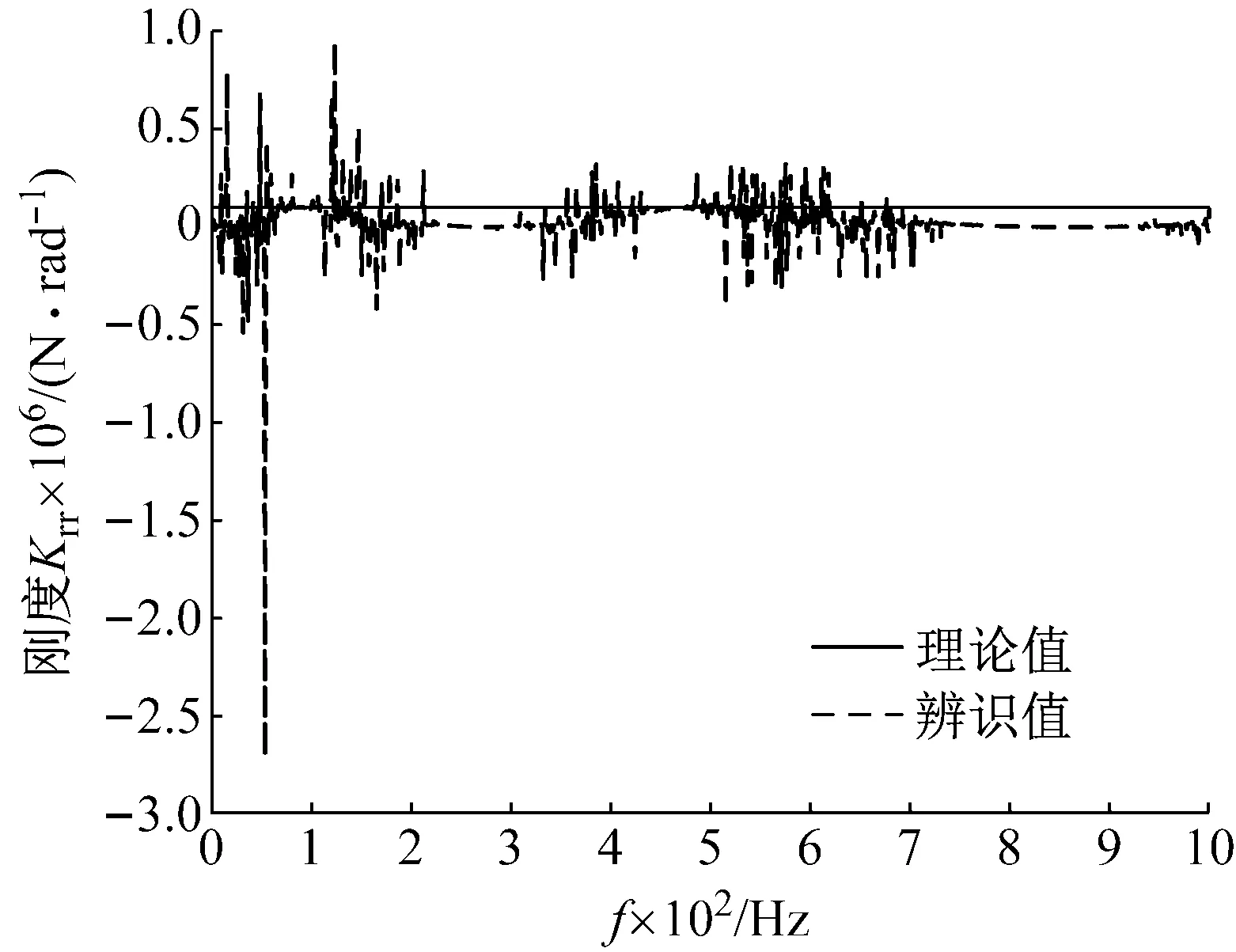
圖14 式(11)計算出的krr值Fig.14 krr calculated by formula (11)

由表5可知，與集中質(zhì)量模型的算例結(jié)果類似，采用式(11)辨識結(jié)果的誤差比式(12)的誤差小。

耦合參數(shù)在整體結(jié)構(gòu)的所考慮的頻段都不靈敏，即耦合參數(shù)的大小變化對整體結(jié)構(gòu)的動態(tài)特性影響較小，具體辨識過程中很難準確辨識。表5中耦合參數(shù)的誤差較大也印證了這一點。對于此類情況，可忽略結(jié)合部的耦合參數(shù)，直接構(gòu)建結(jié)合部等效模型如式(20)所示

表5 辨識公式的結(jié)果Tab.5 Parameter identification result

(20)

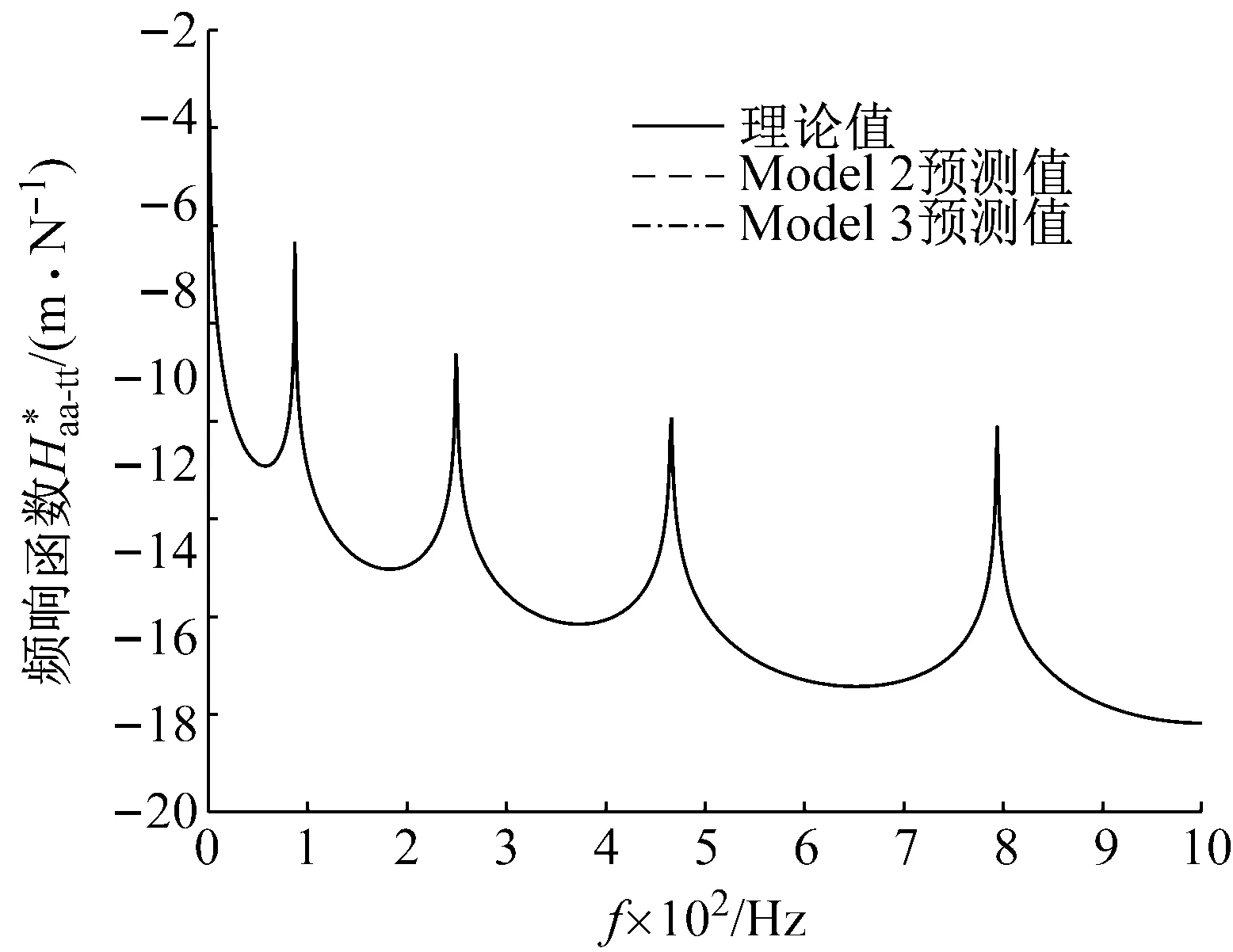
圖15 整體結(jié)構(gòu)頻響函數(shù)的預(yù)測值與理論值對比圖Fig.15 Comparison between the predicted values and the theoretical values of assembly structure FRFs

3 實驗算例研究

圖17為實驗時測試點分布的具體位置及子結(jié)構(gòu)單元劃分圖。兩個子結(jié)構(gòu)的材料為Q235，通過e1、e2點連接。子結(jié)構(gòu)A的長度為400 mm，子結(jié)構(gòu)B的長度300 mm，梁結(jié)構(gòu)的截面寬為30 mm、高為10 mm，a、b、e1、e2為具體的激勵點與響應(yīng)點。

采用Model 3模擬整體結(jié)構(gòu)的結(jié)合部，選取辨識式(11)辨識結(jié)合部參數(shù)。

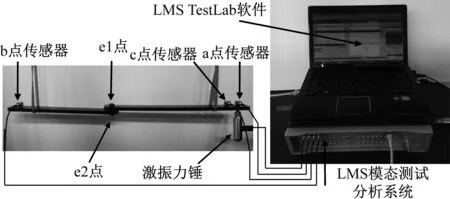
圖16 實驗原理Fig.16 Experimental principle

圖17 實驗測試點分布圖Fig.17 Testing location distribution

3.1 計算子結(jié)構(gòu)頻響函數(shù)

實驗材料的密度為7 803 kg/m3，彈性模量為1.95×1011Pa。建立子結(jié)構(gòu)A和子結(jié)構(gòu)B的有限元模型，子結(jié)構(gòu)A劃分為15個單元，子結(jié)構(gòu)B劃分為14個單元，計算出辨識公式(11)中子結(jié)構(gòu)A與子結(jié)構(gòu)B的所有頻響函數(shù)。

3.2 計算整體結(jié)構(gòu)a點的頻響函數(shù)

在a點附近設(shè)置c點，a點距離子結(jié)構(gòu)A的端部為30 mm，a、c兩點之間的距離為s=30 mm。

分別激勵a點、c點，讀取a點、c點的響應(yīng)，得相應(yīng)的平動頻響函數(shù)曲線，如圖18所示。由式(17)計算得整體結(jié)構(gòu)a點激勵a點響應(yīng)的所有頻響函數(shù)，表示在圖19中。同時可得在0～1 000 Hz以內(nèi)整體結(jié)構(gòu)有4階固有頻率，分別為92 Hz、300 Hz、564 Hz、900 Hz。

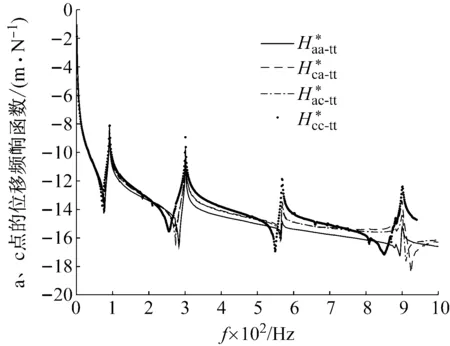
圖18 實驗測試a點、c點的頻響函數(shù)Fig.18 Experimental FRFs result of location a and c

圖19 整體結(jié)構(gòu)a點的頻響函數(shù)Fig.19 FRFs result of point a to assembly structure

3.3 靈敏度分析

電化學(xué)問題離不開電子的行為，說它是電化學(xué)理論的靈魂并不過分，電子的行為表現(xiàn)為定向和定量兩個方面。定向方面列表如下：而定量方面可對原電池及電解池的相關(guān)問題進行全面的計算。

表6 遺傳算法尋優(yōu)結(jié)果Tab.6 Optimization result of GA

3.4 結(jié)合部參數(shù)的辨識

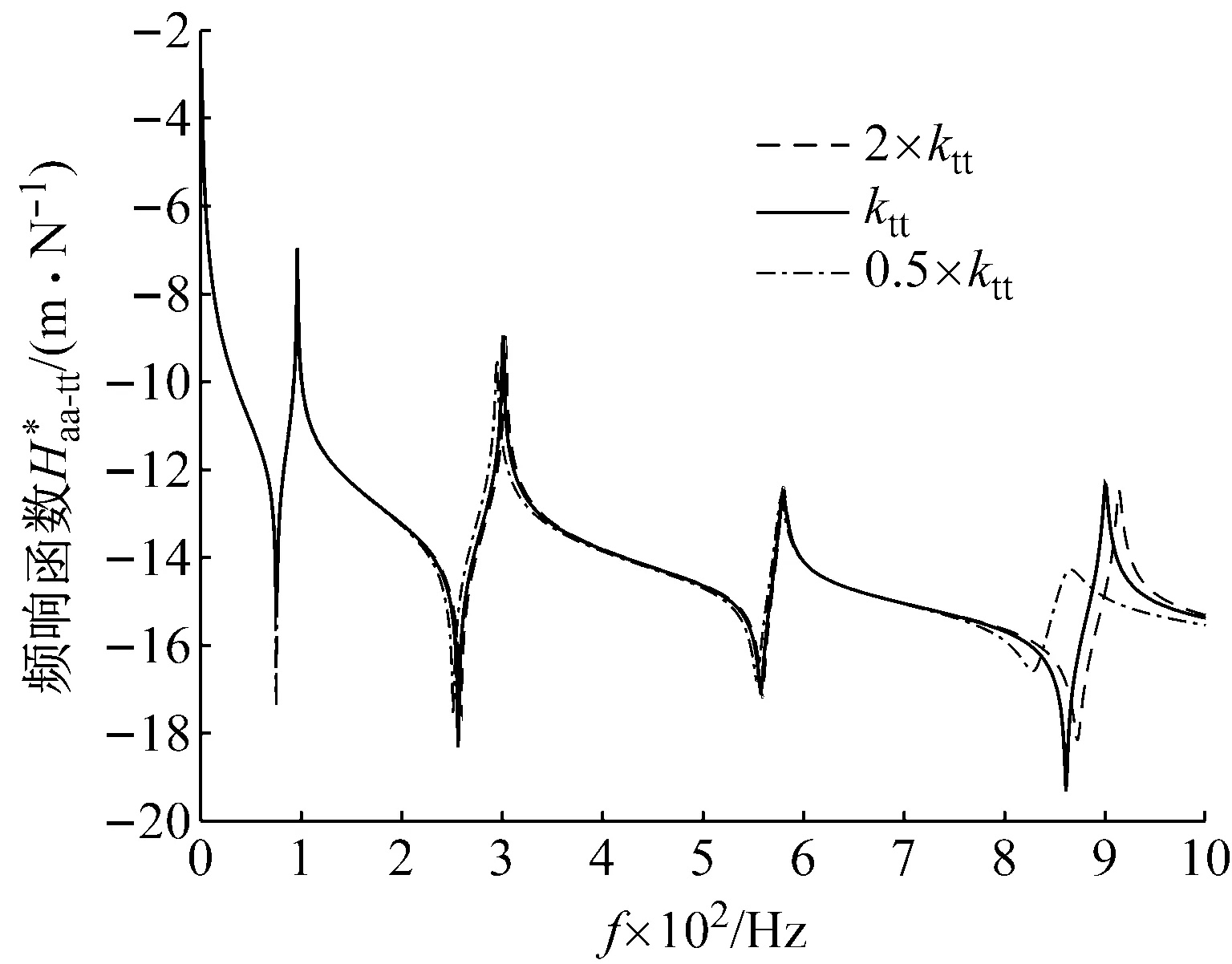
圖20 對ktt靈敏度分析Fig.20 Sensitivity analysis of ktt

圖21 對krr靈敏度分析Fig.21 Sensitivity analysis of krr

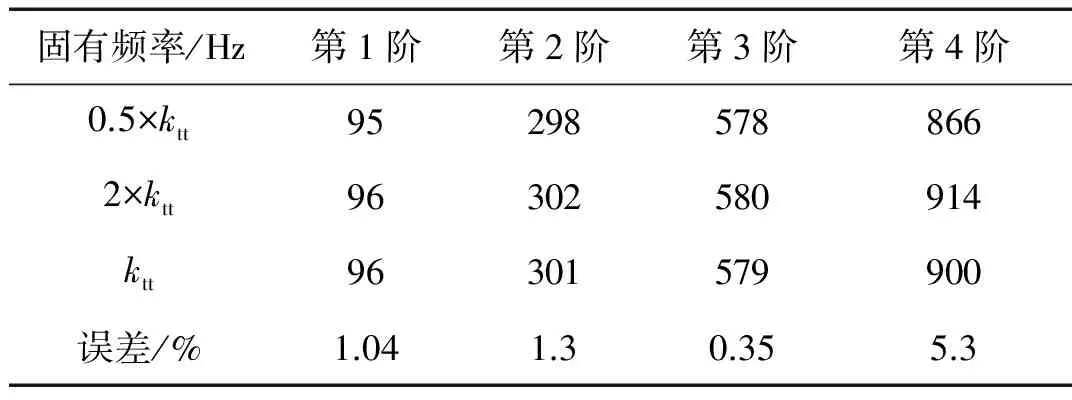
表7 ktt靈敏度分析表Tab.7 Sensitivity analysis of ktt

圖22 整體結(jié)構(gòu)的頻響函數(shù)Fig.22 FRFs of assembly structure

表10 遺傳算法與本文方法的辨識結(jié)果對比Tab.10 Identification result comparison betweenGA and the proposed method

4 結(jié) 論

(1)提出一種對結(jié)合部參數(shù)辨識的新方法。先通過遺傳算法尋優(yōu)確定結(jié)合部參數(shù)的初值，再對結(jié)合部各項參數(shù)進行單獨靈敏度分析，計算該參數(shù)在每一階模態(tài)處的靈敏度，在最靈敏的模態(tài)處單獨辨識該項參數(shù)，最后依此方法辨識所有的結(jié)合部參數(shù)。

(2)仿真和實驗算例的研究結(jié)果表明，基于本文方法辨識的結(jié)合部參數(shù)所預(yù)測的整體結(jié)構(gòu)頻響函數(shù)與實驗測試的頻響函數(shù)具有較高的一致性，從兩者的固有頻率的對比結(jié)果看，最大的相對誤差出現(xiàn)在第1階，為1.09%，參數(shù)辨識精度較高。

參 考 文 獻

[1] 蔡力鋼,王鋒,李玲，等.栓接結(jié)合部動態(tài)特性研究進展[J].機械工程學(xué)報,2013,49(9):158-168.

CAI Ligang, WANG Feng, LI Ling, et al. Review on dynamic properties of bolted joints[J]. Journal of Mechanical Engineering, 2013, 49(9):158-168.

[2] 李金峰,王立平.改進的受力狀態(tài)映射法在結(jié)合部動力學(xué)參數(shù)辨識中應(yīng)用[J].振動與沖擊,2016,35(6):488-496.

LI Jinfeng,WANG Liping. Application of an improved force-state mapping method in dynamic parameter identification of joints[J]. Journal of Vibration and Shock, 2016, 35(6):488-496.

[3] OKUBO N, MIYAZAKI M. Development of uncoupling technique and its application[C]//Proceedings of International Modal Analysis Conference. Orlando, FL，1984.

[4] TSAI J S, CHOU Y F. The identification of dynamic characteristics of a single bolt joint[J]. Journal of Sound and Vibration, 1988, 125:487-502.

[5] WANG J H, LIOU C M. Experimental substructure synthesis with special consideration of joint effect[J]. International Journal of Analytical and Experimental Modal Analysis, 1989, 5(1):1-12.

[6] HWANG H Y. Identification techniques of structure connection parameters using frequency response functions[J]. Journal of Sound and Vibration, 1998, 212(3):469-479.

[9] REN Y, BEARDS C. F. Identification of joint properties of a structure using FRF data[J]. Journal of Sound and Vibration, 1995, 186(4):567-587.

[10] YANG T, FAN S H, LIN C S. Joint stiffness identification using FRF measurements[J]. Computers & Structures, 2003, 81: 2549-2556.

[11] MEHRPOUYA M, SANATI M, PARK S S. Identification of joint dynamics in 3D structures through the inverse receptance coupling method[J]. International Journal of Mechanical Sciences, 2016, 105: 135-145.

[12] 李玲,蔡安江,蔡力鋼，等.栓接結(jié)合部動態(tài)特性辨識方法[J].機械工程學(xué)報,2013,49(7):168-175.

LI Ling, CAI Anjiang, CAI Ligang, et al. Identification method for dynamic properties of bolted joints[J]. Journal of Mechanical Engineering, 2013, 49(7):168-175.

[13] 李玲,蔡力鋼,郭鐵能，等.機械結(jié)合部動態(tài)剛度辨識與實驗研究[J].振動工程學(xué)報,2012,25(5):488-496.

LI Ling, CAI Ligang, GUO Tieneng, et al. Identification and experimental research on dynamic stiffness of mechanical joints[J]. Journal of Vibration Engineering, 2012, 25(5):488-496.

[14] 郭鐵能,李玲,蔡力鋼，等.基于頻響函數(shù)辨識機械結(jié)合部動態(tài)參數(shù)的研究[J].振動與沖擊,2011,30(5):69-72．

GUO Tieneng, LI Ling, CAI Ligang, et a1. Identifying mechanical joint dynamic parameters based on measured frequency response functions[J]. Journal of Vibration and Shock, 201l, 30(5):69-72．

[15] 李玲,蔡安江,蔡力鋼，等.栓接結(jié)合部動態(tài)特性參數(shù)辨識新方法[J].振動與沖擊,2014,33(14):15-32.

LI Ling, CAI Anjiang, CAI Ligang, et al. New method to identify dynamic characteristics of bolted joints[J]. Journal of Vibration and Shock, 2014, 33(14):15-32.

[16] 董冠華,殷勤,殷國富，等.機床結(jié)合部動力學(xué)建模與辨識方法的研究[J].機械工程學(xué)報,2016,52(5):162-168.

DONG Guanhua, YIN Qin, YIN Guofu, et al. Research on dynamics modeling and identification of machine tool joints[J]. Journal of Mechanical Engineering, 2016, 52(5): 162-168.

[17] KLERK D, RIXEN D, VOORMEEREN S, et al. Solving the RDOF problem in experimental dynamic substructuring[C]//Proceedings of the 26th international Modal Analysis Conference. Orlando, FL, 2008.

[18] DUARTE M L M,EWINS D J. Rotational degrees of freedom for structural coupling analysis via finite difference technique with residual compensation[J]. Mechanical Systems and Signal Processing, 2000, 14(2):205-227.