輪軌黏著下計及齒輪嚙合特性的機車驅動系統主共振

王 燕， 劉建新， 李 淼， 李奕璠， 蔡久鳳(. 西南交通大學 機械工程學院， 成都 600; . 西南交通大學 牽引動力國家重點實驗室， 成都 600;. 中車株洲電力機車研究所有限公司， 湖南 株洲 400)

齒輪嚙合過程中，由于內部嚙合剛度和傳遞誤差的動態變化以及齒側間隙的存在，導致系統表現出強烈的非線性動力學特性。該特性得到了國內外學者的高度關注,并開展了大量的研究[1-6]。而齒輪作為機車驅動系統的關鍵部件之一，其動力學特性不僅影響著機車驅動系統的振動性能，也影響著機車的動力傳輸和走行部的運行安全[7]。但是，目前針對計及齒輪嚙合特性的機車驅動系統的振動研究工作仍較為少見。此外，機車服役過程中，由于輪軌黏著的獨特性，使得機車驅動系統的外部激勵具有一定的特殊性。

基于此，本文建立了輪軌黏著下計及齒輪嚙合靜傳遞誤差、時變嚙合剛度和齒側間隙在內的機車驅動系統的動力學模型及方程，采用多尺度法進行求解，獲得了系統在內部齒輪嚙合動態激勵和外部輪軌黏著力共同作用下的系統主共振的頻率響應方程。并開展了實例研究，分析了系統參數變化對主共振頻率響應曲線的影響，仿真了不同蠕滑率下輪軌黏著力的動態變化對機車驅動系統主共振響應的影響。可為輪軌黏著下計及齒輪嚙合特性的機車驅動系統主共振問題提供參考依據。

1 機車驅動系統的動力學分析模型

機車驅動系統的動力學分析模型如圖1所示：其中，符號Ii、Ri、θi、Ti分別為主動(i=1)、被動(i=2)齒輪端上的等效轉動慣量、基圓半徑、轉動角位移和施加的力矩；km(t)、cm分別為齒輪嚙合剛度與阻尼；b為齒側間隙的一半；e(t)為齒輪靜傳遞誤差。

1.1 動力學方程

根據圖1所示的動力學分析模型，建立相應的動力學方程

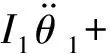
km(t)R1f(Δx)=T1，

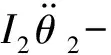
km(t)R2f(Δx)=-T2

(1)

式中：Δx=R1θ1-R2θ2-e(t)；f(Δx)為齒側間隙函數。

整理式(1)后得到

(2)

式中：me=I1I2/(I1R22+I2R12)；fm=I1R2R/(I1R22+I2R12)；F0=I2R1T1/(I1R22+I2R12)；R為車輪滾動圓半徑；Fu為輪軌黏著力。

式(2)包含了系統在力矩平衡狀態下的相對位移Δx0。因此，設靜平衡位置處的輪軌黏著力為Fu0，并令x=Δx-Δx0，整理式(2)后，得到

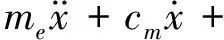
(3)

式中：靜平衡位置處的靜態載荷F1=F0+fmFu0。

1.2 齒輪嚙合的內部激勵

1.2.1 齒輪時變嚙合剛度

本文采用勢能原理求解齒輪時變嚙合剛度，因此，先將齒輪時變嚙合剛度表示為關于主動齒輪轉動角度θ1(單位°)的傅里葉級數的形式

(4)

式中:k0為平均嚙合剛度；kj為各階諧波項的幅值；φj為相位角；wn=2π/T，T=360/Z1，Z1為主動齒輪齒數。

進而通過變換得到km(t)關于時間的傅里葉級數形式

(5)

式中:we=2πZ1n1/60，n1為主動齒輪轉速,r/min。

1.2.2 齒輪靜傳遞誤差

齒輪靜傳遞誤差e(t)采用余弦函數表示為[8]

e(t)=e0+ercos(wet+φ)

(6)

式中:e0、er分別為齒輪靜傳遞誤差的常數項和諧波項的幅值；φ為相位角。

1.2.3 齒側間隙

選定齒側間隙的一半b為特征尺寸，將齒側間隙函數f(Δx)采用3次多項式表示為

f(Δx)/b=a1(Δx/b)+a3(Δx/b)3

(7)

式中:a1=0.167;a3=0.064。

1.3 輪軌黏著力

采用文獻[9]中簡化的輪軌黏著特性曲線，如圖2所示。

圖2中，um為最大黏著系數，sm為最大黏著系數對應的蠕滑率；ku為黏著特性曲線在AB段的斜率。OA段時，黏著系數處于黏著段；AB段時，黏著系數處于滑動段。

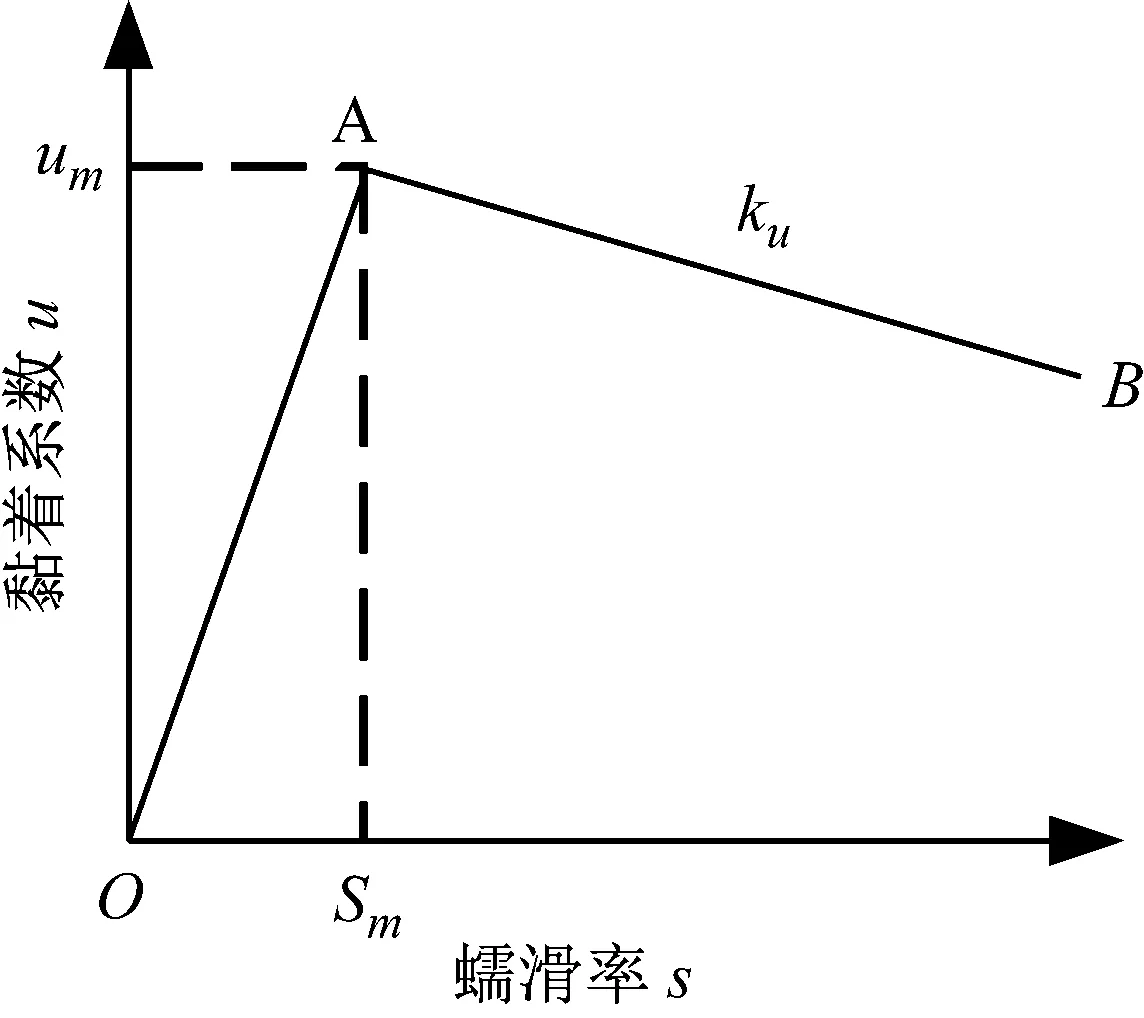
圖2 簡化的輪軌黏著特性曲線Fig.2 Simplified characteristic curve of wheel-rail adhesion

輪軌黏著系數u可表示為

(8)

式中:蠕滑率s是與輪對縱向速度v有關的函數，用圖1中的符號可表示為

(9)

參考文獻[10]中的處理方法，將蠕滑率進行泰勒級數展開，取其一次項后表示為

(10)

式中：w為平衡狀態下被動齒輪的轉動角速度；靜平衡位置處的蠕滑率s0=1-v/(wR)。

輪軌黏著力Fu=uQ，其中Q為軸重(單位：N)。輪軌黏著力的動態變化值Fu-Fu0可表示為

1) 靜平衡位置處的蠕滑率s0在OA段時

(11)

2) 靜平衡位置處的蠕滑率s0在AB段時

(12)

2 方程的無量綱化

將式(11)、式(12)代入式(3)，整理好后得到

(13)

式中：c1，F2，F3的值如表1所示。其中，c1為輪軌黏著力變化引起的等效阻尼；F2為靜態載荷的波動值；F3為誤差速度項激勵的系數。

表1 c1、F2、F3的值Tab.1 The values of c1、F2、F3

令x=by，Δx0=bΔy0(b為特征尺寸)，將式(5)～式(7)代入式(13)，整理后得到無量綱化后的方程為

a3(y+Δy0)3]=f1+f2+f3?sin(?τ+φ)+

f4?2cos(?τ+φ)

(14)

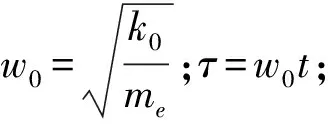
3 系統主共振的頻響方程

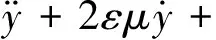
cos(?τ+φ-θ)

(15)

令ti=εiτ(i=0,1)，按照多尺度法[11-12]，設式(15)的近似解為

y=y0(t0,t1)+εy1(t0,t1)

(16)

將式(16)代入式(15)，令等式兩端ε0和ε1的系數分別相等，得到

(17)

ε1次

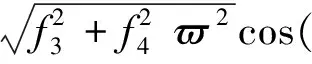
(18)

式(17)的解為

(19)

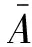
將式(19)代入式(18)，整理可得：

(20)

式中：cc為前面各項的共軛復數。

當?≈w1時，系統產生主共振。引入一個解諧參數σ=O(1)來表示激勵頻率?與系統固有頻率w1的接近程度。令?=w1+εσ，消除式(20)中的久期項后得到

(21)

設A=a(t1)eiβ(t1)/2并代入式(21)，當ke2與ke1相比較小時，分離實部與虛部，整理后得到

φ-θ)

(22a)

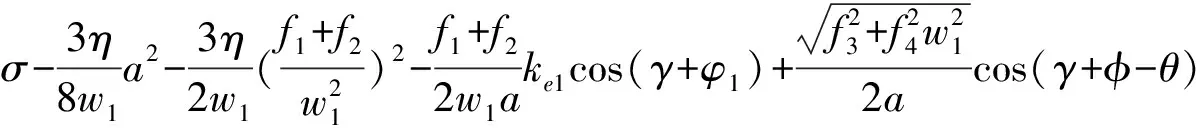
(22b)

式中：γ=σt1-β。

當a′=γ′=0時，系統存在穩態運動。由式(22)可得到穩態響應的頻率響應方程為

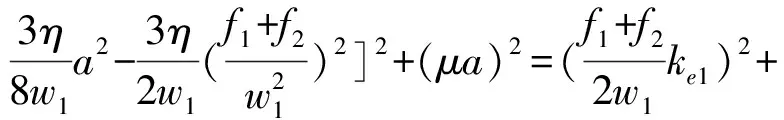
(23)

4 仿真分析

在某型機車驅動系統中，齒輪副的主要計算參數為：主動齒輪齒數Z1=32，被動齒輪齒數Z2=75，模數m=12，壓力角a=22.5°，靜傳遞誤差的常數項、諧波項分別為e0=0、er=0.108 mm。輪軌黏著特性曲線中，選取um=0.25，sm=0.02，ku=-0.25。

基于勢能原理[13-15]，綜合考慮輪齒彎曲變形、剪切變形、軸向壓縮變形、赫茲接觸變形、以及輪體變形對應的嚙合線上的等效剛度。進而獲得齒輪綜合時變嚙合剛度，并將其展開為傅里葉級數形式，結果如圖3所示。其中幅值kj、相位角φj(j=0～4)的值如表2所示。

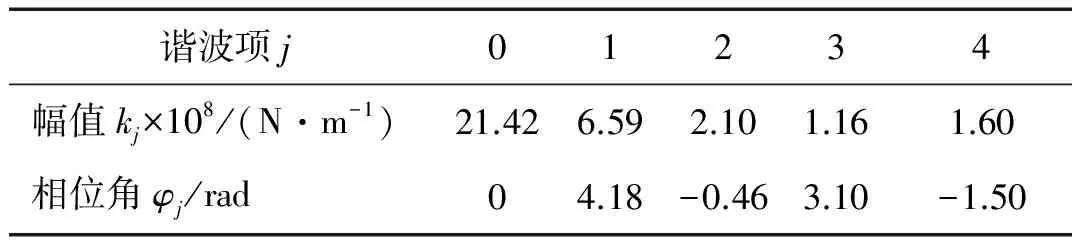
表2 嚙合剛度各階諧波幅值與相位角Tab.2 Harmonic amplitude and phase angle of mesh stiffness

當φ1-φ=π時，忽略θ的微小變化，仿真得到不同f2、f3、f4、ke1、μ下，系統主共振的頻率響應曲線如圖4-圖8所示。

由圖4～圖8可知，隨著無量綱參數f2的增大，頻響曲線呈現向右平移的趨勢，且幅值有所變化。由此可見，輪軌黏著力的動態變化值影響著系統的主共振發生的頻率和振幅。同時，系統的非線性特性使得主共振的頻響曲線產生多值情況，且無量綱參數f3、f4、ke1的減小或μ的增大有利于減小多值區域的產生。此外，f3、f4、ke1的減小對振幅有一定的抑制作用。所以，誤差速度項激勵的系數F3、誤差諧波項的幅值er、一次諧波剛度的比值ke1的減小不僅有利于減小多值區域的產生，也對振幅有一定的抑制作用。阻尼的增大也有利于減小系統多值區域的產生。

圖4 不同f2時的頻響曲線Fig.4 Frequency response curve with different f2

圖5 不同f3時的頻響曲線Fig.5 Frequency response curve with different f3

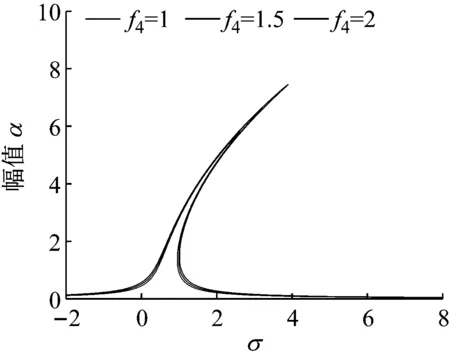
圖6 不同f4時的頻響曲線Fig.6 Frequency response curve with different f4

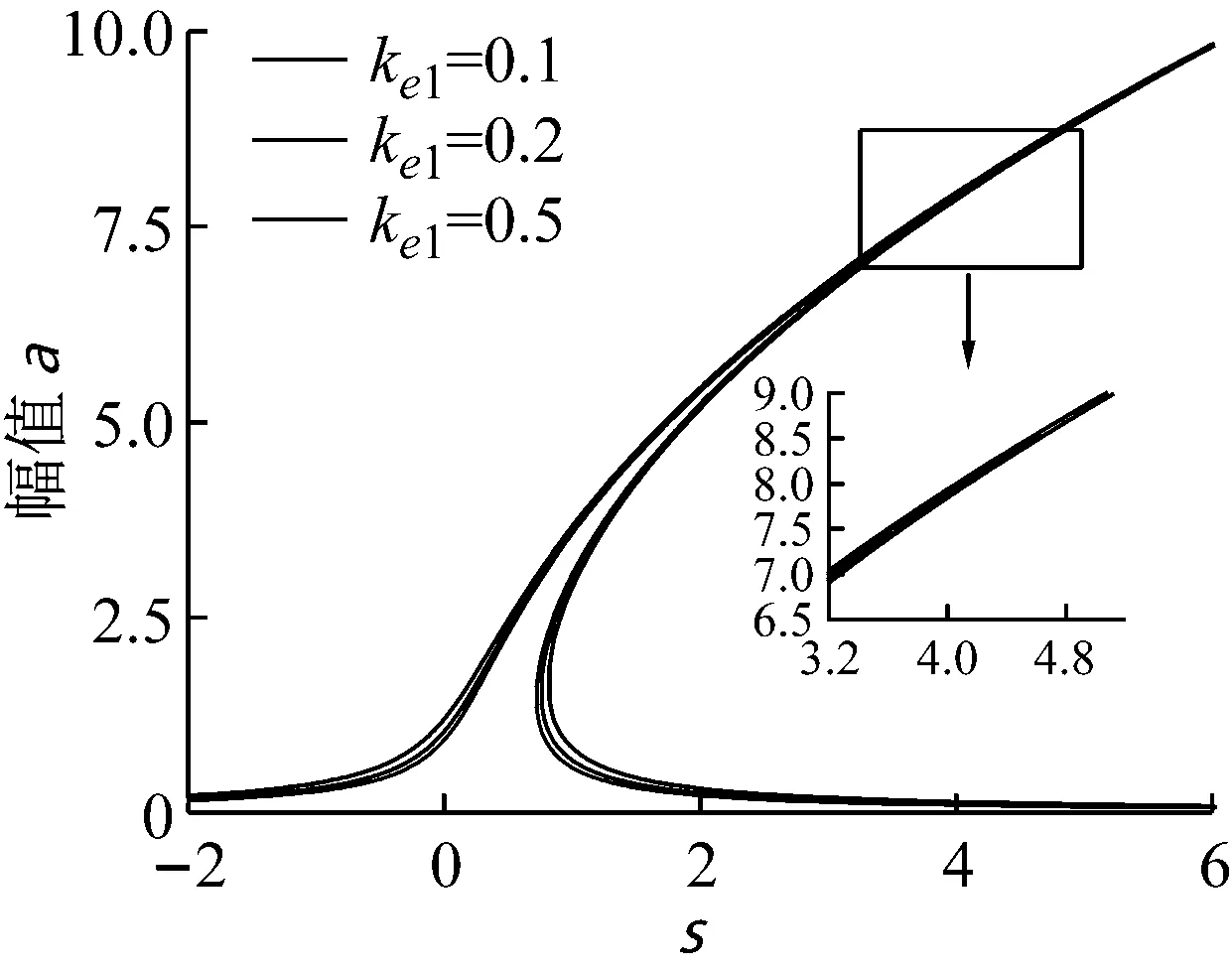
圖7 不同ke1時的頻響曲線Fig.7 Frequency response curve with different ke1

圖8 不同μ時的頻響曲線Fig.8 Frequency response curve with different μ

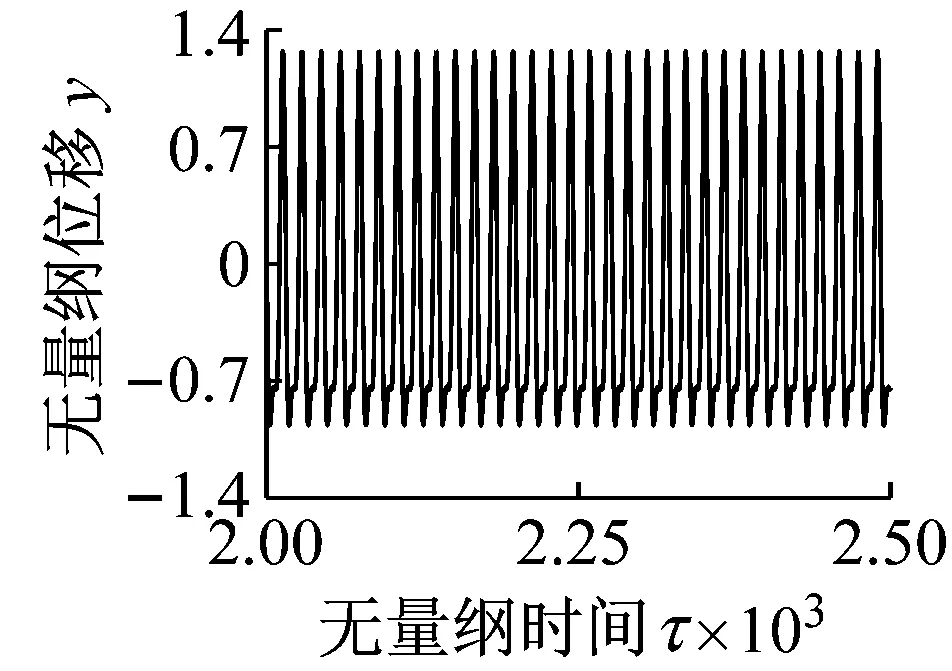
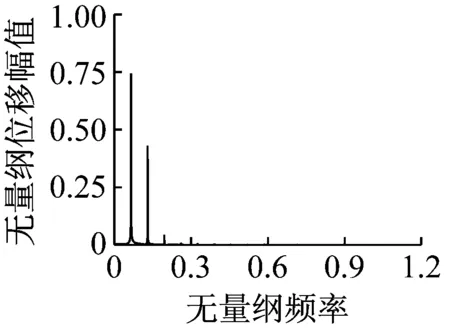
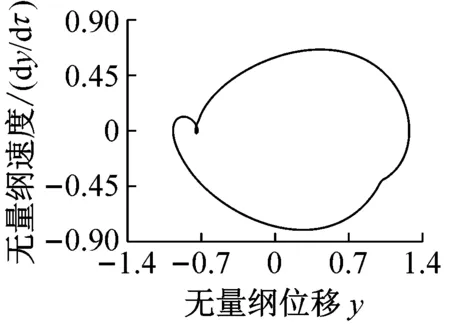
設系統的初始條件為：y(0)=dy(0)/dτ=0。當?=w1，不計齒輪嚙合阻尼cm，靜平衡位置處的蠕滑率s0分別為0.012、0.035，得到考慮輪軌黏著力的動態變化時機車驅動系統主共振時的時域響應、頻譜圖、相平面圖和輪軌黏著系數的變化曲線分別如圖9、圖11所示。當靜平衡位置處的蠕滑率s0分別為0.012、0.035，輪軌黏著力為恒值時，得到機車驅動系統主共振的時域響應、頻譜圖和相平面圖分別如圖10、圖12所示。

(9a)

(9b)

(9c)

(9d)圖9 s0=0.012，輪軌黏著力變化時Fig.9 The results when s0=0.012 considerating the change of wheel-rail adhesion force

對比圖9和圖10可知，當s0=0.012時，靜平衡位置處的黏著系數處于黏著段。在無量綱時間[2 000～2 500]范圍內,考慮輪軌黏著力的動態變化時主共振位移的最大值較輪軌黏著力為恒值時減小了約35.35%。且考慮輪軌黏著力的動態變化與否對系統振動的頻譜圖和相軌跡具有巨大影響。

對比圖11和圖12可知，當s0=0.035時，靜平衡位置處的黏著系數處于滑動段。在無量綱時間[2 000～2 500]范圍內,考慮輪軌黏著力的動態變化時主共振位移的最大值較輪軌黏著力為恒值時增大了約115.55%。且考慮輪軌黏著力的動態變化與否時，兩者的頻譜圖和相軌跡存在較大差異。

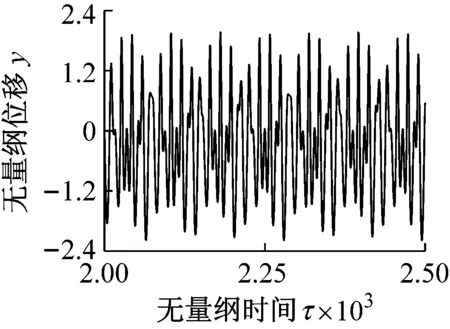
(10a)

(10b)

(10c)圖10 s0=0.012，輪軌黏著力為恒值Fig.10 The results when s0=0.012 and wheel-rail adhesion force is a constant

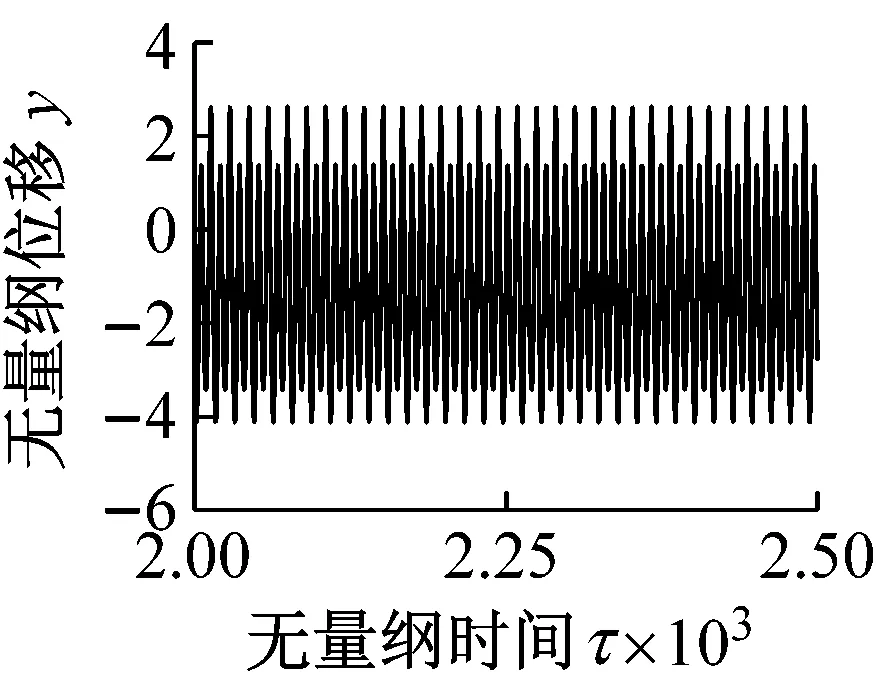
(11a)

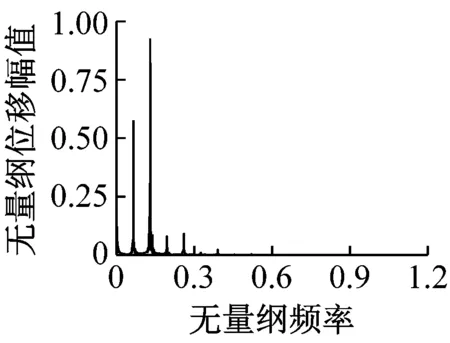
(11b)

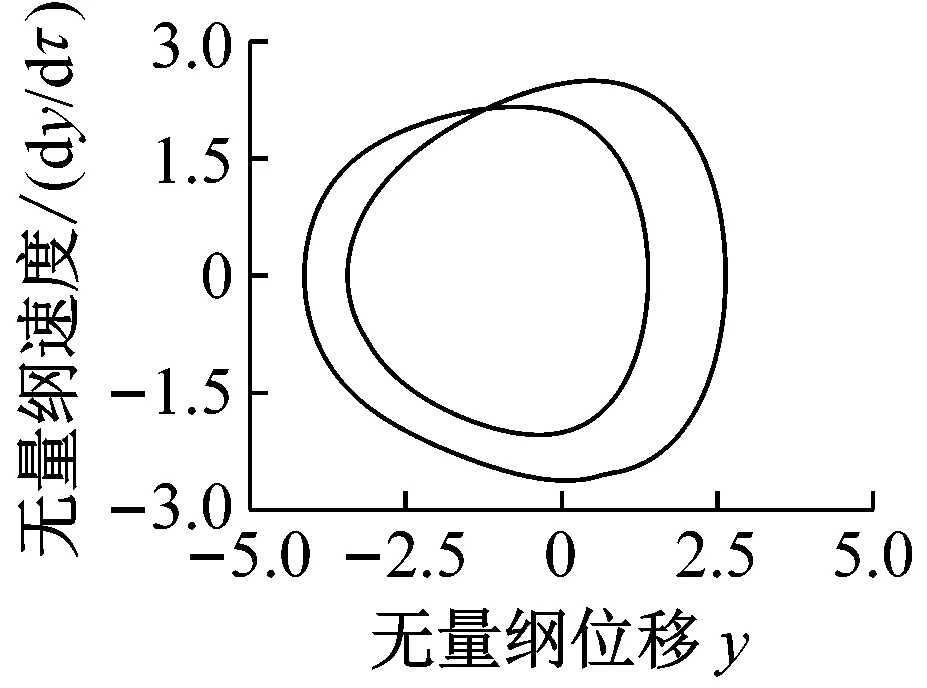
(11c)

(11d)圖11 s0=0.035，輪軌黏著力變化時Fig.11 The results when s0=0.035 considerating the change of wheel-rail adhesion force

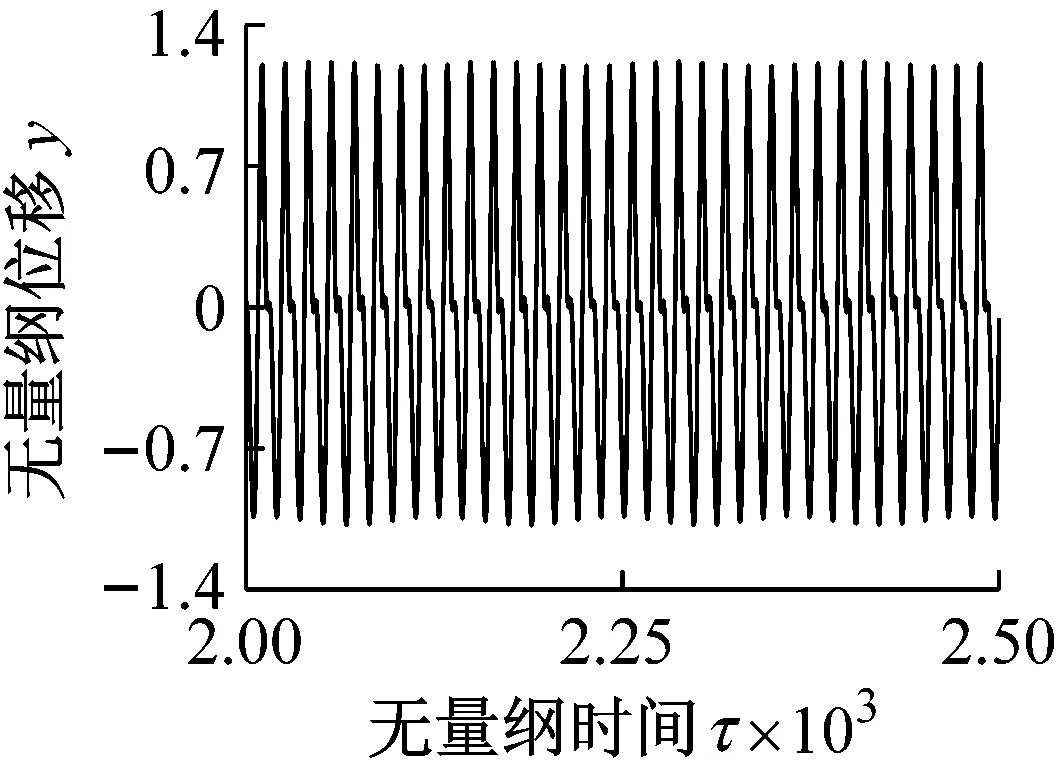
(12a)

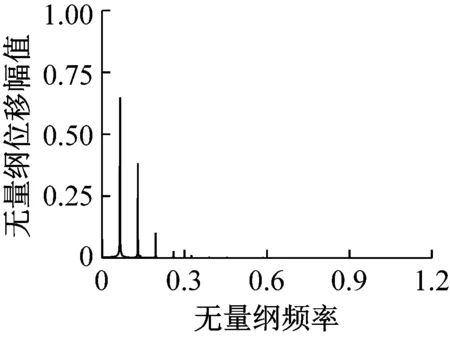
(12b)

(12c)圖12 s0=0.035，輪軌黏著力為恒值Fig.12 The results when s0=0.035 and wheel-rail adhesion force is a constant

5 結 論

本文考慮了機車驅動系統內部齒輪嚙合的靜傳遞誤差、時變嚙合剛度和齒側間隙，建立了內部齒輪嚙合動態激勵和外部輪軌黏著力激勵共同作用下系統的動力學模型及方程，采用解析法和數值仿真相結合的方法，研究了機車驅動系統主共振時的振動特性，通過分析得出以下結論：

(1) 采用解析法—多尺度法進行求解，獲得了輪軌黏著下計及齒輪嚙合特性的機車驅動系統主共振時的頻率響應方程，可為系統主共振的頻響特性提供理論依據。

(2) 通過數值仿真系統參數變化對系統主共振頻響曲線的影響得知：輪軌黏著力的動態變化值會影響系統主共振產生的頻率和幅值；系統的非線性特性使得主共振的頻響曲線產生多值情況，且誤差速度項激勵的系數F3、誤差諧波項的幅值er、一次諧波剛度的比值ke1的減小或阻尼的增大有利于減小多值區域的產生，同時，F3、er、ke1的減小對振幅有一定的抑制作用。

(3) 通過數值仿真不同黏著系數s0下系統主共振的振動響應(不計齒輪嚙合阻尼時)得知：在無量綱時間[2 000～2 500]范圍內，當s0=0.012，考慮輪軌黏著力的動態變化時位移的最大值較輪軌黏著力為恒值時減小了約35.35%；當s0=0.035，考慮輪軌黏著力的動態變化時位移的最大值較輪軌黏著力為恒值時增大了約115.55%；且兩種情況下，考慮輪軌黏著力的動態變化與否對系統振動的頻譜圖和相軌跡具有較大影響。

參 考 文 獻

[1] AL-SHYYAB A, KAHRAMAN A.Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: sub-harmonic motions[J].Journal of Sound and Vibration,2005, 279(1):417-451.

[2] SHEN Yongjun,YANG Shaopu,LIU Xiandong.Nonlinear dynamics of a spur gear pair with time-varying stiffness and backlash based on incremental harmonic balance method[J]. International Journal of Mechanical Sciences,2006,48(11): 1256-1263.

[3] 魏靜,孫偉,褚衍順,等.斜齒輪系統分岔與混沌特性及其參數影響研究[J].哈爾濱工程大學學報,2013,34(10):1301-1309.

WEI Jing,SUN Wei,CHU Yanshun,et al.Bifurcation and chaotic characteristics of helical gear system and parameter influences[J]. Journal of Harbin Engineering University,2013,34(10):1301-1309.

[4] 李應剛,陳天寧,王小鵬,等.外部動態激勵作用下齒輪系統非線性動力學特性[J].西安交通大學學報,2014,48(1):101-105.

LI Yinggang,CHEN Tianning,WANG Xiaopeng,et al.Non-linear dynamics of spur gear pair under external periodic excitation[J]. Journal of Xi’an Jiaotong University,2014,48(1):101-105.

[5] FARSHIDIANFAR A,SAGHAFI A.Global bifurcation and chaos analysis in nonlinear vibration of spur gear systems[J]. Nonlinear Dynamics,2014,75(4):783-806.

[6] GOU Xiangfeng,ZHU Lingyun,CHEN Dailin.Bifurcation and chaos analysis of spur gear pair in two-parameter plane[J]. Nonlinear Dynamics,2015,79(3):2225-2235.

[7] 黃冠華,張衛華,宋紓崎,等.高速列車齒輪傳動系統諧振分析[J].交通運輸工程學報,2014,14(6):51-58.

HUANG Guanhua,ZHANG Weihua,SONG Shuqi,et al. Harmonic resonance analysis of gear transmission system for high speed train[J].Journal of Traffic and Transportation Engineering, 2014, 14(6): 51-58.

[8] 王曉筍,巫世晶,周旭輝,等.含側隙非線性齒輪傳動系統的分岔與混沌分析[J].振動與沖擊,2008,27(1):53-56.

WANG Xiaosun,WU Shijing,ZHOU Xuhui,et al.Bifurcation and chaos in a nonlinear dynamic model of spur gear with backlash[J]. Journal of Vibration and Shock,2008,27(1):53-56.

[9] YAO Yuan,ZHANG Hongjun,LI Yeming,et al.The dynamic study of locomotives under saturated adhesion[J]. Vehicle System Dynamics,2011,49(8):1321-1338.

[10] 姚遠,張紅軍,羅赟,等.機車傳動系統扭轉與輪對縱向耦合振動穩定性[J].交通運輸工程學報,2009,9(1):17-20.

YAO Yuan,ZHANG Hongjun,LUO Yun,et al.Torsional-longitudinal coupling vibration stability of drive system for locomotive[J]. Journal of Traffic and Transportation Engineering, 2009,9(1):17-20.

[11] 張晨旭,楊曉東,張偉.含間隙齒輪傳動系統的非線性動力學特性的研究[J].動力學與控制學報,2016,14(2):115-121.

ZHANH Chenxu,YANG Xiaodong,ZHANG Wei.Study on non-linear dynamics of gear transmission system with clearance[J]. Journal of Dynamics and Control,2016,14(2):115-121.

[12] THEODOSSIADES S,NATSIAVAS S.Non-linear dynamics of gear-pair systems with periodic stiffness and backlash[J].Journal of Sound and Vibration,2000,229(2):287-310.

[13] CHEN Zaigang,SHAO Yimin.Dynamic features of a planetary gear system with tooth crack under different sizes and inclination angles[J].Journal of Vibration and Acoustics,2013, 135(3):031004.

[14] LIANG X H, ZUO M J, PANDEY M.Analytically evaluating the influence of crack on the mesh stiffness of a planetary gear set[J].Mechanism and Machine Theory,2014,76:20-38.

[15] WAN Zhiguo,CAO Hongrui, ZI Yanyang,et al.An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack[J].Engineering Failure Analysis,2014,42:157-177.