含進化的適應性測度的做市商庫存動態模型研究

楊 志，王 婧

(伊犁師范學院數學與統計學院，新疆伊寧 835000)

1 研究背景

近些年，在金融市場中關于異質代理商模型的研究受到越來越多的學者的關注，尤其是在Brock and Hommes[1]的引導下，得到了進一步的研究，大多數學者考慮市場中有兩類投資者：基本面分析者和技術分析者，投資于一支無風險資產和一支風險資產，由于投資者對未來價格變化的不確定性，進而產生不同的信念，采用不同的交易策略，進而產生不同的期望價格，通過均值-方差最大化來決定投資數量，投資者之間相互博弈，在市場中進行交易，再利用做市商來出清市場價格.

由于做市商的不同角色，產生了不同模式的出清市場價格，如Carl[2]利用市場供給來出清市場價格，Carl[3]又提出做市商利用庫存來出清市場價格，做市商扮演了不同的角色：投資者和供應商.Mei Zhu[4]也考慮了在做市商扮演兩種角色下的金融市場模型，做市商對于市場穩定性所起的不同作用.

波動聚集性作為金融市場數據的典型特征之一，很多學者通過建立不同的模型來模擬市場數據特征，如Brock and Hommes[1]提出度量交易策略的適應性測度，但其沒有考慮風險因素，Gaunersdorfer[5]考慮將風險加入，即風險調整后的適應性測度；Roberto Dieci and Xue-Zhong He[6]通過改變市場分數的不同組合方式，對模型作進一步的修改，以此希望更好地模擬真實市場.

本文建立做市商庫存動態模型，該模型含有兩類投資者：基本面分析者和技術分析者，做市商利用庫存出清市場價格，同時做市商扮演供應商和投資者的角色，考慮動態的市場分數，同時采用經風險調整后的適應性測度，以此來決定投資者在市場中所占的比例；利用差分系統理論與分支理論，考慮系統的穩定性區域，以及分析主要參數α,β,γ對系統穩定性的影響，進而說明相應參數在真實系統的作用，更好地解釋真實市場的數據特征.

2 建立模型

參考Carl[7]建立的隨機模型：

(1)

這里考慮市場中有三類投資者：基本面分析者、圖表分析者、做市商.

2.1 基本面分析者，技術分析者

考慮其對未來價格條件期望與Carl[7]建立的模型一致.

2.2 做市商

作為市場投資者，為了得到自己的既得利益，設置投資組合最優化，達到目標庫存：

(2)

其中，α表示做市商調整庫存的速度.作為供應商，做市商有義務保證市場的流動性，維護市場的穩定.

2.3 市場分數

考慮基本面分析者和圖表分析者所占的市場分數分別為q1，t和q2，t，并且分為固定部分與時變部分，即不改變投資策略和投資策略隨時間改變而改變[4]，其中n1和n2分別為投資策略不改變者所占的比例，n1，t和n2，t分別為投資策略改變者所占的比例，并且n1+n2=1，n1，t+n2,t=1，設γ為不改變投資策略所占的比例，則1-γ為改變投資策略所占的比例；記n0=n1-n2，mt=n1,t-n2,t，則有：

(3)

假設nh,t由離散選擇概率來確定：

(4)

其中，β表示選擇強度，用以衡量不同投資者對于不同投資策略的傾向程度；Ch表示h類投資者為其策略選擇所產生的固定費用；Uh,t為t時第h類投資者獲得的利潤，用來衡量該交易策略的性能，稱作適應性測度.采用發展的適應性測度[8]，即經過風險調整后的適應測度.

(5)

其中，η為適應測度的記憶強度，則：

(6)

2.4 市場出清

假設做市商通過調整庫存出清市場價格：

(7)

其中，zt=q1,tz1,t+q2,tz2,t.

綜上得到隨機離散動力系統模型為：

(8)

3 確定性動力系統的討論

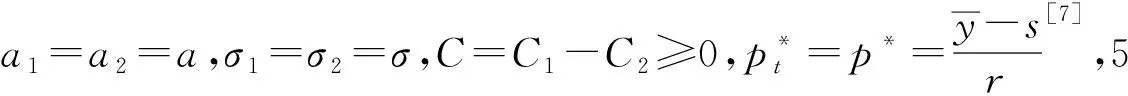
(9)

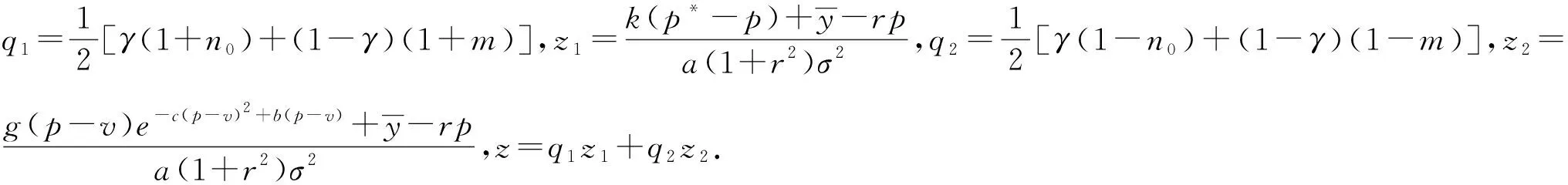
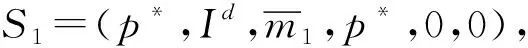
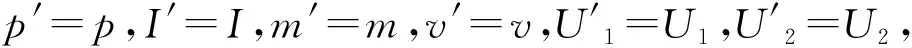
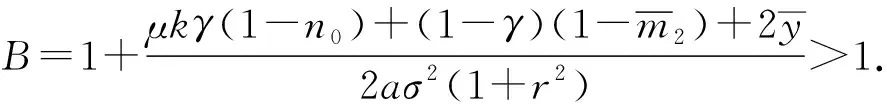
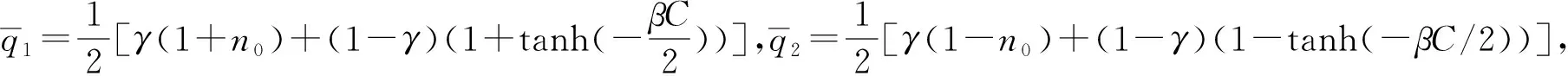
由于做市商在市場的不同角色，分兩種情況分別來進行討論：

(i)當α=1，做市商迅速將下一時期庫存調整為目標庫存水平.

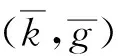
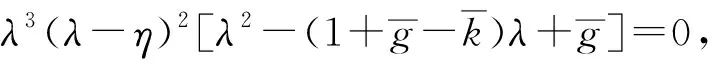
(10)

即S1局部漸近穩定的條件.

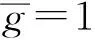
推論1 基本均衡點S1在(β,γ)的局部漸近穩定區域為：

(ii)當0<α<1的一般情形.

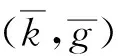
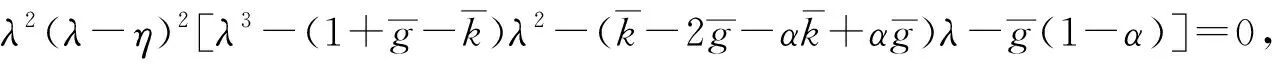
引理1 已知特征方程為λ3+c1λ2+c2λ+c3=0，則相應的系統在不動點處漸近穩定為：

由此，可得到該系統模型在不動點S1處的漸近穩定區域為：

推論2 基本均衡點S1在(β,α)局部漸近穩定區域如下：

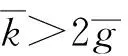
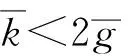
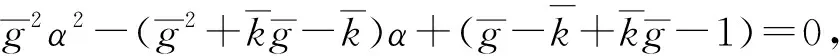
4 結論

本文建立了做市商庫存動態模型，利用差分系統理論，考慮系統的穩定性區域，分析了主要參數α,β,γ對系統穩定性的影響，得到如下結論：

當α=1時，做市商快速將下一期庫存調整為目標庫存，則基本均衡點穩定區域主要依賴于基本面分析者和技術分析者；當0<α<1且α取不同值時，得到相近的穩定區域，說明做市商對于市場的穩定性作用有限，主要依賴于基本面分析者和技術分析者.

當γ取不同值，其取值為0.5左右，堅持投資策略改變者與堅持投資策略不改變者的比例相差不大時，產生的穩定區域為兩部分；當γ較大或者較小，一方作用比另一方作用較強時，穩定區域為一部分，且分支邊界關于做市商的作用強度對稱.

[參考文獻]

[1]Brock W,Hommes C.Heterogeneous beliefs and routs to chaos in a simple asset pricing model[J].Journal of Economic Dynamic & Control,1998(22):1235-1274.

[2]Chiarella C,He X-Z.Heterogeneous beliefs,risk and learning in a simple asset pricing model[J].Computational Economics 2002(19):95-132.

[3]Chiarella C,He X-Z.Heterogenous beliefs,risk and learning in a simple asset pricing model with a market maker[J].Macroeconomic Dynamics,2003(7):503-536.

[4]Zhu M,Chiarella C,He X Z,et al.Does the market maker stabilize the market?[J].Physica A:Statistical Mechanics and its Applications,2009(15):3164-3180.

[5]Gaunersdorfer A,Hommes C.A nonlinear structural model for volatility clustering[J].Cendef Working Papers, 2000(00-01):265-288.

[6]Dieci R,Foroni I,Gardini L,et al.Market mood,adaptive beliefs and asset price dynamics[J].Chaos,Solitons and Fractals,2006(29):520-534.

[7]Chiarella C,He X,Wang D.Stock price and market maker inventory dynamics with heterogeneous beliefs[C].Working Paper,School of Finance and Economics,University of Technology,Syde-Ney,2011.

[8]Gaunersdorfer A,Hommes C H,Wagener F O O.Bifurcation routes to volatility clustering under evolutionary learning[J].Journal of Economic Behavior & Organization,2001(1):27-47.

[9]Sonis M.Critical bifurcation surfaces of 3D discrete dynamics[J].Discrete Dynamics in Nature & Society,1999(4):333-343.

[10]王聯,王慕秋.常差分方程[M].烏魯木齊:新疆大學出版社,1991:202-204.