直接radau配置的多階非線性模型預測聚合反應控制

孫京誥 ，占子赫

1.華東理工大學 信息科學與工程學院，上海 200237

2.華東理工大學 化工過程先進控制和優化技術教育部重點實驗室，上海 200237

1 引言

半間歇聚合反應的溫度控制一直是過程控制研究的熱點問題[1-2]。非線性模型預測控制（Nonlinear Model Predictive Control，NMPC）具有顯示處理系統約束和在不確定環境下優化控制的共性機理，使其成為繼PID控制之后在控制工程中被廣泛應用和研究的先進控制技術之一[3]。NMPC運用更加合理的目標函數，比如最小化批次時間，使得反應過程更加注重經濟效益而不是過度地追求與目標溫度的溫差最小化[4]。然而在實際的化工過程中，往往存在實際參數與模型不匹配的情況，這使得NMPC的性能極大地下降。一類基于不確定預測模型魯棒模型預測控制旨在彌補傳統NMPC的不足，近年被眾多學者廣泛研究。最早有學者采用開環的min-max策略，即在通過最小化最差情況下的目標函數得到控制輸入[5]。這種方法被證實不僅具有一定程度的保守性，而且由于基于開環控制的假設與真實的閉環系統不匹配，導致其并不具備魯棒性。為了攻克這個問題，有學者提出了閉環min-max策略[6]，但是由于內在的計算復雜度，該算法在實際應用中的成功率有限。Tube-based mpc運用副控制器保證在不確定因素存在的情況下滿足限制條件并保證控制的穩定性，但是該方法不能保證是最優控制[7]。近年來，多階非線性模型預測控制（Multi-stage Nonlinear Model Predict Control，Multistage NMPC）在基于閉環魯棒MPC和運用場景樹對不確定量的建模的思想上產生[8-9]。在這個策略中，不確定量表示成場景樹的形式，未來的控制變量作為輔助變量來優化，以此來降低該策略的保守性，Multi-stage NMPC已經被證實具備很好的解決傳統NMPC面臨的模型參數常量與實際不匹配問題的能力。

NMPC是一類基于在線優化的控制算法，其在線優化計算速度直接關系到能否成功應用。相比于線性模型預測控制，NMPC計算的最大困難在于要在有限的采樣時間內計算一個非凸的非線性規劃問題（Nonlinear Programming，NLP）[3]。求解該問題的計算量隨決策變量的維數呈指數增長。故對于規模更大的Multi-stage NMPC，快速高效的求解方法是其能否成功應用的關鍵。現有的NMPC數值算法大致分為序貫法和聯立法兩種[10]，聯立法也稱為直接轉化法，它通過同時離散狀態變量和控制變量將問題轉化為NLP。這樣將DAE或ODE系統的求解和優化問題結合在一起，避免了中間解的尋找，并且具有更靈活的處理路徑不等式的能力和處理不穩定和病態條件問題的能力[11]。有限元正交配置（Orthogonal Collocation on Finite Element，OCFE）是聯立法常用的局部離散方法，具有精度高，計算量小的特點，在動態優化問題中有廣泛的應用。此外，配置點的選擇合理與否，不僅關系著解的精確性，也關系著運算的復雜度，正交配置中常用的配置點有radau點、legendre點和lobatto點[12]。

本文提出了多階非線性模型預測半間歇聚合反應控制器設計方法，將NMPC滾動優化問題描述成最優控制問題，其目標函數綜合考慮了溫度偏移和批次反應時間。為了提高動態優化問題求解效率，采用基于有限元正交配置的聯立法求解，通過實驗選取合適的radau配置點，將狀態變量和控制變量同時離散化，推導出基于multi-stage NMPC的可求解 NLP問題，然后借助IPOPT工具箱調用內點法求解[13]。

2 Multi-stage NMPC

Multi-stage NMPC最重要的理論基礎是不確定量可以使用離散場景樹的形式表示出來，如圖1所示，在每一個節點的每一個分支都代表了一種未知的不確定因素和選擇的控制變量對系統的影響，這些不確定因素可能是參數誤差或者外部擾動。通過這個方程，在未來采樣時刻將得到新的信息，因此最優化的控制變量可以當作抵消各種不確定參數的輔助變量，這種方法降低該策略的保守性。盡管在每個階段場景樹都有不同分支，但是這不表示在每個采樣點不確定量是變化的。這只是表示如果不確定量如果在第K階段是未知的，那么在第K+1階段也是未知的。因此在下一個采樣點，新的場景樹將被生成以求出下一個時刻的控制量。

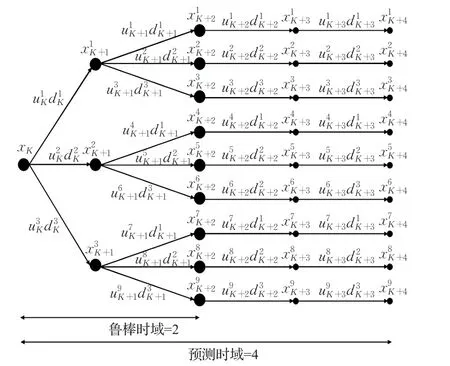
圖1 Multi-stage NMPC的場景樹示意圖

由于場景樹的離散設定，在場景樹的設定下一個帶有不確定參數的不確定非線性系統表述如式（1）：

上式表明k時刻的狀態取決于前一個狀態，相應的控制輸入以及不確定參數簡潔起見，所有的不確定參數和場景樹都設置為統一的形式，在所有的節點上都有相同數目的分支。本文約定在一個節點處，一個不確定量用三個分支來表示，假設有m個不確定量，易知在每個節點需要有3m個分支，這樣隨著預測時域的增大，優化問題的規模也級數倍增長。為了避免場景樹的規模過大而帶來不必要的運算，設置魯棒時域NR，在魯棒時域后場景樹將不再分支，如圖1中，魯棒時域設置為2。場景樹中出現的(j,k)統一用符號S表示。每條從節點xk到葉子節點的路徑稱為一個場景。

在上述符號表述的基礎上，基于場景樹的最優化問題可如式（2）描述：

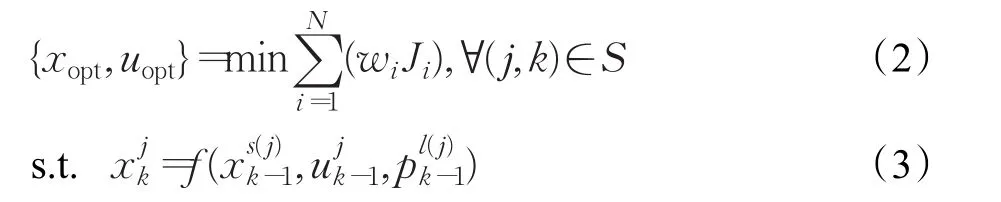
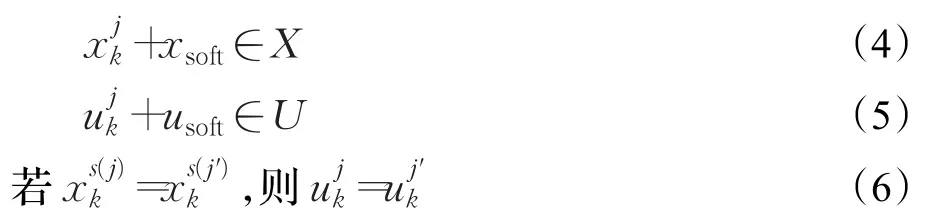
公式中，N表示場景的數目，Ji和wi分別表示每個場景Si的目標方程和其相應權重。X、U分別表示狀態變量和控制變量的取值范圍，xsoft和usoft分別表示對狀態變量和控制變量的軟化約束（Soft constraints）。式（6）稱為非預期約束條件，表示在相同的分支處，設定控制量相同。對于一般的間歇反應模型，單個場景的目標方程有如下形式：

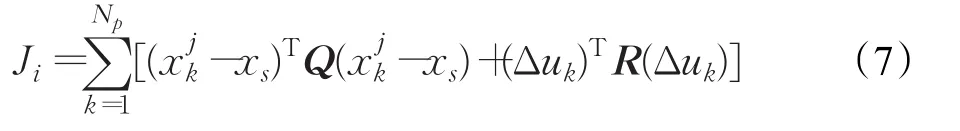
其中NP表示預測時域，Q和R為對角加權矩陣，目標方程的第一項表示狀態變量跟蹤設定值的懲罰項。第二項表示對控制變量變化量懲罰項，旨在防止控制變量劇烈變化。此外，限制條件包括對狀態變量和控制變量取值范圍的限制，同時，動態模型也作為最優化問題的約束條件。

3 將動態優化問題轉化成NLP問題

使用聯立法求解動態優化問題需要精確的離散方法以保證對連續的軌跡的逼近精度。為了使得到的NLP問題規模不至于過大而增加求解難度，一般情況下不采用全局的離散化方法。OCFE是一種局部的離散化方法，屬于隱式Runge-Kutta法，可以提供高階的精度和良好的穩定性。在一段采樣區間內，定義有限元個數為nκ，有限元長度hκ。在每個有限元上通過Lagrange插值對狀態變量，控制變量進行逼近：

其中(t)表示在場景樹的(j,k)位置上，處于第κ個有限元區間內的狀態變量值，(t)亦然。 τ∈[0,1]表示配置點。設nθ為插值的階次，則一個有限元內的配置點 用 τ0,…,τnθ表示，本文選用Radau配置點，具體配置點信息將在第 5章給出。 lθ(τ)和 lˉθ(τ)分別表示狀態變量和控制變量的Lagrange插值多項式，可用如下形式表示：

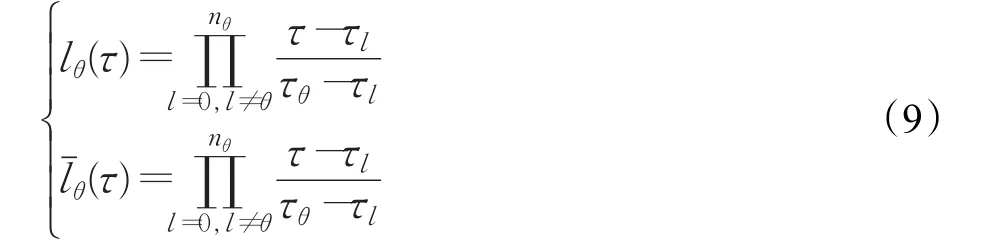
Lagrange多項式插值具有如下性質：

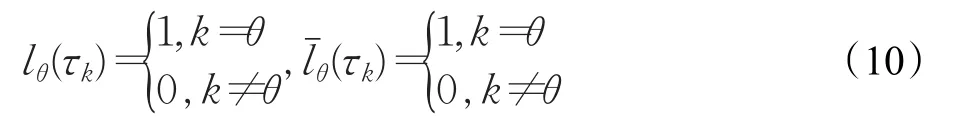
定義tk,κ,θ為第k階段第κ個有限元第θ個插值點的時間，為第k階段第κ個有限元的終端時間，該時間僅僅和有限元的個數nκ和插值階次nθ相關。于是，在場景樹中每個正交配置點上，滿足

于是可以得到離散化后的NLP問題：

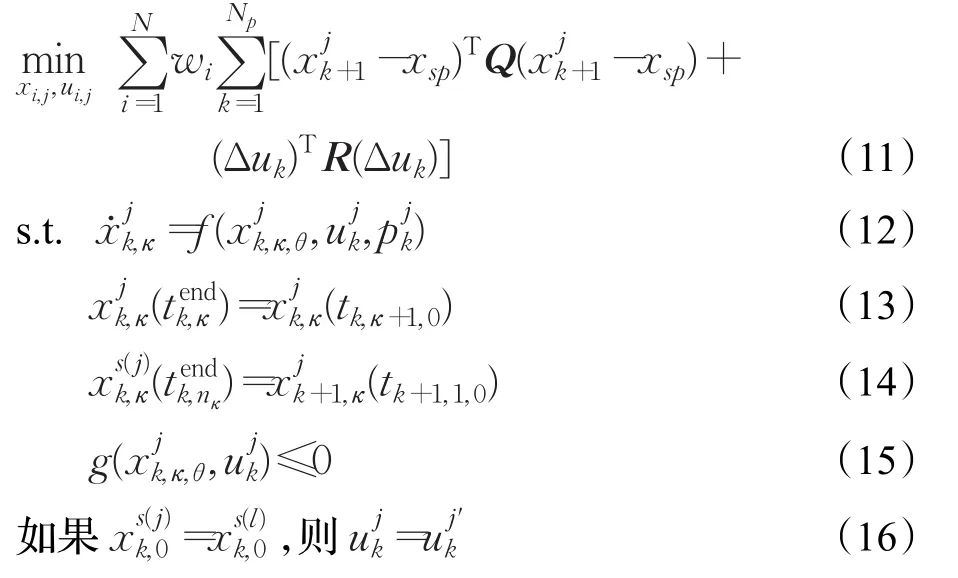
其中，式（12）通過將每個有限元微分得到，其中微分變量需要保持狀態的連續性，式（13）保證了每個相鄰有限元之間的連續性，式（14）保證了相鄰控制時域內的連續性。狀態變量約束和控制變量約束條件由式（15）給出。

4 半間歇聚合反應模型

為了驗證提出的算法的可行性，本文對一種間歇性化工聚合反應進行研究，該模型來自于一個實際的化工間歇聚合反應模型，它的機理模型由BASF SE公司提供。

4.1 機理模型

該系統主要由一個反應釜，夾套以及一個外部熱轉換器（External Heat Exchanger，EHE）組成，夾套和EHE可以用來控制反應釜內的溫度。其工藝圖如圖2。在一個批次的反應中，開始階段將反應所需的引發劑，水等反應所需物質加入反應釜內，將釜溫加熱到設定溫度后進入進料階段，即開始持續向釜內加入單體，當加入的單體達到一定質量時停止進料，進入保持階段，直到產生到規定質量的聚合物后反應停止。

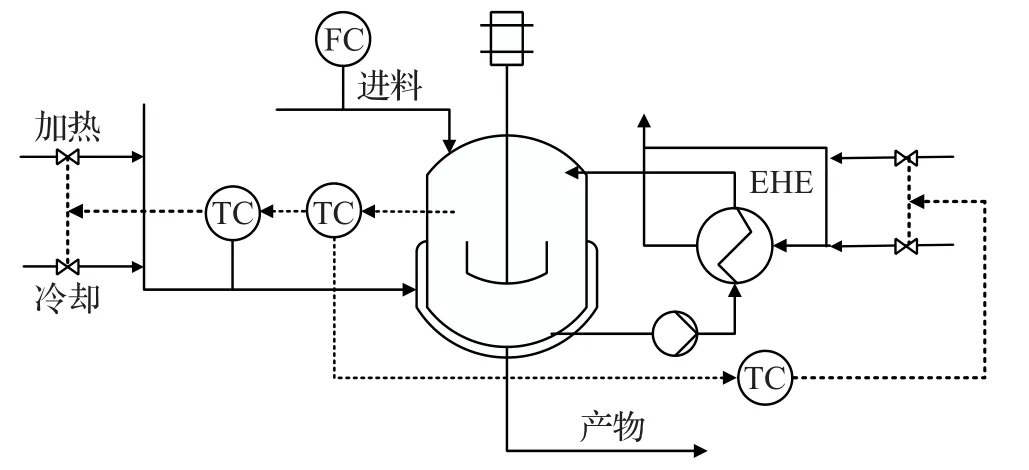
圖2 半間歇式聚合反應工藝圖

根據物料守恒和能量守恒，其機理模型由主要由8個常微分方程構成，如式（17）～（24）所示：

該機理模型包括水mW，單體mA和聚合產物mP的物料守恒方程以及反應釜內溫TR，管道溫度TS，夾套溫度TM，外部熱轉換器溫度TEK和冷卻劑在熱轉換器的出口溫度TAWT的能量守恒方程。反應過程中有三個控制變量，分別是進料速率mF，外部熱交換器入口溫度夾套入口冷卻劑溫度TINM。

U表示反應釜內聚合物與單體的比例：

mges表示釜內物質的總質量：

kR1、kR2分別表示表示釜內的反應速率和外部熱轉換器的反應速率，如式（27）、（28）所示：

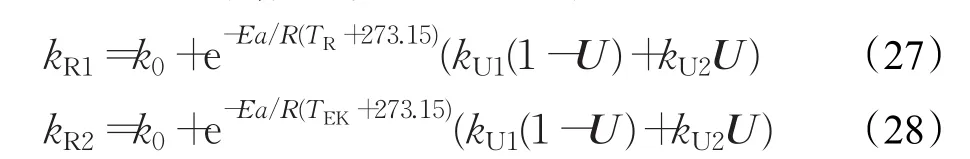
kK表示反應釜內的混合物總傳熱系數，由式（29）給出：

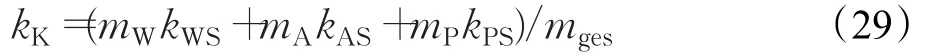
mA,R表示釜內的單體質量，由式（30）得出：

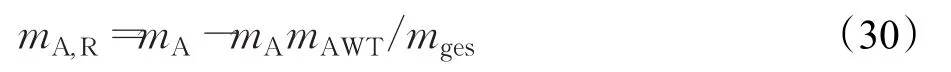
4.2 控制目標

在一個批次反應過程中，在滿足安全條件限制和產物質量的前提下，要在盡可能短的時間內通過調整mF、TINAWT、TINM使反應安全穩定迅速地進行。溫度的控制在聚合反應中占據了很重要的位置，它和聚合產物的質量息息相關。在本問題中，反應釜的溫度應該被控制在設定溫度Tset=(363.15±2.0)K范圍內。在真實的反應過程中，出于對安全性和反應器材耐受能力的考慮，反應過程溫度還需要滿足安全限制。在本模型中，為了避免冷卻失敗的情況，反應釜最高溫度被限制在382.15 K。在任意時刻反應釜的安全溫度由式（31）給出：

此外，加入反應釜的單體的最大質量為30 000 kg。進料階段投入單體，當添加完所需的所有的單體，反應進入保持階段，如果聚合物的質量達到20 680 kg，則反應停止。若在給定的單體范圍內沒有生產出規定質量的聚合物則反應失敗。在真實的系統中，通常模型的參數不能被準確地測量。在本模型中，有兩個關鍵的參數：反應熱焓ΔHR和反應速率k0，這兩個參數通常會在其給定值的±30%內變化，且在一個批次的反應過程中值不變。模型的狀態變量的初始值與取值范圍和控制變量的取值范圍分別如表1，表2所示。

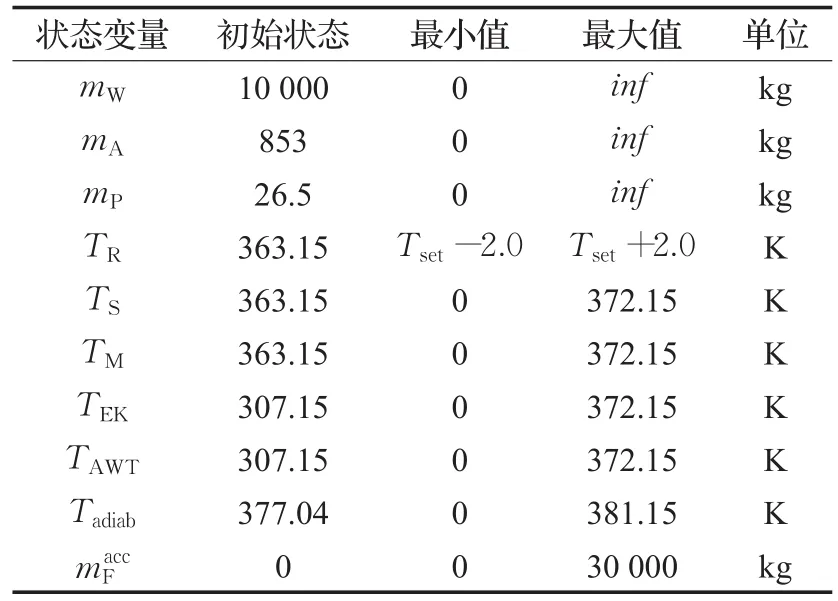
表1 狀態變量初始值和取值范圍

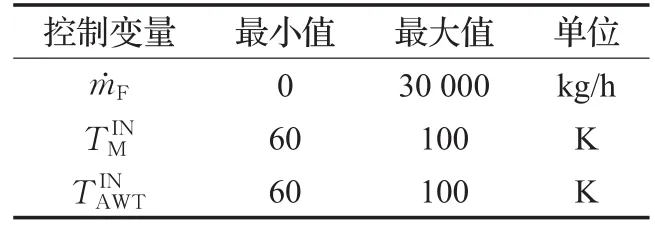
表2 控制變量取值范圍

5 仿真分析

所有的計算都運行在Windows環境臺式電腦（Inter Core i7-6700K@4.00 GHz 16 GB DDR4 2 801 MHz）。Multi-stage NMPC所產生的NLP問題都采用最優化工具包IPOPT來求解，IPOPT工具包內部使用內點法對最優化問題進行求解。設定Multi-stage NMPC和NMPC的采樣時間tstep=50 s，預測時域Np=10，設定Multi-stage NMPC的魯棒時域NR=1。反應模型中兩個不確定反應熱焓ΔHR和反應速率k0在其給定值的±30%內變化，其真實值分表由，表示。由于有兩個不確定量，在魯棒時域內，場景樹的每個節點都有9個分支，分支的不確定參數以最壞情況和標準情況的組合，即=(0.7,1.0,1.3)×ΔHR分別與=(0.7,1.0,1.3)×k0組合得到的9種可能。優化問題目標方程綜合考慮了溫度跟蹤和反應的速率，設定式（6）中-1,100,0,0,0,0,0,0],R=diag[0.2,0.03,0.02]。此外，仿真過程中假定所需要的變量都可以被準確地測量。

5.1 正交配置點的選取

配置點τ的選擇對求解的精度，速度以及解的存在與否都有很大的影響[15]。若采用等間隔方式選取配置點，當點過于密集時可能產生龍格（Runge）現象[14]。本文選擇radau點作為配置點，使用radau配點的OCFE可以有效避免龍格現象，并獲得平滑的逼近軌跡，且相比于legendre點，radau點可以提供更佳的穩定性。radau配置點取值如表3。

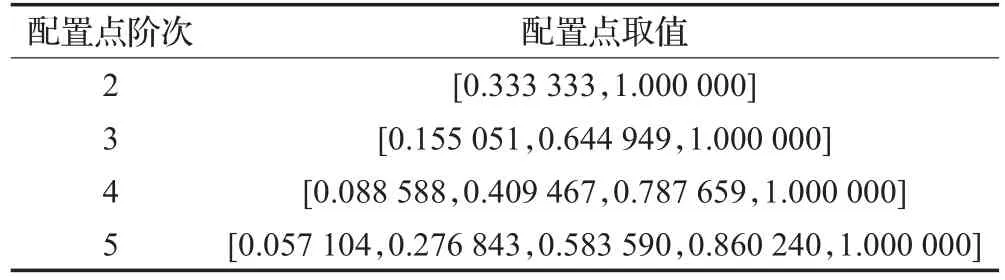
表3 radau配置點取值

設定有限元個數nκ=2，配置點階次nθ分別取2、3、4進行實驗仿真，由于模型參數的不確定性，在ΔHrealR=(0.7,1.0,1.3)×ΔHR分別與 kreal0=(0.7,1.0,1.3)×k0組合得到的9種可能情況下進行實驗，分別得到批次反應時間和求解一次優化問題的平均時間，并以箱線圖的形式畫出，如圖3、4。從圖3中可以看出，隨著nθ的增加，批次反應時間有減少的趨勢，這符合目標方程的設定。可見nθ在一定范圍內增加可以通過更好地逼近真實曲線而帶來更好的控制效果。而從圖4反應出，隨著nθ的增加，在反應過程中，在每個采樣時間求解最優化問題所需的平均運算時間也大幅度地增加，以中位數為例，nθ=2時，中位數為2.1 s，而在 nθ=3,4 時，這一數值分別達到了6.5 s和26.2 s。故雖然配點階次增加可以帶來控制效果的略微提升，但由于過度地增加了優化問題的計算時間使得不符合實際過程控制的實時性要求。

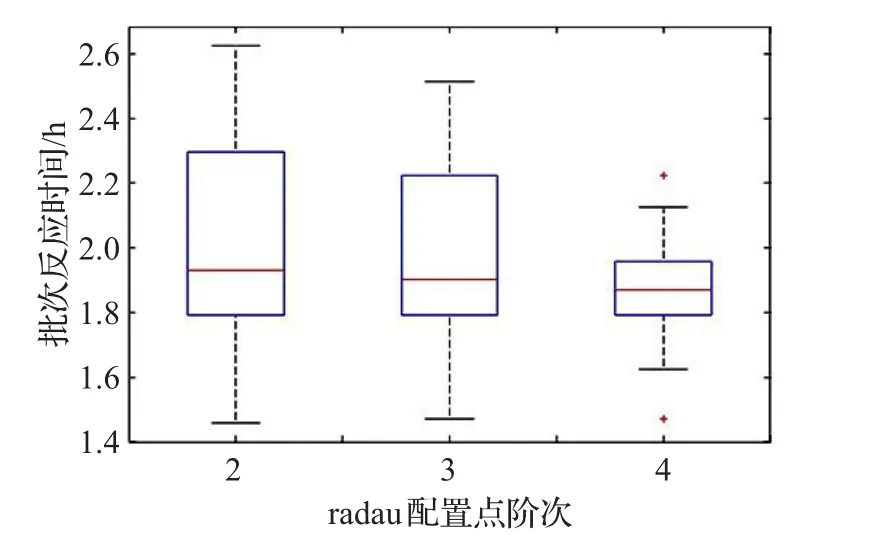
圖3 radau配置點階次為2、3、4時，一個批次反應所需時間

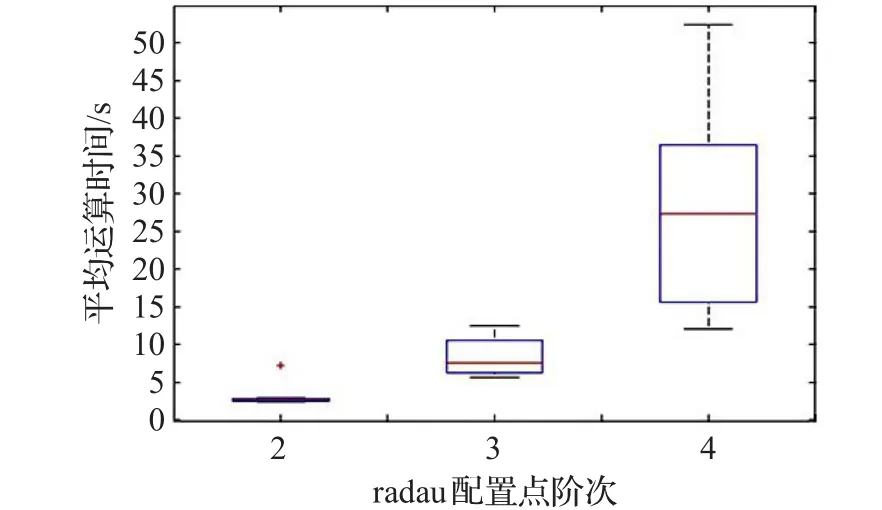
圖4 radau配置點階次為2、3、4時，求解一次優化問題平均時間

5.2 控制效果分析

根據5.1節實驗結果，設定nκ=2，nθ=2，分別采用直接radau配置的Multi-stage NMPC（以下簡稱為RMSNMPC）和傳統NMPC對模型進行仿真，模型參數設置如5.1節。在9種參數組合中有3種情況NMPC無法完成一個批次的反應，故不作圖分析。其他仿真結果如圖5～9，圖中的紅線表示溫限。從圖中可以看出，在任意一個情形下，RMSNMPC均可以較好地完成一個批次的反應，釜溫不僅被控制在安全溫度以內，也被控制在(363.15±2.0)K精度范圍內。而NMPC在多數情形下，如圖6、7、9，反應釜釜溫都沒有達到要求的控制精度要求。更為嚴重的是，在 ΔHrealR=1.0×ΔHR，kreal0=1.3×k0的情況下，如圖7，反應進行到60 min時，處于進料階段，釜溫一度超過了安全溫度，這會給實際生產過程帶來嚴重的安全隱患。此外，雖然NMPC在標稱情況和 ΔHrealR=0.7×ΔHR，kreal0=1.3×k0的情況下可以達到溫度的精度和安全要求，但是進料量都有劇烈震蕩的現象發生，這會給實際控制帶來操作難度。相比之下，RMSNMPC在各個情形下都可以帶來更加平滑的控制量。可見相比于傳統的NMPC，RMSNMPC利用場景樹模擬不確定量的優勢，可以很好地處理具有不確定參數的模型。

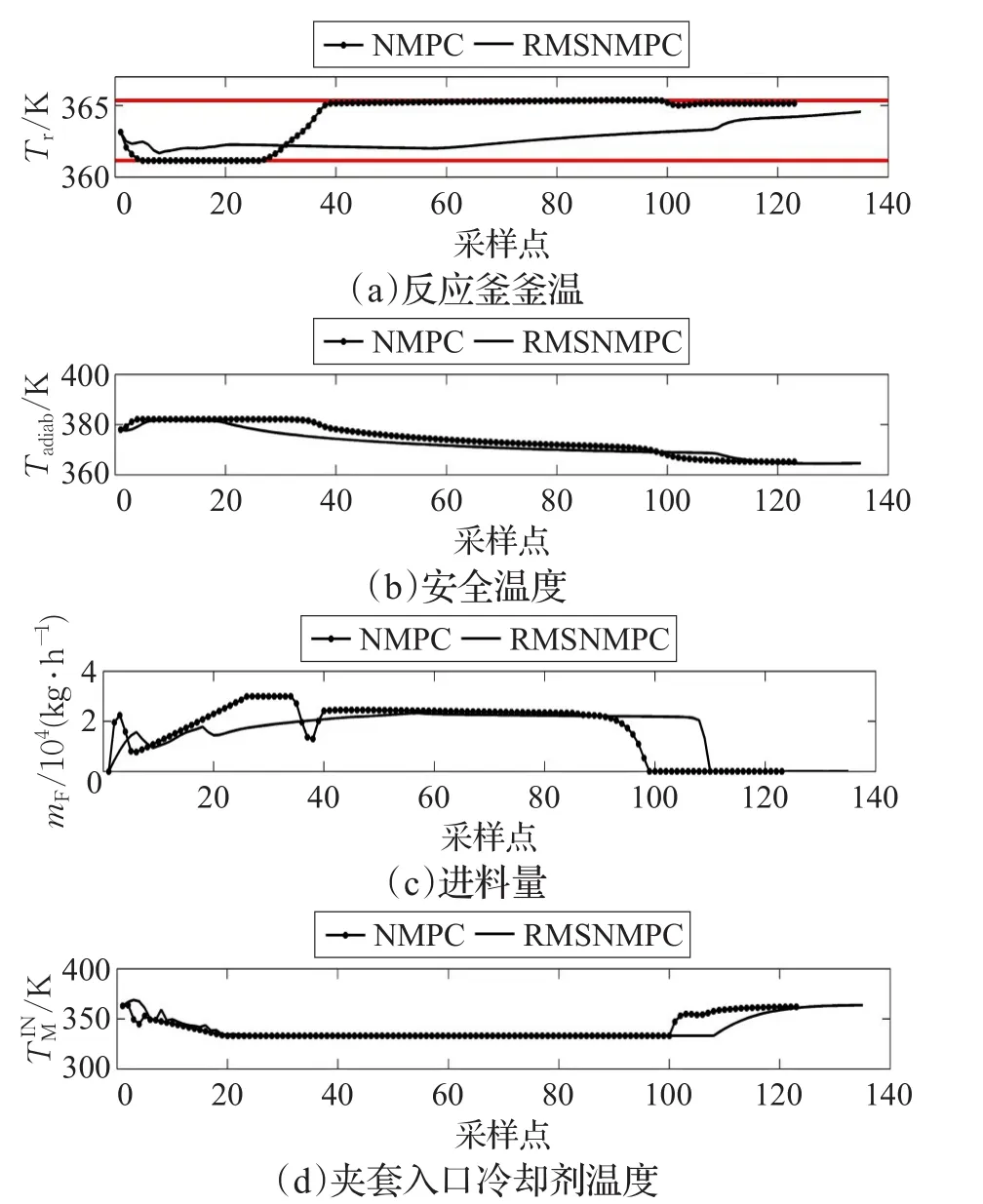
圖5 =1.0×ΔHR，=1.0×k0時，釜溫、安全溫度、進料量、夾套入口冷卻劑溫度曲線圖

圖6 =1.0×ΔHR，=1.3×k0時，釜溫、安全溫度、進料量、夾套入口冷卻劑溫度曲線圖

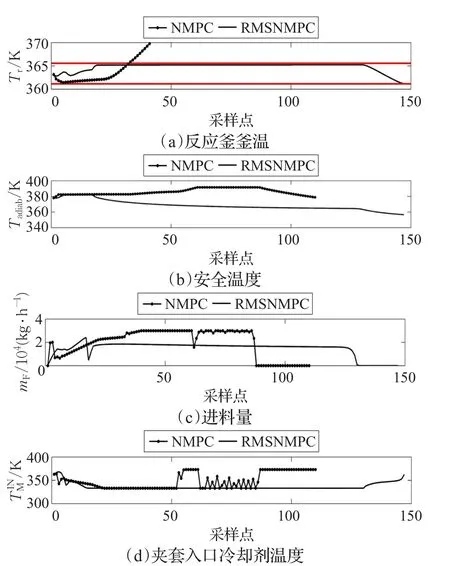
圖7 =1.3×ΔHR，=1.0×k0時，釜溫、安全溫度、進料量、夾套入口冷卻劑溫度曲線圖

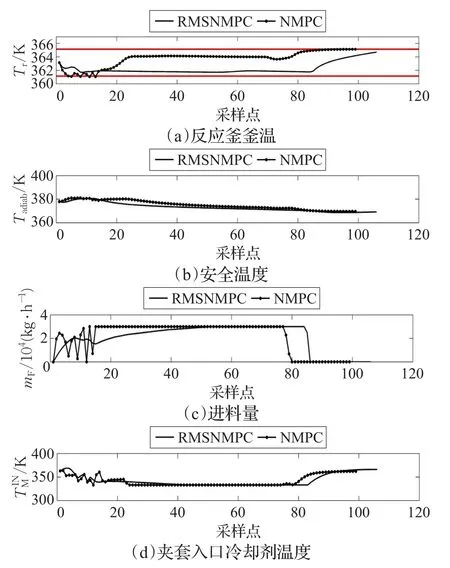
圖8 =0.7×ΔHR，=1.3×k0時，釜溫、安全溫度、進料量、夾套入口冷卻劑溫度曲線圖

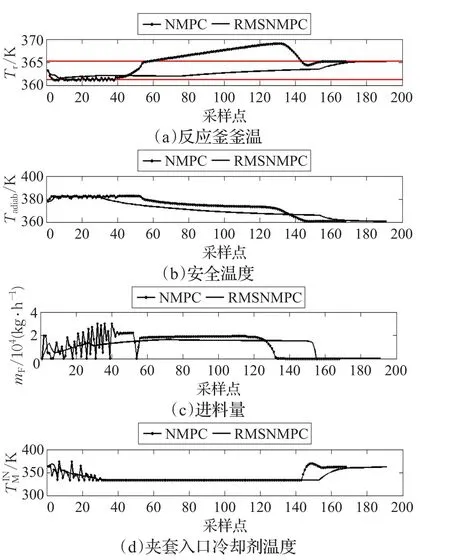
圖9 =1.3×ΔHR=0.7×k0時，釜溫、安全溫度、進料量、夾套入口冷卻劑溫度曲線圖

6 結束語

針對半間歇聚合反應模型中存在不確定參數的情況，基于場景樹模擬不確定量的Multi-stage NMPC方法，提出使用基于有限元正交配置的聯立法對優化問題進行求解。通過大量實驗選取最佳的radau配置點，形成有效的RMSNMPC方法。仿真結果表明在標稱模型和具有不確定參數的模型下，所采用的算法不僅能使反應滿足被控的溫度精度要求和安全要求，還具備良好實時求解能力和魯棒性。相比于傳統的NMPC算法，更適用于復雜的半間歇聚合反應的控制。

[1]Wang J，Wang Y，Cao L，et al.Adaptive interative learning control based on unfalsified strategy for Chylla-Haase reactor[J].IEEE/CAA Journal of Automatica Sinica，2014，1（4）：347-360.

[2]Jang H，Lee J H，Biegler L T.A robust NMPC scheme for semi-batch polymerization reactors[J].IFAC-Papers on Line，2016，49（7）：37-42.

[3]何德峰，丁寶蒼，于樹友.非線性系統模型預測控制若干基本特點與主題回顧[J].控制理論與應用，2013，30（3）：273-287.

[4]Idris E A N，Engell S.Economics-based NMPC strategies for the operation and control of a continuous catalytic distillation process[J].Journal of Process Control，2012，22（10）：1832-1843.

[5]Campo P J，Morari M.Robust model predictive control[C]//American Control Conference，1987：1021-1026.

[6]Lee J H，Yu Z.Worst-case formulations of model predictive control for systems with bounded parameters[J].Automatica，1997，33（5）：763-781.

[7]Mayne D Q，Kerrigan E C，Van Wyk E J，et al.Tube based robust nonlinear model predictive control[J].International Journal of Robust and Nonlinear Control，2011，21（11）：1341-1353.

[8]Lucia S，Finkler T，Engell S.Multi-stage nonlinear model predictive control applied to a semi-batch polymerization reactor under uncertainty[J].Journal of Process Control，2013，23（9）：1306-1319.

[9]Lucia S，Engell S.Multi-stage and two-stage robust nonlinear model predictive control[C]//Nonlinear Model Predictive Control，2012，4（1）：181-186.

[10]陳楊，邵之江，錢積新，等.聯立法中全局和局部正交配置算法[J].化工學報，2010（2）：384-391.

[11]黃森.動態優化問題的移動有限元算法研究[D].杭州：浙江大學，2012.

[12]Canuto C，Hussaini M Y，Quarteroni A M，et al.Spectral methods in fluid dynamics[M].New York：Springerverlay，2012.

[13]Biegler L T.An overview of simultaneous strategies for dynamic optimization[J].Chemical Engineering and Processing：Process Intensification，2007，46（11）：1043-1053.

[14]Ascher U M，Petzold L R.Computer methods for ordinary differential equations and differential-algebraic equations[M].Philadephia，PA，USA：SIAM，1998.

[15]陳楊.基于微分—代數混合方程機理模型的非線性預測控制[D].杭州：浙江大學，2011.