基于聚類的流面自動布局及生成算法

唐 燁，解利軍，桂立業，何麗莎，鄭 耀

浙江大學 航空航天學院，杭州 310027

1 引言

流場可視化是科學可視化的經典分支之一。通過直觀的圖像來表示抽象的流場數據[1]，既可以加快從數據中獲取信息的速度，又能讓不具備領域專業知識的人理解這些信息。如今在航空航天、氣象、自動化等領域的科學研究過程中，流場可視化已經成為不可或缺的技術。

流面可視化是流場可視化的一種方式，近幾年來越來越流行[2]，相比于常用的流線法，流面法更適合表現復雜的流場結構[3]，并且展現更豐富的流場局部信息[4]。

1.1 相關概念

流場是一種矢量場。在空間坐標系(x,y,z)中，任意點(x0,y0,z0)都有唯一確定的向量(Vx,Vy,Vz)與之對應，就說在空間(x,y,z)范圍內存在矢量場V。在流場中，該矢量場即速度場。

流線是一個無質量的質點（種子點）在某一穩定流場中以某點為起點，在該流場中運行的軌跡。流線上的每一點都與流場中該點對應的速度相切。假設V(x)是一個三維向量場，在時刻t經過點x0的流線為L(x0,t)，其中L(x0,t)滿足公式（1）：

類似于流線的概念，流面是某條種子線C的所有種子點以C中的位置為起點在穩定流場中運行的軌跡的集合，設該流面為S，S滿足公式（2），流面S中的點處處與流場中該點處的速度相切[5]。

其中S(s,t)是種子點C中s處的種子點在流場中的運動軌跡，也就是由C中s處的種子點生成的流線，S為C中所有點生成的流線的集合，如圖1所示。

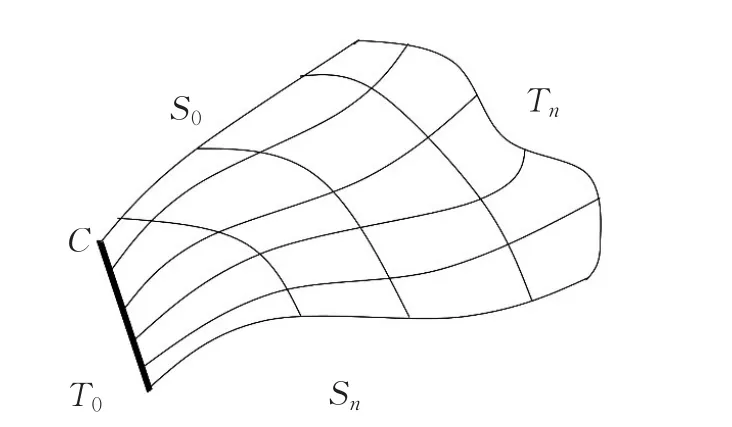
圖1 流面示意圖

1.2 相關工作

Hultquist首先在1992年提出了一種高效的流面生成算法——前沿推進算法。……