從幾道小學測試題看“數形結合”思想的培養

◎毛鴻雁

筆者近期接觸到幾道小學五年級的測試題，深刻體會到小學是培養學生“幾何直觀”的一個很重要的時期，很多復雜問題都要通過“數形結合”來幫助理解從而達到簡化效果，具體可以通過作“線段圖”化抽象為直觀、化復雜為簡單，可以說“線段圖”是學生最早接觸的“數形結合”的一種。在此，簡單舉幾個例子說明。

1：今年爸爸48歲，哥哥的年齡是弟弟的2倍，當弟弟長到哥哥現在的年齡時，爸爸的年齡恰好是兄弟倆的和，請問今年弟弟多少歲？

分析：此題放在五年級測試卷中，主要考查學生通過列簡單方程解決問題的能力。學生解決問題的難點是：由于題目條件中涉及的量有點多且抽象，導致學生理不清題意中的各個量之間的聯系，很難根據題意直接列出方程。此時若借助“線段圖”整理其中的數量關系，就讓數量關系變得直觀、簡明！（如圖）

假設弟弟今年x歲，不難理解，“當弟弟長到哥哥現在的年齡”是指經過年后，所以根據題意可以列方程：48＋x＝2x＋3x，從而解決問題。

2：有兄弟兩人，哥哥對弟弟說：“我在你這么大時，你才1歲！”弟弟對哥哥說：“我到你這么大時，你已經31歲了！”問，兄弟倆各多少歲？

分析：這是一個推理題，學生解決這個問題遇到的難點是題中的未知量很多，弟弟現在多大？哥哥現在多大？弟弟到哥哥那么大時是多少年后？哥哥在弟弟那么小時又是多少年前？就現有的兩個已知量之間很難找到相等關系，會讓很多學生覺得無從下手！但是，一旦我們作出線段圖將數量關系整理出來，就會輕松理清數量間的關系，容易發現在這個問題中最關鍵的量是年齡差。（如圖）

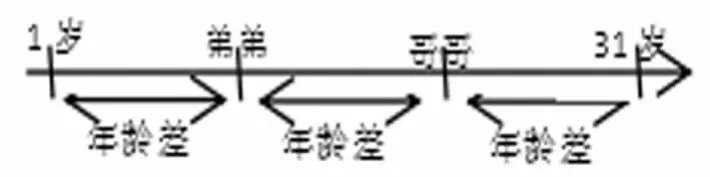
設兄弟間年齡差為x歲，則根據題意可以列出方程：3x＝31-1，從而解決問題。

3：請用數學思維解決問題：

三人同時從工廠乘出租車回家，事先講好三人分擔車費，丙最后到達終點付車費90元，已知甲到了全程的處下了車，乙在全程的處下了車。問甲乙分別應付給丙多少車費錢？

分析：這個題相對比較開放，題目中沒有說清楚三人按什么方式分擔車費。

思路一：如果簡單粗暴的解決問題，三人平均分攤車費，那么90÷3＝30元/人。而這樣的分配車費方式顯然不合理，畢竟每人乘坐出租車的路程不一樣。

思路二：如果按照每人乘坐出租車的路程比例來看這個問題，甲乘坐的路程占全程的、乙乘坐的路程占全程的、丙乘坐的路程占了全程的1。所以可以將全程分成2份，其中甲占了份，乙占了份，丙占了1份。也就是如果把車費看成“1”的話，甲應該付總車費的÷2＝，同理乙應該付總車費的，而丙則應該付總車費的。（如圖）

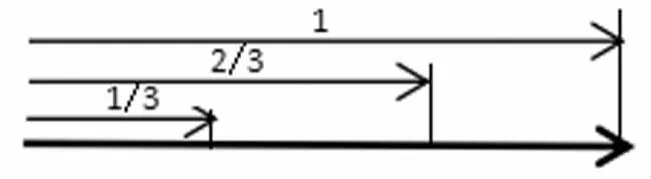
所以甲付15元車費，乙付30元車費，丙則實際付45元車費。

思路三：如果按照出租車實際行駛路程產生的費用來分攤，我們可以把90元車費看作是三段路程的車費總和，每一段車費30元。第一段路程3人平均分攤，每人10元；第二段路程2人平均分攤，每人15元；第三段丙一人承擔30元。（如圖）

所以，甲付10元車費，乙付25元車費，丙則實際付55元車費。

通過幾個例子我們體會到，“數形結合”能啟迪思路，幫助理解。我國數學家華羅庚先生就曾經說過：“數缺形時少直觀，形少數時難入微。數形結合百般好，隔離分家萬事休。”因此在教學中，要引導和鼓勵學生借助幾何直觀進行思考，揭示研究對象的性質和關系，從而滲透“數形結合”的數學思想。