基于ARIMA模型的電子銀行交易時序預測

林其經 魏凌

【摘要】文本以成都市某電子銀行交易數據為樣本，進行時間序列分析。基于R軟件采用ARIMA時間序列模型對交易數據進行擬合，并通過分析殘差序列檢驗模型擬合的準確性，在此基礎上對未來交易數據走勢進行了預測。

【關鍵詞】電子銀行；ARIMA模型；預測

1 電子銀行概述

電子銀行是一種新型的銀行交互式服務方式，使用電子銀行的客戶只需要通過電腦、手機、POS機等終端就可以不用親自去銀行網點從而實現交易。一般來說，電子銀行包括手機銀行，網上銀行等。由于電子銀行的獨有特性，其優越性顯而易見。（1）用戶可以全天候24小時進行電子銀行的交易。（2）用戶可以在任何有網絡的地點下進行電子銀行交易。（3）用戶可以更加規范和程序化的進行金融交易。

筆者通過走訪成都市某大型商業銀行，獲取了從2017年11月13日至2017年11月19日這7天并以分鐘計提的交易數據。由于所獲取數據屬時間序列數據，因此本文嘗試采用ARIMA模型對該交易數據進行擬合，并對未來數據走勢進行預測。

2 數據描述與處理

通過篩選缺失數據及無效數據共獲得有效數據10055個。

由于該數據有很強的波動性和周期性，因此需要對該數據進行差分處理。

對原始數據進行二次差分處理可以得到差分后的數據，為了驗證差分后的數據的平穩性可以對其進行單位根平穩性檢驗（ADF檢驗），檢驗結果如下表1所示：

通過表1可以看出，ADF檢驗P值為0.01，小于一般情況下所給定的顯著性水平（α=0.05），可以認為二次差分后的數據是平穩的。

3 模型識別與檢驗

為了驗證該序列所屬模型，對差分后的數據采用自相關函數圖（ACF）和偏自相關函數圖（PACF）進行分析。

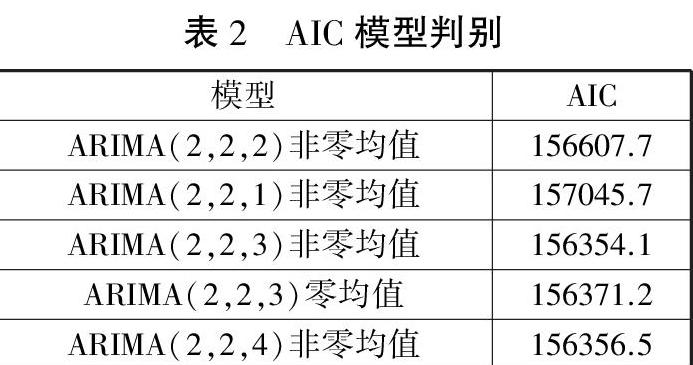
通過結果可以看出時間序列的自相關圖和偏自相關圖都呈現拖尾的情況，并且自相關系數在二階后明顯收斂但偏自相關系數不好判定，所以可以認定模型屬于 ARIMA（2，2，q）模型，確定q的參數則需要通過AIC準則進行判斷。

遵從AIC最小準則，可以推斷出最適合的模型為非零均值的ARIMA（2，2，3）。并且利用矩估計的方法可以得到該模型的參數估計值，因此擬合ARIMA（2，2，3）模型的方程（1）如下。

Xt=0.8021Xt-1-0.0268Xt-2+εt-2.4135εt-1+1.9041εt-2-0.4888εt-3（1）

為了判斷所識別的模型正確與否，需要對該模型進行檢驗。由于模型ARIMA（2，2，3）的識別與估計是在假設隨機干擾項εt是一個白噪聲的基礎上進行的，因此，如果模型確認正確的話，殘差εt代表的是一個白噪聲序列。這里采用QLB統計量進行χ2檢驗，檢驗結果如表3所示。

由QLB統計量所計算出的χ2值所屬P值為0.9901，大于一般性顯著性水平（α=0.05），而接受統計量的原假設（HO：殘差序列是白噪聲序列），故擬合的模型通過QLB統計量的殘差序列檢驗。

4 模型的預測與分析

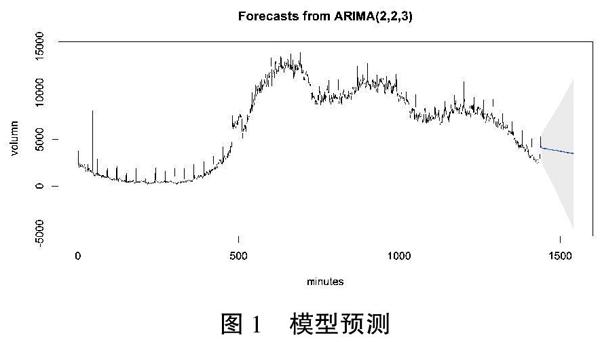
為檢驗模型的預測效果，用擬合出的ARIMA（2，2，3）模型對2017年11月20日前100分鐘的數據進行預測，結果如圖1所示。

圖1展示了2017年11月19日的交易數據以及2017年11月20日前100分鐘的預測數據，其中末尾的藍色線條即預測的交易數據。可以看出預測數據與前一天數據的前100分鐘數據走勢都呈現下行趨勢。由于交易數據表現出強烈的周期性，因此有理由推斷該預測的交易數據與上周同一時刻的交易數據會呈現出相似性。

5 結論

從以上的分析結果可以得出以下兩點結論。

（1）本文數據所建立的ARIMA （2，2，3）模型可以很好的通過殘差序列檢驗，因此該模型可以很好的擬合交易數據。

（2）將該模型對未來100分鐘的交易數據進行預測，發現該模型可以較好的擬合未來交易數據的大體趨勢以及均值水平。但是對于短期交易數據的精確把握較為匱乏，需進一步改善。

參考文獻：

[1]程鑫.透過電子銀行交易數據分析銀行發展現狀[J].新財經：理論版，2012（4）

[2]梁環忠.我國商業銀行電子銀行營銷攻略的幾點思考[J].河北金融，2012（4）