基于不定核LS-SVM模型的公司違約概率預測

李 昊，梁 州，黃 迅，林 宇（教授）

一、引言

近年來，我國債券市場實現了大幅度的跨越式發展，2016年全年發行債券35.6萬億元，同比增長56.1%，各類債券余額同比增長30.7%，達到了63.8萬億元，約占GDP比重的85.7%。然而，在債券市場迅猛發展之際，受過度投資、缺乏有效風險管理、信息不對稱、投機氛圍濃厚等復雜因素的綜合影響，自2014年“11超日債”違約開始，“15五洋債”“15機床MTN001”等眾多公司違約事件近年來不斷涌現[1]。這不僅擾亂了我國債券市場的既定秩序，給投資者帶來嚴重損失，甚至還可能誘發系統性風險，阻礙整個經濟社會的健康發展。因此，科學開展對我國債券市場公司違約概率的預測研究，對于公司經營者以及監管層防范和化解風險與危機具有重大而深遠的意義。

相當長時期以來，學術界與實務界已不遺余力地開發出Credit Risk+、邏輯（Logistic）回歸、概率比（Probit）回歸、KMV、人工神經網絡（Artifical Neural Network，ANN）等一系列模型對公司的違約概率進行了廣泛而深入的研究[2][3][4][5][6]。雖然相關研究取得了令人滿意的成果，但是上述模型卻都存在前提條件過于苛刻、過學習、局部最小值等問題[7]。令人欣喜的是，支持向量機（Support Vector Machine，SVM）卻正好擁有解決這些問題的突出優勢，使其具有更為優異的泛化推廣能力，從而自其被提出以來，就受到廣大學者的青睞并被廣泛運用于金融領域的研究之中[8]。并且在傳統SVM的基礎上，學者們還進一步研究出具有更高運算速度和更強抗干擾能力的最小二乘SVM（Least Square Support Vector Machine，LS-SVM）對公司違約概率進行預測研究，且取得了較為矚目的研究成果[9]。因此，本文引入LS-SVM模型對公司違約概率進行預測研究，從而為監管部門以及公司管理層防范風險提供合適的操作工具。

對于公司違約概率預測研究的重點在于構建LS-SVM模型，而構建LS-SVM模型的關鍵又在于對核函數（Kernel Function）的選取[10]。雖然目前研究均使用正定核（Positive Kernel）來構建LS-SVM模型[11]，但是基于樣本數據集所構建的正定核矩陣的特征值往往為正，特征值為負的情形從未被納入核矩陣的構建中。隨著經濟一體化與金融全球化的深入推進，各國金融市場間的聯系日益緊密，金融市場數據也呈現出更為復雜的結構特征，從而導致基于金融市場數據集所構建核矩陣的特征值出現負值的情況普遍存在，如果仍然使用正定核對金融市場數據集進行核矩陣的構建，將很可能無法刻畫金融市場數據的復雜結構特征，從而造成構建的LS-SVM模型出現預測偏誤，導致公司違約概率預測研究的失敗[12]。令人欣慰的是，隨著對核函數的深入探索，有部分學者另辟蹊徑，探索出不定核（Indefinite Kernel）這一新穎的核函數構建方法，能夠根據樣本數據集的復雜結構特征自適應地構建特征值或正或負的核矩陣，從而更為有效地提升LS-SVM的預測性能，不定核相較傳統正定核所具有的上述明顯優勢，也在實證研究中獲得了充分的驗證[13]。因此，本文將構建基于不定核的LS-SVM模型，以期為公司的違約概率預測奠定堅實的理論基礎與工具保障。

基于以上分析與認識，本文以短期融資券作為研究對象，以交叉驗證（Cross Validation，CV）作為模型的訓練方法，將傳統正定核LS-SVM模型拓展為不定核LS-SVM模型對公司違約概率開展預測研究，并將不定核LS-SVM模型與其他預測模型進行預測性能的比較研究，進而針對在國民經濟中位于重要地位的違約風險高發行業，對不定核LSSVM模型的穩健性進行考察。

二、文獻綜述

迄今為止，就所掌握的文獻而言，已有學者將LS-SVM模型運用于金融領域進行預測建模。Zhu等[14]將經驗模態分解（Empirical Mode Decomposi?tion，EMD）與LS-SVM模型相結合，提出了EMDLSSVM-ADD模型，并對碳價格進行了預測研究。更進一步地，在LS-SVM模型下運用不定核的研究中，Huang等[15]在LS-SVM模型的框架下，基于UCI訓練集，將不定核與正定核進行對比，實證研究表明，不定核LS-SVM模型在某些UCI數據集下要顯著優越于正定核LS-SVM模型。而在圍繞債券市場公司違約概率的研究中，盡管曹勇等[16]發現將不同行業進行區分以進行公司違約概率的研究可以較大程度地提高Logistic模型的擬合優度，且各行業中影響公司違約概率的財務指標不盡相同。但毋庸置疑的是，上述文獻僅對債券市場公司違約概率進行了測算，而并未進行預測研究。本文不僅將不定核LS-SVM模型引入公司違約概率的預測研究中，還將其與正定核LS-SVM模型以及Logistic模型在整體行業和分行業進行了預測精度比對。由此可見，與已有的文獻相比本文具有明顯的創新性。

三、研究方法

1.基于正定核LS-SVM模型的公司違約概率的預測方法。對于債券市場來說，用狀態變量刻畫在t時刻的起息日期下，第i只短期融資券的違約概率，其中i=1，2，…，n。用 來刻畫短期融資券的特征變量，其中d表示特征變量對應的維度，d=1，2，…，m。因為本文研究的是公司違約概率的預測方法，即：通過運用當期的特征變量來預測下一期的狀態變量，所以各研究樣本可以構造為，表示運用t時刻短期融資券的特征變量來預測t+1時刻的違約概率。

利用LS-SVM模型進行公司違約概率預測的優化目標為：

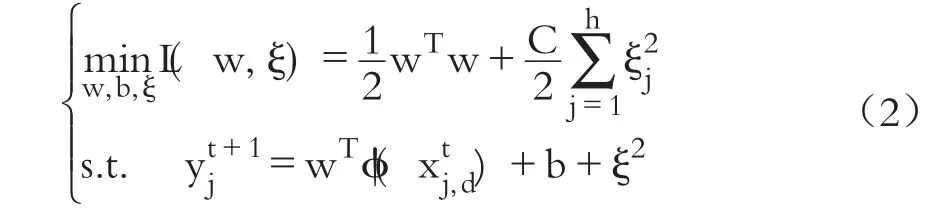
式中：ξj為非負的松弛變量；C/2為給定的正則化參數。同時，為了求解上述優化問題便要引入拉格朗日乘數，將其變成無約束優化問題：

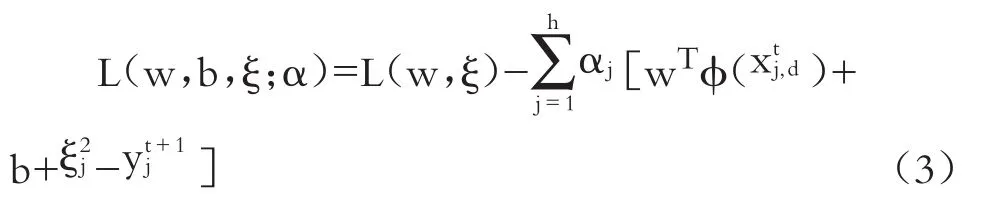
式中：αj為拉格朗日乘子。

根據KKT最優化條件，有：

消去w和ξj，可得到：

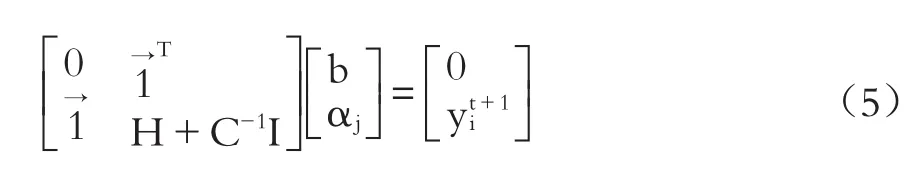
進而將由式（5）求出的αj和b代入違約概率預測模型，即可得到最終的函數表達式：

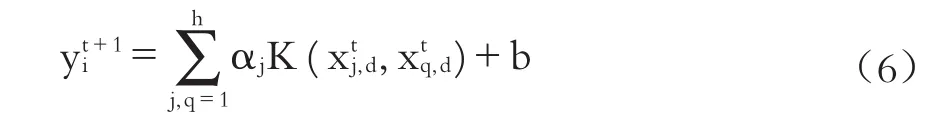
本文采用目前研究廣泛使用的徑向基核函數（Radical Basis Function，RBF）、多 項式核 函 數（Polynomial Kernel）、線性核函數（Linear Function）以及Sigmoid核作為所采用的正定核，其表達式如下：

RBF核：

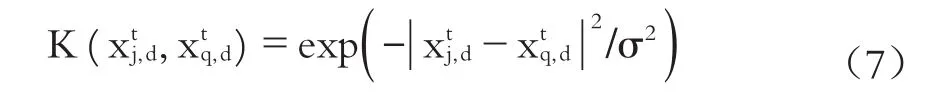
Poly核：

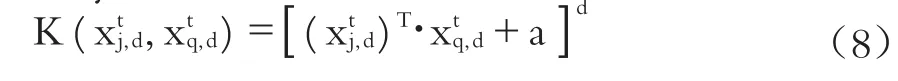
Linear核：

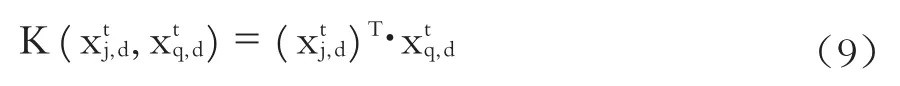
Sigmoid核：

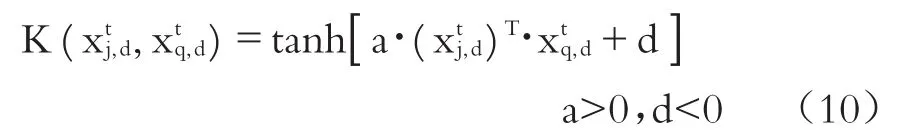
至此，基于正定核LS-SVM模型的公司違約概率預測模型就已構建完畢，但正如前文所述，面對日益復雜的金融數據結構，倘若使用核矩陣特征值僅能為正的正定核，勢必導致LS-SVM模型的預測結果陷入一個局部值，而忽略當特征值出現負數情形下最優值的選擇，且限制了核函數的構建形式以及縮小了核函數的選擇空間，于公司違約概率預測不利。因此，下文將重點構建不定核LS-SVM模型，以提高LS-SVM公司違約概率預測模型的預測精度。

2.基于不定核LS-SVM模型的公司違約概率的預測方法。為使用LS-SVM模型對公司違約概率進行準確預測，需對核函數進行有效的選擇，下面本文將引入不定核對違約概率進行建模分析。

通常而言，為運用不定核，需從再生核Krein空間（Reproducing Kernel Krein Space，RKKS）出發，倘若存在，那么對于任意給定的短期融資券樣本訓練集而言，不定核存在如下分解：

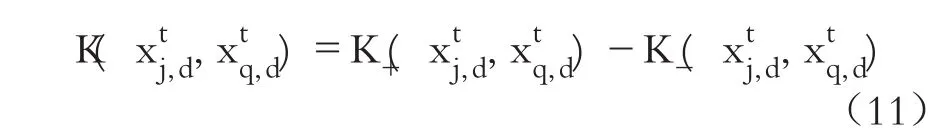
由此，不定核可由正定核進行線性組合得到，LS-SVM模型所進行的不定學習在RKKS中也與再生核 Hilbert空間（Reproducing Kernel Hilbert Space，RKHS）不謀而合，也正因如此，該模型所進行的不定學習得到了理論支持。相較于正定核而言，不定核能夠根據公司違約概率樣本數據集的復雜結構特征自適應地構建特征值或正或負的核矩陣，從而能更適用于LS-SVM模型的建模分析，對于公司經營者以及監管當局而言意義重大而深遠。

進而相較于正定核公司違約概率預測模型即式（6）而言，基于不定核LS-SVM模型的公司違約概率有著如下形式：

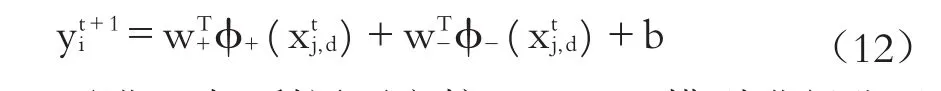
更進一步，利用不定核LS-SVM模型進行公司違約概率預測的優化目標由式（2）轉換為：

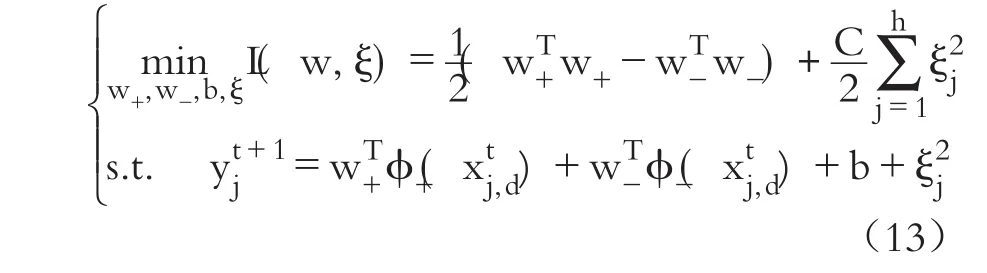
從而，所求解的無約束問題變為：

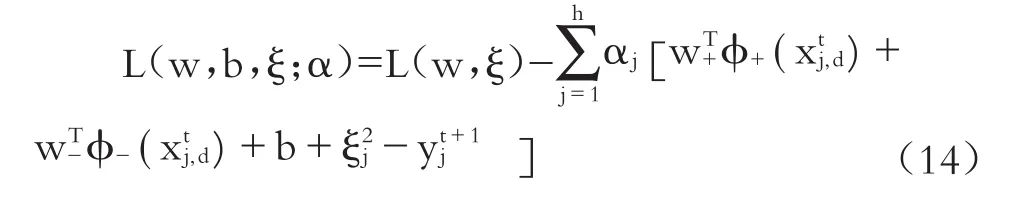
而其穩定點條件為：

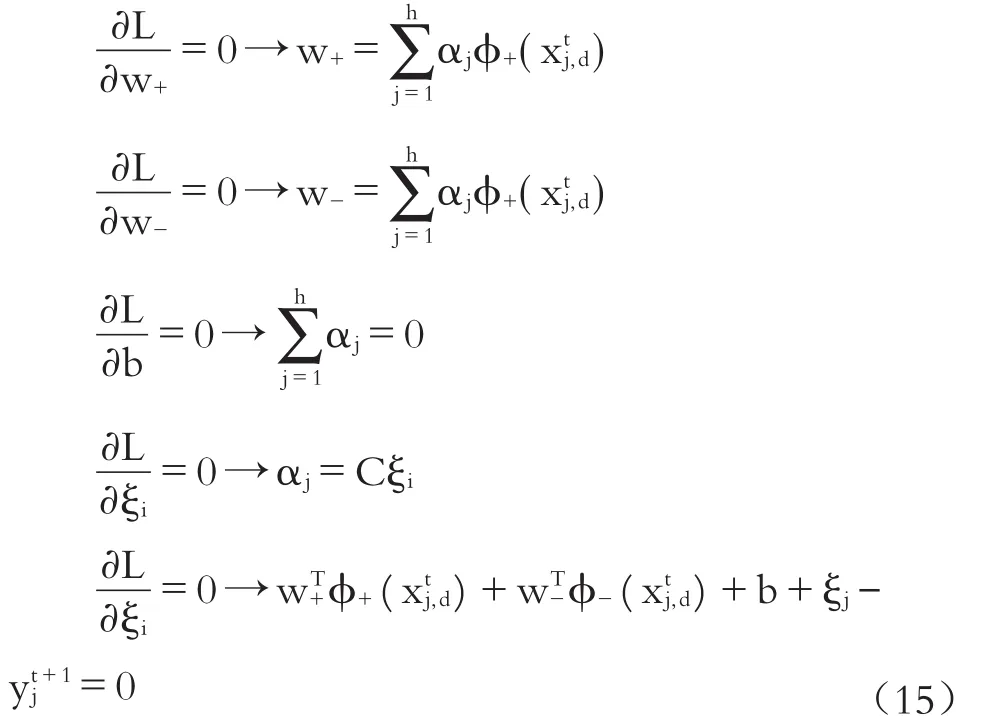
消去w+、w-、ξj，可得到：

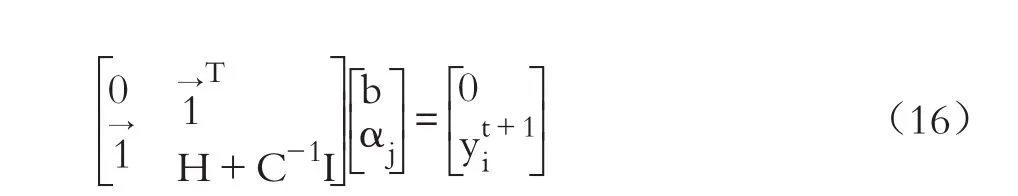
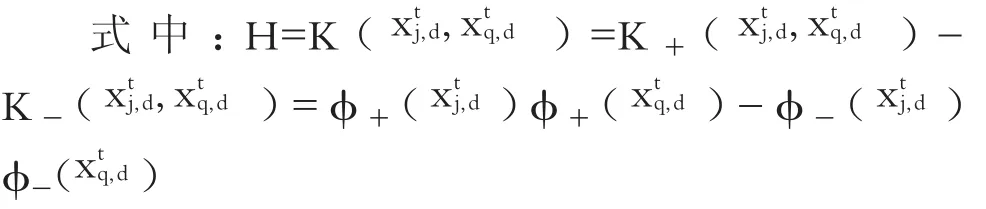
將式（16）求出的αj和b代入式（12）即可得出基于不定核LS-SVM模型的公司違約概率預測模型：

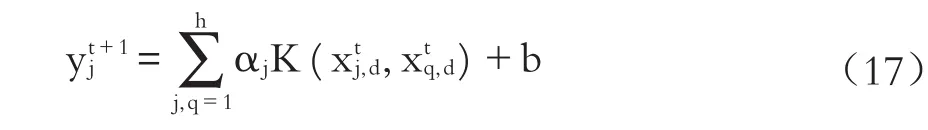
由于大量文獻采用Sigmoid核函數作為不定核[12][15]，所以本文采用Sigmoid核函數作為不定核LS-SVM模型的核函數：

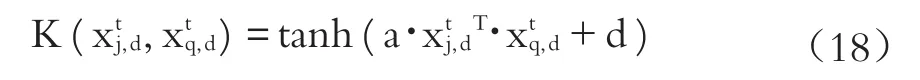
在此需要進一步強調的是，根據Lin等[17]的研究成果，當a＞0、d＜0時，Sigmoid核函數被認為是正定核；而除此之外，Sigmoid核函數被認為是不定核。可以看出對于不定核的Sigmoid核函數而言，避免了因參數取值范圍受到限制而陷入局部最小值的情況，進而引入不定核Sigmoid核能夠使得Sigmoid核函數更適合應用于公司違約概率現實預測研究。

至此，基于不定核LS-SVM模型的公司違約概率預測模型構建完成。

3.基于信用利差的違約概率測算。要想合理地預測公司的違約概率，不僅要構建合理的違約概率預測模型，更關鍵的是要對違約概率進行精確的測算。一般來說，一單位短期融資券的價格應該保證其期望收益率至少等于一單位無風險投資的收益率[18]：

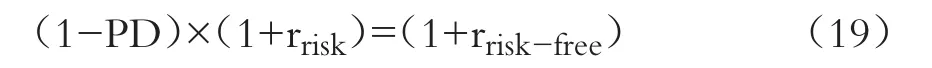
式中：PD表示違約概率；rrisk表示短期融資券的利率；rrisk-free表示無風險利率。

將式（19）整理得到：

眾所周知，短期融資券的信用利差（Cost Spreads，CS）由其發行利率與無風險利率之差來衡量，從而式（20）可表示為：

只有準確地計算信用利差，才能對公司的違約概率進行有效的測算。本文將國債利率作為無風險利率，并利用牛頓插值法補填了公司債券發行當天所缺少的國債利率樣本。因此，本文將根據式（21）對短期融資券的違約概率進行測算，為預測工作的進一步展開奠定良好的基石。

4.公司違約概率預測模型的性能評價指標。對預測結果的精度評價是短期融資券違約概率預測中較關鍵的部分。為了評價預測模型的性能，本文將運用均方根誤差（Root Mean Square Error，RMSE）、平均絕對百分比誤差（Mean Absolute Percentage Error，MAPE）和平均絕對誤差（Mean Absolute Error，MAE）來對預測模型的準確性進行分析與評價。

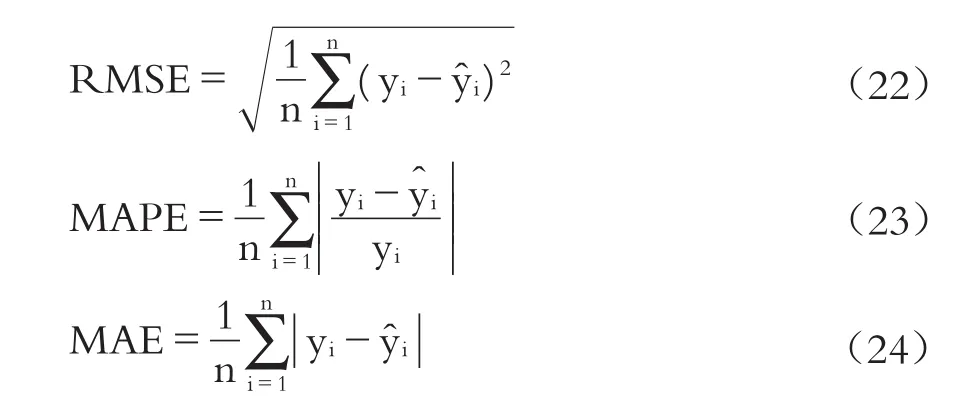
其中，RMSE和MAE用來衡量模型的整體預測能力。RMSE和MAE越小，則模型預測精度越高，反之亦然。而MAPE衡量了模型的局部預測能力，其值越小，則模型的預測精度越高，反之則反。

四、實證檢驗與結果分析

1.樣本選擇。考慮到2006年企業會計準則的頒布及2008年金融危機對于債券市場的影響，本文以起息時間為2008年1月10日的短期融資券為研究對象，并按照如下標準對樣本進行篩選：①對同一會計年度內發行超過一期短期融資券的上市公司，本文隨機地保留一個樣本。②因城投債發行動機與本文研究不符，剔除城投債性質的短期融資券。③因需計算信用利差，僅保留固定利率短期融資券，且本文主要考察平價發行的債券，故剔除貼現式債券。④剔除金融類公司。⑤剔除樣本缺失的短期融資券。共計得到3238個樣本，數據來源于Wind數據庫，其中短期國債數據來源于中國債券信息網，部分短期國債數據利用牛頓插值法進行了構造。為避免極端值的影響，本文對財務數據進行了上下1%分位上的縮尾（Winsorize）處理。

2.特征指標變量的篩選。要想合理地構建公司違約概率預測模型，前提在于對公司違約概率的影響因素進行有效的篩選，因此，本文通過借鑒陳詩一[19]、曹勇等[16]的研究，從流動性、運營能力、盈利能力和資本結構這4個方面挑選出22項財務指標，同時挑選出4項具有代表性的公司非財務指標（模型的特征指標見表1）。

表1 公司違約概率預測模型的特征指標

為避免特征指標維數過高導致模型的“過擬合”，也為保證特征指標存在顯著差異以使得模型的效果最優，本文將參考遲國泰等[20]的研究，運用偏相關分析對相關系數大于0.8的指標進行篩選以剔除模型中的冗余信息，但偏相關系數（兩兩之間）是兩兩之間的系數，究竟刪除其中哪個特征指標還應該具體考慮。本文在找到偏相關系數（兩兩之間）大于0.8的7組特征指標后，為保證實驗的客觀開展，首先將偏相關系數（兩兩之間）大于0.8中多次出現的特征指標予以刪除，如表2中的速動比率、總資產報酬率以及息稅前利潤率；然后，剔除了偏相關系數（平均數）較大的Log（總資產）；最后，無論對于公司管理層還是對于監管部門來說，在公司發生違約且面臨破產時，均更關注以所有者權益與總資產比值衡量的本金比率，從而本文剔除違約距離。因此，本文將選擇除速動比率、總資產報酬率、息稅前利潤率、違約距離以及Log（總資產）以外的特征指標進行公司違約概率預測模型的建模分析，以期為公司管理層以及監管當局提供優秀的操作工具。

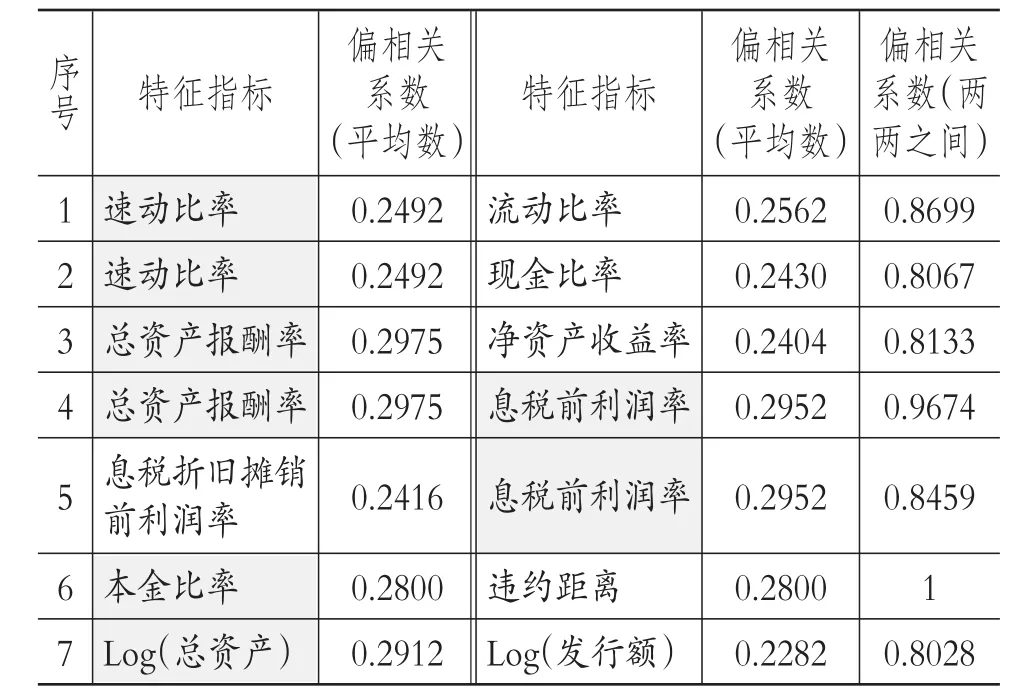
表2 偏相關系數（兩兩之間）大于0.8的指標

3.不定核LS-SVM模型與其他預測模型的性能對比。由于學者們普遍使用Logistic模型進行違約概率的研究[21]，因此，本文僅將不定核LS-SVM模型與除正定核LS-SVM模型以外的Logistic模型進行違約概率預測精度對比。與此同時，為了避免人為劃分樣本造成預測模型獲得的實證結果存在隨機性，本文采用交叉驗證方法對不定核LS-SVM模型、正定核LS-SVM模型以及Logistic模型進行試驗訓練，即：將樣本數據集隨機劃分為10份，令其中1份為測試集，另外9份為訓練集，然后基于訓練集進行實證建模，從而獲得10次結果并取其平均值，結果見表3。值得一提的是，為預測公司違約概率，應選擇t-1時期的特征指標，但由于債券發行時期有可能小于公司上年度財務報表發布的時期，如果繼續使用t-1時期的特征指標則不符合實際的情形。因此，當出現此種標準時，本文以t-2時期的特征指標代替t-1時期的特征指標，也因此本文所預測的違約概率與實際情形更相符。本文在MATLAB 2016a的編程環境下進行實證分析，對于LS-SVM模型主要依靠LS-SVMlab這一通用工具包實現。

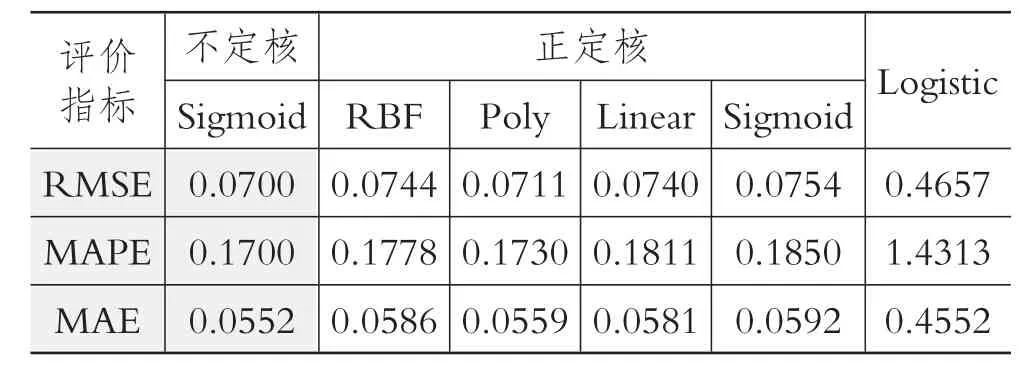
表3 不同模型違約概率預測精度的對比

從表3中可以很清晰地看出，較正定核LSSVM模型以及Logistic模型來說，不定核LS-SVM模型在RMSE、MAPE以及MAE上均獲得最小值。因此，從預測的精度上看，不定核的引入能夠較大地提升LS-SVM的預測性能，在公司違約概率的預測上具有明顯的優勢。

但是，僅根據整體行業就斷定不定核LS-SVM模型的預測性能最好，不僅缺少對于公司違約概率預測模型泛化性能的驗證，而且整體行業所獲得的結果是否也能推廣至分行業中還缺乏客觀的評價，因此，還要考察不定核LS-SVM模型在分行業中的應用效果才能對其預測性能進行評價。考慮到煤炭、鋼鐵、有色金屬、交通運輸以及食品飲料等行業不僅是國民經濟中的重要組成部分[22]，而且根據劉再杰等[23]的研究，這五大行業也是信用風險較突出的行業，因此進一步本文將針對這五大行業進行不定核LS-SVM模型與其余預測模型的分行業性能對比，以考察該模型的實際應用價值。各模型性能對比結果見表4。

從表4中可以很清晰地看出，不定核LS-SVM模型除在鋼鐵行業中RMSE大于RBF核LS-SVM模型外，在其余各行業的預測中，所得到的各項評價指標均為最小值，且較整體行業而言，在分行業中使用交叉驗證所得到的各評價指標，絕大多數都小于相應的整體行業評價指標值：0.0700、0.1700以及0.0552。以上結果表明，不定核LS-SVM模型的泛化性能極其優越。

五、結論

為了預測公司違約概率，本文以短期融資券為研究對象，構建了基于信用利差的違約概率樣本，進而運用RMSE、MAPE和MAE對不定核LS-SVM模型、正定核LS-SVM模型和Logistic模型進行預測精度的對比，然后為了檢驗模型的穩健性，進行了分行業中各預測模型的預測精度對比。

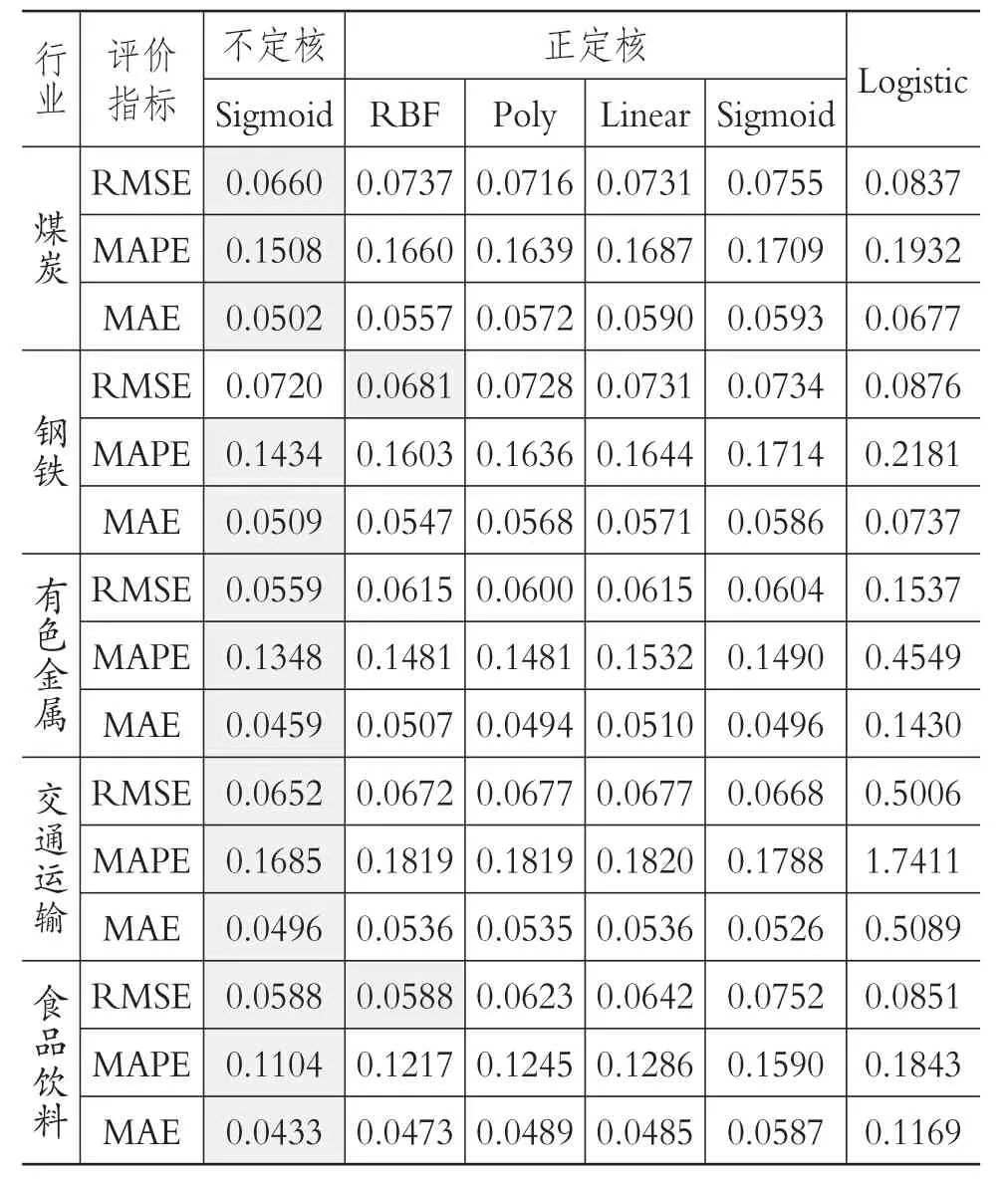
表4 分行業各模型的預測性能對比

實證研究結果表明：從模型的預測精度上看，不定核LS-SVM模型無論在整體行業還是在分行業中均展現出了優越的預測性能，表明不定核具有優異的泛化性能以及良好的可操作性。

基于上述實證結果，本文認為使用不定核LSSVM模型能夠對公司的違約概率進行良好的預測，為公司管理層的經營操作、風險防范以及監管部門調控全局、化解風險提供了優異的操作工具，并為金融監管構建了理論支持的“防火墻”。

[1] 陳藝云．中國公司債違約風險度量的理論與實證研究［J］．系統工程，2016（1）：26～33．

[2] Iturriaga F.J.L.，Sanz I.P.．Bankruptcy visualization and prediction using neural networks：A study of U.S.commercial banks［J］．Expert Sys?tems with Application，2015（6）：2857～2869．

[3] Sohn S.Y.，Kim D.H.，Yoon J.H.．Technology credit scoring model with fuzzy logistic regression［J］．Applied Soft Computing，2016（43）：150～158．

[4] Zhang Y.，Shi B.．Non-tradable shares pricing and optimal default point based on hybrid KMV models：Evidence from China［ J］．Knowledge-Based Systems，2016（110）：202 ～ 209．

[5] Yang Y.，Gu J.，Zhou Z.F.．Credit risk evaluation based on social media［J］．Environmental Research，2016（148）：582～585．

[6] 曹麟．監管資本與經濟資本存在本質區別嗎？［J］．上海金融，2014（2）：63～68．

[7] 林宇，黃迅，淳偉德，黃登仕．基于ODR-ADASYN-SVM的極端金融風險預警研究［J］．管理科學學報，2016（5）：87～101．

[8] Pan Y.，Xiao Z.，Wang X.N.，Yang D.L.．A multiple support vector machine approach to stock index forecasting with mixed frequency sampling［J］．Knowledge-Based Systems，2017（15）：90 ～ 102．

[9] Yu L.，Chen H.H.，Wang S.Y.，Lai K.K.．Evolving least squares support vector machines for stock market trend mining［J］．IEEE Transactions on Evolutionary Computation，2009（1）：87～102．

[10] 魏瑾瑞．對支持向量機混合核函數方法的再評估［J］．統計研究，2015（2）：90～96．

[11] 蘇治，盧曼，李德軒．深度學習的金融實證應用：動態、貢獻與展望［J］．金融研究，2017（5）：111～126．

[12] Xu H.M.，Xue H.，Chen X.H.，Wang Y.Y.．Solving indefinite kernel support vector machine with difference of convex functions programming［C］.Proceedings of AAAI Conference on Artifi?cial Intelligence，2017：2782～2788．

[13] Ong C.S.，Mary X.，Canu S.，Smola A.J.．Learning with non-positive kernels［C］.Proceed?ingsofInternationalConference on Machine Learning，2004：639～646．

[14] Zhu B.Z.，Han D.，Wang P.，Wu Z.C.，Zhang T.，Wei Y M.．Forecasting carbon price using empirical mode decomposition and evolution?ary least squares support vector regression［J］．Applied Energy，2017（1）：521～530．

[15] Huang X.L.，Maier A.，Hornegger J.，Suykens J.A.K.．Indefinite kernels in least squares support vector machines and principal component analysis［J］．Applied and Computational Harmonic Analy?sis，2017（1）：162 ～ 172．

[16] 曹勇，李孟剛，李剛，洪雅惠．基于信用利差與Logistic回歸的公司違約概率測算模型與實證研究［J］．運籌與管理，2016（6）：209～223．

[17] Lin H.T.，Lin C.J.．A study on sigmoid kernels for SVM and the training of non-PSD Kernels by SMO-type methods［J］．Neural Computing，2003（1）：1～32．

[18] 鐘燦輝，陳武．銀行信貸實務與管理［M］．成都：西南財經大學出版社，2015：25～35．

[19] 陳詩一．德國公司違約概率預測及其對我國信用風險管理的啟示［J］．金融研究，2008（8）：53～71．

[20] 遲國泰，潘明道，程硯秋．基于綜合判別能力的農戶小額貸款信用評價模型［J］．管理評論，2015（6）：42～57．

[21] Kwofile C.，Owusu-Ansah C.，Boadi C.．Predicting the probability of loan-default：An applica?tion of binary logistic regression［J］．Research Jour?nal of Mathematics and Statistic，2015（4）：46～52．

[22] 申敏，吳和成．國民經濟行業信用風險相依結構分析［J］．軟科學，2016（3）：126～129．

[23] 劉再杰，李艷．我國債券市場信用違約的特征、風險與應對措施［J］．新金融，2016（10）：49～53．