大型飛機機身垂直入水沖擊特性數值研究
張 旭 劉沛清 屈秋林 /
(北京航空航天大學,北京100191)
[基金項目]本文受國家自然科學基金(11502012、11772033)支持。
0 引言
大型飛機水上迫降性能的研究[1-4]離不開對物體入水過程的研究。在飛機入水的過程中,會有很大的沖擊載荷和沖擊壓強出現在結構上,同時后機身出現很大的吸力導致飛機出現大幅度的抬頭。后機身的吸力主要是由于飛機水平方向的運動引起的,而沖擊載荷和沖擊壓強主要是由于飛機的下降速度導致的。
影響物體入水沖擊過程的因素有很多,譬如物體的幾何形狀、姿態和沖擊速度等。大部分研究主要集中于軸對稱或二維物體進入平靜水面的過程。首先研究物體入水沖擊問題的是Von Krmn[5],他在研究水上飛機的入水性能時使用動量守恒和附加質量法求解了二維楔形體入水的垂向載荷。隨后,Wagner[6]考慮了水面抬升并通過擴張平板假設得出了更好的結果。Cointe、Armand[7]、Oliver[8]和Korobkin[9]等使用了匹配漸進展開法求解二維圓柱入水過程的載荷。Zhao等[10]使用邊界元方法求解了二維楔形體和艏外飄截面入水過程中的水面形狀、垂向載荷和壓強分布。Mei等[11]采用了一種解析方法求解二維楔形體、二維圓柱和艏外飄截面入水過程中的載荷。Greenhow[12]、Sun和Faltinsen[13]采用邊界元方法求解二維圓柱入水過程中的載荷,而Vandamme等[14]則使用了SPH方法來求解二維圓柱入水問題。王明振等[15]采用實驗方法研究三種水陸兩棲飛機典型橫截面在不同投放高度和質量下的入水沖擊中壓強和載荷的變化。上述研究主要集中于楔形體、圓柱、艏外飄截面和飛機截面等二維物體的入水沖擊過程。
三維物體入水問題的研究主要集中于航天器返回艙入水,而對于帶中央翼盒的機身形狀入水的研究很少。Mcgehee等[16]對Mercury返回艙的1/12比例模型以姿態角范圍在-30°~30°之間的入水沖擊載荷進行了實驗和理論分析。Stubbs[17]采用Apollo返回艙的1/4比例模型實驗研究了不同速度和姿態角的著水沖擊載荷。Wang等[18]使用LS-DYNA研究了Apollo返回艙以不同姿態角入水過程中的加速度變化,結果發現Von Kármán方法低估了初始的沖擊加速度而Wagner方法則出現了高估。以上的研究表明姿態角、速度和物體形狀都會對入水過程產生影響,同時三維物體的形狀復雜,將二維的結果直接應用到三維誤差較大。
本文利用數值模擬手段,對帶中央翼盒的細長體機身在不同姿態角、入水速度和機身尾翹角情況下的入水沖擊過程進行數值模擬,通過研究各參數變化的影響規律,達到揭示機理之目的。
技 術 研 究
1 物理模型
圖1為機身垂直入水的示意圖。笛卡爾坐標系原點定義在初始的平靜水面上,x方向平行于平靜水面指向機身后方,y方向鉛垂向上,z方向由右手螺旋定則確定;姿態角a是機身軸線與平靜水面的夾角;x1和x2是機身的兩個典型橫截面;機身以恒定速度V向下沖擊平靜水面,入水后機身受到的垂向力Fy,機身浸沒在平靜水面下的浮力Fb,兩者之差定義為機身受到的沖擊力Fi。
圖2展示了計算中的機身模型(參照某型飛機)。計算中采用1/10的縮比模型,計算模型的機身總長L=3.85m,后體長La=36.3%L,當量直徑為D=0.31m。尾翹角分別為β=3°,5°7°,如圖2(b)所示。圖2(c)展示了不同姿態角(α=8°,12°)下的機身橫截面形狀,其中x1=2.1m處為中央翼盒的典型截面,x2=3.3m處為機身尾部的典型截面,可以發現它們的形狀基本相似。
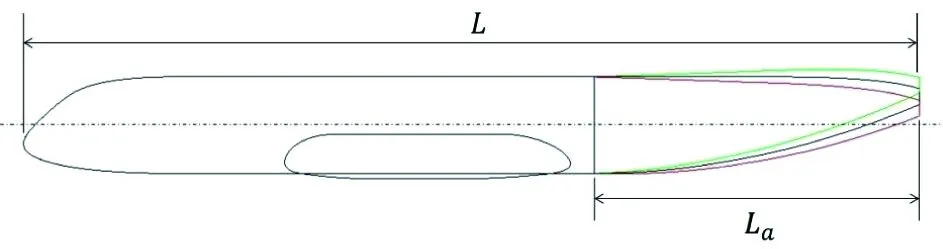
(a) 機身側視圖
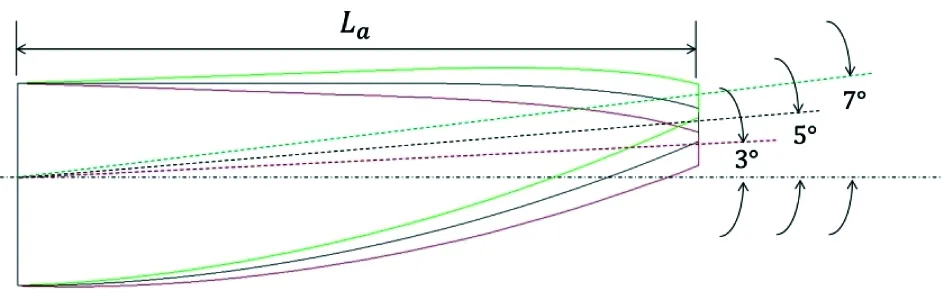
(b) 后機身
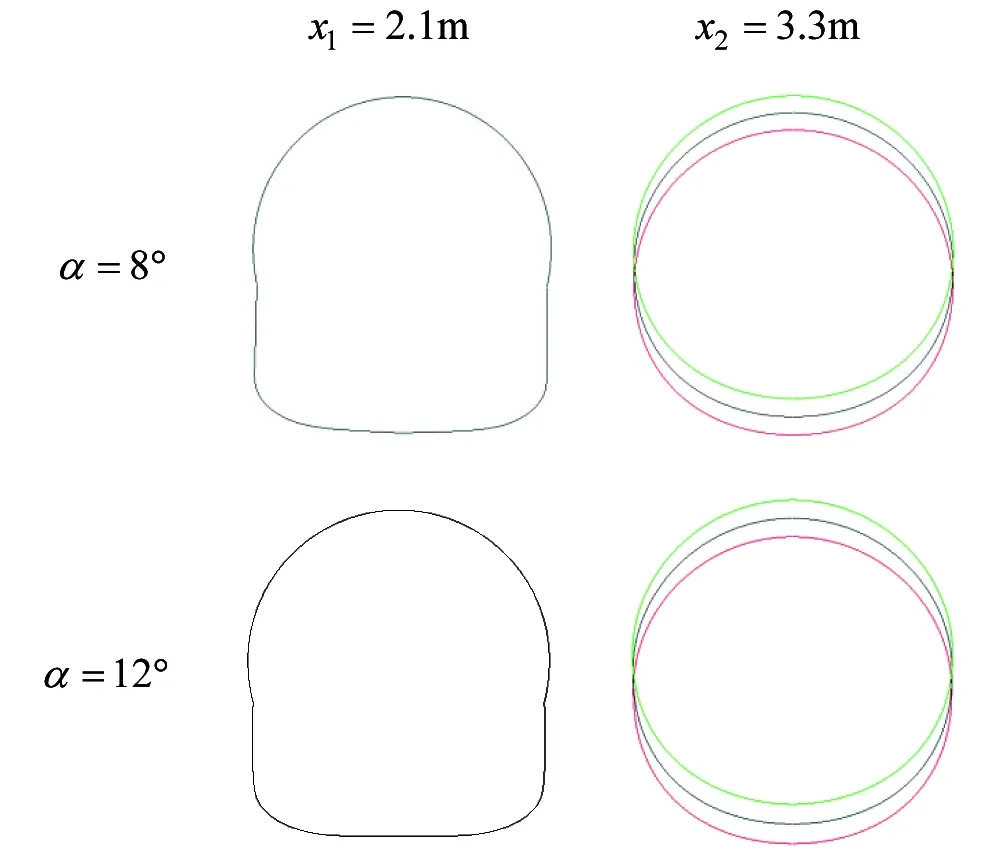
(c) 機身橫截面形狀圖2 機身模型
2 計算方法和驗證
2.1 流場求解
計算中采用ANSYS FLUENT 14.0雙精度求解器來求解非定常可壓縮的RANS方程,考慮了空氣和水的重力。湍流模擬選取可實現的k-ε模型和加強壁面函數處理。壓強速度耦合采用SIMPLE方法。對流項采用三階MUSCL格式,擴散項采用二階中心格式,非定常項采用一階隱式格式。
2.2 自由面模型
自由面的捕捉采用VOF模型,模型通過對每一個相定義體積分數來模擬該相,每一個網格單元中所有相體積分數之和等于1。對于一個網格單元,q相的體積分數定義為:γq=0意味著該單元中沒有q相;γq=1意味著該單元中充滿q相;而0<γq<1表示該單元是相間的交界面。
第q相體積分數的連續方程為:
(1)
2.3 整體動網格技術
整體動網格技術(Qu等[19])用來模擬機身和水體之間的相對運動。計算過程中,整個計算區域及其內部的網格隨著機身做剛體運動,這種方式不會出現網格的變形和重構,保證了網格的質量并節約了計算資源。
機身表面采用無滑移壁面邊界條件;計算區域的邊界為速度入口邊界條件,邊界上的體積分數設定可以保證在網格的運動中自由面保持不動。
圖3是計算區域和機身附近的網格劃分情況。計算中采用半模,計算區域大小為3L×2L×L,如圖3(a)所示,其中xy平面為對稱面。結構網格可以更好的捕捉水面,因而計算中采用了結構網格并對機身物面附近進行加密。圖3(b)展示了機身附近的網格劃分情況,最終采用的網格數量大約140萬。
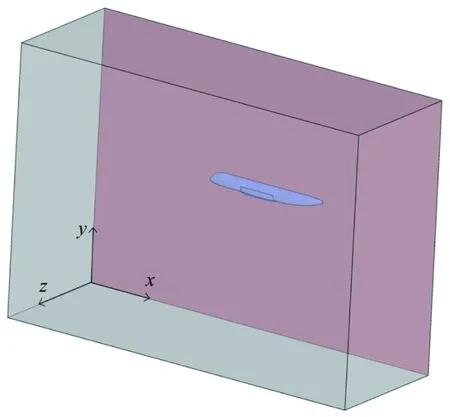
(a) 計算區域

(b) 機身附近網格圖3 計算區域和機身附近網格
2.4 網格數量和時間步長的依賴性驗證
選取尾翹角為β=5°的機身模型以α=12°姿態角,V=0.5 m/s下沉速度的入水過程,開展網格數量和時間步長的依賴性驗證。
圖4是70萬(Coarse)、140萬(Normal)和280萬(Fine)網格數量計算的垂向載荷系數時間歷程對比,其中S=π(D/2)2為典型機身界面的面積。可以看出70萬網格與140萬差距較大,而140萬與280萬差距較小,因此下文計算中選取140萬網格是合理的。
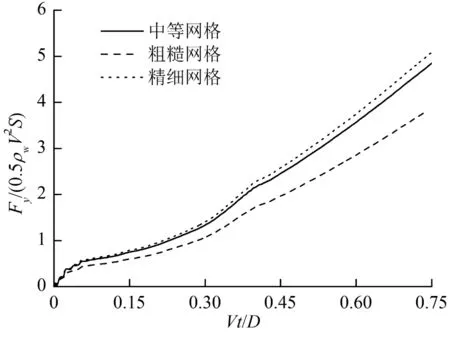
圖4 不同網格數量計算的垂向載荷系數時間歷程
圖5是Δt=10-3s、10-4s和10-5s時間步長計算的垂向載荷系數時間歷程對比,可以看出時間步長為10-3s的結果與10-4s的結果差距較大,而10-4s與10-5s的結果差距較小,因此下文計算中選取的時間步長為10-4s。
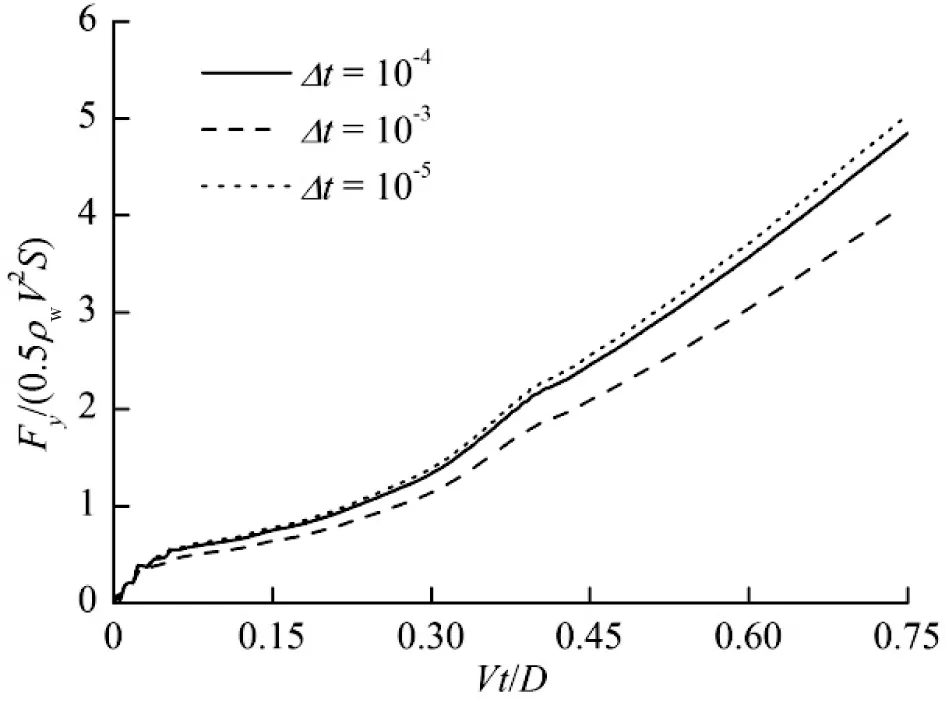
圖5 不同時間步長計算的垂向載荷系數時間歷程
2.5 計算方法驗證
本文選取Lin和Shihe[20]的圓柱入水實驗來驗證本文計算方法的精度。實驗中的壓強傳感器為Kyowa PGM-2KC(直徑5.5 mm,頻率24 KHz,量程2×105Pa),照相系統為CCD-16 MHz。圓柱材料為丙烯酸樹脂,圓柱長度20 cm,直徑20 cm,重量12.5 kg。自由降落的初始高度為0~20 cm,入水速度范圍0.76 m/s~1.98 m/s。壓強監測點相對于中心線的圓心角為0°、7.5°、15°和30°。驗證選取入水速度為0.99 m/s的實驗結果。計算中采用上述數值模擬方法對二維圓柱的入水過程進行模擬。
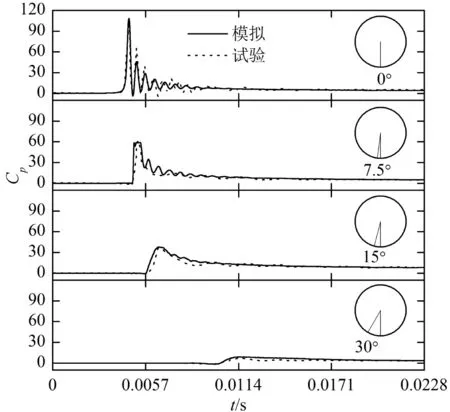
圖6 實驗和模擬的壓強系數的時間歷程對比
圖6是實驗和模擬計算的壓強系數的時間歷程對比。其中壓強系數定義為Cp=(p-p0)/(0.5ρV2),其中p為當地壓強,p0為大氣壓強,ρw為水的密度,V為觸水時刻的速度。從圖中可以看出模擬結果與實驗結果的峰值和趨勢都吻合得很好。實驗結果中7.5°和15°中壓強幾乎沒有波動而模擬中有波動,這個差異是由于實驗中三維效應導致該位置沒有空氣泡出現,而二維計算模型中出現了空氣泡。本文的數值方法可以很好地模擬入水過程。
3 計算結果與分析
為了研究入水速度、姿態角和機身尾翹角對機身垂直入水沖擊過程的影響,計算了不同尾翹角(β=3°,5°,7°)的機身以常速度進入水體的過程,其中入水速度分別為V=0.25 m/s,0.5 m/s,姿態角分別為α=8°,12°。
3.1 典型的機身入水過程
選取尾翹角為β=5°的機身模型以姿態角α=12°,V=0.5 m/s下沉速度的垂向入水過程為典型算例。圖7為該過程中的水面位置和機身腹部壓強分布。
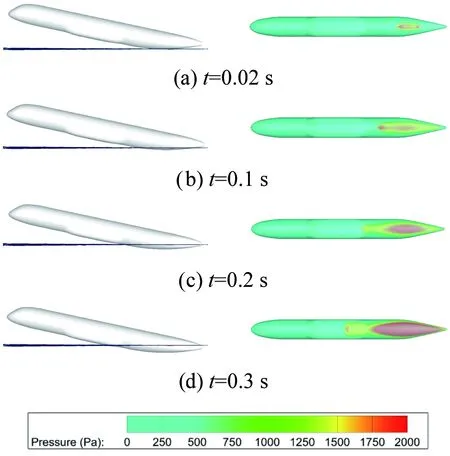
圖7 典型入水過程(β=5°,α=12°,V=0.5 m/s)中水面形狀和機身腹部壓強分布
從圖7(a)中可以看出在剛入水后不久的t=0.02 s,壓強峰值很大且出現在噴濺根部。隨著入水深度增加,壓強峰值略有減小,且與底部區域的壓強差距有所減小,如圖7(b)所示。圖7(c)為t=0.2 s時刻,此時壓強峰值已經轉移到了機身底部,而且水面已經到了中央翼盒的位置,導致局部的壓強增大。從圖7(d)可以看出,當機身浸沒深度繼續增加,壓強峰值一直在機身的底部,同時由于沖擊效應中央翼盒與水面接觸的前部位置出現了局部的壓強極大值。
在船舶研究領域,人們通常使用切片法,用純2D物體的入水沖擊特性代替3D物體截面的入水沖擊特性。為了研究這種近似帶來的誤差,本文對比典型機身截面和形狀相同的純2D物體入水沖擊特性的差別。
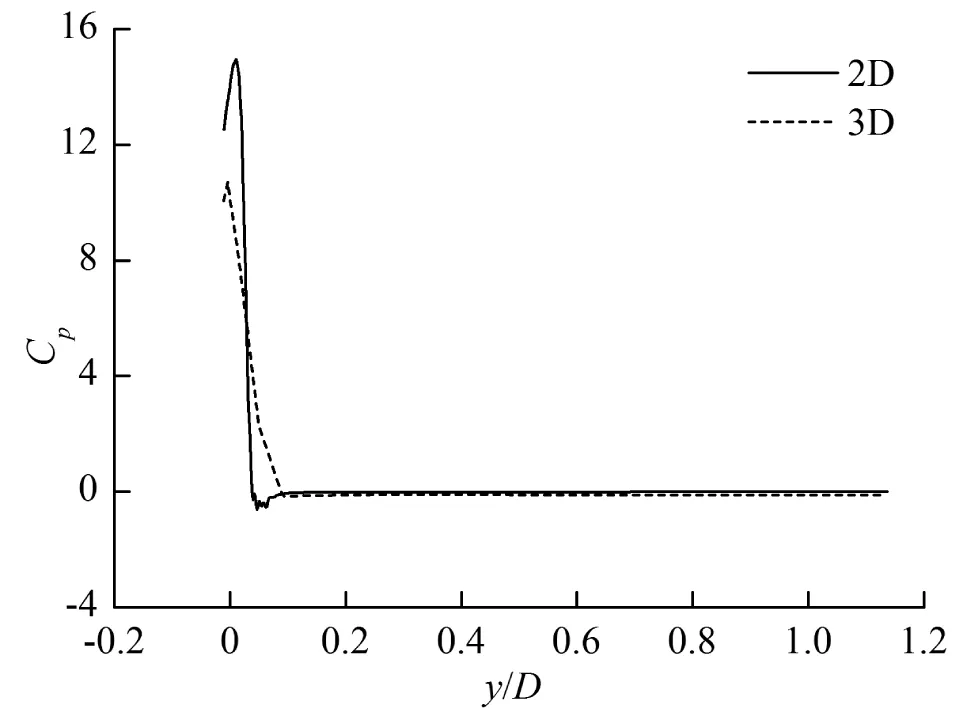
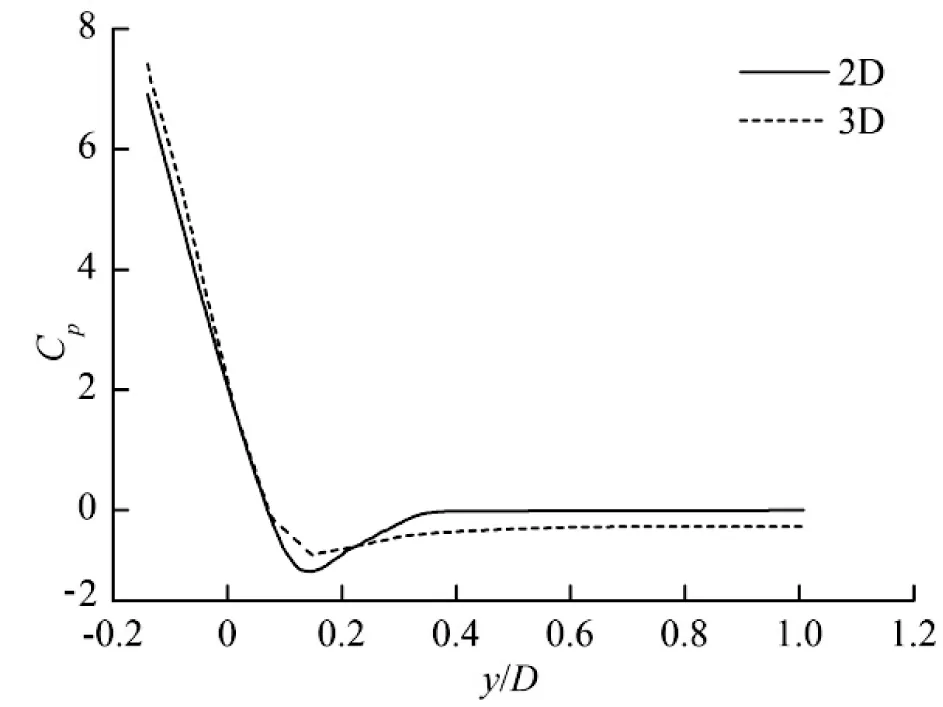
圖8是入水過程中機身x2截面和2D物體的表面壓強系數對比,其中y=0為初始時刻平靜水面的位置。可以發現3D和2D的壓強系數分布具有一定的相似性,而它們的差別主要來自3D的縱向流動和沖擊。在圖8(a)中的t=0.02 s時刻,壓強系數峰值并沒有出現在物面底部即y/D最小的地方,而是出現在水面附近的噴濺根部,由于存在縱向流動3D截面上的壓強系數峰值小于2D;隨著y/D繼續增大壓強系數迅速減小;最后y/D>0.1的部分是由于上方沒有接觸到水因而物面壓強系數基本為零。隨著入水深度的增加,在圖8(b)所示的t=0.1 s時刻,壓強系數峰值已經出現在了y/D最小的物面底部,由于縱向存在沖擊這一時刻3D的壓強系數峰值大于2D;隨著y/D的增大壓強系數迅速減小,在y/D=0.1附近出現了一些負壓,這是因為沖擊后出現了水面抬升,高于平靜水面的水受到了重力作用;隨后壓強系數上升到零附近之后保持不變(y/D>0.3)。最后圖8(c)中的t=0.3 s時刻,壓強系數峰值也是在y/D最小的底部,此時縱向沖擊影響減弱使得3D的壓強系數峰值略小于2D;隨后迅速減小直到零附近保持不變。
(a) t=0.02 s
(b) t=0.1 s
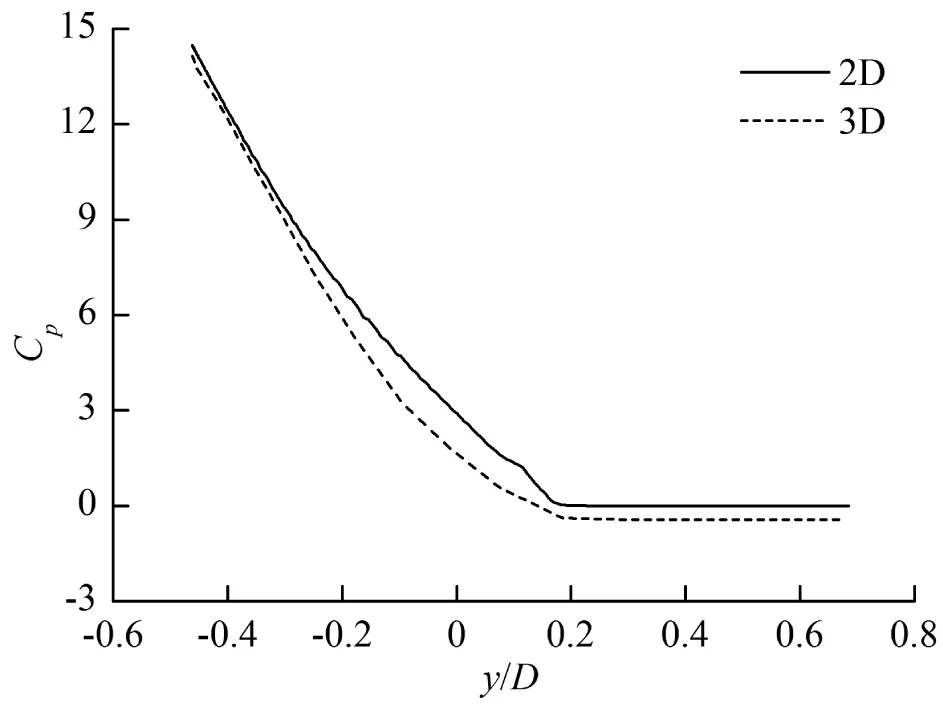
(c) t=0.3 s圖8 入水過程(β=5°,α=12°,V=0.5 m/s)中機身x2截面和2D物體表面壓強系數對比
圖9是入水過程中機身x1截面和2D物體的表面壓強系數對比。可以看出該截面上壓強系數分布的變化規律與圖8是基本一致的。在入水初期,如圖 9(a)所示,3D與2D的壓強系數峰值差別較大,這是由于此時的后機身大部分已經浸沒水面,縱向流動的影響很大使得3D的壓強系數峰值遠小于2D。
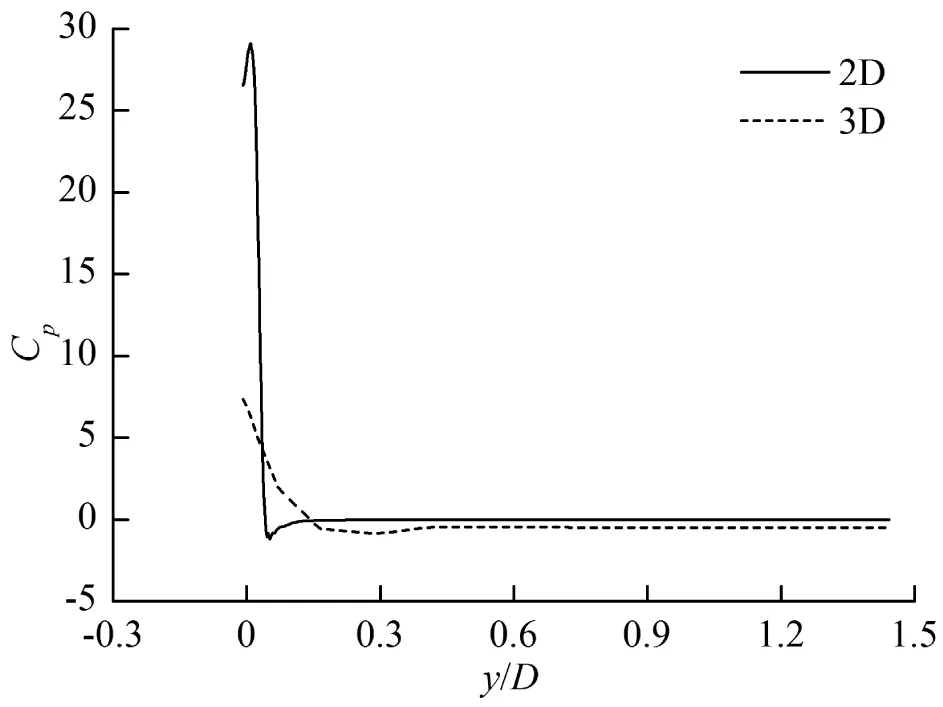
(a) t=0.34 s
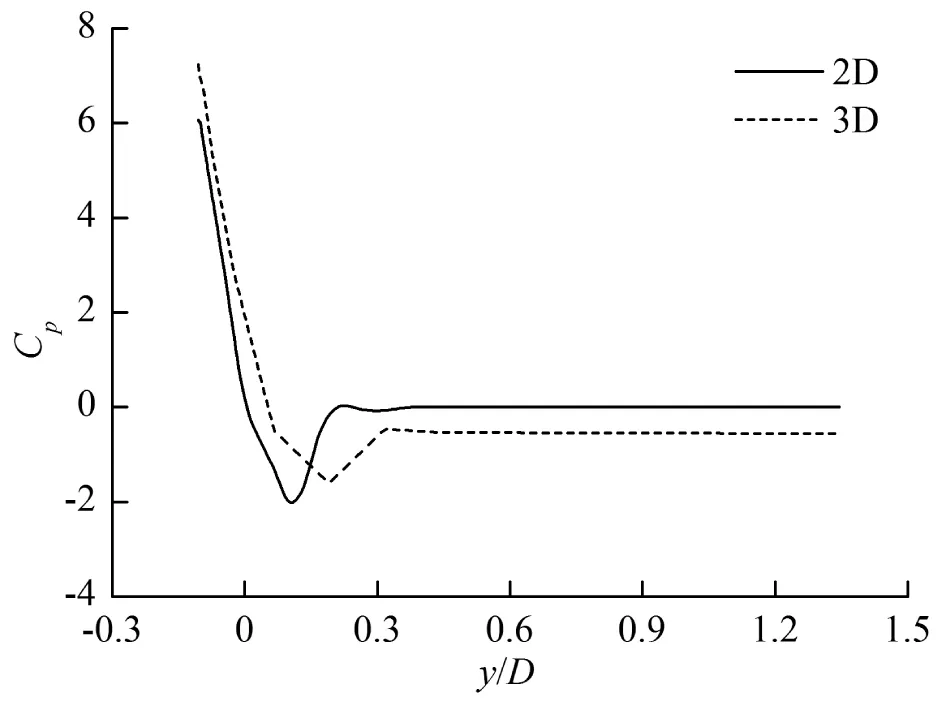
(b) t=0.4 s
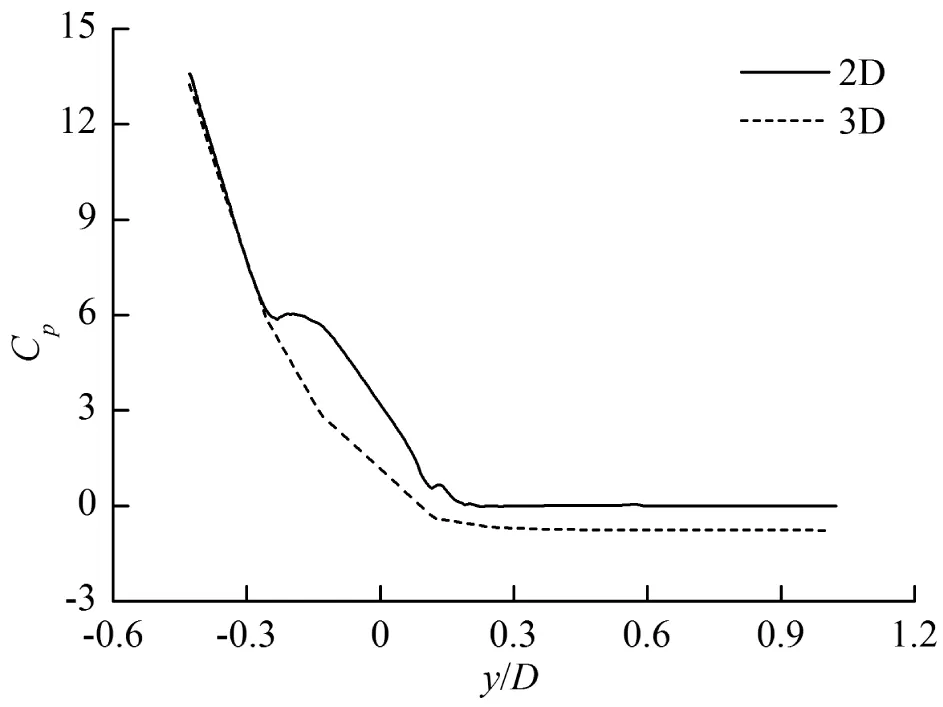
(c) t=0.6 s圖9 入水過程(β=5°,α=12°,V=0.5 m/s)中機身x1截面和2D物體表面壓強系數對比
3.2 入水速度、姿態角和尾翹角的影響
圖10是入水過程(β=5°,α=12°,V=0.5 m/s)中機身沖擊力Fi系數的時間歷程。機身剛進入水面時(Vt/D<0.07),沖擊壓強很大,同時浸潤面積迅速增加,導致沖擊力系數迅速增大;隨著入水深度的增加(0.07
可以看出,中央翼盒沖擊水面前后沖擊力系數發生了很大的變化,因而本文以中央翼盒沖擊水面的時刻為界,將機身最低點觸碰水面的時刻到中央翼盒觸碰水面的時刻稱為入水前期,之后為入水后期。
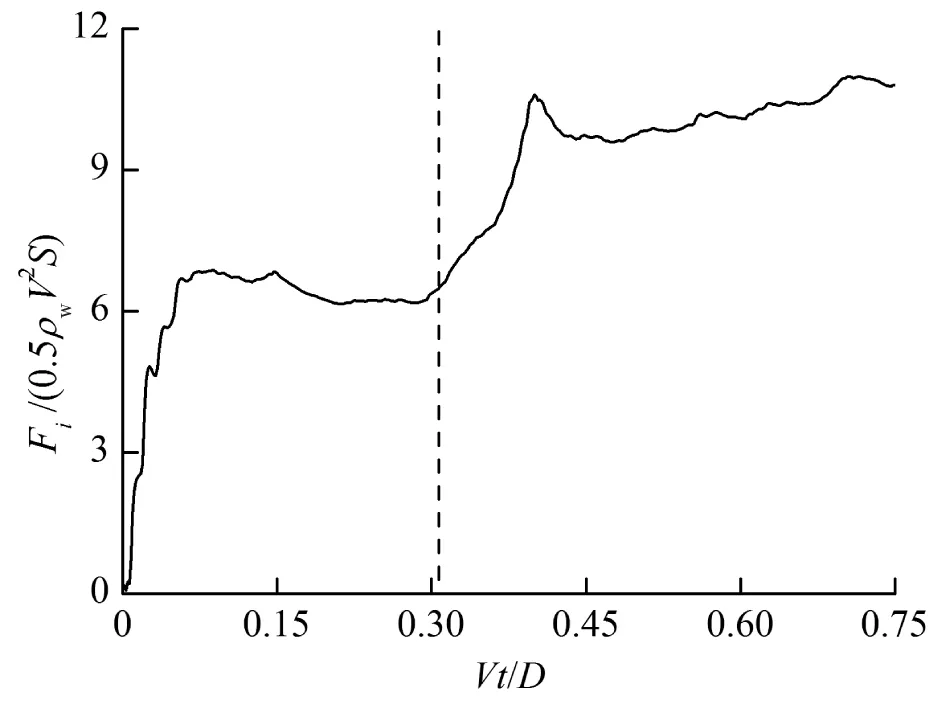
圖10 入水過程(β=5°,α=12°,V=0.5 m/s)中機身沖擊力系數時間歷程
3.2.1 入水速度
圖11為不同入水速度下(β=5°,α=12°,V=0.25 m/s,0.5 m/s)機身沖擊力系數的時間歷程對比。在同一無量時刻,入水速度較小時的浸潤面積較大,導致沖擊力系數較大。
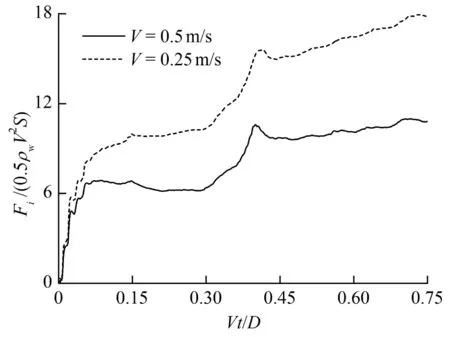
圖11 不同入水速度下(β=5°,α=12°,V=0.25 m/s,0.5 m/s)機身沖擊力系數的時間歷程
3.2.2 姿態角
圖12為不同姿態角下(β=5°,α=8°,12°,V=0.5 m/s)機身沖擊力系數的時間歷程對比。入水初期,姿態角α=8°的沖擊力系數比姿態角α=12°的略大,這是由于α=8°的浸潤面積略大;在入水后期,由于機身以α=8°入水時中央翼盒沖擊水面的時刻早于以α=12°入水的時刻,而且沖擊水面時的底部抬升角較小,這導致以α=8°入水的沖擊力系數峰值大于以α=12°入水的峰值。
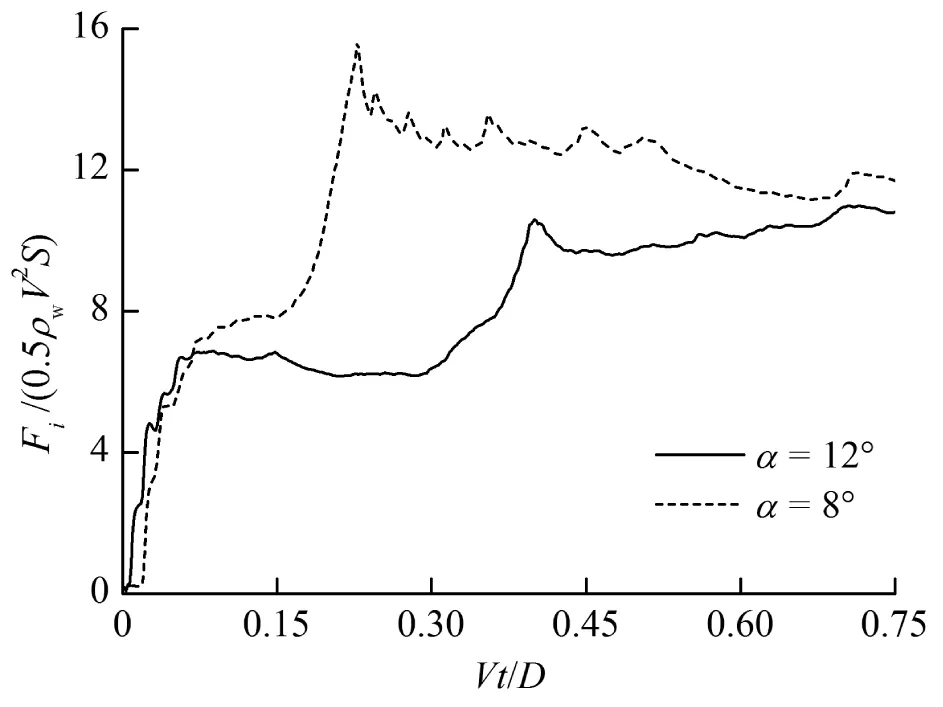
圖12 為不同姿態角下(β=5°,α=8°,12°,V=0.5 m/s)機身沖擊力系數的時間歷程
3.2.3 尾翹角
圖13為不同尾翹角下(β=3°,5°,7°,α=12°,V=0.5 m/s)機身沖擊力系數的時間歷程對比。入水初期,尾翹角大的機身浸潤面積較大,因而沖擊力系數較大;入水后期,尾翹角大的機身的中央翼盒先沖擊水面導致沖擊力先變大,但由于沖擊時的底部抬升角差別不大,因而沖擊力系數峰值差別較小。
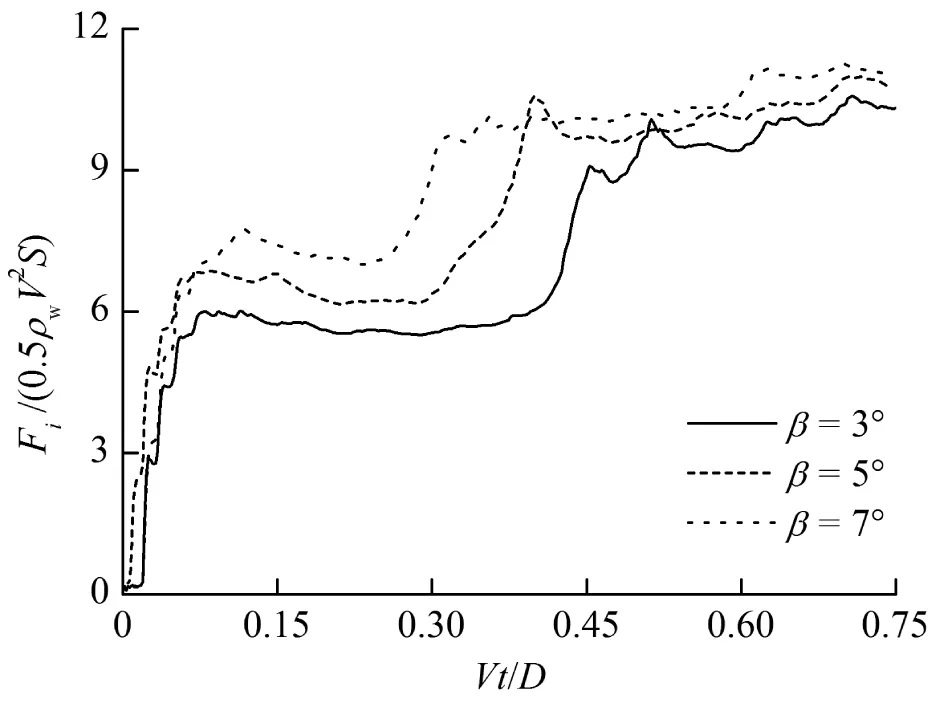
圖13 不同尾翹角下(β=3°,5°,7°,α=12°,V=0.5 m/s)機身沖擊力系數的時間歷程
4 結論
本文通過數值模擬方法研究了不同尾翹角的機身以不同速度和不同姿態角的入水過程。結果分析表明:
1) 機身入水過程中壓強峰值首先出現在噴濺根部,隨后轉移至機身底部。三維效應的影響表現為入水過程中機身截面的壓強峰值先小于二維的峰值,隨后大于二維峰值,最后又小于二維峰值。
2) 入水初期機身沖擊力系數迅速增大,而后略有回落,入水后期由于中央翼盒沖擊水面會導致沖擊力系數再次迅速增大,而后小幅震蕩。
3) 速度越大、姿態角越大、尾翹角越小,機身沖擊力系數越小。

