泳池中盤制漩渦對的形成與穩定

王盟航王志鋮李 鵬(山東省青島第二中學;山東省青島第二中學物理組，山東 青島 66000)

漩渦現象是我們生活中的一種常見現象。例如，當一艘貨輪緩慢地離開港口時，它船體的兩側就會產生許多微小的漩渦;當我們把洗手池中的塞子拔掉的時候，水體的運動也會轉化成一種漩渦運動的形式;當我們以一個適當的力度向前推一個裝有半瓶水的瓶子時，水中會形成“龍卷風”，但最終又會衰減。

最近，我們發現將盤子在游泳池中推動時(圖1)，一對漩渦可以在盤子周圍產生(圖2)。將盤子向前推一段路程后抽出，幾分鐘之后，漩渦仍然存在，并能穩定地向前運動。這對保持長期穩定狀態的漩渦引起了我們的興趣。后來，我們重復了此實驗，漩渦生成且保持穩定。為什么這樣一對漩渦能在沒有外界能量加入的情況下穩定地存在呢？

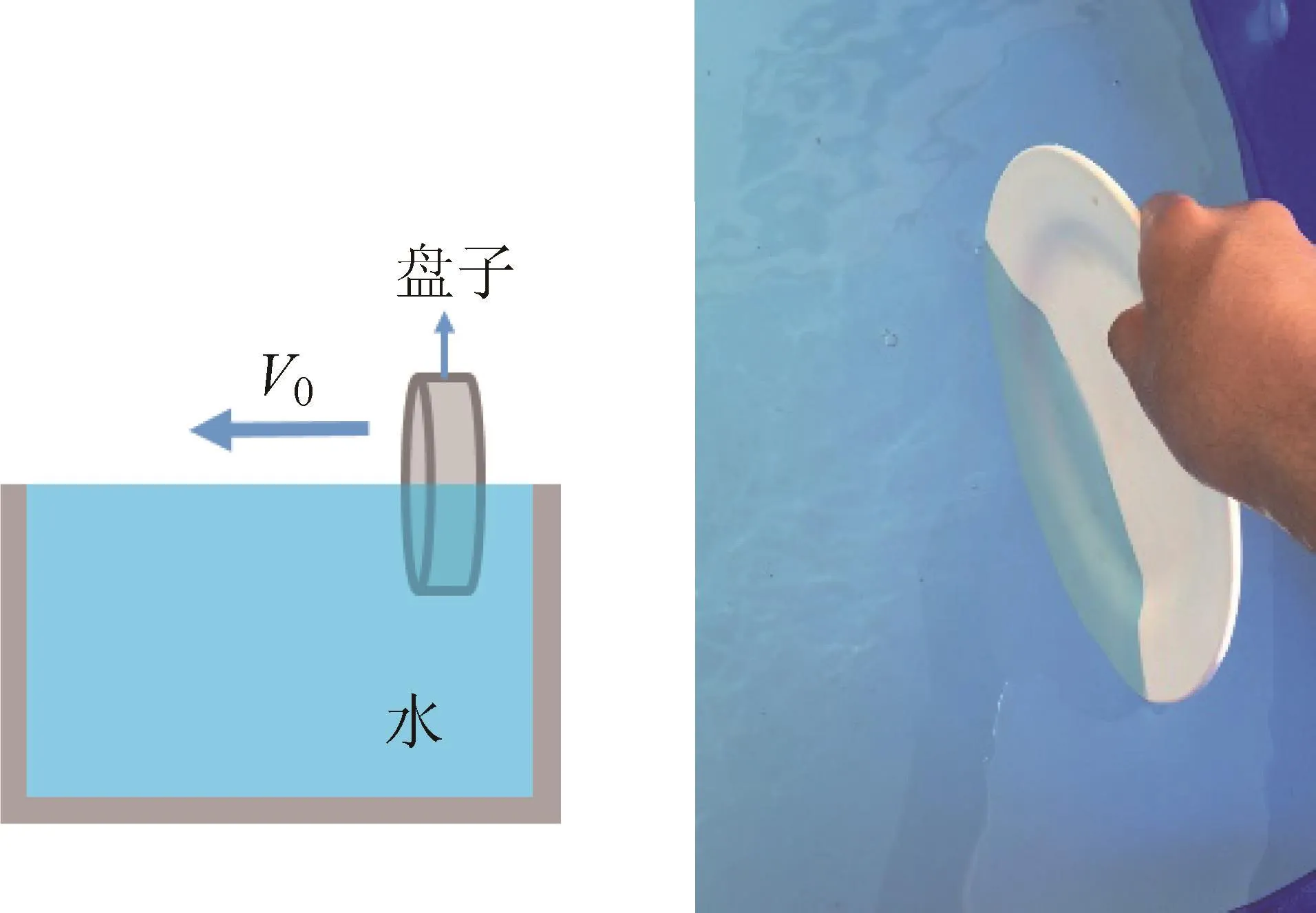
圖1　推盤子側視圖

圖2　抽出盤子后形成的一對漩渦

1　流體問題的前提假設

1.1　漩渦形成模型的流體特點

研究流體問題，首先要確定流體的模型，要從粘性和壓縮性兩點來考慮。

盤子在水中運動時，盤子物面將對流體產生阻力。因此，在盤子物面和遠離盤子的來流區域處產生速度差，導致粘性應力產生。黏性應力的作用造成了流體垂直于盤子方向的流動和漩渦的形成。同時，根據達朗貝爾佯謬[1]，當物體對流體產生阻力時需要考慮黏性。

由于推盤子的速度小于5 m/s，不會對液體壓縮做功，所以在此流體模型中，水為不可壓縮流體。

綜上，漩渦形成模型的流體特點為黏性且不可壓縮。

1.2　漩渦穩定模型的流體特點

當盤子抽出水面之后，物面產生的黏滯阻力消失，此時，黏性作用可以忽略。同時，流體未受外力做功，流體模型亦是不可壓縮流體。

綜上，漩渦向前運動時的流體特點為非黏性且不可壓縮。

1.3　變量表格

變量名稱 變量含義τ黏性應力μ沿x軸來流速度U0外部流動區域來流速度δ邊界層的厚度v沿y軸來流速度ρ流體密度ν液體動力黏滯系數l特征長度(盤子的弦長)p液體壓強g重力加速度常數ω渦量Γ環量L積分路徑R單個漩渦半徑U推動盤子的速度r距離矢量θ液體黏性系數u漩渦的角度

2　理論模型

2.1　漩渦形成模型

在實驗中，我們以流體為坐標系，通過讓盤子在水中移動一定距離產生漩渦。現在，我們把坐標系建立在盤子上(圖3)。假設盤子固定不動，流體向盤子方向流動。(風洞測試飛機模型運用了同樣的等效法)

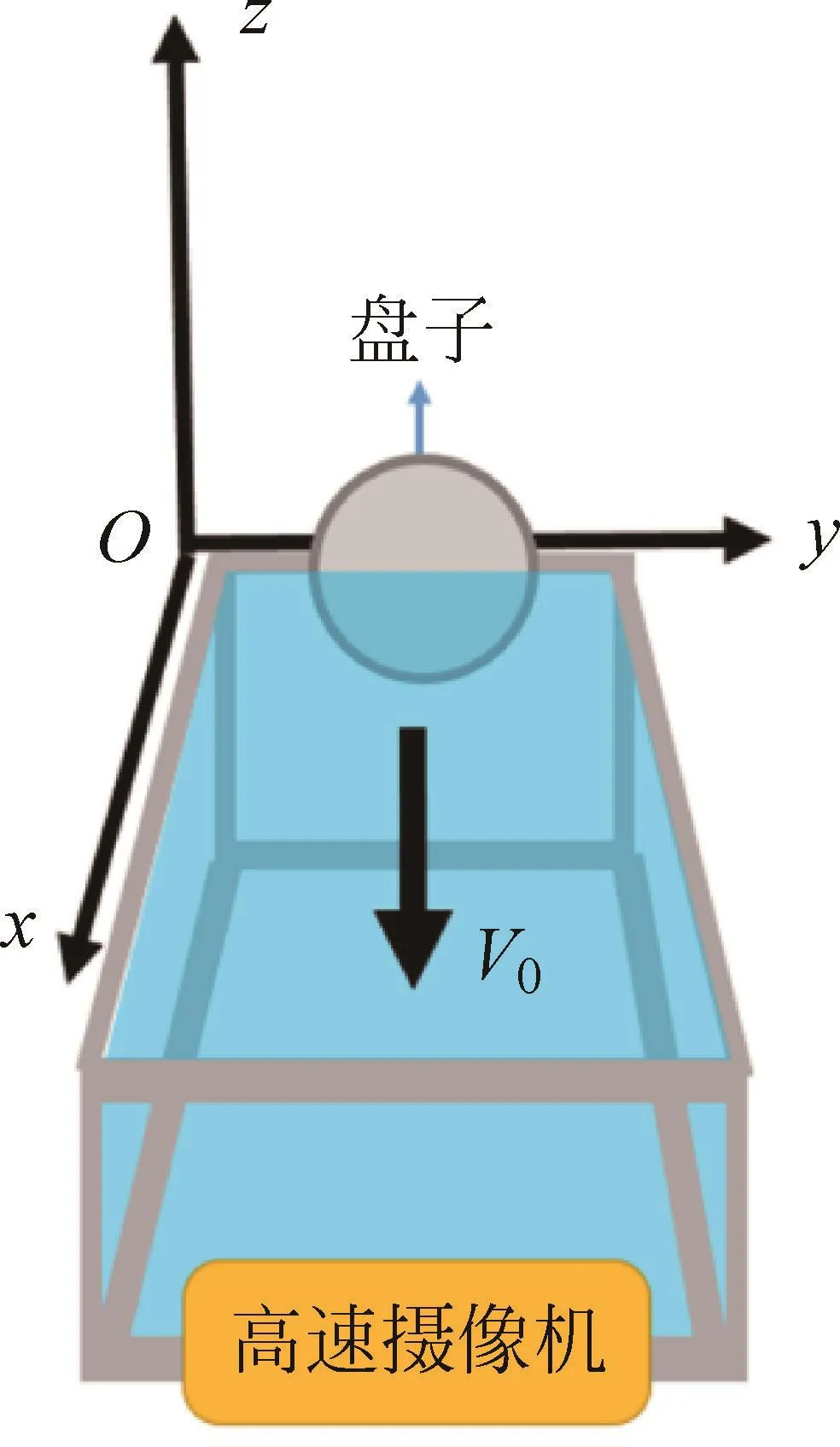
圖3　盤子坐標系示意圖

2.1.1黏性應力

當部分插入水中的盤子遇到來流速度為U0的水時，由于受到盤子物面摩擦的影響，來流速度在盤子邊緣上等于零，此時，遠離盤子物面的速度是U0。因此，在盤子邊緣和流速為U0的流體之間會產生速度梯度，進而產生黏性應力τ。

2.1.2邊界層

為了進一步探究黏性應力對流場分布的影響，我們需要引入一個邊界層的概念。邊界層是指介于來流速度為零的區域(盤子邊緣)和來流速度為U0的區域之間的區域。邊界層同時是緊貼物面且非常薄的一層區域(圖4)。

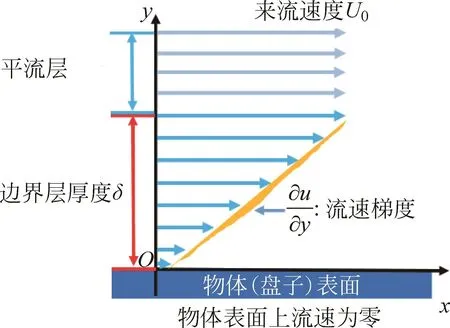
圖4　邊界層示意圖

在遠離盤子的平流區域，黏性力遠小于慣性力，可以忽略黏性。但由于邊界層內存在很大的速度梯度，黏性應力的作用效果明顯，黏性力和慣性力作用同等重要。因此，漩渦將會在狹小的邊界層內部產生，邊界層內部的情況是我們研究的重點。

納維 斯托克斯方程是用來描述黏性流體的，但是，邊界層厚度δ比特征長度l(指盤子插入水中后，盤子表面與水面相切的弦長)小得多，我們可以簡化納維 斯托克斯方程，并將其推導為普朗特邊界方程。

根據之前的分析，我們可以得到邊界層方程的基本假設為

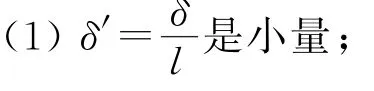
(2)黏性力和慣性力同階。

我們通過估階的方法將方程簡化[2]。

納維 斯托克斯方程

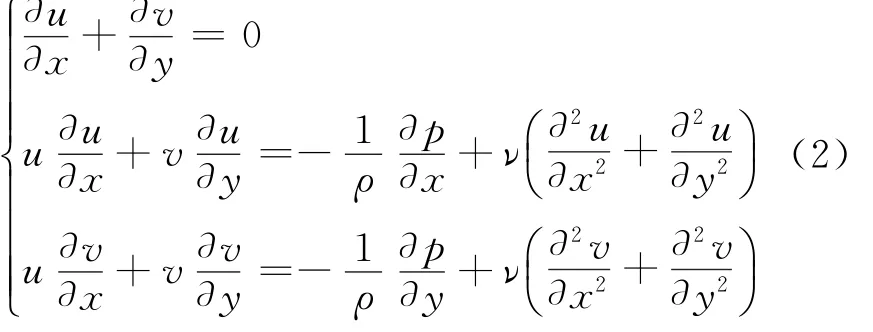
普朗特邊界方程

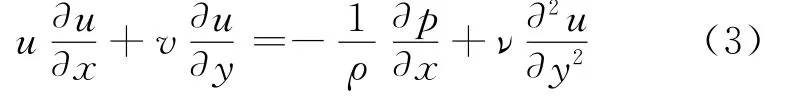
2.1.3邊界層分離

現在，我們用邊界層分離來解釋漩渦對的產生。在盤子的物面上，黏附條件為

u=0， v=0

聯立方程(4)和盤子物面黏附條件，可以推出：

聯立方程(4)和黏度系數與動力黏度系數換算公式

可以推出方程

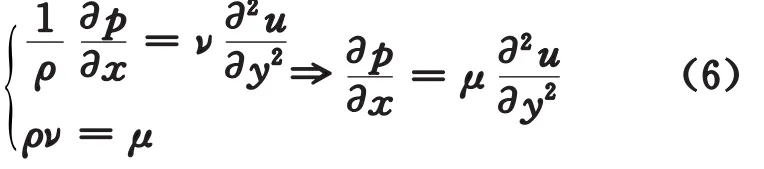
在方程(6)中，得到了壓力導數和速度曲線曲率的關系，這將便于下一步分析物面周邊流體速度場的變化。

我們先簡化盤子模型為圓柱模型來分析邊界層的分離過程。在圓柱上建立坐標系，利用LBM(Lattice Boltz mann Method)在Matlab中模擬邊界層在圓柱物面的脫離過程。圖5中展示的是圓柱周邊流體的速度場，Re=100。

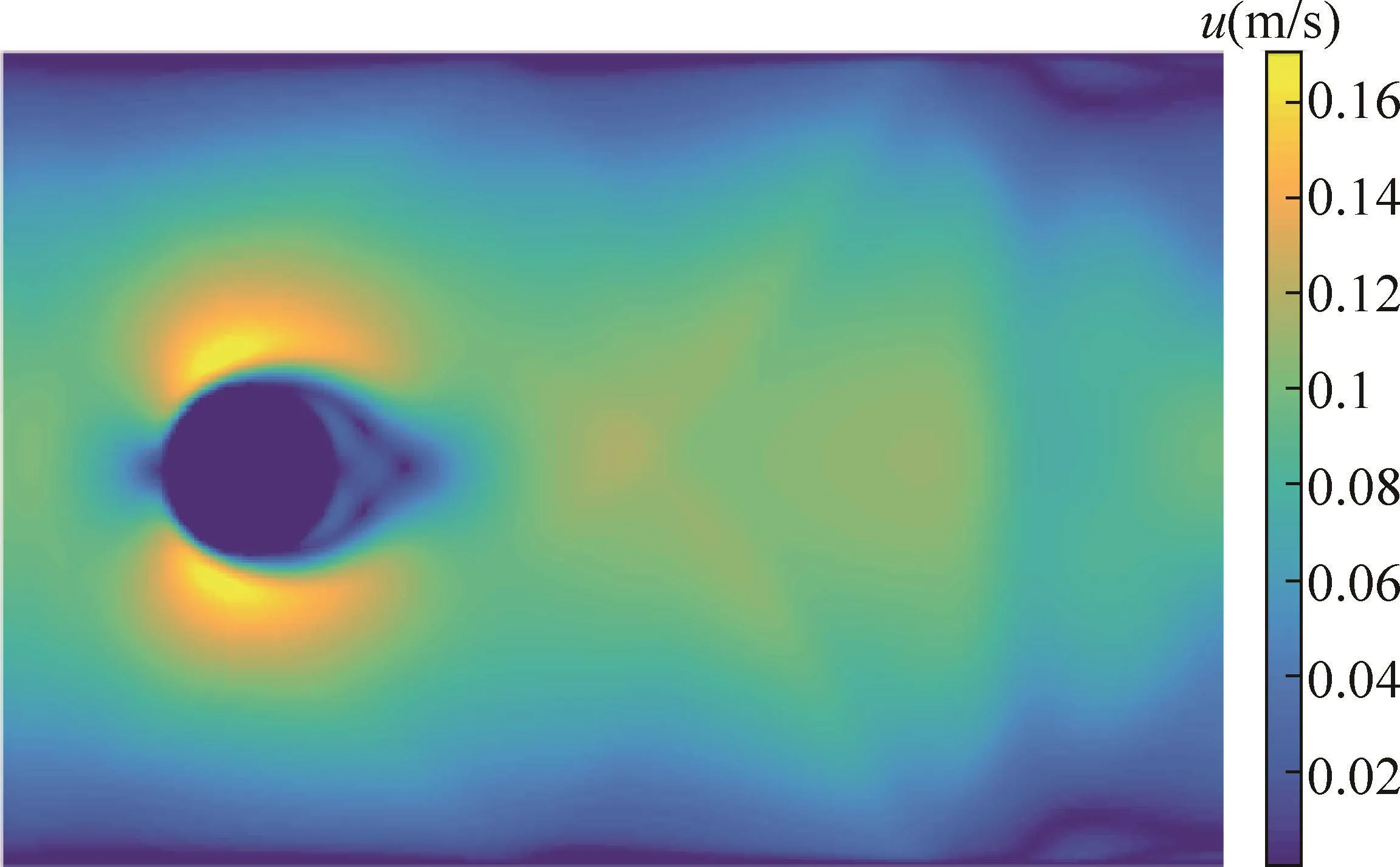
圖5　Matlab圓柱物面邊界層分離模擬

根據伯努利方程，可以通過模擬得到的速度場來推導圓柱周邊壓強場。

在圖6中，深黑色箭頭實線為添加的輔助線，用來表示來流方向。A、B、C、D 4個點代表圓柱周邊特定位置的流體。

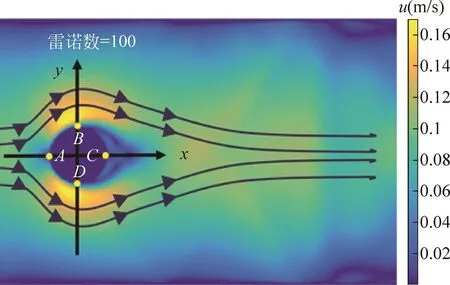
圖6　圓柱物面邊界層分離注釋

A點位于圓柱前段，流速趨近于零;B點位于圓柱一側，存在流速。此時，A點壓強將大于B點壓強，從A點到B點，壓強減小，流體質點順壓強梯度流動，沿A點流向B點，且沿x軸方向的壓強的導數小于零。

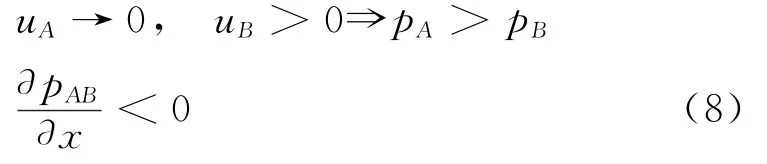
此時，根據方程(6)，可以得出邊界層內部速度曲率小于零，速度曲線沿y軸上凸，來流方向繼續保持原先方向，沒有發生回流。

圖7(a)中的淺色線條展示的是此時邊界層上的速度曲線，速度曲線在物面一側沒有發生變化，邊界層此時緊貼物面。

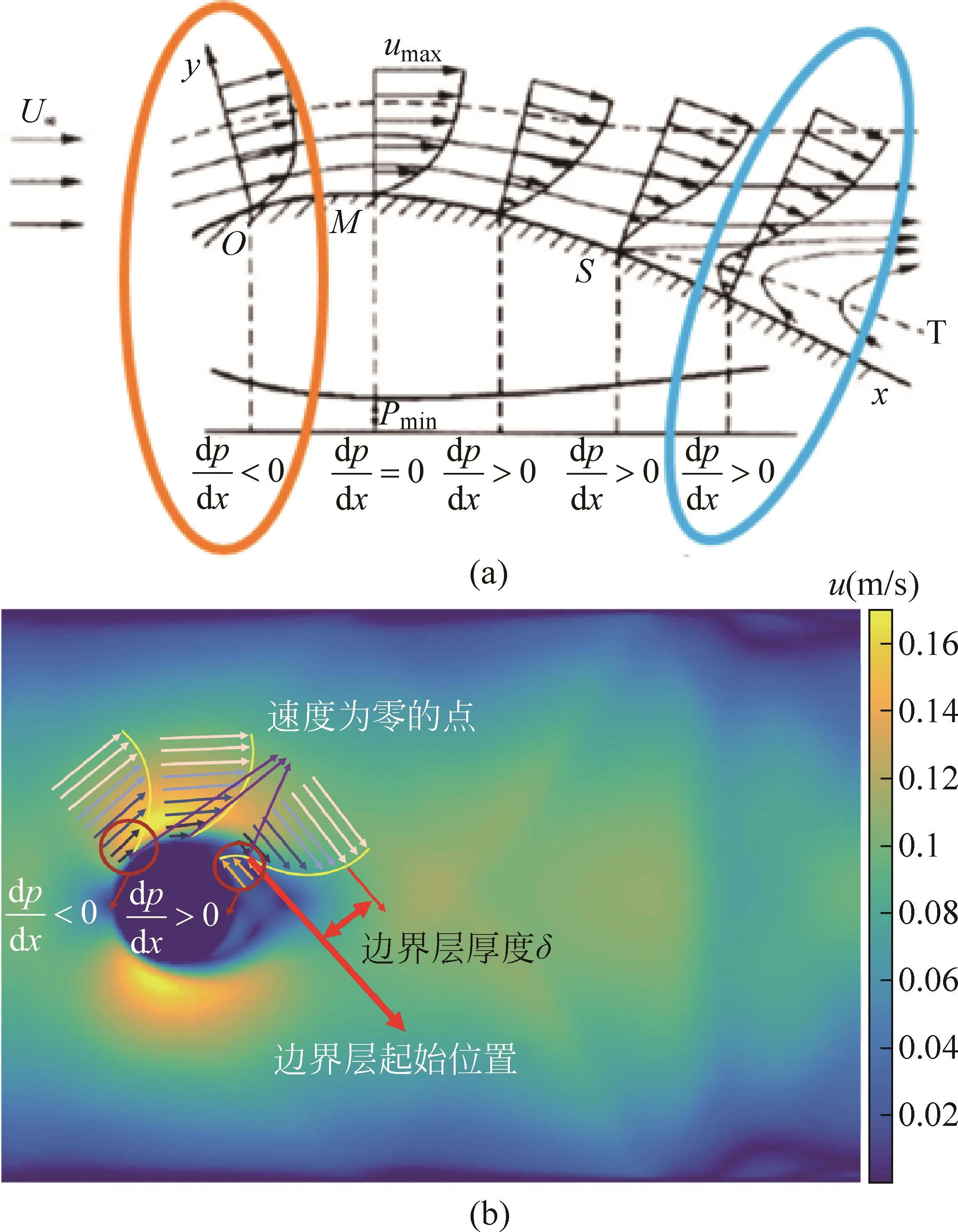
圖7　圓柱物面邊界層內速度曲線變化

回到圖6中，C點位于圓柱背側，流速趨于零，小于B點的流速。此時，從B點到C點，壓強增大，流體質點逆壓強梯度流動，因此沿著x軸的壓強梯度大于零。

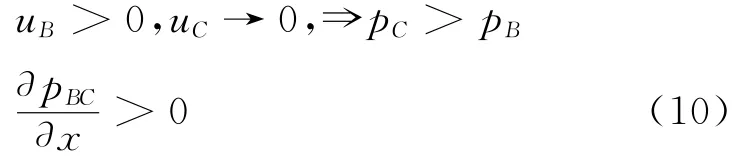
此時，根據方程(6)，可以得出在邊界層內部速度曲率大于零，臨近物面一側的速度曲線沿y軸下凸，來流方向繼續與原先方向相反，發生回流。

此時，圖7(a)中的深黑色線條表示盤子物面一側的速度曲線反曲，物面附近速度不為零，邊界層發生分離。

根據Matlab對漩渦速度場的模擬，我們發現圓柱繞流后速度分布發生了變化。速度為零的點(邊界層起點)不在圓柱體的物面上，物面附近發生回流，邊界層發生了脫離。圖7(b)中的速度曲線的標注和速度場的分布展示了漩渦成因。此時位于圓柱兩側，一對漩渦將會在流體經過圓柱繞流后出現。

2.1.4盤子模型的修正

先前我們采用圓柱模型簡化了盤子模型，因為盤子本身形狀的特殊性，現在需要對模型進行修正。

同樣，在盤子上建立坐標系。此時A點到B點在x軸方向的投影遠小于圓柱上從A點到B點的投影，可以推出盤子模型沿著x軸的壓強變化率將遠大于圓柱模型。B點到C點的壓強梯度同理可得。

因此，盤子模型產生的速度曲率變化相比圓柱模型會更加明顯，使得流速為U0的流體在接觸到盤子邊緣的同時就發生邊界層分離現象，使得漩渦對隨后產生(圖8)。

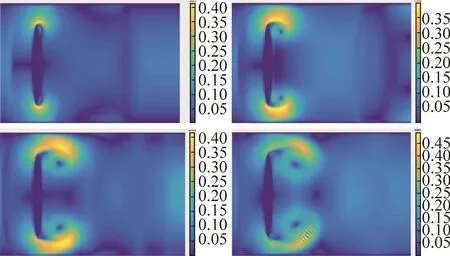
圖8　Matlab盤子邊緣邊界層分離模擬

通過改進Matlab的代碼，我們用盤子模型對邊界層分離現象進行模擬，證實了接觸盤子邊緣的同時就會發生邊界層分離，且產生更明顯的漩渦對。

2.1.5回流區域驗證

使用Fl uent編程設置盤子與平穩來流，模擬了盤子周圍的流場分布。圖9中箭頭表示每一流體質點的速度矢量。Fl uent模擬證實了在緊貼物面的區域，速度矢量發生變化，物面附近流體速度不為零且與來流速度U0方向相反，形成漩渦結構。

2.2　漩渦U形渦管穩定模型

2.2.1U形結構的形成

之前我們只對漩渦進行了二維的研究，現在需要進一步探究這對漩渦在流體中的三維結構。

由于部分盤子是浸在水中，運動的流體與盤子物面接觸時，在盤子的半圓形邊緣上均會發生邊界層分離，并產生湍流和漩渦現象。因此，漩渦會沿著盤子浸入水中的邊緣形成(如圖10所示)。

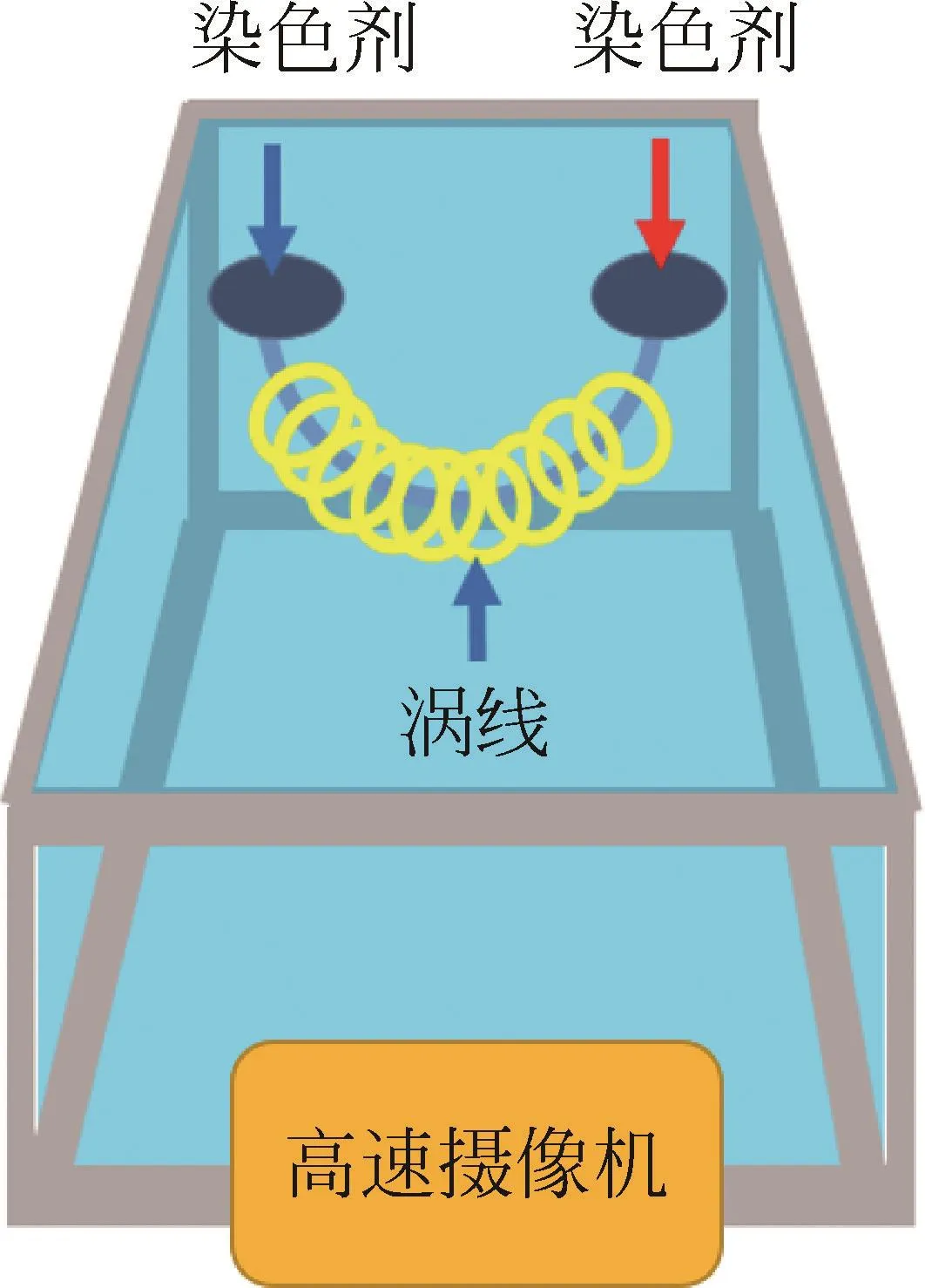
圖10　漩渦U形結構示意圖

這些連續在盤子邊緣的漩渦將最終形成U形的聯通結構。利用染色劑對其進行染色(如圖11所示)，發現染料能沿著U形結構從一個漩渦中心，向另外一個漩渦中心輸送，反之亦然;同時，染料跟隨漩渦的U形結構一同向前運動。

圖11　漩渦U形結構實際染色圖

染色實驗說明了U形結構的性質不是一種波，而是具有傳遞物質性質的結構。與此同時，我們曾試圖故意破壞漩渦的U形結構。例如，在水池中央樹立一根粗桿(直徑3c m)，當漩渦對從粗桿中央經過時，U形結構會因為粗桿物面產生的阻力而斷裂，這一對漩渦發生能量耗散，并逐漸解旋并消失。

這個特殊的U形結構可能是保持漩渦穩定的重要條件，通過查閱相關資料，推斷此結構可能為漩渦的渦管。

因此，接下來將要驗證漩渦U形結構是否為渦管，同時建立漩渦漩渦U形渦管穩定模型。

2.2.2漩渦行進狀態的流體模型

當利用盤子在水池中產生漩渦后，我們通過機械臂的電磁鐵將盤子抽出，漩渦對會一同以一個幾乎恒定的速度向前運動。此時，物面從流體中消失，邊界層不再存在，慣性力遠大于黏性力，漩渦達到一種穩態，可以忽略流體的黏性作用。

在納維-斯托克斯方程中，

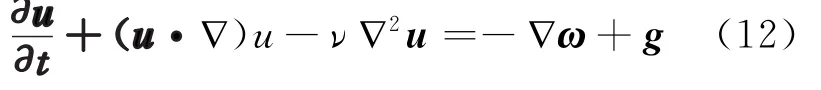
ν?2u是黏性項，ν是流體的動力黏滯系數，速度場的矢量拉普拉斯是

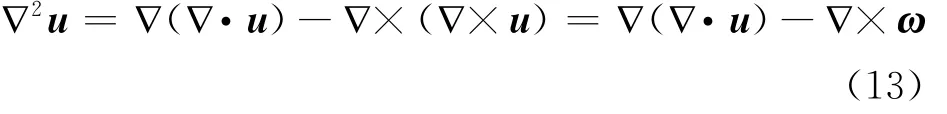
漩渦引發的速度場是螺線型的，即?·u=0，因此?(?·u)=0。另一方面，在漩渦的渦絲模型中，渦絲以外流場的渦量是零，所以?×ω=0。此時黏性項就可以從納維 斯托克斯場方程中消除掉，故我們可以把渦絲在流體中的運動看作是沒有阻力且液體無黏性。

2.2.3渦量

對于流體中的漩渦來說，最關鍵的物理量是漩渦的渦量：ω=(ξ，η，ζ)，渦量為速度場的旋度。ω=?×u

根據亥姆霍茲第一定理[2]，漩渦渦絲上的每一點都與渦量向量平行，因此滿足方程：

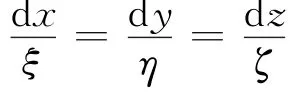
通過擴展這個定理，可以解釋染料沿渦絲傳遞并繞著渦絲中心旋轉的原因;此推論也證實了渦絲是在流體中跟隨漩渦一同向前運動，而不是向前或向外擴散。

漩渦通常由多條渦絲圍成的一個閉合的曲面構成渦管(如圖12所示)，若渦管存在渦量，同時渦量處處相等，即形成穩定的渦管結構，那么這個漩渦將是穩定的。

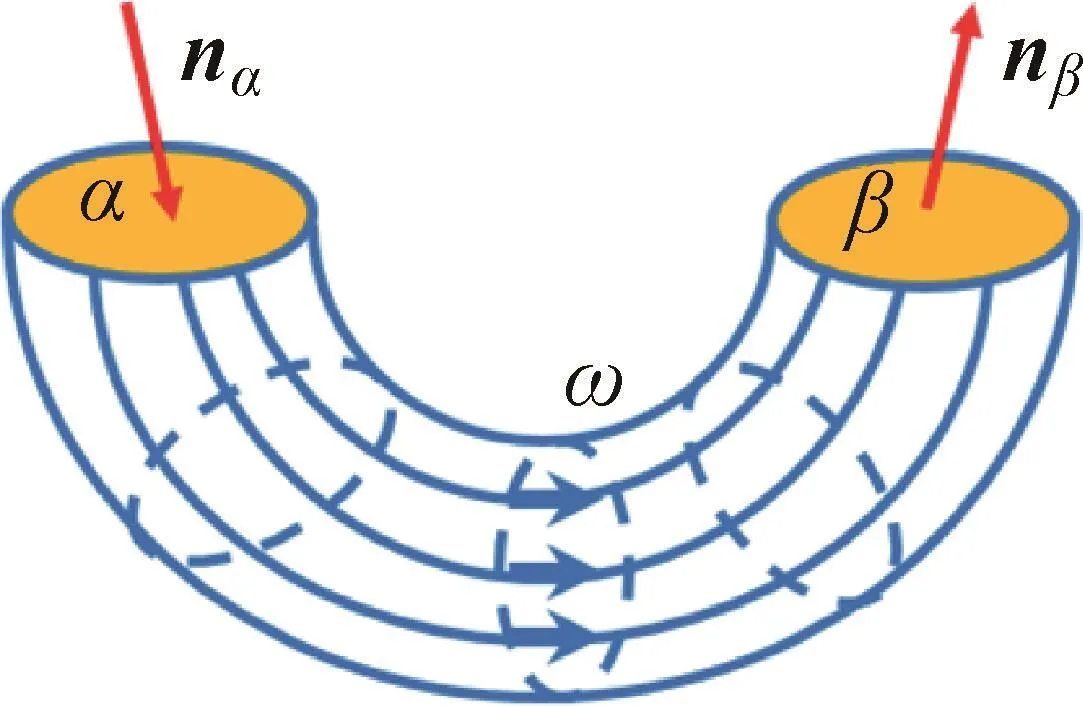
圖12　渦管示意圖

2.2.4U形渦管穩定模型

速度環量Γ是指沿著一個閉合曲線c速度的線積分;根據斯托克斯定理，速度環量和渦量之間還有如下關系

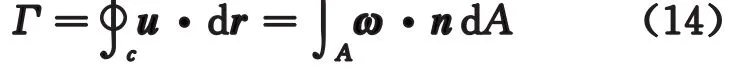
這里的速度環量表示為漩渦的渦管強度。我們將這對漩渦的三維結構取出(即為圖12)并計算它的速度環量，再把原式轉化成體積積分的形式

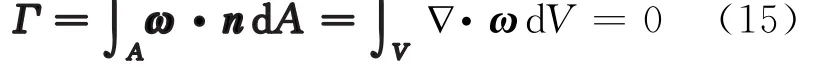
我們得到對渦管體積積分的結果是零。

再將漩渦的渦管強度利用渦管的3個表面(α面、β面和側面)的速度環量的和來表示

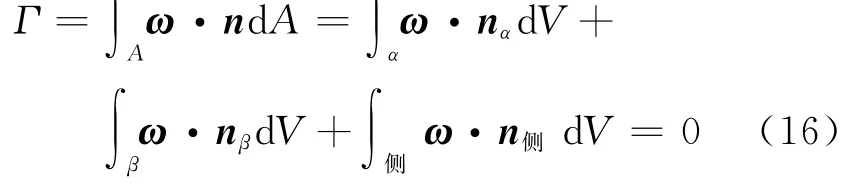
因為側面速度環量為零，可以得到

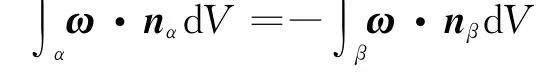
根據α面、β面的法向量的關系為

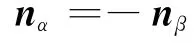
可以得到：再漩渦渦管的橫截面上，渦量處處相等。

同時，無黏性流體的渦旋管強度不隨時間的改變而改變，所以渦量在漩渦運動過程中保持恒定。

這類渦管模型完全符合泳池中漩渦對的運動狀態和自身特點。

將渦量處處相等進一步推廣可得：一個渦旋的渦管不能以一端無限小的形式存在，否則它的渦量將無限大，所以渦管必須向兩端延伸至水面的邊界(泳池中的漩渦對)或者形成閉合的環(空氣中的煙圈)。

根據我們用盤子制出的一對漩渦的形態來看，它形成的渦管結構是向兩端延伸至水面的結構(圖12)，因此，這類渦管結構是這對漩渦能夠穩定存在的原因。

2.3　漩渦存在特點

通過進行PIV實驗，我們用CCD相機記錄了漩渦在一個流體切面上的流場分布和速度場分布的情況，并探究漩渦存在時的速度場特點

漩渦的速度場和漩渦的渦量場是相互關聯的。定義上，漩渦速度的旋度即是渦量。另一方面，我們推斷漩渦的渦量場能通過畢奧 薩伐爾定律推導出漩渦的速度場。這個推斷是由分析PIV實驗得到的漩渦流場圖像和在Mathematica中對半圓形通電導線的磁場進行數值積分的結果對比得來。這對漩渦的U形渦管附近產生的速度場u的速度環量Γ(圖13(a))與半圓形電流強度為I的通電導線產生的磁感應強度B(圖13(b))非常相似。

方程(17)將速度與速度環量聯系：

安培定律將磁感應強度和電流聯系：

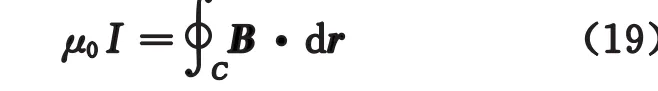
我們利用畢奧 薩伐爾定律推導漩渦速度場，即是漩渦的引發速度場：

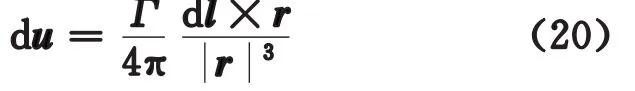
在方程(20)中，d l是渦管的一小段，Γ是渦管強度，是由漩渦形成時的初始條件決定的。下面進行積分

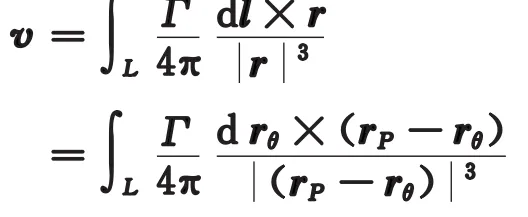
rP=(x，y，z)是流體質點P的位置，

從圖13的對比結果中，看出漩渦對的速度場和半圓形通電導線的磁場非常相似。

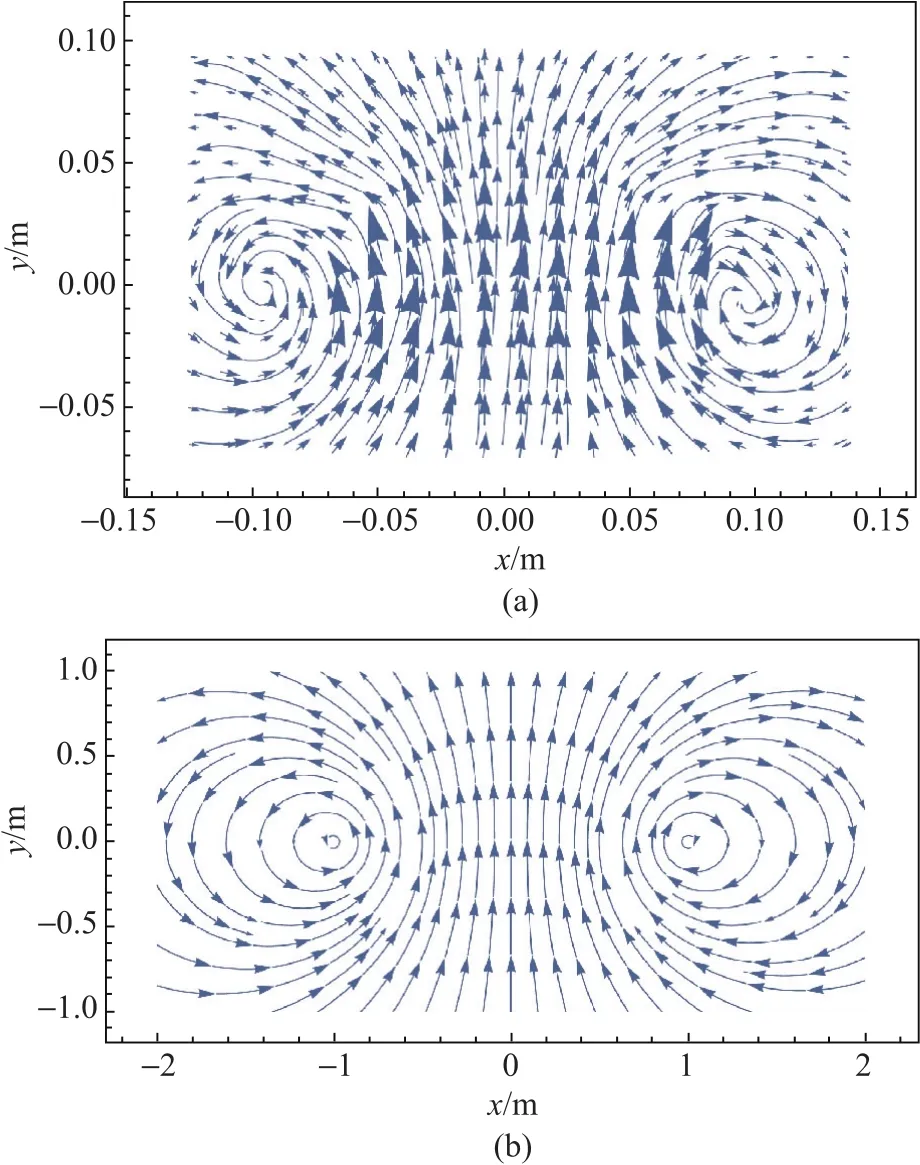
圖13　漩渦對的速度場和半圓形通電導線的磁場

3　實驗裝置

3.1　實驗設備

(1)PIV(particle image velocimetry)粒子示蹤技術。PIV設備使用CCD工業相機，PIV粒子水和3瓦綠色激光器組成。示蹤粒子浮在水中的各個層上，當有流體運動時，粒子的軌跡便可以記錄漩渦的流場、速度場。

(2)機械臂。利用步進電機、CCM直線導軌、工業自動化控制器等設備組成機械臂運動單元，步進電機結合伺服電機精確控制盤子向前移動的速度和加速度。同時利用彈簧、電磁鐵、電磁繼電器和導軌制成盤子回收裝置，以保證漩渦生成后盤子能被及時并且豎直抽出，減少人手產生的實驗誤差。

3.2　實驗方法

利用激光器產生扇形激光平面照射在PIV粒子水中，產生漩渦后，利用CCD相機(20 ms/張)記錄PIV粒子的運動情況。

圖14　實驗設備

3.3　預實驗

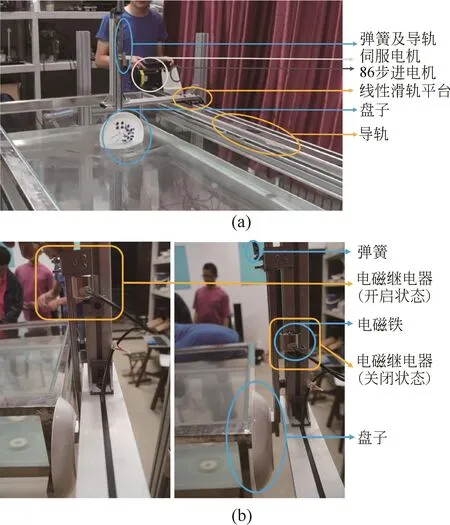
圖15　機械臂

我們進行預實驗來描繪機械臂的速度曲線，從而測試機械臂的速度控制是否精確。利用激光器產生扇形激光平面照射在PIV粒子水中，產生漩渦后，利用CCD相機(20 ms/張)記錄PIV粒子的運動情況。

4　實驗結果

4.1　漩渦的前進速度

圖16展示了漩渦向前運動時的位移 時間圖像，通過Origin進行線性擬合，我們得出漩渦向前運動的速度是一個定值，驗證了之前的假設，即漩渦在運動過程中，周圍流體對于漩渦來說是無粘的。

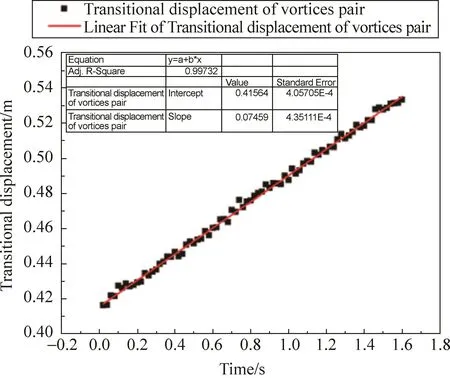
圖16 漩渦前進位移—時間圖

4.2　漩渦的平均動能

圖17展示了漩渦向前運動時平均動能的變化。從中發現，漩渦動能在減少，漩渦在耗散。但是，漩渦的擴散幾乎是穩定的，漩渦的衰減是很小的。

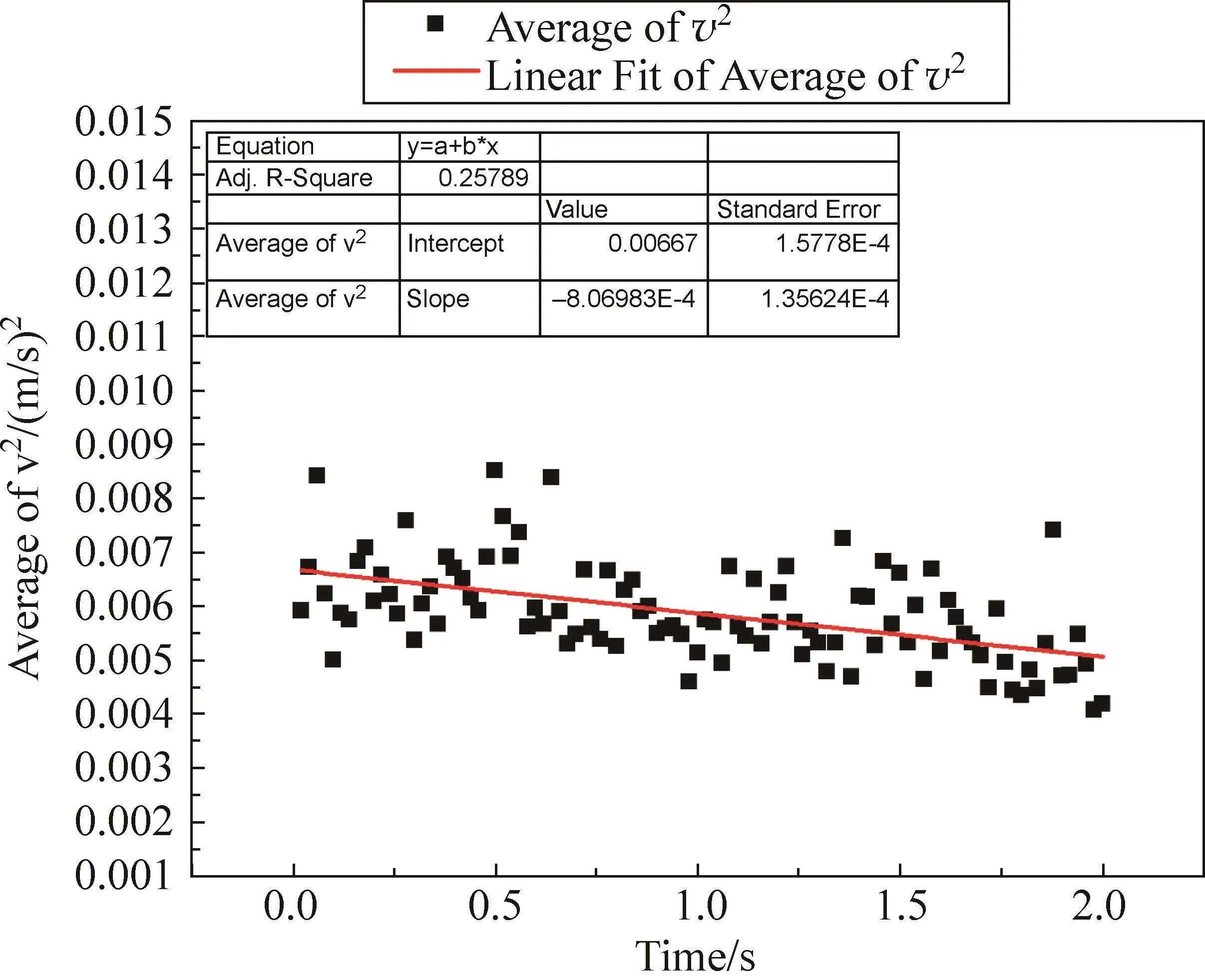
圖17 漩渦平均速度平方—時間圖

4.3　漩渦的渦量

圖18展示了漩渦向前運動時漩渦的渦量變化。漩渦渦量在減小，說明漩渦的穩定性在下降。同漩渦的平均動能一樣，渦量減少很小，所以漩渦能保持穩定很長時間。

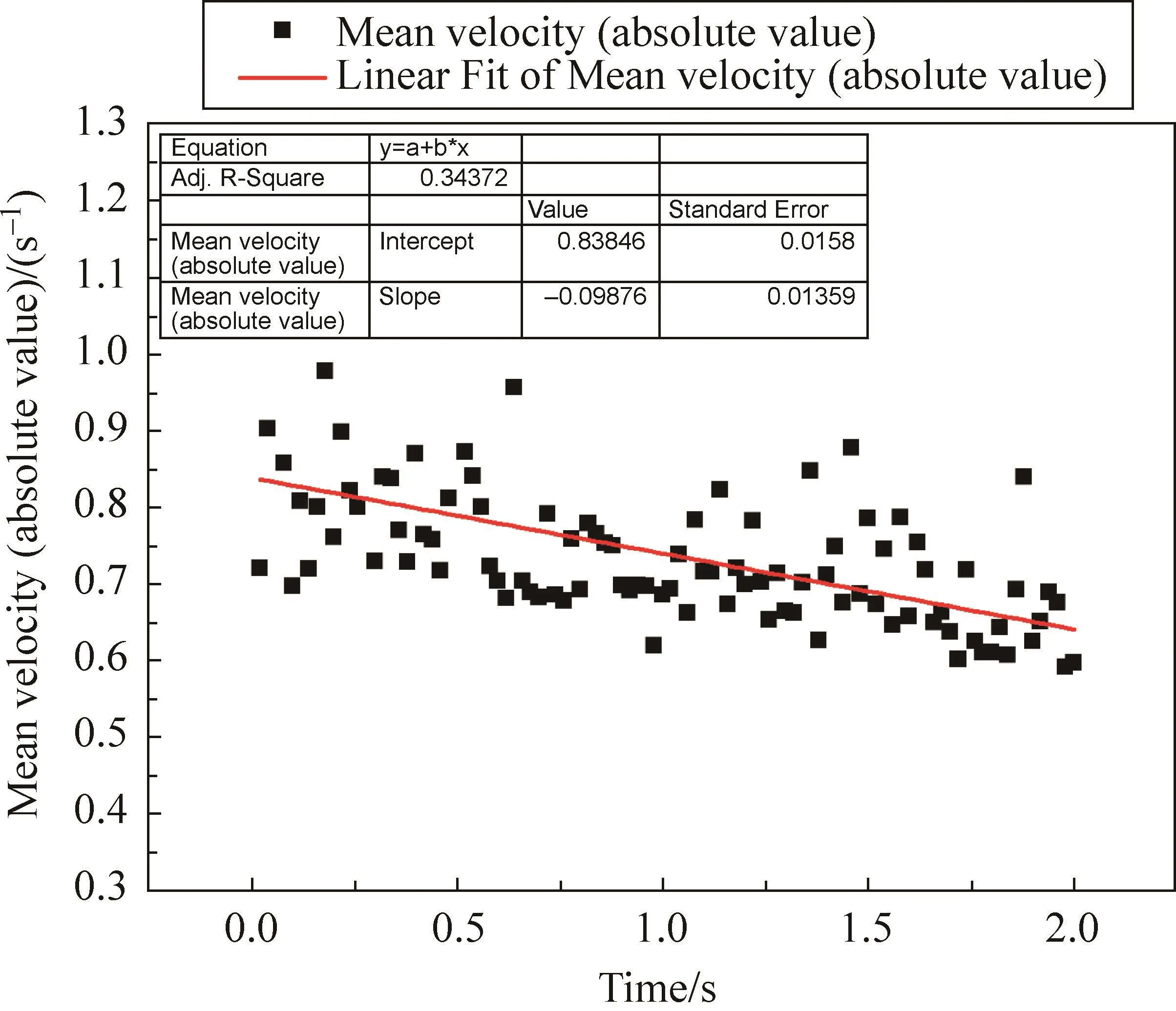
圖18　平均渦量(絕對值)—時間圖

5　總結

5.1　漩渦的形成

通過簡化納維 斯托克斯方程得到普朗特邊

界層方程，我們推導并解釋了為何在大Re數情況下，邊界層內的速度曲率發生變化，物面上的邊界層會發生分離，使得漩渦產生。通過計算機模擬軟件Matlab和Fluent，我們對模型進行了修正，并對理論中提出的回流區域進行了驗證。

5.2　漩渦的穩定模型

通過計算簡化的納維 斯托克斯方程，證明在漩渦對向前運動時，粘性作用可以被忽略。通過研究渦旋對的U形結構，并利用渦管的模型解釋了漩渦對的U形結構，證明了渦量在渦管上處處相等，同時，渦管也是漩渦對保持穩定而不迅速耗散的原因。

5.3　漩渦的存在特點

利用畢奧-薩伐爾定律的形式對漩渦對的速度場進行積分，同時利用Mathematica對半圓形通電導線的磁場進行模擬，發現漩渦的速度場和半圓形通電導線產生的磁場有極大的相似性，進一步說明了漩渦的引發速度場可以通過畢奧 薩伐爾定律推導，方便了我們分析漩渦的速度場。

5.4　漩渦的運動特點

從PIV實驗得到的實驗數據和圖像中，分析了漩渦的運動模式，發現漩渦前進速度保持恒定，且耗散很小。