鋼筋超高性能混凝土梁抗剪性能試驗研究

陳寶春, 吳前文, 黃卿維, 馬熙倫, 蘇家戰

(福州大學土木工程學院, 福建 福州　350116)

0　引言

超高性能混凝土(ultra-high performance concrete, UHPC)是一種具有超高抗壓、 抗拉強度、 高韌性和高耐久性的新型水泥基復合材料, 它包含活性粉末混凝土(RPC)、 超高性能纖維增強混凝土(UHPFRC)等[1-2].將UHPC用于梁構件中能夠提高構件的承載能力、 減小尺寸和減少鋼筋的用量.抗剪承載力是結構受力的重要內容, 文獻[3-5]對UHPC梁受剪性能進行試驗研究, 其截面型式有矩形、 T形和I形等, 試驗參數有剪跨比、 箍筋率、 縱筋率和纖維摻量等.UHPC作為一種新型材料, 其材料組份與特性有別于普通混凝土, 使得UHPC梁的受剪破壞機理也有別于普通混凝土梁.盡管國內外學者對UHPC梁的抗剪性能已開展一定的研究, 但由于UHPC抗剪機理的復雜性, 對UHPC梁的抗剪破壞形態、 極限承載力等方面還未有一致的結論.文獻[6]基于桁架-拱模型, 通過UHPC梁的抗剪機理分析, 提出考慮UHPC的抗拉作用的抗剪承載力計算公式, 計算結果與收集到UHPC梁的抗剪試驗結果吻合較好, 但該文未進行試驗研究.本研究在文獻[6]的基礎上考慮鋼纖維摻量、 剪跨比、 箍筋配箍率、 縱筋配筋率4個影響因素, 制作11根試驗梁進行UHPC梁的抗剪性能試驗研究.通過試驗研究, 進一步揭示UHPC梁的抗剪破壞機理, 并對文獻[6]提出的UHPC抗剪承載力計算公式進行進一步的論證與修正.

1　試驗概況

1.1　試驗梁

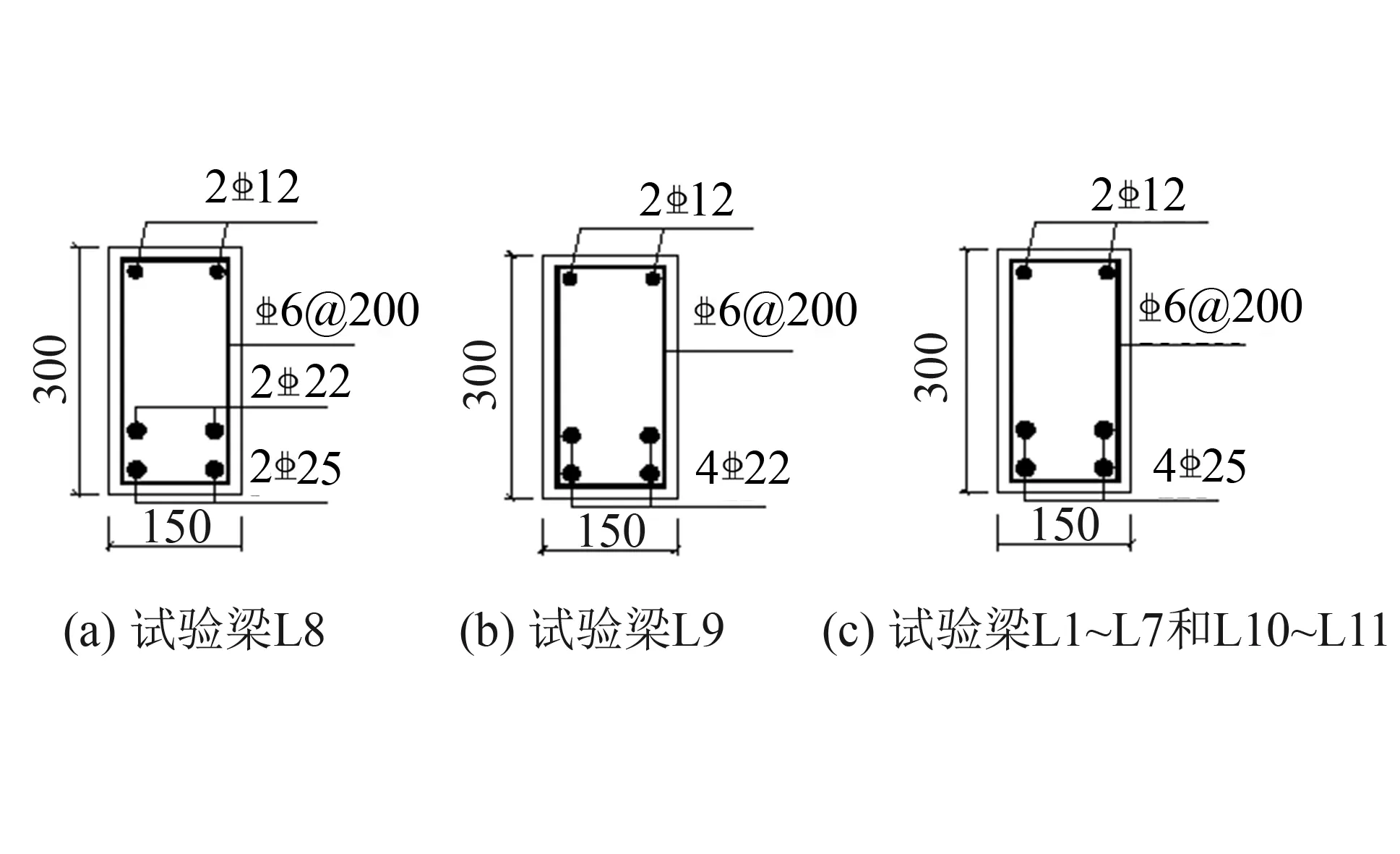
圖1　部分梁截面尺寸及配筋(單位： mm)　Fig.1　Sectional dimension and reinforcement of beams (unit: mm)

本試驗共設計了11根矩形截面梁, 各試驗梁的截面尺寸相同, 部分梁截面尺寸與配筋如圖1所示.梁長1 200 mm, 計算跨度1 000 mm.試驗梁的主要變化參數為： 鋼纖維體積摻量Vf、 剪跨比λ、 箍筋配箍率ρsv及縱筋配筋率ρs.試驗梁參數詳見表1.其中L5無箍筋, L6和L7箍筋間距分別為100 mm和150 mm, 其余梁箍筋間距均為200 mm； L8下部為2根直徑25 mm和2根直徑22 mm的鋼筋, L9下部采用4根直徑22 mm的鋼筋, L1～L7和L10～L11的下部縱筋均采用4根直徑25 mm的鋼筋.本文的荷載值為千斤頂所施加的荷載值F, 而受剪承載力V=F/2.

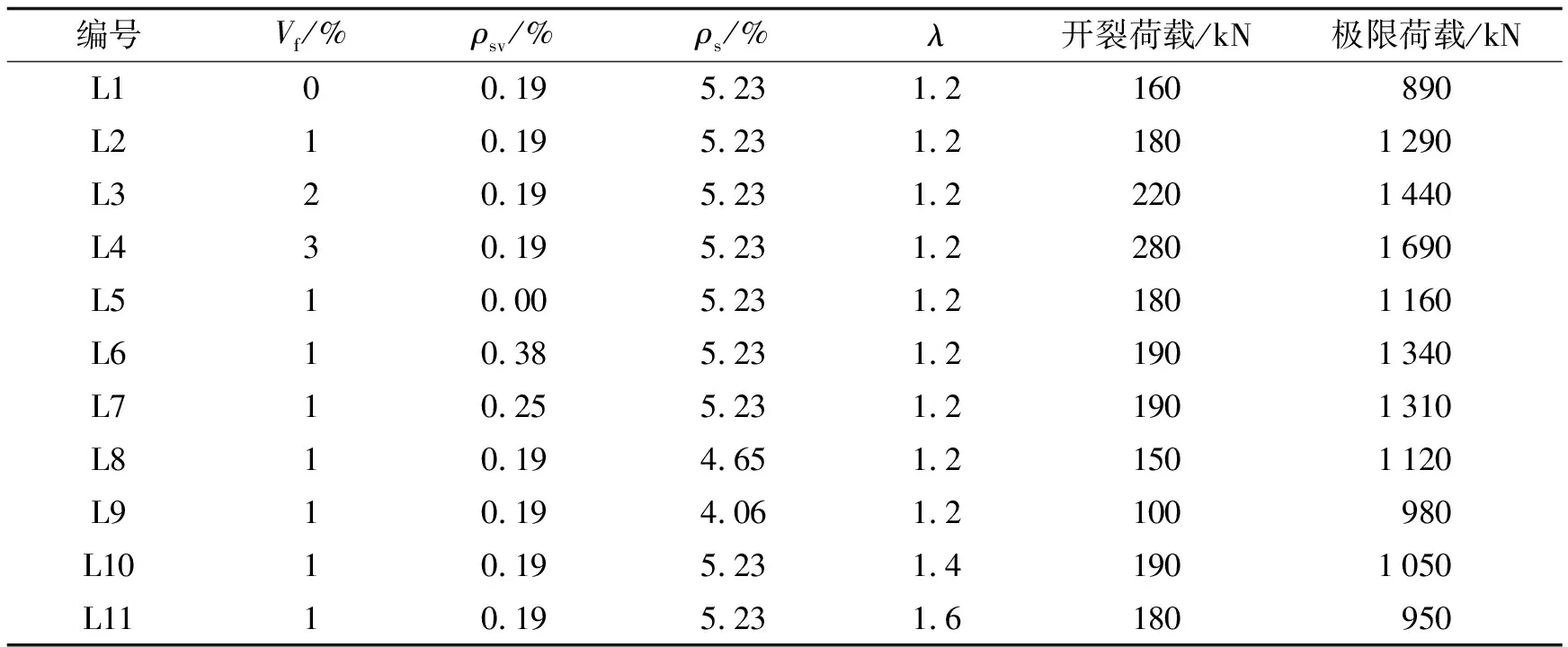
表1　試驗梁參數

1.2　試驗裝置與測量方案

試驗通過2 000 kN千斤頂與荷載分配梁系統對試驗梁進行四分點加載, 加載裝置照片如圖2所示.

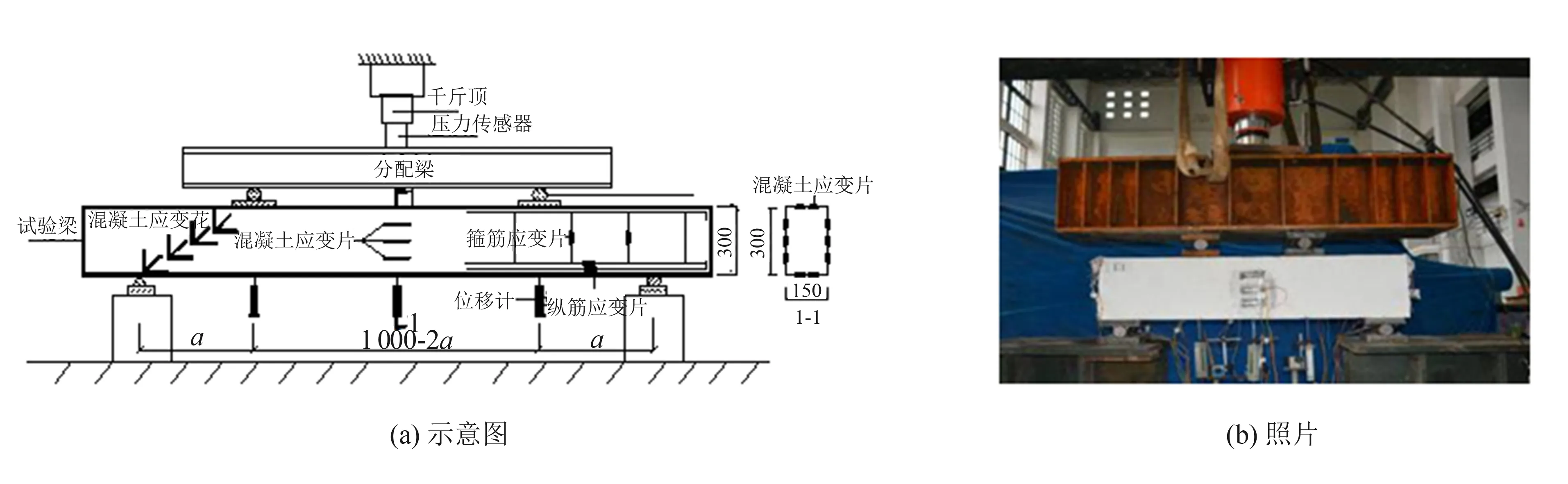
圖2　試件加載裝置與測點布置圖(單位： mm)Fig.2　Test setup and measuring point layout(unit： mm)

試驗梁在跨中和兩個加載點位置處布置3個位移測點進行撓度測試, 在剪跨區的縱筋、 箍筋和UHPC分別布置應變片進行縱向應變和剪應變的測試, 具體測試截面與測點布置見圖2.其中, 采用裂縫測寬儀進行UHPC梁裂縫寬度的測試.

1.3　材料性能

UHPC的配合比： 水膠比為0.18, 水泥∶硅灰∶細砂∶減水劑=1∶0.3∶1.2∶0.025, 鋼纖維體積率分別為0%、 1%、 2%、 3%.試塊與試驗梁同批澆筑且在同條件下進行養護.UHPC試塊尺寸采用100 mm× 100 mm×100 mm、 100 mm×100 mm×300 mm分別測得UHPC立方體抗壓強度fc與彈性模量Ec, 單軸拉伸強度ft采用有效尺寸為50 mm×100 mm×150 mm的啞鈴型試件.UHPC和鋼筋力學性能測定結果分別如表2和表3所示.

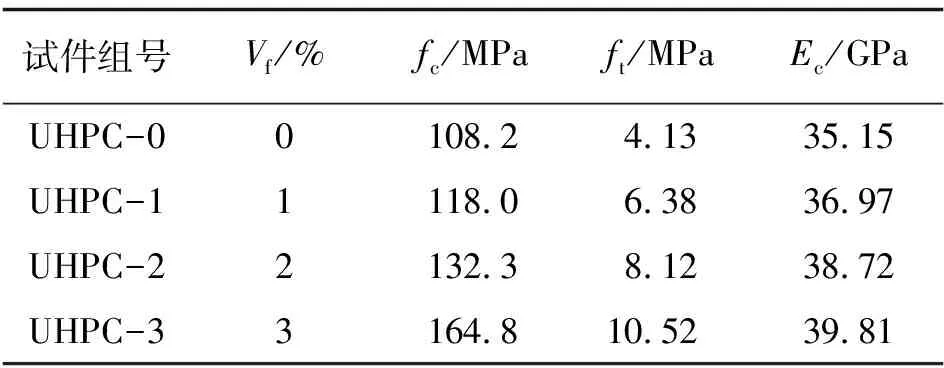
表2　UHPC力學性能

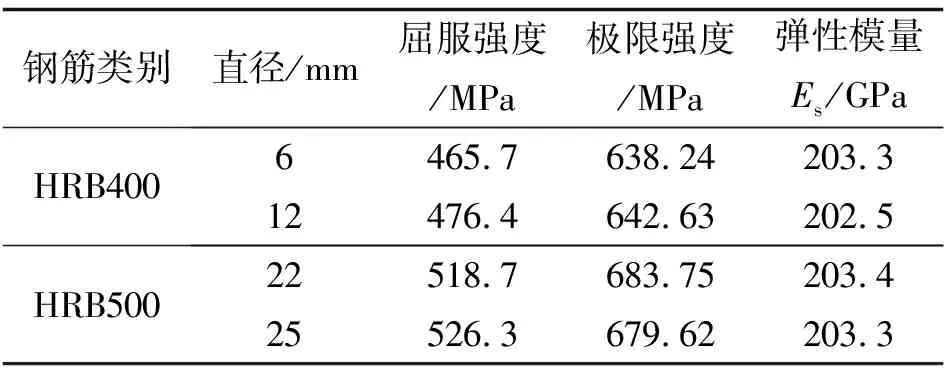
表3　鋼筋材性力學性能

2　試驗結果及分析

2.1　基本情況

圖3給出UHPC梁加載點的荷載-撓度曲線.其中UHPC梁的極限荷載是指荷載不能再繼續增加而梁撓度急劇下降時對應的荷載值.從圖中可見, UHPC梁的試驗過程分為彈性階段、 裂縫開展階段和屈服階段.

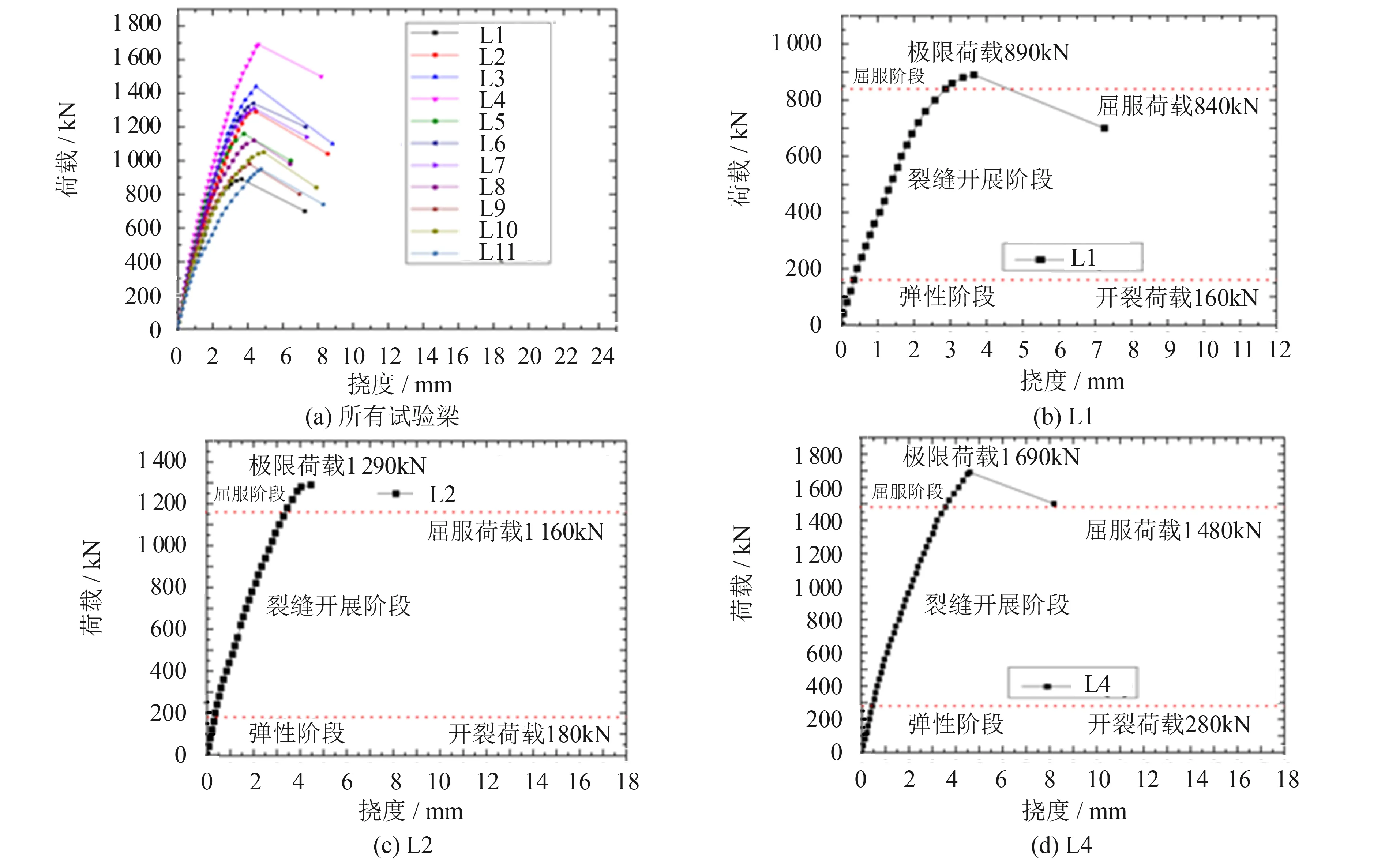
圖3　UHPC梁加載點荷載-撓度曲線Fig.3　Load-deflection curve at the loading point

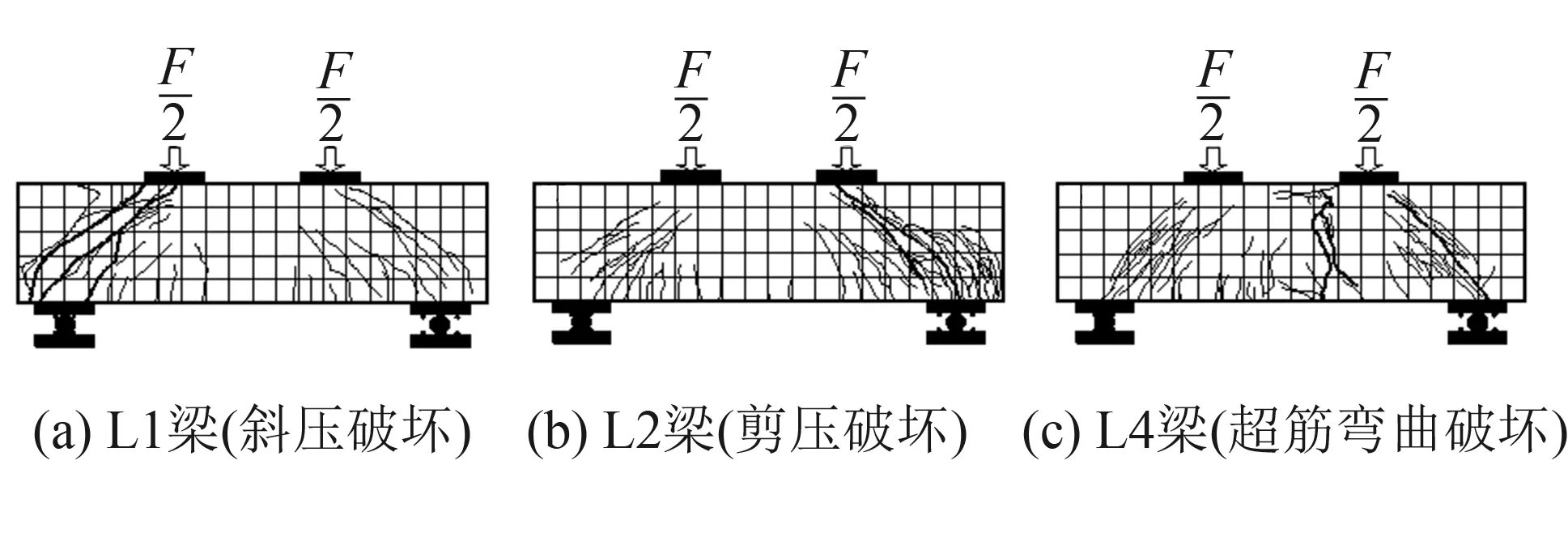
圖4　部分試驗梁裂縫分布圖Fig.4　Crack distribution of some test beams

圖4給出部分試驗梁裂縫分布圖.從圖中可以看出, 由于試驗參數的不同, 梁的破壞形態并不完全相同, 其中L1梁為斜壓破壞, L3、 L4梁發生了超筋彎曲破壞, 其余試驗梁均發生了剪壓破壞.L1梁試驗中, 荷載加載至160 kN (18%F)時, 在純彎區底部出現首條豎向裂縫, 裂縫寬度為0.06 mm； 荷載達到200 kN時, 梁腹部支座與加載點之間出現了斜裂縫, 隨著荷載的增加, 剪跨區出現一些幾乎平行的斜裂縫.而后, 支座與加載點處的裂縫從試驗梁腹部分別向加載點與支座處延伸.而純彎區的裂縫發展緩慢甚至停止發展.當荷載加載至840 kN (94%F)時, 梁進入屈服階段, 梁腹部混凝土被分割若干個條狀體, 當荷載加載至890 kN時, 條狀體的混凝土被壓碎且撓度急劇下降, 試驗中止, 中止時試驗梁主裂縫寬度為4.64 mm.該梁在破壞時呈現出明顯的脆性, 在工程設計中應避免這種破壞形式.

L2、 L5～L11等8根梁均屬于剪壓破壞, 這些梁所對應的極限承載力是本文要考察的抗剪極限承載力.以L2為例, 當荷載加載至180 kN (14%F)時, 在梁剪跨區底部出現首條彎曲裂縫, 裂縫寬度為0.04 mm； 隨著荷載的增加到220 kN時, 在剪跨區腹部出現首條斜裂縫, 隨著荷載的增加支座與加載點處的斜裂縫裂縫從試驗梁腹部分別向加載點與支座處延伸.當荷載加載至1 160 kN (90%F)時, 梁進入屈服階段, 密集的斜裂縫形成一條裂縫寬度明顯的臨界斜裂縫, 當荷載加載至1 290 kN時, 與臨界斜裂縫相交的箍筋發生屈服后, 臨界斜裂縫附近的混凝土被壓碎, 隨后試驗中止, 中止時試驗梁主裂縫寬度為2.14 mm.

L3和L4兩根梁出現超筋彎曲破壞.以L4為例, 當荷載加載至280 kN (17%F)時, 在梁腹板底部加載點處出現了首條彎曲裂縫, 裂縫寬度為0.06 mm； 當荷載加載至1 480 kN (88%F)時, 梁進入屈服階段, 在試驗梁頂部兩個加載點之間的混凝土被壓碎形成塑性鉸, 當荷載加載至1 690 kN時, 壓碎區由梁頂向梁底發展, 撓度急速下降, 試驗中止, 中止時試驗梁剪跨區斜裂縫的最大寬度為1.64 mm.

2.3　試驗參數分析

圖5給出不同參數下的荷載-加載點處撓度曲線.

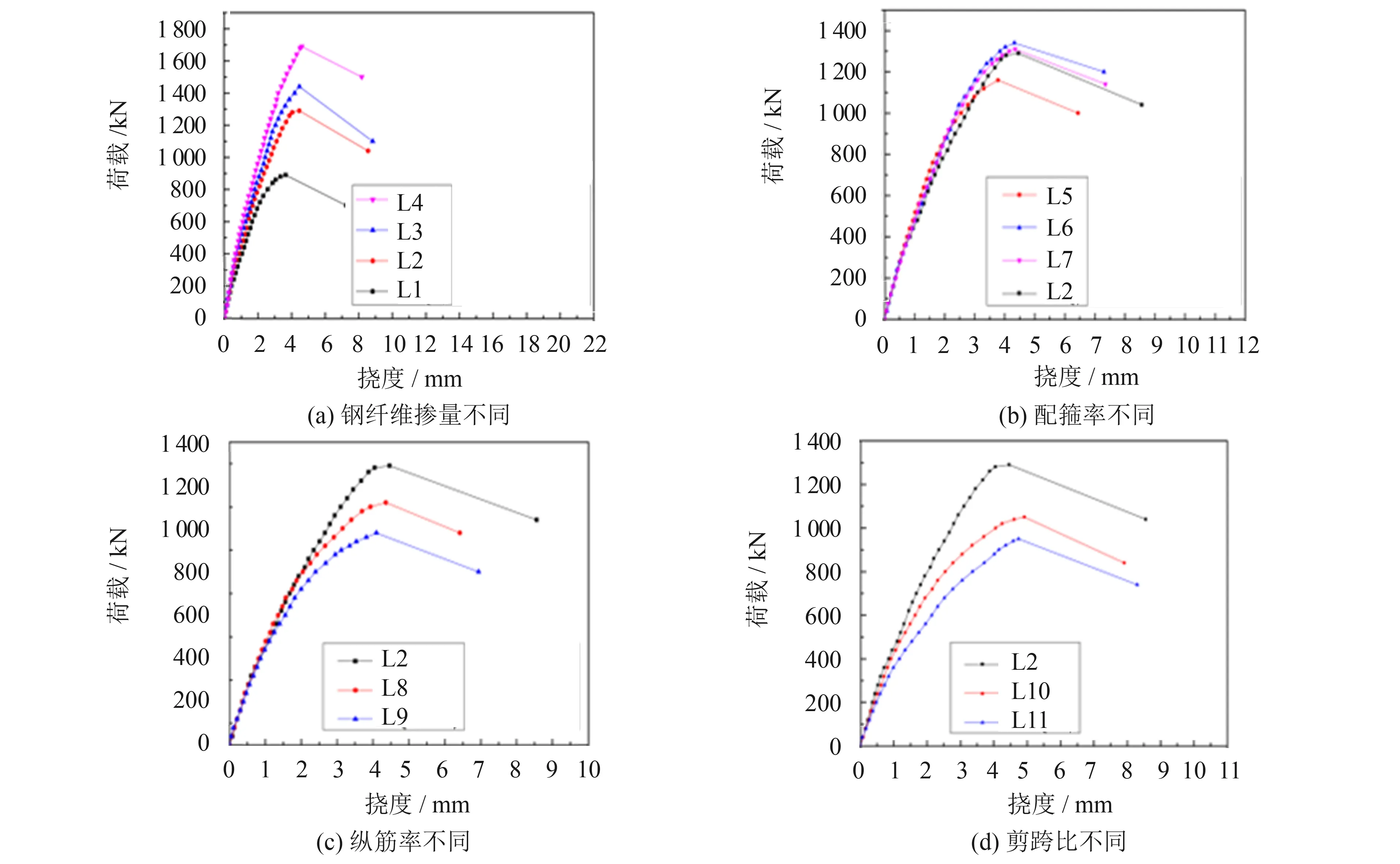
圖5　不同參數下的荷載-加載點處撓度曲線Fig.5　Load-deflection curve at the loading point under different parameters

1) 鋼纖維摻量.從圖5(a)可看出, 由于鋼纖維摻量的增加使得UHPC的受壓彈性模量增加, 從而提高了試驗梁的彎曲剛度和變形能力.L1～L4受剪極限承載力分別為445、 645、 720、 845 kN.對于發生受剪破壞的L1、 L2, 當鋼纖維摻量從0%增加到1%時試驗梁的受剪極限承載力增加了44.9%.L3、 L4發生彎曲破壞, 這說明鋼纖維摻量對梁的受剪承載力的影響大于受彎承載力.梁開裂前由于鋼纖維與UHPC細骨料之間的咬合作用, 使得UHPC的抗裂能力增強(見表1).在實際工程中, 雖然增加鋼纖維摻量可提高梁的抗剪承載力, 但不應摻入過多的鋼纖維以防止超筋破壞.

2) 配箍率.從圖5(b)可看出, 配箍率的增加并不能提高梁的剛度, 但可提高試驗梁極限承載力和極限撓度.L5、 L2、 L6、 L7受剪承載力分別為580、 645、 655、 670 kN.與不配箍筋的L5相比, 配箍筋的L2的極限受剪承載力明顯提高, 但增加配箍率對梁極限承載力提高不明顯.

3) 縱筋率.從圖5(c)可看出, L9、 L8、 L2受剪承載力分別為490、 560、 645 kN.試驗梁的開裂荷載和極限荷載均隨著縱筋率的增大而增大, 這是由于鋼纖維的存在增強了縱筋的銷栓作用.

4) 剪跨比.從圖5(d)可看出, 當梁進入裂縫開展階段后, 撓度隨著剪跨比的增加而增加.L2、 L10、 L11受剪承載力分別為645、 525、 475 kN, 試驗梁的受剪承載力隨著剪跨比的增大而減小.在普通混凝土梁中認為當剪跨比λ<1.5時, 剪跨比對梁受剪承載力無影響, 當1<λ<3時普通混凝土梁發生剪壓破壞.而在UHPC梁中當剪跨比λ<1.5時, 剪跨比增加對試驗梁承載力仍有明顯的影響, 鋼纖維摻量為0%的L1(λ=1.2)發生斜壓破壞, 說明影響UHPC梁受剪破壞形態的剪跨比范圍可能與普通混凝土梁不同.

3　UHPC梁抗剪承載力計算方法

圖6　試驗梁破壞形式Fig.6　Failure mode of beam

對UHPC梁抗剪公式的推導是根據普通混凝土梁的抗剪理論而來, 但由于忽略了UHPC本身的抗拉強度, 導致計算結果離散性較大低估了UHPC梁的受剪承載力, 無法為工程設計提供參考.文獻[6]基于桁架-拱模型, 通過UHPC梁的受剪機理分析, 提出考慮UHPC的抗拉作用的受剪承載力計算公式, 計算結果與收集到的UHPC梁的受剪試驗結果吻合較好.本試驗中, 發現模型梁的破壞模式符合桁架-拱模型, 如圖6所示.故本文選擇文獻[6]的受剪承載力計算公式為基本公式, 根據本文試驗結果進行進一步改進.由文獻[6]可知：

桁架模型承擔的剪力：

Vtr=(ρsvfyv+σt)bwzcotθ

(1)

桁架模型中斜壓桿的壓應力：

σc=(ρsvfyv+σt)(1+cot2θ)

(2)

UHPC富余強度：

σa=vfc-cos(θ-φ)σc

(3)

拱模型承擔的剪力：

Vac=σabwh0cos2θtanφ

(4)

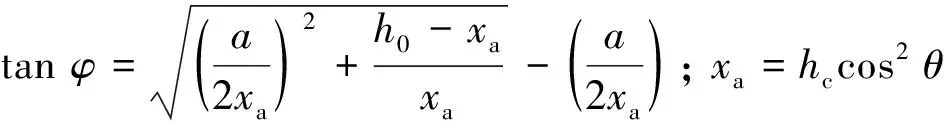
UHPC的抗剪承載力：

V=Vtr+Vac

(5)

圖7　抗剪承載力計算值與試驗值對比Fig.7　Comparison between test result and calculated result

將試驗中發生剪壓破壞的試驗梁、 文獻[6～8]共74根UHPC梁的試驗值與通過文獻[6]計算得到的計算值進行對比分析(見圖7), 計算值與實驗值比值的平均值為0.96, 標準差為0.16.

根據試驗結果, 對文獻[6]提出的公式進行如下的改進：

1) 從上節的分析可知縱筋率對UHPC梁受剪承載力有影響, 根據文獻[9]將桁架模型中斜裂縫區域內梁橫截面混凝土的實際有效受壓區截面積取為Ae=ηbwz, 將其影響考慮到式(2)中, 則有：

桁架模型中斜壓桿的壓應力：

(6)

其中:η為考慮縱筋對UHPC的約束作用, 根據文獻[9],η=0.89, 本文為方便計算取η=0.9.根據文獻[6]取θ=45°, cos(θ-φ)=0.9.

將式(6)代入式(3)中求得σa后, 將σa代入式(4), 最后求得UHPC的受剪承載力為：

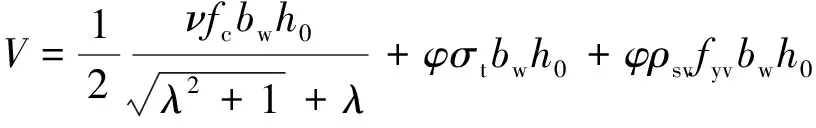
(7)

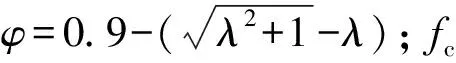
2) 在荷載作用下, 梁腹部UHPC處于二軸拉、 壓應力狀態, 同普通混凝土一樣會發生軟化現象, 使得復合應力狀態下的UHPC抗壓強度降低, 一般通過軟化系數v來考慮UHPC的強度降低.軟化系數v一般是通過收集試驗值進行擬合.文獻[6]收集了51根梁, 擬合得到UHPC的軟化系數取0.7.本文收集共74根梁進行擬合得到UHPC的軟化系數取v=0.65.

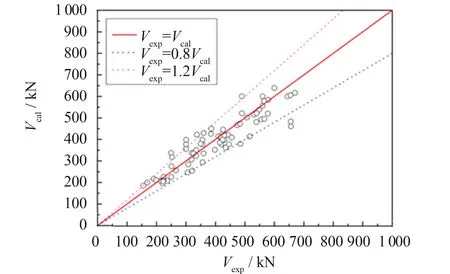
圖8　修正后的抗剪承載力計算值與試驗值對比Fig.8　　　　Comparison between test result and calculated result by proposed method

3) 文獻[6]中剪跨比的取值范圍是根據普通混凝土來取的, 而在普通混凝土梁中剪跨比的范圍為1.5≤λ≤3, 對于本文中的8根發生剪壓破壞且剪跨比λ=1.2與λ=1.4的試驗梁, 采用文獻[6]計算的計算值會小于試驗值.故本文對式(7)中的λ的適用范圍進行調整： 對UHPC梁受剪承載力公式中剪跨比的范圍取為1.2≤λ≤3, 當λ>3時, 取λ=3; 當λ<1.2時, 取λ=1.2.

對修正后的式(7)進行驗證, 驗證結果見圖8.計算值與實驗值比值的平均值為0.99, 標準差為0.13.相對于文獻[6]的計算方法, 本文的UHPC梁受剪承載力計算方法的準確性與適用性進一步提高, 可為UHPC梁的工程設計提供參考.

4　結語

1) UHPC梁的受剪承載能力隨著鋼纖維摻量、 縱筋配筋率、 配箍率的增加而提高, 隨著剪跨比的增加而降低.對梁受剪承載力影響最大的是鋼纖維摻量, 其次為剪跨比、 縱筋率, 最小的是配箍率.

2) 鋼纖維摻量的增加明顯提高梁的抗彎剛度和變形能力, 鋼纖維摻量的變化會導致試驗梁破壞形態的變化.

3) 對目前UHPC梁抗剪計算方法中適用性較好的算法進行修正.按該公式計算得到的計算值與試驗值比值的平均值為0.99, 標準差為0.13, 實驗值與計算值吻合良好, 可為UHPC梁的工程設計提供參考.