基于改進RRT算法的移動機器人路徑規劃
金丹
(上海海事大學信息工程學院,上海 201306)
0 引言
機器人學一直是科學技術研究領域的熱點問題,它集中了多種尖端學科最先進的研究成果。隨著社會的發展與科技的進步,機器人的應用已經越來越普遍了,其中移動機器人的使用更是受到人們的青睞。路徑規劃問題是移動機器人研究中的一個重要環節,它的目的是使移動機器人自主并且安全地從初始位姿移動到目標位姿。前人在路徑規劃方面的研究已經有了顯著的成效,但仍有一些算法上的不足。本文所研究的快速擴展隨機樹(Rapidly-exploring Random Tree,RRT)是一種數據結構和算法[1],通過隨機地并且增量式地在狀態空間中生成采樣點,快速有效地搜索高維空間,把搜索方向導向空白區域[2-3],這些特點使得它在路徑規劃方面有良好的應用前景與深入的研究。針對其搜索過于平均,規劃路徑非最優等缺陷,對基本快速擴展隨機樹算法加以改進,引入Dijkstra算法,實現了移動機器人最優路徑的規劃。
1 基本RRT算法及其改進原理
機器人的路徑規劃[4-5]問題被定義為:給定機器人在運動區域的初始位姿qinit和終點位姿qgoal找到一條路徑,即一個位姿的連續序列,使得機器人沿著該路徑能夠從初始位姿運動到終點位姿,且在移動的過程中不與環境中的任何障礙物發生碰撞。路徑規劃示意圖如圖1所示。圖中灰色的部分都是障礙物區域,白色的部分是機器人可以自由移動的無障礙區域,帶有箭頭的曲線便是一條從初始節點qinit到目標節點qgoal的路徑。
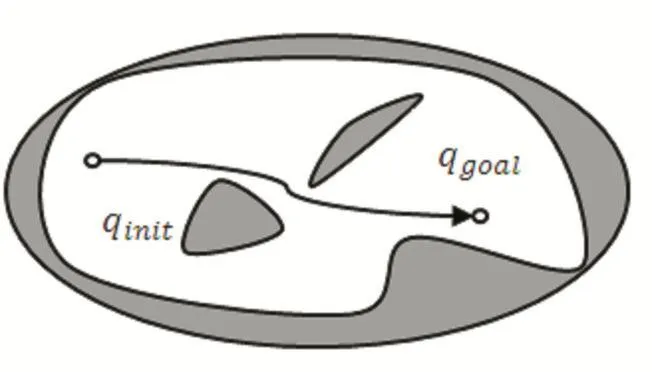
圖1 路徑規劃示意圖
1.1 基本RRT算法原理
快速擴展隨機樹是一種常見的用于機器人路徑規劃的方法,本質上是一種隨機生成的數據結構——樹。它遵循控制理論的系統狀態方程,以初始點為樹的根節點,在控制量的作用下增量式地產生一條從初始狀態到新狀態的隨機樹,當隨機樹中的葉節點中包含了目標點或者目標區域時,說明在隨機樹中找到了一條從根節點到目標點的路徑。RRT的擴展方式如圖2所示。

圖2 RRT擴展過程
在快速擴展隨機樹中,qinit表示根節點(初始節點),qrand表示隨機節點,qnear表示隨機樹中離qrand最近的節點,在qnear和qrand的連線上以一定的步長λ為單位長度獲取一個新節點qnew,然后通過碰撞檢測,以確保從qnear到qnew這一小段都不與任何障礙物發生碰撞,則qnew就是擴展的新節點加入到隨機樹中,反之則需要重新尋找一個適合的新節點繼續擴展隨機樹。重復以上步驟,直至qnew到達目標點或者目標區域算法結束,此時便在樹中找到一條從起始節點到目標節點的路徑。
1.2 改進RRT算法原理
RRT算法相對于其他算法而言,在搜索效率方面已有很大優勢,在理論上總能找到一條可行路徑,但是仍有需要改進的地方。由于其擴展的新節點是在運動區域中隨機產生的,覆蓋的區域過于平均,在產生的冗余點上有一定的耗時,同時規劃出來的路徑質量不高,往往與最短路徑的差距較大。
為了提高路徑規劃的質量,減少移動機器人移動過程中消耗過多的時間,更安全高效地避開障礙物,此處借助于Dijkstra算法。
Dijkstra算法是最早用于機器人路徑規劃的一種算法,它致力于規劃出一條移動代價最小的路徑。它應用了貪心算法的模式,是目前公認的最好的求解最短路徑的方法。此算法具有設計思路簡單、分析速度快、工程實現能力強、通用性強等優點,其主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。針對上述RRT算法的缺陷,引入Dijkstra算法[6-8],用于處理移動機器人路徑規劃問題的RRT樹形結構生成后的軌跡尋優問題。RRT算法與Dijkstra算法的結合,在程序搜索之前判斷路徑規劃的約束條件,不符合約束條件的節點和邊都去掉,大大的降低了遍歷的節點和邊的個數,這樣Dijkstra算法的搜索效率在RRT的基礎上有了明顯提高,從而更快地找到一條最短路徑的最優解[9]。
2 RRT算法改進前后對移動機器人路徑規劃的研究
移動機器人的路徑規劃要滿足路徑上的權重系數盡量小,根據不同的環境情況需要選擇其合適的拓展步長來滿足最優路徑規劃的要求,使其在移動的過程中盡量符合約束條件的要求。RRT算法在狀態空間中完成樹形結構圖擴張后得到的可行路徑,僅能作為移動機器人路徑規劃中的一條通路,但仍未達到最優的要求。在移動機器人的作業過程中,達到最優規劃是基本的需求,可以大大地減少機器人能量的消耗,提高機器人的工作效率。
下面歸納RRT算法的構建過程:
第一步:初始化起始節點qinit和目標節點qgoal,并將起始節點qinit作為快速擴展隨機樹T的根節點qroot,初始化快速擴展隨機樹T;
第二步:判斷|qinit-qgoal|≤λ,且用碰撞檢測函數collision(qinit,qgoal)判斷這一段(qinit,qgoal)路徑是否不與障礙物發生碰撞,若是,轉到第八步,若不是,轉到第三步;
第三步:生成隨機點qrand;
第四步:在隨機樹T中找到離qrand最近的點qnearest;
第五步:在qnearest到qrand的連線上取一個新的節點qnew作為T擴展的新節點,使dis( )qnearest,qnew=λ,并且(qnearest,qnew)這段路徑不與障礙物發生碰撞,若存在這樣的qnew,轉到第六步,若不存在,轉到第三步;
第六步:將新節點qnew添加到隨機樹T中;
第七步:判斷|qnew-qgoal|≤λ,若是轉到第八步,不是,轉到第三步;
第八步:返回獲得的從起始點qinit到目標點qgoal的路徑;
第九步:結束。
在RRT算法上引入Dijkstra算法對其加以改進,解決最短路徑的尋優問題,其核心思想是通過計算RRT算法提供的節點來規劃可通的路徑,并且通過搜索找到最短的路徑。可以解釋為是在RRT算法已經找到可通路徑的基礎上,利用Dijkstra算法對擴展的隨機樹進行二次重采樣,將可通路徑調整為最短路徑。但是增加Dijkstra算法后會增加路徑規劃時間,所以需要在多次仿真實驗中獲得合適的參量條件,減少Dijks?tra算法遍歷的次數,達到路徑最優與時間消耗相協調。改進后的算法是在RRT算法的第七步后調用Di?jkstra算法,所得路徑的總代價值costdijk<costrrt,則更新路徑,將新路徑作為最優解。
3 RRT算法改進前后在MATLAB下仿真結果
按照以上原始的RRT算法及其改進后的算法步驟,在MATLAB的仿真環境用代碼實現以上的理論結果,為了使實現的結果更具有說服性和可靠性,本次程序考慮在多種環境下執行仿真實驗。所有圖的尺寸設為500×500,圖中的起始節點坐標設為(10,10),目標節點坐標設為(490,490),起始節點和目標節點的選擇不是唯一的,視仿真情況而定。隨機樹的擴展步長設為20,此步長是在不斷地實驗過程中選擇的較為合適的步長,從而不會因為步長的選擇不當影響程序的效果,好的步長的選擇可以起到很大的作用。圖中黑色的區域設為障礙物,作為移動機器人移動過程中的威脅源,通過碰撞檢測函數使移動機器人在移動的過程中避開威脅源,成功的從起始節點到達目標節點。仿真結果的前后對比圖如圖3-5所示。圖中藍色的路徑為原始RRT算法實現的結果,紅色的路徑為改進后RRT算法實現的結果。
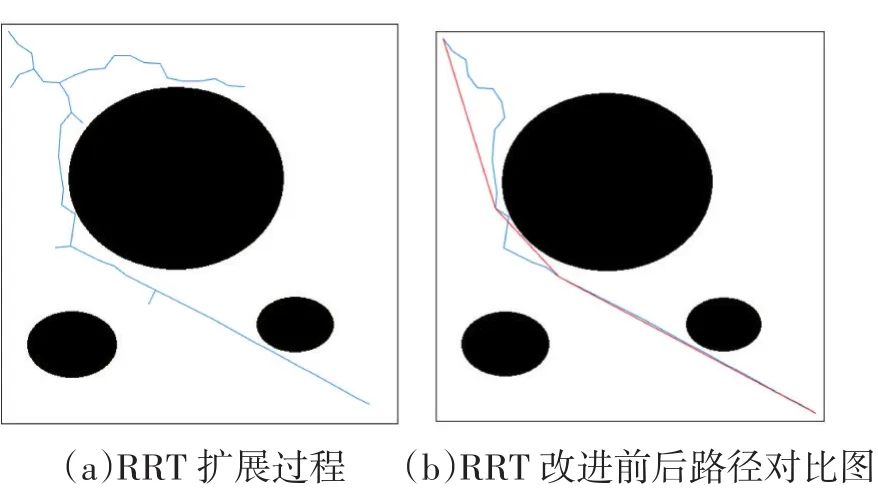
圖3 簡單障礙地圖環境
從圖3中可以看出在簡單障礙地圖環境中,相對于原始RRT算法規劃出來的路徑而言,改進后的RRT算法規劃出來的路徑達到最優。仿真數據顯示,原始RRT規劃的路徑長度是7.528023e+02,執行時間是1.479903e+01s,改進后的RRT算法規劃的路徑長度是7.194621e+02,執行時間為2.189992e+01s,可見在時間消耗上并沒有很大差距,也達到了路徑的最優化。
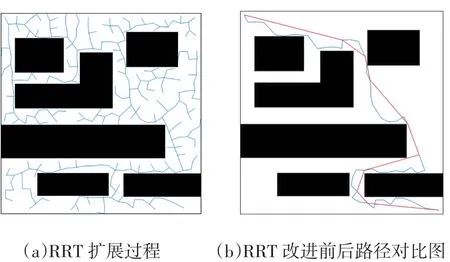
圖4 狹窄通道地圖環境
從圖4中可以看出在狹窄通道地圖環境中,相對于原始RRT算法規劃出來的路徑而言,改進后的RRT算法規劃出來的路徑達到最優。仿真數據顯示,原始RRT規劃的路徑長度是1.264349e+03,執行時間是5.700553e+02s,改進后的RRT算法規劃的路徑長度是1.012422e+03,執行時間為5.736099e+02s。相對于圖4的環境,此處地圖相對復雜有難度,RRT算法的搜索節點較多,搜索過于平均,但在時間的消耗上依然得到了控制,同時達到了路徑的優化。
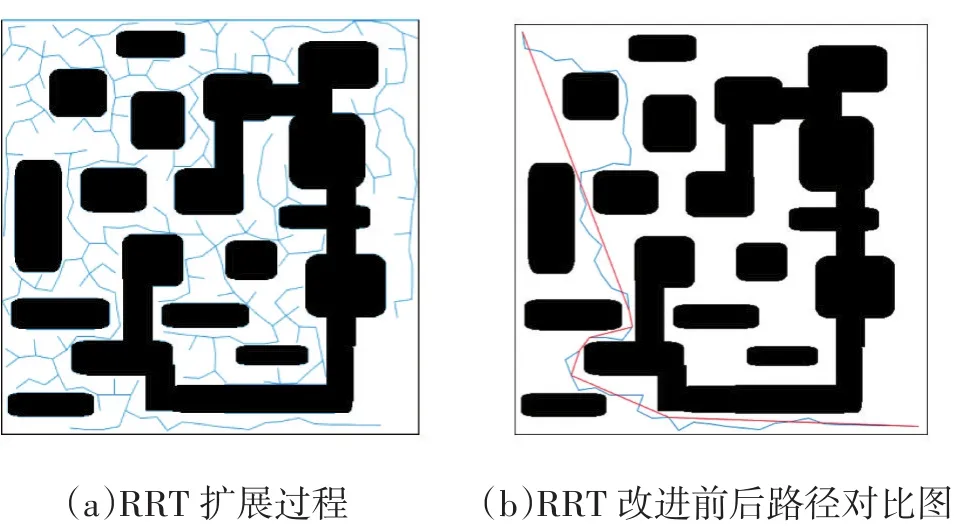
圖5 復雜障礙地圖環境
從圖5中可以看出在復雜障礙地圖環境中,相對于原始RRT算法規劃出來的路徑而言,改進后的RRT算法規劃出來的路徑達到最優。仿真數據顯示,原始RRT規劃的路徑長度是1.144686e+03,執行時間是6.751927e+01s,改進后的RRT算法規劃的路徑長度是9.200832e+02,執行時間為1.089810e+02s,這里的環境近似于一個迷宮,地形復雜,可通的路徑有待搜索,但在原始RRT算法的基礎上,改進后的算法依然達到了預期的效果,實現了在路徑和時間上平衡的要求。可見在復雜的地圖環境下依然可以很好地實現。
4 結語
本文主要的目的是為了實現移動機器人的最優路徑的規劃,使其在移動的過程中成功地避開障礙物的威脅,通過最短的路徑,并且實現消耗的時間最少的效果。以目前熱門的高效搜索RRT算法為基礎,選擇一種最短路徑搜索Dijkstra算法加以改進,充分利用兩種算法的優點。在MATLAB仿真環境下,將改進前后的RRT算法進行對比,比較改進前后實現的效果。仿真結果顯示,改進后的算法比原始算法在性能上有了明顯的優化,與此同時,也使用各種不同的地圖環境驗證了算法高效性和可靠性,在時間和路徑兩方面達到了很好的均衡,即時間消耗未增加過多,但路徑達到最優。

