測試生產中不同滲流機理下油氣井出砂量分析
姜海龍
(西安石油大學機械工程學院,陜西西安 710065)
油氣藏流體進入井筒,孔隙壓力從外邊界到井壁處為一個下降的壓力剖面[1]。由于流體與飽和流體的多孔介質巖石之間的相互作用,孔隙壓力的變化會導致地層井壁應力和有效應力的變化,可能導致裸眼井壁出砂,若出砂量太大,可能導致生產井的報廢[2]。油氣藏開發和測試過程中不同滲流模型對應的近井地層孔隙壓力梯度不同,特別是對于高壓氣藏,滲流速度足夠大時滲流模型中要考慮加速效應,而考慮加速效應滲流模型在近井地層孔隙壓力梯度非線性甚至可能無窮大并且流體質量流量存在一個最大值[3-5],進而改變近井地層巖石的有效應力狀態。目前,油氣藏開發和測試過程,井壁圍巖受到Darcy、非Darcy滲流的影響,很多學者對地層出砂問題進行了研究,但沒有涉及考慮加速效應滲流作用和出砂量計算[6-9]。另一部分學者,僅僅分析了測試生產中油氣藏的滲流特征,但沒有聯系井壁坍塌[3-5,10-13]。金衍等[14]研究了考慮加速效應滲流模型的井壁圍巖徑向應力,但沒有涉及周向應力分析和出砂量計算。Wu等[15]和Papamichos等[16]通過實驗研究認為井眼坍塌的破壞形狀一般呈橢圓形,但對于滲流作用和出砂量計算問題,沒有給予討論和研究。姜海龍等[17-20]分析了生產時高壓氣井裸眼段井壁穩定性和近井應力狀態,但沒有涉及出砂量的計算。在上述研究基礎上,本文從力學機理出發,從相態、滲流模型、地應力三方面分析了徑向滲流作用下直井近井地層巖石應力狀態,并結合莫爾庫倫準則,對油氣藏開發和測試過程中裸眼井壁儲層段的坍塌區域形狀和出砂量進行了分析和預測。
1 井壁圍巖應力狀態
油氣藏開發過程中井壁周圍地層應力受到遠場地應力和地層流體壓力分布的影響。假設遠場地應力為σr0,遠場地層流體壓力為 P0,將文獻[2]中方程(4.51)、(4.52)和(4.53)無量綱化得到[14]:
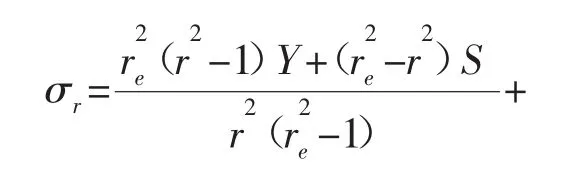
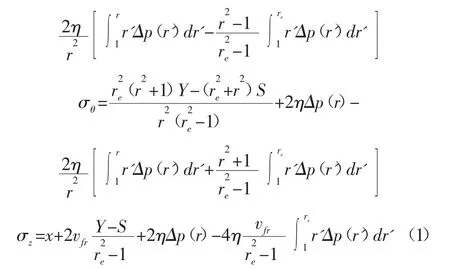
以下所有的變量都為無因次變量,因此井壁圍巖有效應力為:
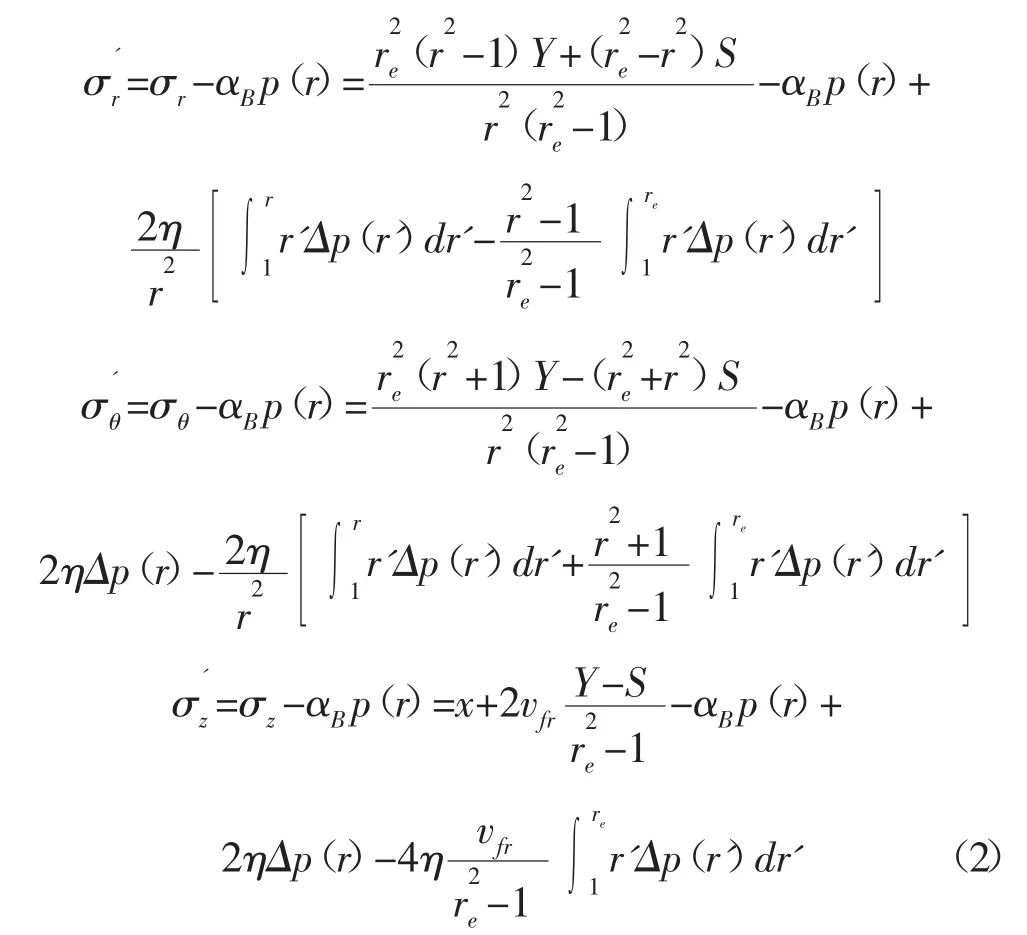
假設巖石破壞遵循莫爾-庫倫準則[2],用有效應力可表示為:
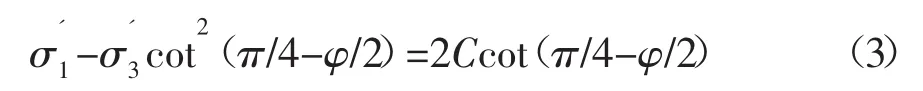
2 均勻地應力場油藏出砂量分析
液體達西滲流模型時流體壓力分布為[14]:
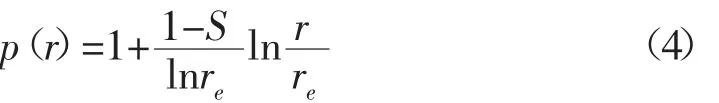
有效周向應力為:
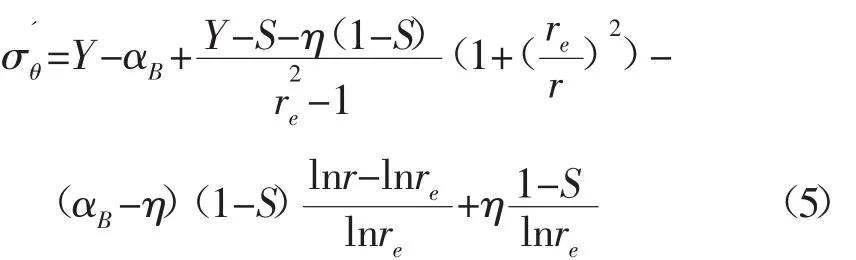
有效周向應力的導數為:
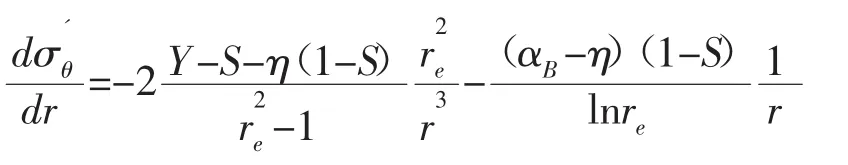
因為 0<S<1,0<η<0.5,Y>1,則有:
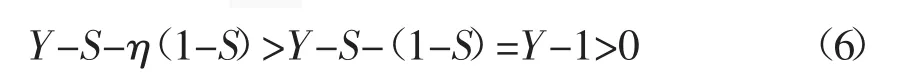
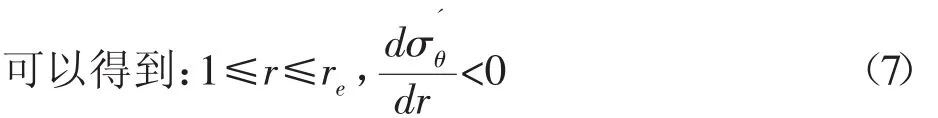
有效徑向應力的導數為:
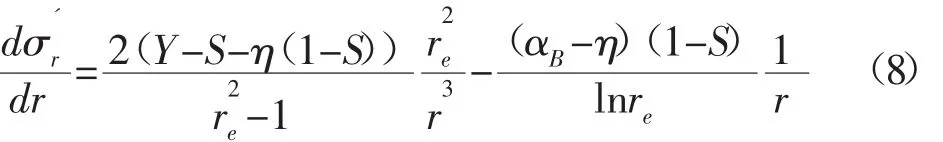
則存在這樣一個ra[14]:
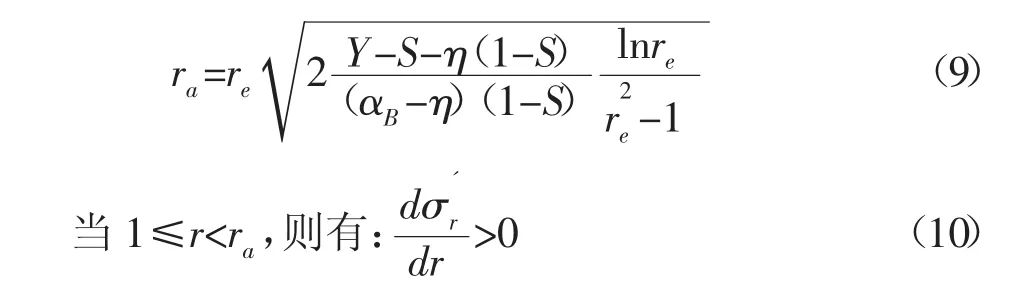
因為 0<φ<π/2,則有 cot2(π/4-φ/2)>0,結合式(7)和式(8),則式(3)左邊部分的導數:
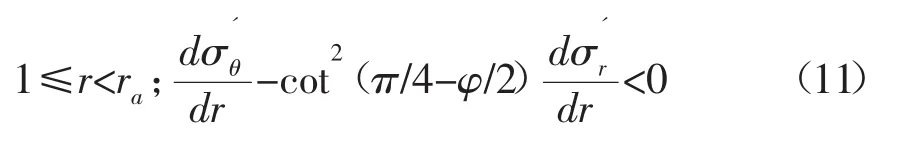
根據式(3)和式(11),可以看出坍塌最先出現在井壁,并且當井壁圍巖應力達到坍塌臨界狀態時,在r>1的近井地層坍塌停止,不再發展。
3 均勻地應力場氣藏出砂量分析
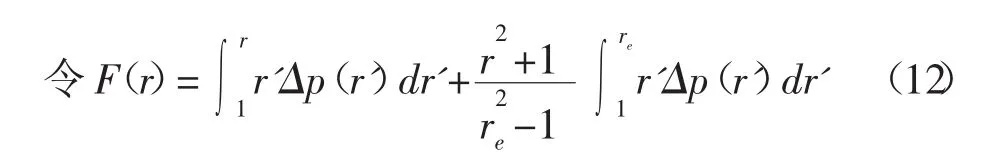
F(r)具有以下關系:
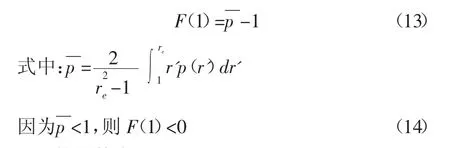
F(r)的導數為:
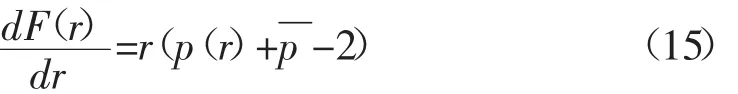
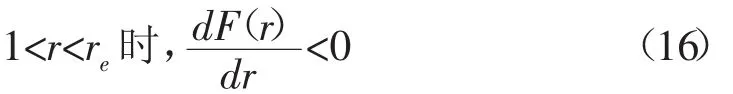
結合式(14),可以得到:

有效周向應力導數為:
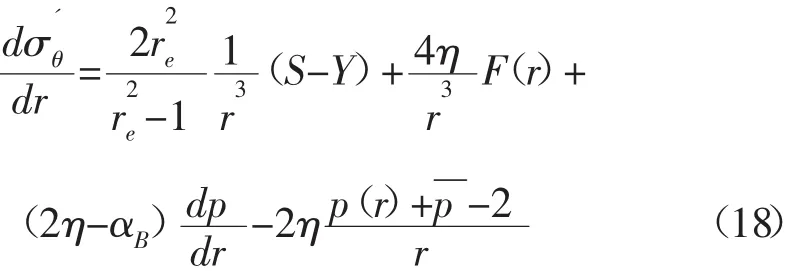
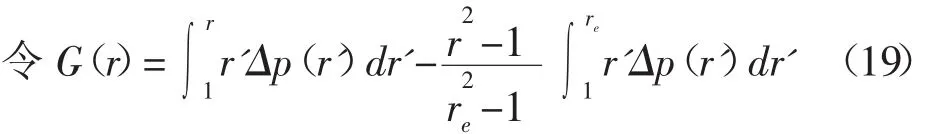
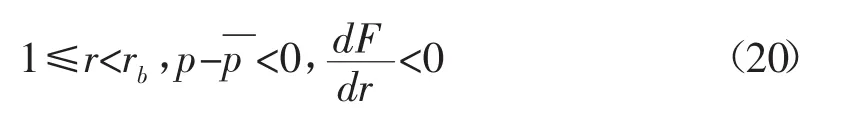
有效徑向應力導數為:
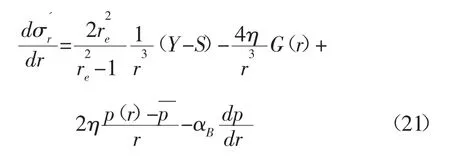
為了分析方便,取φ=π/6,則式(3)左邊部分的導數為:
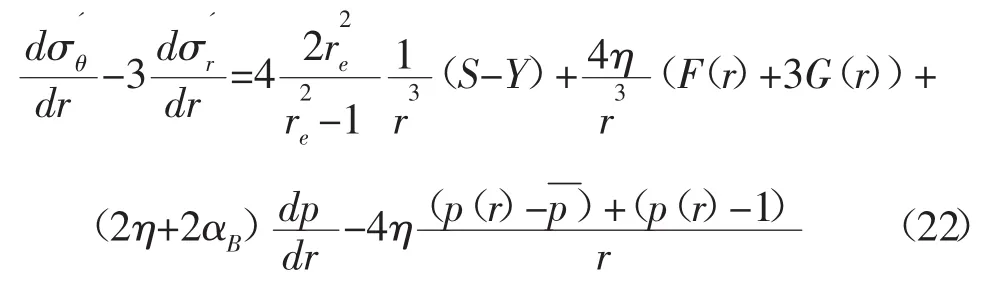
氣藏試氣或生產過程中,氣體的運動方程可能為Darcy滲流模型、Darcy-Forchheimer滲流模型和考慮加速效應的滲流模型,這三種滲流作用下近井地層巖石有效徑向應力可能為負值,只要滿足式(23):

Darcy滲流模型、Darcy-Forchheimer滲流模型和考慮加速效應的滲流模型在質量流量相同的情況下,孔隙壓力梯度具有式(24)關系[4]:

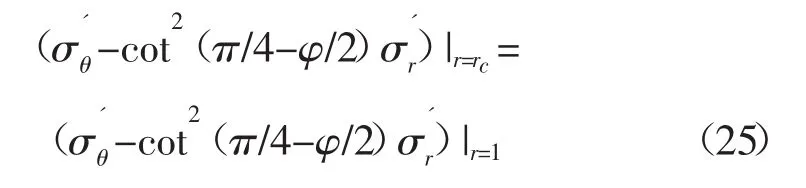
因此當井壁(r=1)的有效周向應力和有效徑向應力滿足式(3)時,即井壁圍巖應力達到坍塌臨界狀態,坍塌并不停止,在1<r≤rc區域內,坍塌繼續發展。
因此式(25)是否存在或者說坍塌是否繼續發展的條件為:
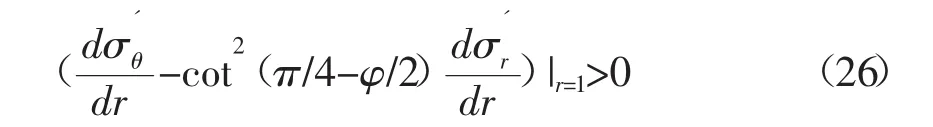
高壓氣藏直井無因次出砂量V1為:

根據式(2),得:
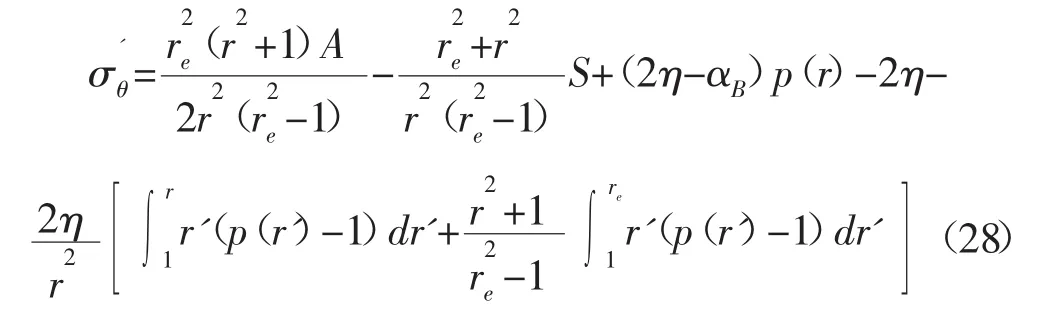
則三種滲流模式對應的有效周向應力在1≤r<re范圍都有:

而有效徑向應力在近井地層有:
則近井地層有:

由式(32)可以看出,考慮加速效應滲流模型對應的井壁圍巖應力最先達到臨界坍塌條件。三種滲流模型孔隙壓力梯度為[14]:
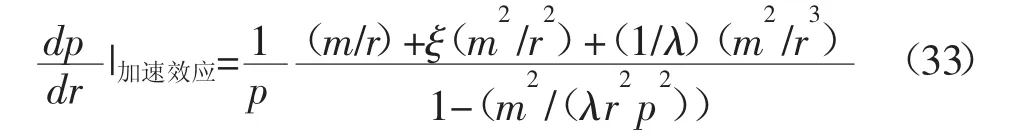
式中:ξ-Darcy-Forchheimer阻力系數;λ-表征加速效應的因子,λ→∞和ξ=0為Darcy模型,λ→∞和模型。
當 m=0.065,Y=1.1,re=2 000,η=0.5,φ=π/3,C=0.154,αB=1時,Darcy滲流作用下的近井地層巖石應力狀態(見圖1),可以看出近井地層存在一個坍塌區域(1≤r<rc),此時 rc=1.005 5,很顯然坍塌區域邊界為一圓形,無量綱的出砂量V1為0.034 7。
當 m=0.041,Y=1.1,re=2 000,η=0.5,φ=π/3,C=0.143 9,αB=1;λ=0.5,ξ=100 時,三種滲流模式作用下的近井地層巖石應力狀態對比(見圖2和圖3),井壁圍巖應力差在Darcy滲流和Darcy-Forchheimer滲流作用下分別為1.044 3和0.609 6,而考慮加速效應滲流模型作用下的井壁圍巖應力差最大為1.074 0,說明考慮加速效應滲流模型對應的井壁圍巖應力最先達到臨界坍塌條件;可以看出同樣質量流量下,考慮加速效應滲流模型對應的出砂量最大,rc=1.138 7,由式(27)得到無量綱出砂量V1為0.931 9。
4 非均勻地應力場氣藏出砂量計算
假設地層是均勻各向同性、線彈性多孔材料,并認為井壁圍巖處于平面應變狀態,水平最大地應力σH,水平最小地應力σh。在式(2)的基礎上,根據彈性力學理論得到滲流作用下井壁圍巖有效應力為:
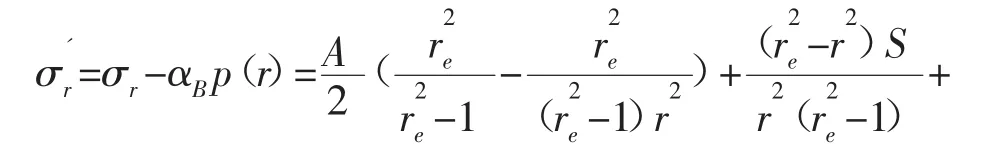
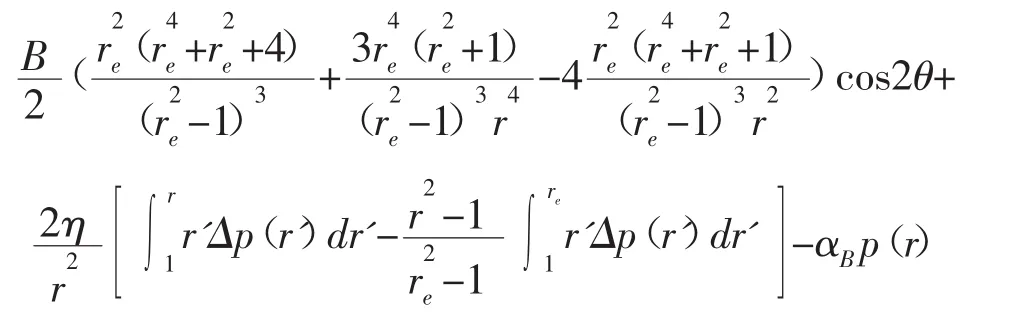
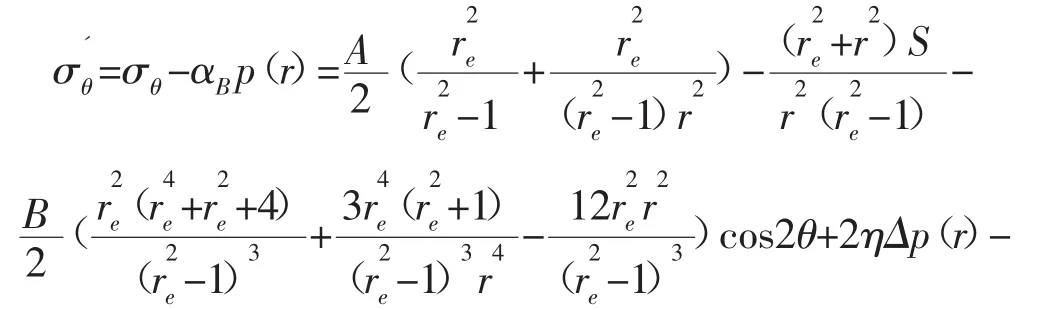
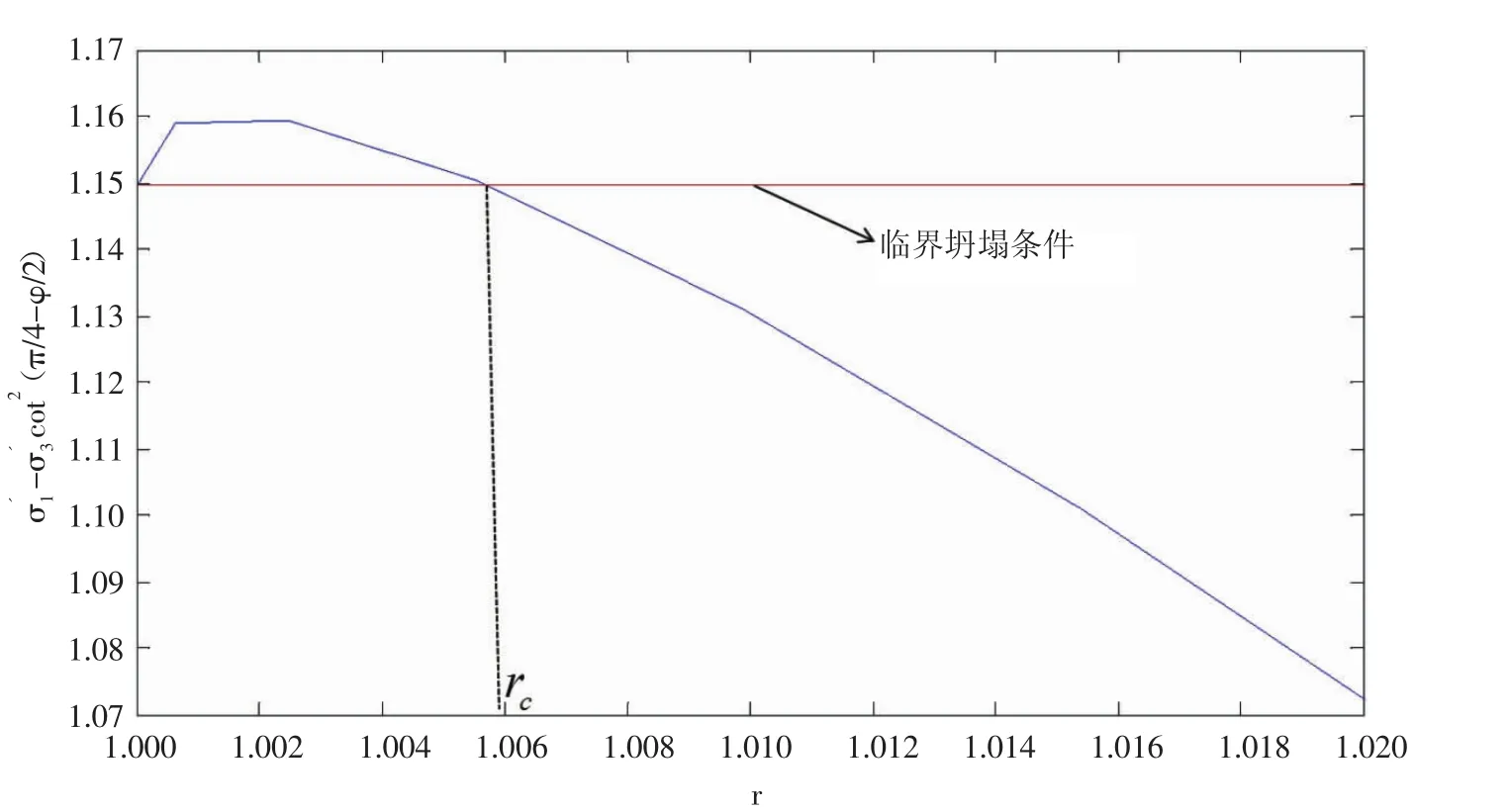
圖1 Darcy滲流作用下井壁達到臨界坍塌狀態時地層巖石應力狀態
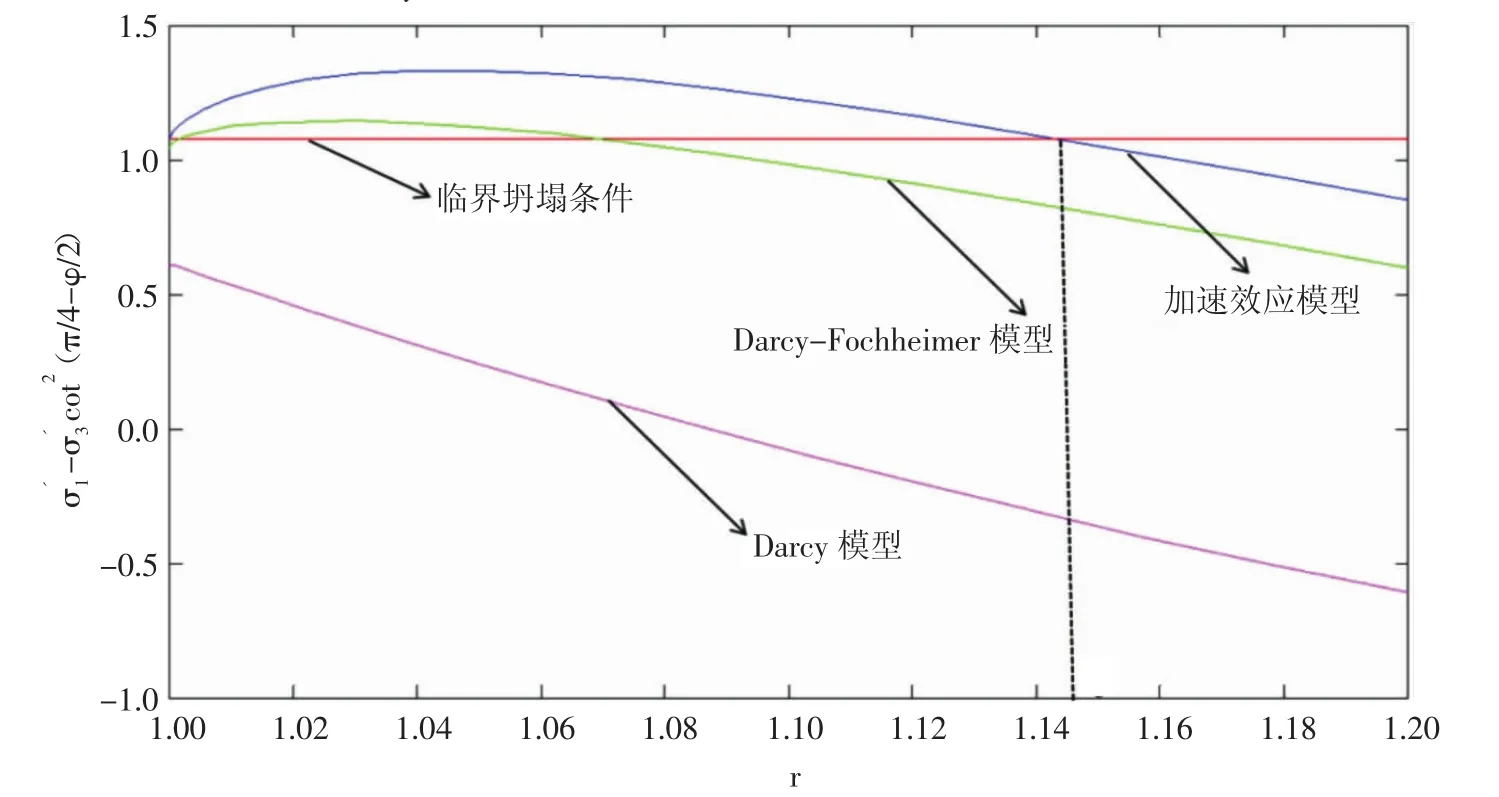
圖2 考慮加速效應滲流作用下井壁達到臨界坍塌狀態時不同滲流模型對應的地層巖石應力狀態對比
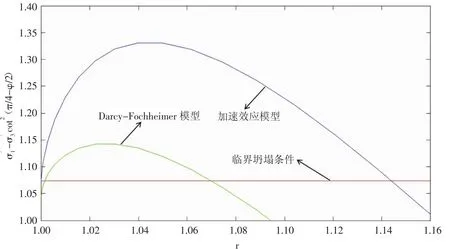
圖3 考慮加速效應滲流作用下井壁達到臨界坍塌狀態時不同滲流模型對應的地層巖石應力狀態對比(圖2的放大圖)
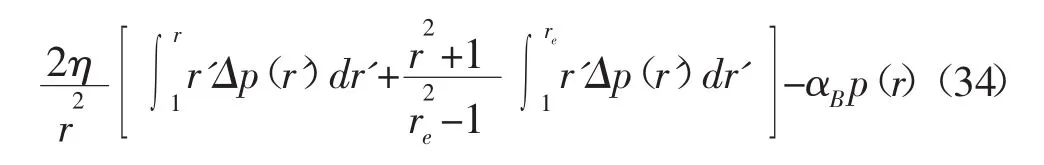
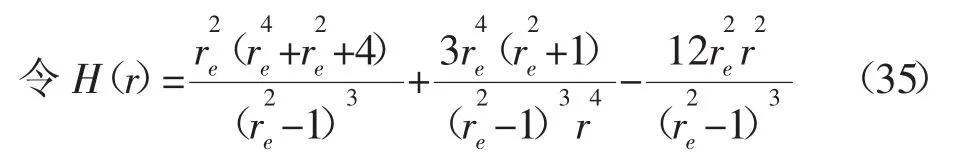
當 1≤r≤re時,,則有:
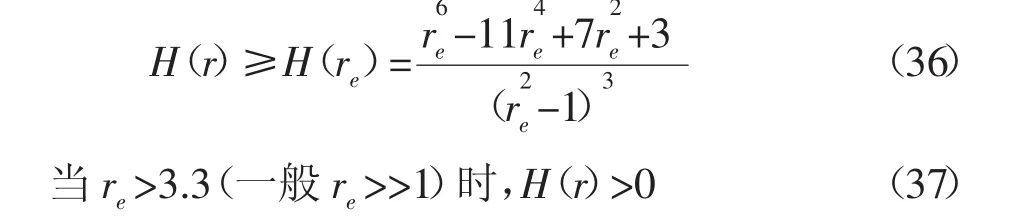
可以看出σ'θ最大水平地應力方向上最小,而在最小水平地應力方向上最大。
將式(34)代入式(3)中,則式(3)左邊部分(r=1,αB=1)為:
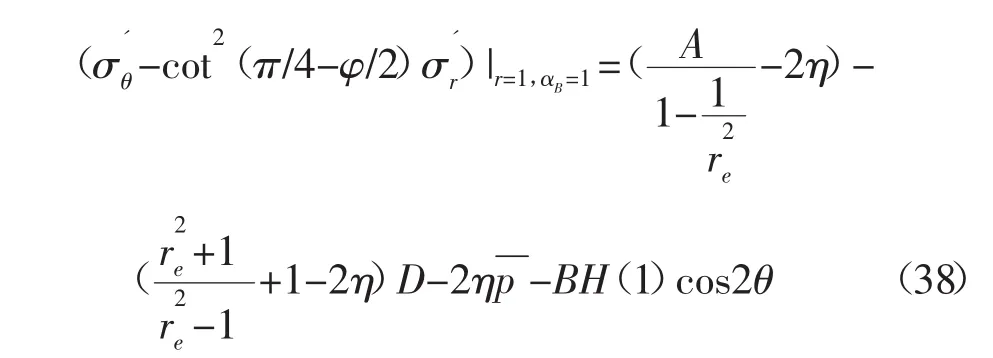
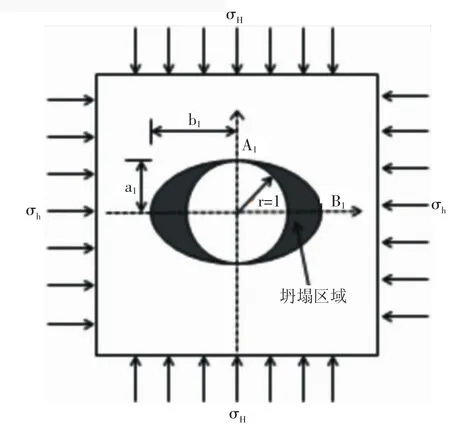
圖4 不計滲流作用(αB=0)時的井眼坍塌區域示意圖
點A和B有效周向應力和有效徑向應力達到坍塌臨界狀態時,由式(3)得:
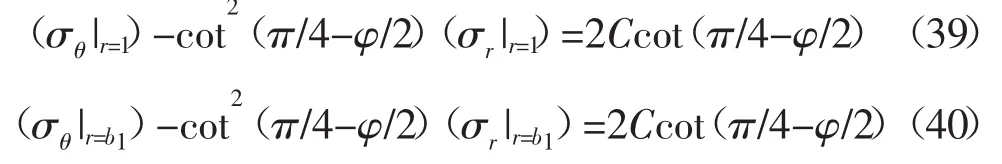
聯立式(39)和(40)可求得b1,則無因次出砂量V2為:

地應力非均勻性和考慮加速效應滲流的雙重作用時,坍塌區域邊界為一個復雜的形狀。無因次出砂量V3為:
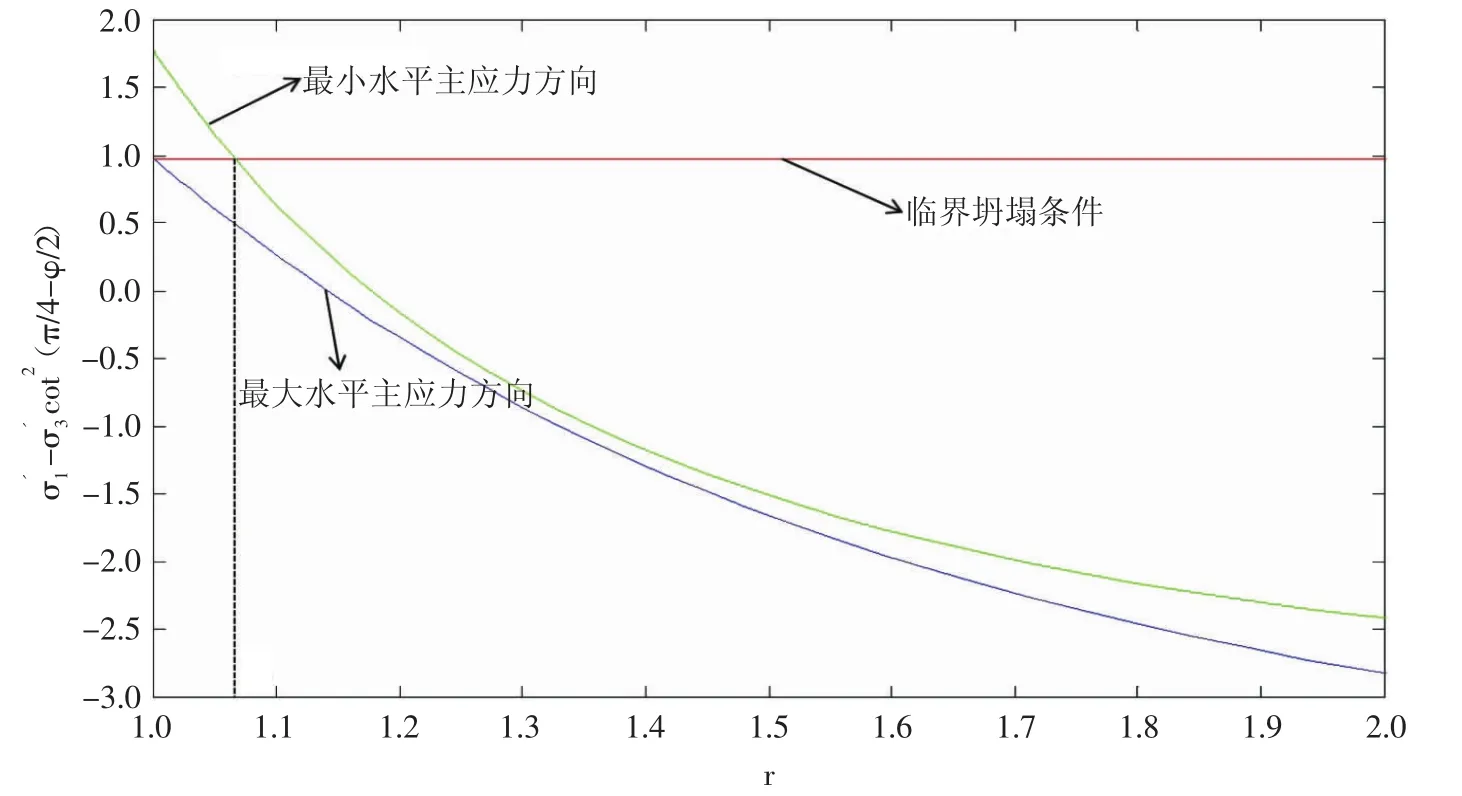
圖5 不計滲流作用時井壁圍巖達到臨界坍塌狀態時最大水平主應力方向和最小水平主應力方向的應力狀態
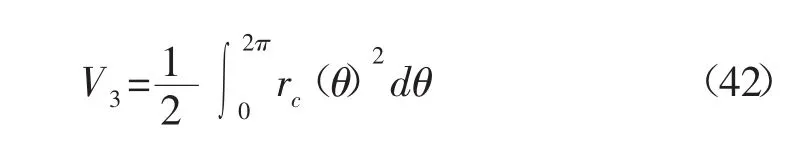
當 m=0.041,A=2.2,B=0.2,re=2 000,φ=2π/9,C=0.227 8,αB=0,λ=0.5,ξ=100 時,由地應力非均勻性和井底壓力共同作用的地層巖石應力狀態(見圖5),可以看出井壁圍巖達到臨界坍塌條件時,最小水平主應力方向對應的臨界坍塌半徑rc=1.061 7,坍塌區域(見圖6),最小水平主應力方向上坍塌半徑最大,最大水平方向沒有坍塌。由式(41)得到無因次出砂量V2為0.193 8。

圖5 不計滲流作用時井壁圍巖達到臨界坍塌狀態時最大水平主應力方向和最小水平主應力方向的應力狀態
當 m=0.041,A=2.2,B=0.2,re=2 000,φ=π/3,C=0.087 5,αB=1,η=0.5,λ=0.5,ξ=100 時,由地應力非均勻性和考慮加速效應滲流的共同作用地層巖石應力狀態(見圖7),可以看出井壁圍巖達到臨界坍塌條件時最大水平主應力方向對應的臨界坍塌半徑rc1大于最小水平主應力方向對應的臨界坍塌半徑rc2,坍塌區域(見圖8),與圖6不同此時最大水平主應力方向上存在坍塌并且最大。由式(42)得到無因次出砂量V3為4.981 4。當m=0.041,A=3.2,B=0.4,re=2 000,φ=π/6,C=0.246 2,αB=1,η=0.5,λ=0.5,ξ=100 時,坍塌區域(見圖 9),由式(42)得到無因次出砂量V3為5.326 2。可見地應力非均勻性和考慮加速效應滲流的雙重作用下的井眼坍塌區域不一定在最小水平主應力方向上坍塌最大。
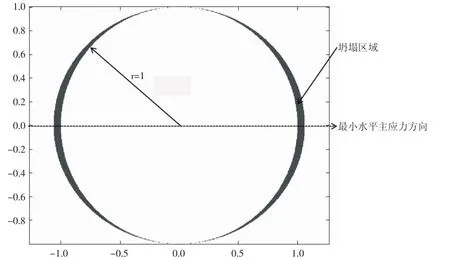
圖6 不計滲流作用時井壁達到臨界坍塌狀態時的井眼坍塌區域
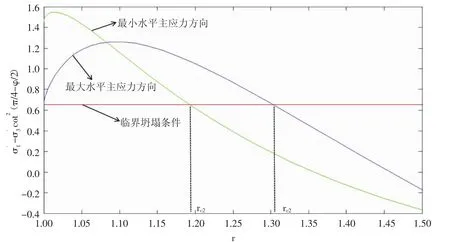
圖7 地應力非均勻性和考慮加速效應滲流的雙重作用下,最大水平主應力方向和最小水平主應力方向的應力狀態
5 結論
本文分析了油藏和氣藏在滲流作用下井壁圍巖應力狀態以及出砂量的計算,重點分析對比了氣藏在不同滲流模型下的出砂量,得到以下結論:
(1)均勻地應力場油藏徑向滲流作用下,直井有效周向應力的導數為負值并且有效周向應力的導數與有效徑向應力的導數依舊為負值;井壁坍塌最先出現在井壁,并且當井壁圍巖應力達到坍塌臨界狀態時,近井區域坍塌停止,不再發展。
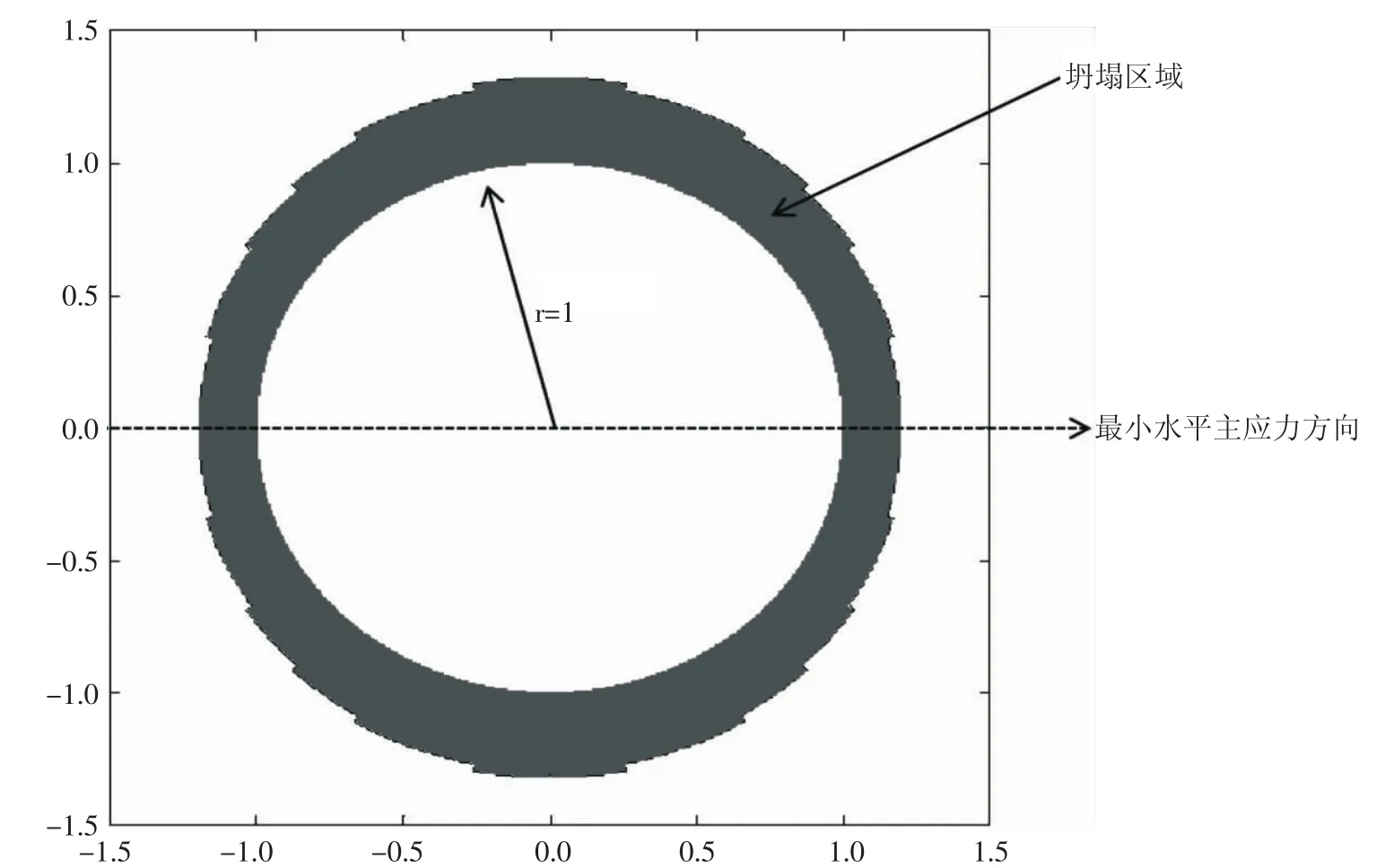
圖8 地應力非均勻性和考慮加速效應滲流的雙重作用下的井眼坍塌區域
(2)均勻地應力場氣藏徑向滲流作用下,當井壁圍巖應力達到坍塌臨界狀態時,坍塌有可能在近井區域繼續發展,而且考慮加速效應滲流模型的坍塌更易在近井區域發展,并給出了坍塌能夠在近井區域繼續發展的條件。
(3)任何θ方向上,井壁圍巖發生剪切破壞時即使考慮地應力非均勻性,考慮加速效應滲流模型所需的質量流量依然都小于Darcy滲流模型和Darcy-Forchheimer滲流模型對應的質量流量。
(4)非均勻地應力場中即使考慮滲流作用并且無論哪種滲流模型,井壁圍巖都最先在最小水平主應力方向上發生坍塌。
(5)非均勻地應力場中考慮滲流作用的近井區域可能在最大水平主應力方向上發生坍塌并且有可能最大。

