如何求解古典概型的概率

福建

吳志鵬

(作者單位：福建省泉州市德化第一中學)

如何求解古典概型的概率

福建

吳志鵬

古典概型是學生學習概率與統計的起點，是一種重要的概率模型.

一、古典概型的兩個基本特征

1.所含的基本事件個數有限;

2.每個基本事件的發生都是等可能的.

二、解決古典概型概率的基本步驟

1.分析具體問題確定樣本空間;

2.確定樣本空間包含的基本事件的總數n;

3.確定事件A所包含的不同基本事件的個數m;

三、樣本空間的選擇

1.正確選取樣本空間：要保證所選取的樣本空間所含基本事件個數是有限的，且等可能發生.

【例1】先后擲兩枚骰子，求向上點數和為奇數的概率.

【例2】射擊運動員向一靶心進行射擊．試驗的結果為：命中10環，命中9環，……，命中0環，求其命中8環以上的概率.

因為命中10環，命中9環，……,命中0環不是等可能的．因此并非古典概型，不能用古典概型的概率公式求解.

2.樣本空間的選取是相對的而非絕對的

【例3】(2016·全國卷Ⅰ文·3)為美化環境，從紅、黃、白、紫4種顏色的花中任選2種花種在一個花壇中，余下的2種花種在另一個花壇中，則紅色和紫色的花不在同一花壇的概率是

( )

【答案】C

分析：對于樣本空間的選取可分為以下兩種方案：

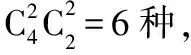
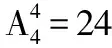
兩種方案所選取的樣本空間是不一樣的，但結果卻都是正確的，這說明基本事件總數與所研究事件包含的基本事件數必須在同一樣本空間中考慮，其結果也是相同的，因此樣本空間的選擇是相對的而非絕對的.

四、樣本點的計數

1.對于樣本空間所包含的基本事件(樣本點)總數比較少時，對樣本點的記數可采用枚舉法或樹狀圖進行表示，對于事件A所含的樣本點可從所羅列的圖表中標記獲得，直觀而具體，但應把握列舉的原則，不要出現重復和遺漏．

【例4】(2017·全國卷Ⅱ文·11)從分別寫有1,2,3,4,5的5張卡片中隨機抽取1張，放回后再隨機抽取1張，則抽得的第一張卡片上的數大于第二張卡片上的數的概率為

( )

解：法一，利用樹狀圖可以列出，從分別寫有1,2,3,4,5的5張卡片中隨機抽取1張，放回后再隨機抽取1張，所有可能結果：

2.對于樣本空間所包含的基本事件(樣本點)總數比較多時，用樹狀圖或列舉法羅列樣本點比較困難，需通過排列組合或利用加法原理與乘法原理求得.

(1)排列與組合：

②有放回的選取：從n個不同的元素中取出r個不同的元素進行排列，總數有nr種.

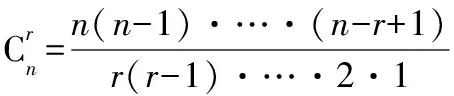
(2)兩條原理：

加法原理：做一件事，完成它可以有n類辦法，在第一類辦法中有m1種不同的方法，在第二類辦法中有m2種不同的方法，……，在第n類辦法中有mn種不同的方法，那么完成這件事共有N=m1+m2+…+mn種不同方法.每一種方法都能夠直接達成目標.

乘法原理:做一件事，完成它需要分成n個步驟，做第一步有m1種不同的方法，做第二步有m2種不同的方法，……，做第n步有mn種不同的方法，那么完成這件事共有N=m1·m2·…·mn種不同的方法.

【例5】如圖，在一個木制的棱長為3的正方體表面涂上顏色，將它的棱3等分，然后從等分點把正方體鋸開，得到27個棱長為1的小正方體，將這些小正方體充分混合后，裝入一個口袋中．

(1)從這個口袋中任意取出1個小正方體，這個小正方體的表面恰好沒有顏色的概率是多少？

(2)從這個口袋中同時任意取出2個小正方體，其中1個小正方體恰好有1個面涂有顏色，另1個小正方體至少有2個面涂有顏色的概率是多少？

分析：該模型為古典概型，基本事件個數是有限的，并且每個基本事件的發生是等可能的．題目(2)所涉及的基本事件總數比較多，所求事件中的基本事件的構成比較復雜，既要分類又要分步，融合了兩個原理及排列組合，因此學習時要注意理解原理并要掌握排列組合的方法.

【解】在27個小正方體中，恰好3個面都涂有顏色的共8個，恰好2個面涂有顏色的共12個，恰好1個面涂有顏色的共6個，表面沒涂顏色的1個．

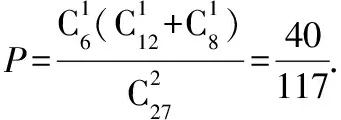
五、從古典概型具體問題中抽出的三個基本模型

1.隨機取數模型：從多個數字中任取一個，每個數字被取到的可能性相同.分為重復取得和不重復取得兩種情況.

【例6】(2016·全國卷Ⅲ文·5)小敏打開計算機時，忘記了開機密碼的前兩位，只記得第一位是M，I，N中的一個字母，第二位是1,2,3,4,5中的一個數字，則小敏輸入一次密碼能夠成功開機的概率是

( )

【答案】C

【例7】(2015·全國卷Ⅰ文·4)如果3個正整數可作為一個直角三角形三條邊的邊長，則稱這3個數為一組勾股數，從1,2,3,4,5中任取3個不同的數，則這3個數構成一組勾股數的概率為

( )

【答案】C

分析：例6可轉化為兩次分別從3個和5個不同的數字中不放回地隨機取出1個不同的數進行求解，例7則轉化為從5個不同的數字中不放回地隨機取出3個不同的數進行求解.

2.摸球問題：袋中有多種外形完全相同、顏色不同的球，現從袋中任取一球，任一球被摸到的可能性相同，分有放回和無放回的抽取兩種情況.

【例8】已知一個口袋有m個白球,n個黑球(m,n∈N*,n≥2),這些球除顏色外全部相同.現將口袋中的球隨機逐個取出，并放入如圖所示的編號為1,2,3,…,m+n抽屜內，其中第k次取出的球放入編號為k的抽屜(k=1,2,3,…,m+n).

123…m+n

試求編號為2的抽屜內放的是黑球的概率P.

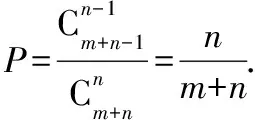
3.分信問題：n封不同的信等可能的被投到N個信箱中.

【例9】(2017·山東卷文·16改編)3名旅游愛好者計劃從3個亞洲國家A1,A2,A3和3個歐洲國家B1,B2,B3中選擇1個國家去旅游.

(1)這3名旅游愛好者有多少種旅游方案可供選擇？

(2)若3名旅游愛好者從這6個國家中任選2個去旅游,求這2個國家都是亞洲國家的概率？

分析：(1)本題可轉化為將3封不同的信投到6個不同的信箱，則有6×6×6=216種；

(作者單位：福建省泉州市德化第一中學)