“超級全能生”2018年高考全國卷26省3月聯考甲卷數學(理科)

“超級全能生”2018年高考全國卷26省3月聯考甲卷數學(理科)

一、選擇題：本題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

( )

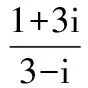
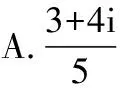
2．關于x的不等式x2-x-m<0的解集為A=(-1,n)，B={x|2x<1}，則A∩B=

( )

A．(-1,0) B．(-2,0)

C．(-∞,2) D．(0,1)

3．已知向量a=(-1,m)，b=(2,3)，若a+2b與b平行，則m=

( )

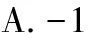
4．已知△ABC的內角A，B，C成等差數列，若AB=3，BC=4，則AC=

( )

( )

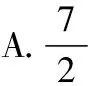
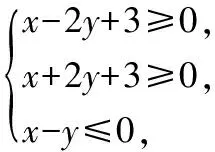
A.-6 B.-3 C.2 D.3

6．一位顧客某個月的每天都會到一家外賣店訂購午餐．該顧客一天訂購甲套餐的概率是0.8，連續兩天訂購甲套餐的概率是0.6．已知某天該顧客訂購了甲套餐，則隨后一天該顧客繼續訂購甲套餐的概率為

( )

A．0.8 B．0.75 C．0.6 D．0.48

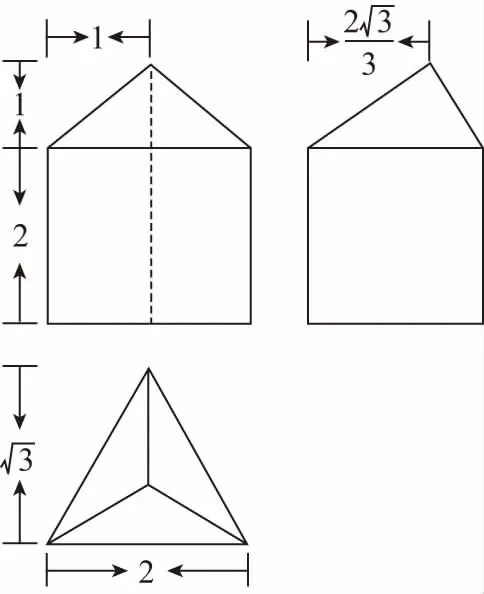
7．如圖是某幾何體的三視圖，則該幾何體的表面積是

( )

8．如圖的程序框圖的部分算法思路來源于我國古代內容極為豐富的數學名著《九章算術》中的“更相減損術”，執行該程序框圖，若輸入a,b的值分別為12，15，則輸出的m=

( )

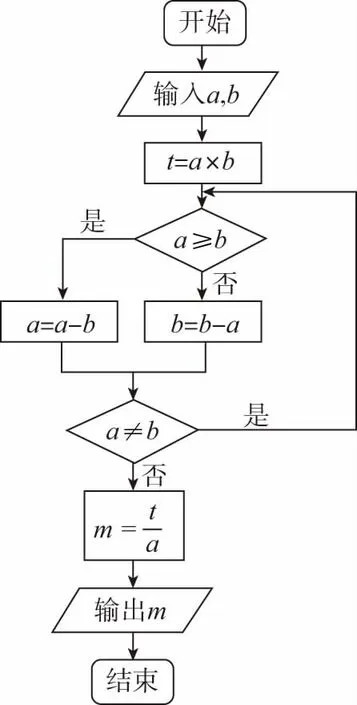
A.3 B.30 C.60 D.180

( )

( )

( )

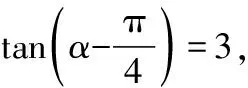
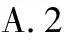
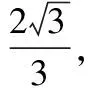
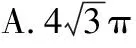
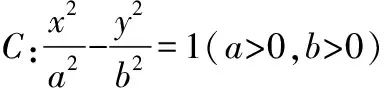
12．設函數f′(x)是f(x)(x≠2)的導函數，f(3)=0，f(2+x)+f(2-x)=0．當x>2時，f′(x)-f(x)>0，則使得f(x)·ln|x-2|<0成立的x的取值范圍是

( )

A．(-∞,1)∪(1,2) B．(1,2)∪(3,+∞)

C．(-∞,1)∪(2,3) D．(1,2)∪(2,+∞)

二、填空題：本題共4小題，每小題5分，共20分.

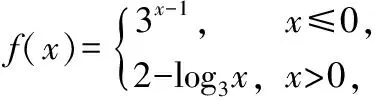
14．A，B，C，D，E五個人分別從編號為3，4，5，6，7的五張卡片中任取一張，現已知：

(1)A的數字比B的數字大2；

(2)B的數字與C的數字相鄰；

(3)C的數字是偶數；

(4)D的數字是A，B，C其中兩個數字的和．

根據以上條件B拿到的卡片上的數字為________.

15．(x+a)(x+2)4的展開式中x的偶數次冪項的系數和為-1，則實數a=________．

16．已知M，N分別是拋物線E：y2=4x和圓C：(x-4)2+y2=1上的兩個動點，當M，N運動時，|MN|的最小值為________．

三、解答題：共70分．解答應寫出文字說明、證明過程或演算步驟．第17～21題為必考題，每個試題考生都必須作答．第22,23題為選考題，考生根據要求作答.

(一)必考題:共60分.

17．(12分)

設數列{an}滿足a1+2a2+3a3+…+nan=2n-1.

(Ⅰ)求{an}的通項公式；

18．(12分)

科技扶貧是精準扶貧的一項重要措施，某科研機構將自己研發的一項葡萄種植技術提供給某山區果農．為驗證該技術的效果，該果農選擇40株葡萄樹進行試驗，其中20株不進行任何處理，記為對照組，另外20株采用新技術培養，記為實驗組．葡萄成熟收割后，該果農統計了這40株葡萄樹的年產量數據(單位：kg).

對照組1215212326243535343251524946435344616343實驗組2332343642415159464343455267656562565558

(Ⅰ)根據數據完成對照組和試驗組葡萄產量的莖葉圖，并通過莖葉圖比較對照組和實驗組葡萄產量的平均值和方差的大小(不要求計算出具體值，得出結論即可)；

(Ⅱ)若每株葡萄樹的年產量不低于45 kg，則認為“產量高”，否則認為“產量一般”．請根據此樣本完成此2×2列聯表，并據此樣本分析是否有95%的把握認為產量的提高與使用新技術有關；

對照組實驗組合計產量高產量一般合計

(Ⅲ)從“產量高”的數據中隨意抽取3株做進一步科學研究，計算恰好有2株來自實驗組的概率.

P(K2≥k)0.0500.0100.001k3.8416.63510.828

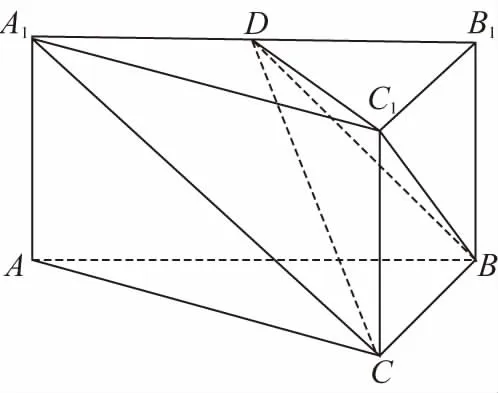
19．(12分)

(Ⅰ)求證:A1C∥平面BDC1；

(Ⅱ)求二面角B-DC1-C的余弦值.

20．(12分)

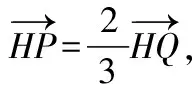
(Ⅰ)求軌跡E的方程；

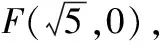
21．(12分)

已知a>0，函數f(x)=(x2-2x)lnx+ax2-x.

(Ⅰ)當a=2時，求f(x)在點(1,f(1))處的切線方程；

(Ⅱ)若函數f(x)有且僅有一個零點，求證：當x>e-2時，f(x)≥0．

(二)選考題：共10分．請考生在第22，23題中任選一題作答，如果多做，則按所做的第一題記分.

22．[選修4-4：坐標系與參數方程](10分)

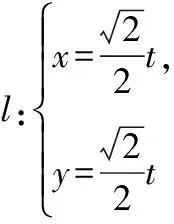
(Ⅰ)求直線l的普通方程和曲線C1的極坐標方程；

(Ⅱ)若直線l與曲線C1，C2的交點(異于極點)分別為A，B，求|AB|.

23．[選修4-5：不等式選講](10分)

(Ⅰ)當a=1時，求不等式f(x)<7的解集；

(Ⅱ)若對任意實數a，關于x的不等式f(x)+4≥|1-2m|恒成立，求實數m的取值范圍.

參考答案

17．解:(Ⅰ)當n=1時，a1=2×1-1=1；

(1分)

當n≥2時，a1+2a2+3a3+…+nan=2n-1, ①

a1+2a2+3a3+…+(n-1)an-1=2(n-1)-1, ②

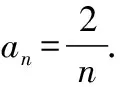
(3分)

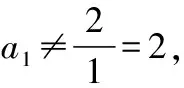
(4分)

(5分)

(6分)

(7分)

(8分)

(10分)

(11分)

(12分)

18．解:(Ⅰ)實驗組的葡萄平均產量要高于對照組的葡萄平均產量；實驗組的葡萄產量的方差要小于對照組葡萄產量的方差.

(2分)

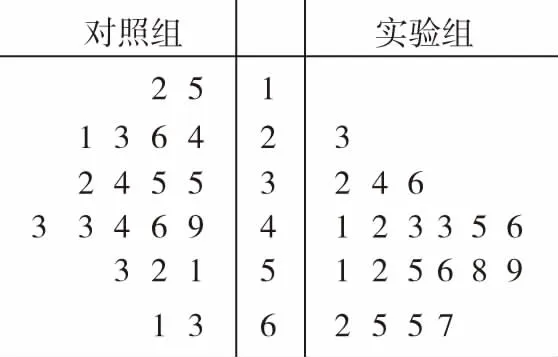
(4分)

(Ⅱ)完成2×2列聯表如下圖所示：

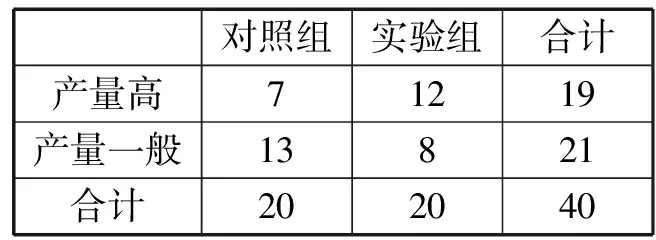
對照組實驗組合計產量高71219產量一般13821合計202040

(5分)

所以K2的觀測值

(7分)

所以沒有95%的把握認為產量的提高與使用新技術有關.

(8分)

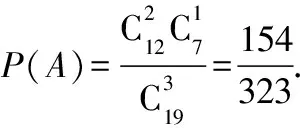
(11分)

(12分)

19．解:(Ⅰ)證明：連接B1C交BC1于E，連接DE，在直三棱柱ABC-A1B1C1中，E為BC1的中點，

又D為A1B1的中點，

所以DE是△A1B1C的中位線，所以DE∥A1C，

(3分)

又DE?平面BDC1，A1C?平面BDC1，

(4分)

所以A1C∥平面BDC1.

(5分)

(Ⅱ)因為AB2+BC2=8=AC2，所以AB⊥BC.依題意可知，AB，BC，BB1兩兩垂直，以B點為坐標原點，分別以AB，BC，BB1所在的直線為x軸、y軸、z軸，建立如圖所示空間直角坐標系B-xyz.

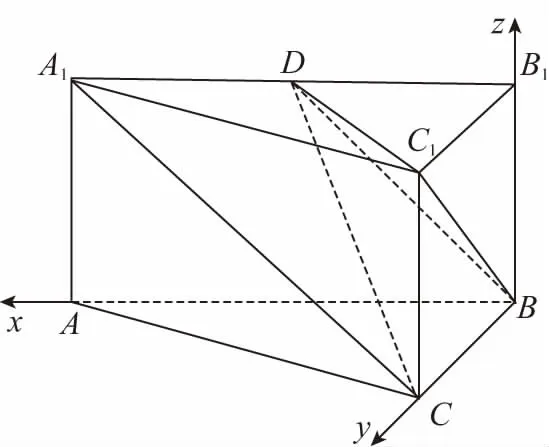
則B(0,0,0)，C(0,2,0)，C1(0,2,1)，D(1,0,1)，

(6分)

設n1=(x1,y1,z1)為平面BDC1的法向量，

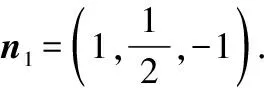
(8分)

設n2=(x2,y2,z2)為平面CDC1的法向量，

令x2=2，可得n2=(2,1,0).

(10分)

(11分)

由題知二面角B-DC1-C為銳二面角，

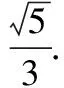
(12分)

20．解:(Ⅰ)設P(x0,y0)，H(0,y0),Q(x,y)，

(2分)

又P(x0,y0)在圓C上，

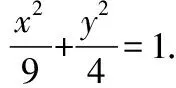
(5分)

(Ⅱ)△ABF的周長是定值，值為6.

解法一：由動點P在第一象限，可設直線AB的方程為y=kx+m(k<0,m>0)，

得(4+9k2)x2+18kmx+9m2-36=0.

(7分)

設A(x1,y1),B(x2,y2)，

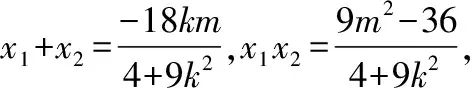
(8分)

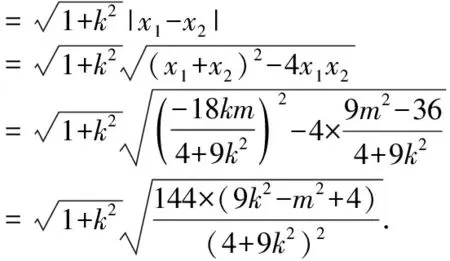
(9分)

因為直線AB與圓C:x2+y2=4相切，

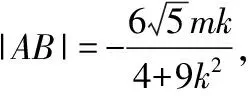
(10分)

(11分)

故△ABF的周長是定值6．

(12分)

解法二：設A(x1,y1),B(x2,y2)，

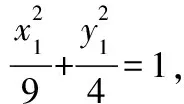
(6分)

(8分)

在圓C中，P是切點，

(9分)

(10分)

同理可得|BF|+|BP|=3，

所以|AF|+|BF|+|AB|=3+3=6，

(11分)

故△ABF的周長是定值6．

(12分)

21．解:(Ⅰ)當a=2時，f(x)=(x2-2x)lnx+2x2-x，

f′(x)=(2x-2)lnx+5x-3，

(1分)

f′(1)=2，f(1)=1，

(2分)

所以f(x)在點(1,f(1))處的切線方程為y-1=2(x-1)，即2x-y-1=0．

(4分)

(Ⅱ)證明:若函數f(x)有且僅有一個零點，

令f(x)=(x2-2x)lnx+ax2-x=0，x>0，

(5分)

(6分)

令h(x)=1-x-2lnx，

因為h′(x)<0，

所以h(x)=1-x-2lnx在(0,+)上是減函數，

又因為h(1)=0，

所以當00；當x>1時，g′(x)<0.

(7分)

所以g(x)在(0,1)上單調遞增，在(1,+)上單調遞減，

所以g(x)在x=1處取得極大值，也是最大值，g(x)max=g(1)=1.

(8分)

因為a>0，所以當函數f(x)有且僅有一個零點時，a=1．

(9分)

當a=1時，f(x)=(x2-2x)lnx+x2-x，

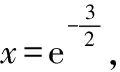
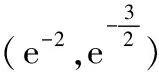
所以函數f(x)在x=1處取得極小值f(1)=0，

又因為f(e-2)=3e-2-e-4>0，所以f(x)min=f(1)=0．

(11分)

所以當x>e-2時，f(x)≥0．

(12分)

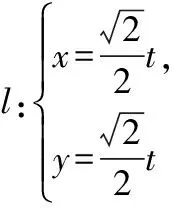
(2分)

(5分)

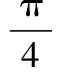
(6分)

(9分)

(10分)

23．解:(Ⅰ)當a=1時，

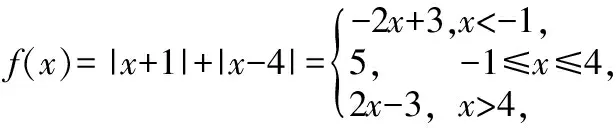
(1分)

當x<-1時，-2x+3<7，解得x>-2，所以-2

(2分)

當-1≤x≤4時，5<7恒成立；

(3分)

當x>4時，2x-3<7，解得x<5，所以4

(4分)

綜上所述，不等式f(x)<7的解集是{x|-2

(5分)

≥4(當且僅當a=±2時，取等號),

(8分)

所以4+4≥|1-2m|，所以-8≤2m-1≤8，

(10分)

(本套聯考試題為雜志社第三階段原創研發項目“數學D3T2”研發組成果)