借力思維導圖 讓學生學會有效思維策略分析
——以一道向量數量積問題的講解為例

江蘇

張 慧

(作者單位：江蘇省南京市第十三中學)

借力思維導圖 讓學生學會有效思維策略分析
——以一道向量數量積問題的講解為例

江蘇

張 慧

“導航儀”在我們的生活中起著越來越重要的作用.只要輸入起點和終點，它就可以提供不止一條的道路，我們可以從中選擇出最優的出行方案.筆者認為，“思維導圖”這一思維工具在提升學生數學思維方面與“導航儀”有著異曲同工之妙.我們在教學的過程中可以借助思維導圖，幫助學生實現數學思維策略的“從0到1”，“從1到N”，“從N到優”三個層次的進階.筆者結合平時的教學案例，談談對這一點的理解.

一、課例及其部分課堂實錄

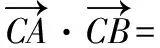
這是我校高三月考的一道填空題，班級共51名同學，其中18人做錯.試卷發下后，筆者讓學生寫了錯因分析，大致可以分為幾種：(1)條件“G是△ABC的重心”不會轉化;(2)題目中的三個條件不知道怎樣聯系起來使用;(3)想到用“基底法”求數量積，但找不到合適的基底向量;(4)想到“坐標法”求數量積，不知道怎樣建系來表示坐標.筆者借助“思維導圖”對這道題的講解分成三部分：(1)題目條件和結論的單獨聯想；(2)條件與條件、條件與結論的組合聯想；(3)幾種解題策略的優化聯想.通過這種方式來解決學生以上的困惑.

1.以單個條件、結論為“中心導航”展開聯想，為思維策略的“從0到1”做儲備.

師：當你看到“G是△ABC的重心”這一條件時你能聯想到哪些轉化？(學生在回答時教師用導圖形式呈現.)

生：

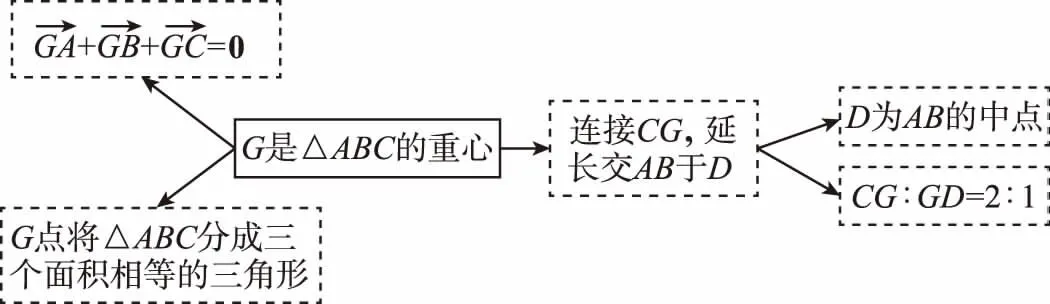
師：當看到“GA⊥GB”這一條件時同學們能聯想到哪些轉化？

生：

生：

2.以條件與條件、條件與結論為“組合導航”展開聯想，實現思維策略的“從0到1，再從1到N”.

策略一：從條件出發，將條件和條件組合聯想,嘗試得到新的結論.

組合一：

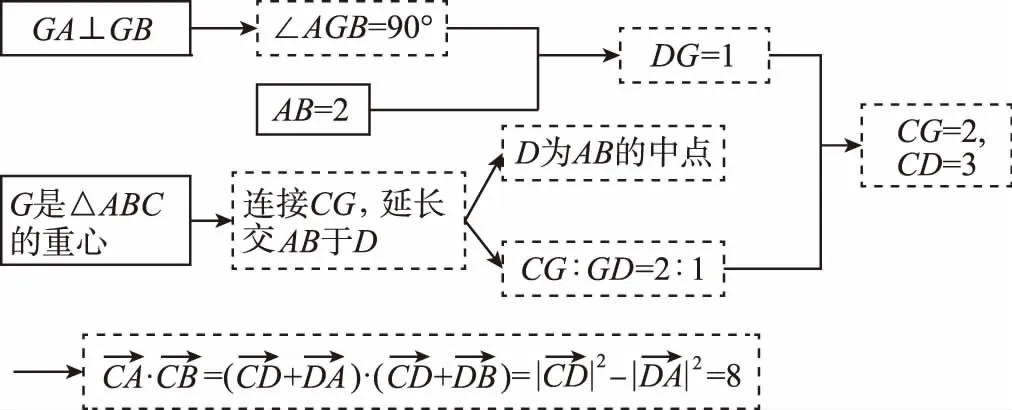
策略二：從結論出發，將條件和結論組合聯想,找到條件的轉化方向.

組合二：

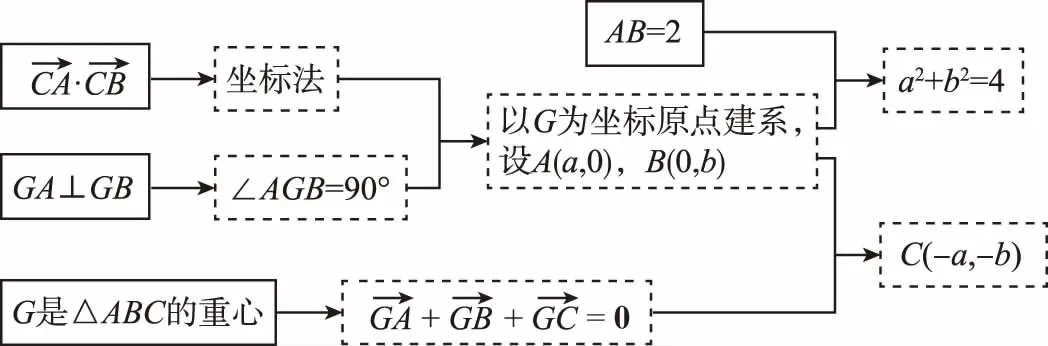
組合三：

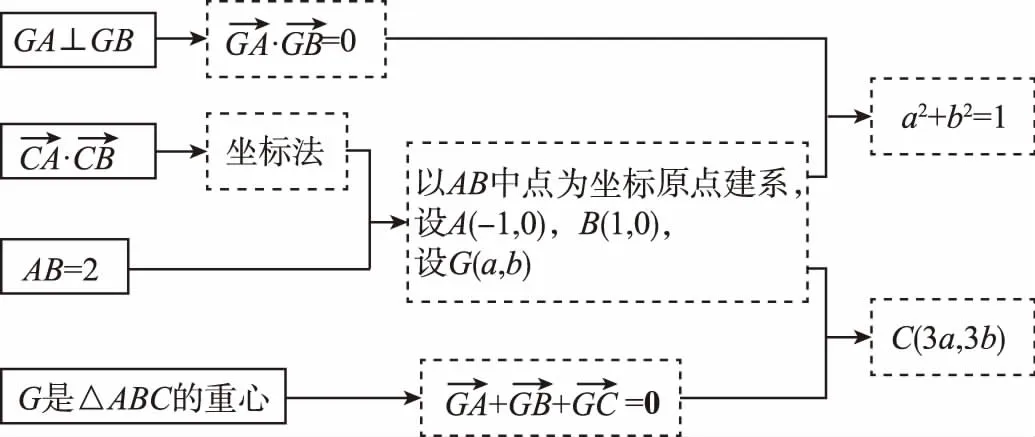
組合四：

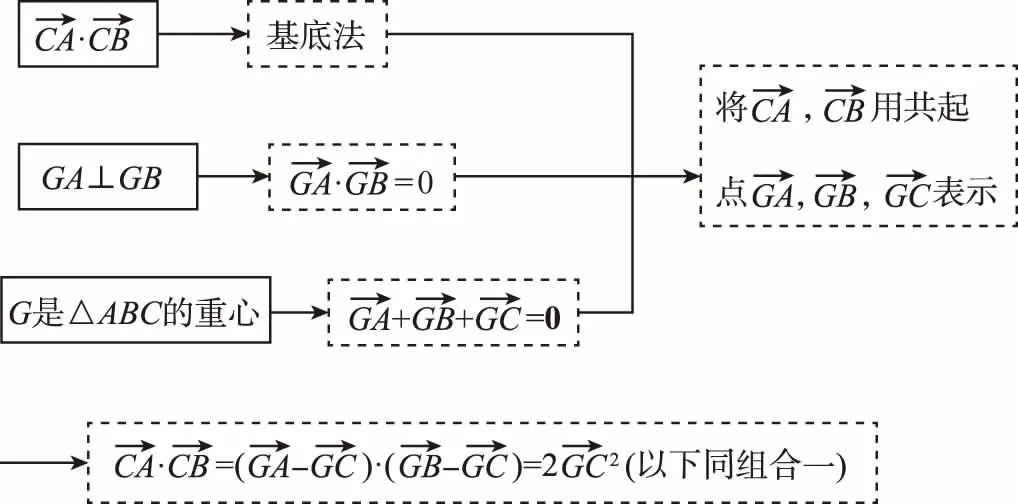
3.以各種組合整體為“比較導航”展開聯想，實現思維策略“從N到優”.

生1：對比組合一和組合四，同樣是基底法，組合一是轉化成了兩個已知長度的向量，組合四是轉化成了三個共起點的向量，運算量不一樣，顯然組合一的方法要簡單些.

生2：對比組合二和組合三兩種方案，同樣是坐標法，組合二圍繞“直角”建系更簡潔.

師：方法提煉

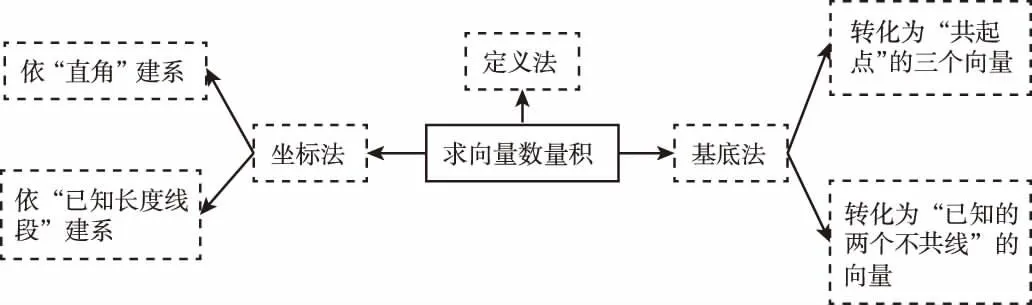
二、教學感悟

愛因斯坦曾說：“結論幾乎總是以完成的形式出現在讀者面前，讀者體會不到探索和發現的喜悅，感覺不到思想形成的生動過程，也很難達到清楚地理解全部情況.”數學老師應該將各種思路動態形成過程呈現給學生，使在解決問題中遇到困難的同學知道如何突破自己的思維障礙；使已解決問題的同學在了解幾種不同的思維角度后，優化思維策略，提升思維品質.思維導圖作為一種可視化的思考工具，將學生思維中不可言說的部分內容圖形化、示意化、可理解化，讓學生的思考從朦朧走向清晰.學生主動建構出解決問題的方法，體驗發現的喜悅，提升成就感.

1.借力思維導圖，展開知識“點”聯想，力求豐富完整，提升學生的發散思維能力.

思維導圖是一種將放射性思維具體化的方法，它的放射性結構恰好反映了大腦自然思考問題的解決過程.我們在平時教學中要注重教會學生對一些關鍵條件展開逐層聯想的方法，如：“GA⊥GB”這一條件的第一層聯想：分別在三角形、向量、解析幾何中都涉及角的研究.第二層聯想：三角形中直角讓我們聯想到直角三角形的有關性質；向量中直角讓我們聯想到數量積為0；解析幾何中直角讓我們聯想到斜率乘積為-1等.平時在對解題方法進行聯想時也要盡可能全面：比如求y=sinx+cosx+sinxcosx的最值，對求“最值”這一關鍵詞的聯想我們應想到求導、基本不等式、換元等，其中，有些方法可以解決這個問題，有些不能，所以學生有時還需要做提煉、篩選工作.這樣做雖然比較麻煩，但是可以使學生對解決一類問題的不同方法進行比較，并加深方法的記憶及掌握不同方法使用的范圍和所需條件.

2.借力思維導圖，展開組合“線”聯想，力求組合的多樣性，提升學生邏輯推理能力.

現代認知心理學認為，任何一個問題都可以分為三種狀態，即初態、終態和中間態.初態是解題的已知條件，終態是解題所要達到的終極目標.解題實質上就是使問題從初態順利地到達終態的過程.一方面我們可以通過羅列已知條件，利用對條件的逐層聯想進一步尋找各種條件的已知關聯，步步推進最終實現解題思路的導通；另一方面我們可以羅列解決這類問題的幾種一般的方法，將方法和條件進行組合聯想，明確條件的轉化方向，從而更快地推進問題求解的探索過程.通過對推理過程的合理表述可提升學生數學思維的邏輯性、流暢性.

3.借力思維導圖，逐步建構知識體系“面”，獲得“可疊加”的進步，提升思維完整性及全面性.

(作者單位：江蘇省南京市第十三中學)