基于ADAMS的高速機車雙列圓錐滾子軸承典型故障仿真分析

李長健，向立明，劉永強，廖英英

（1.石家莊鐵道大學 a.機械工程學院；b.土木工程學院，石家莊 050043；2.湖北文理學院 汽車與交通工程學院，湖北 襄陽 441053）

高速機車軸箱軸承是機車運行的重要部件，其工作狀態直接影響整個轉向架的安全運轉，進而涉及整列機車的運作。軸承出現故障時是有規律可循的，不同的故障形式和位置具有不同的故障特征，通過對軸承故障的建模和仿真探究各個部件在特定故障下的動力學行為至關重要。文獻[1]通過研究滾動軸承各部件之間的潤滑，考慮空氣阻力和油膜阻力對動力學特性的影響，引領了軸承動力學分析研究；文獻[2]建立了高速球軸承“球-溝道”及“球-保持架”的數學模型，并編制仿真軟件進行了系統仿真；文獻[3]運用流體和彈流潤滑理論建立了滾子軸承各元件的相互作用模型，并對軸承使用中遇到的各種問題進行動態模擬，但研究始終沒有涉及故障軸承。

21世紀以來，對軸承故障模型的動力學仿真研究日益增多，文獻[4]建立了深溝球軸承和角接觸軸承的動態模型，研究了軸承滾道上不同大小、不同位置凹痕缺陷對軸承內外滾道、保持架及滾子的影響；文獻[5]建立了滾子故障和麻點故障的軸承故障狀態模型，驗證了仿真與分析對研究軸承故障機理與特征提取的有效性。

上述研究對象多為部件單一，結構簡單的單列軸承，為研究雙列軸承的動力學特性，針對高速機車軸箱雙列圓錐滾子軸承建立仿真模型，探究內圈剝離故障軸承運行時某些部件的動態響應。

1 軸承幾何模型的建立

根據某型高鐵用雙列圓錐滾子軸承圖紙，運用三維建模軟件Pro/E進行正常軸承的建模。部分軸承參數見表1，在正常軸承的基礎上，將內圈剝離故障規則化處理為長度50mm，寬度1mm，深度0.3 mm的長方體凹陷，如圖1所示。同時在建模過程中做出以下基本假設[6-7]：

圖1 內圈剝離故障模型Fig.1 Model for peeling fault of inner ring

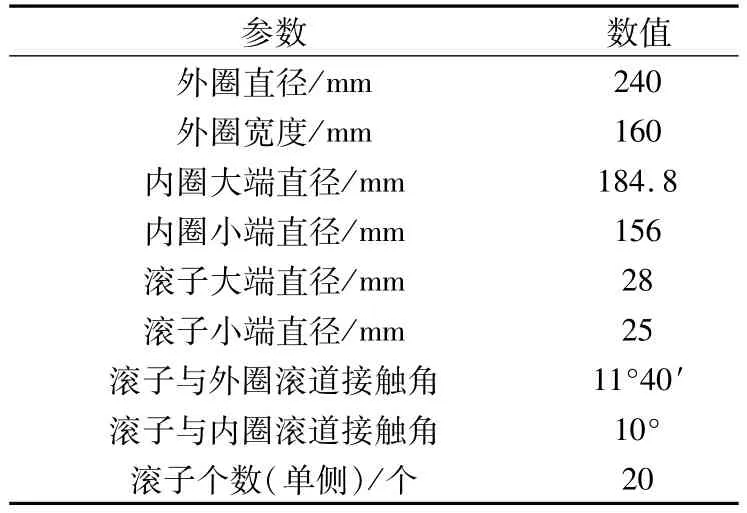
表1 軸承主要尺寸參數Tab.1 Main dimension parameters of bearing

1）雙列圓錐滾子軸承各部件在運轉過程中幾乎不經歷任何彈塑性變形；

2）模型計入軸承游隙及兜孔間隙；

3）剝離故障經規則化后初始位置位于內圈外滾道正上方。

將建立好的軸承各部件模型進行裝配，以隔圈質心位置為基礎坐標系，進行內、外圈的裝配，滾子按角度陣列裝配，最后進行保持架的裝配。裝配完畢后進行干涉檢查，保證各部件之間無干涉[8]。模型如圖2所示。

圖2 軸承裝配示意圖Fig.2 Assembly diagram of bearing

2 動力學模型的建立

軸承內圈、外圈、滾子及保持架所用材料及其屬性[9]見表2。

表2 軸承各部件材料屬性Tab.2 Material properties of bearing components

2.1 接觸關系

雙列圓錐滾子軸承各部件接觸繁多，按接觸部件可分為內圈與滾子、外圈與滾子、保持架與滾子、內圈與隔圈、內圈與保持架（內圈引導）、外圈與保持架（外圈引導）等，所需設置的接觸個數總共為126個。其中內圈與隔圈、內圈與保持架、外圈與保持架的接觸逐個添加，而滾子與內圈、外圈、保持架的接觸由于個數較多，采用ADAMS中的宏命令方法進行添加[10]。

ADAMS環境下的接觸方式有補償法和沖擊脈沖法，從參數更便于確定的角度，本模型采用沖擊脈沖法。為得到精確的結果，需要準確選擇剛度系數、阻尼系數、碰撞系數、切入深度等參數：

1）對于旋轉物體的碰撞，其剛度系數k和阻尼系數可近似用以下方法[11]進行確定，

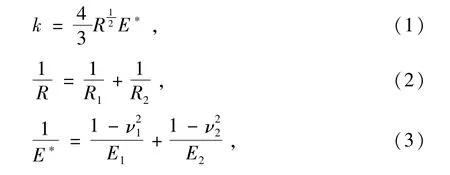
式中：R1，R2分別為兩碰撞物體的接觸半徑，mm；ν1，ν2分別為兩接觸物體的泊松比；E1，E2分別為兩接觸物體的彈性模量；阻尼系數數值通常設置為剛度系數數值的0.1%～1%。

2）切入深度表示當兩接觸物體碰撞阻尼達到最大值時的互相侵入深度，為達到仿真環境要求且節約仿真時間，切入深度設置為0.1 mm。

3）碰撞系數反應了接觸材料的非線性程度，在ADAMS中金屬與金屬之間的碰撞系數值通常設置為1.5。

4）在ADAMS中，接觸物體間摩擦力的定義采用庫侖法。在考慮潤滑時，鋼與鋼之間的靜態摩擦因數為0.10～0.12，動態摩擦因數為0.05～0.10[6]：19；鋼與尼龍之間的靜態摩擦因數為 0.37，動態摩擦因數為0.34。考慮到接觸表面的表面粗糙度和油膜厚度的影響并經過大量仿真試驗，將滾子與內、外圈之間的靜態摩擦因數和動態摩擦因數分別定義為0.12，0.10；滾子與保持架之間的靜態摩擦因數和動態摩擦因數分別定義為0.37，0.34。

2.2 約束、載荷、激勵的添加

為模擬軸承外圈固定、內圈旋轉的實際工況，將兩內圈、隔圈與絕對坐標系間設置為旋轉副，為保證軸承運動時外圈的旋轉不影響其振動，在外圈與絕對坐標系之間設置扭簧[12]，扭簧的剛度系數和阻尼系數分別為1×1010N·mm/deg，1×108N·mm·s/deg。

為模擬高速機車軸承高速輕載的工作環境，重力方向豎直向下；外圈施加40 kN的徑向載荷，其大小固定不變；內圈與隔圈的轉速為1 500 r/min。

3 模型驗證

3.1 滾動軸承的時域運動學特性

軸承內、外圈轉速一定時，保持架和滾子的轉速分別為[13]

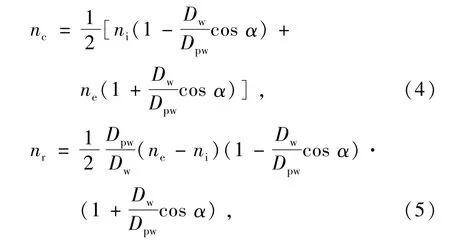
式中：nc為保持架轉速，r/min；nr為滾子轉速，r/min；ni為內圈轉速，r/min；ne為外圈轉速，r/min；Dw為滾子直徑，mm；Dpw為滾子組節圓直徑，mm；α為接觸角。

設定軸承內圈轉速ni＝1 500 r/min，計算可得 nc＝646.6 r/min，即3 879.6 deg/s；nr＝4 629.8 r/min，即27 778.8 deg/s。徑向載荷40 kN時，在ADAMS環境下仿真得到的保持架及滾子轉速與理論值的對比如圖3所示。

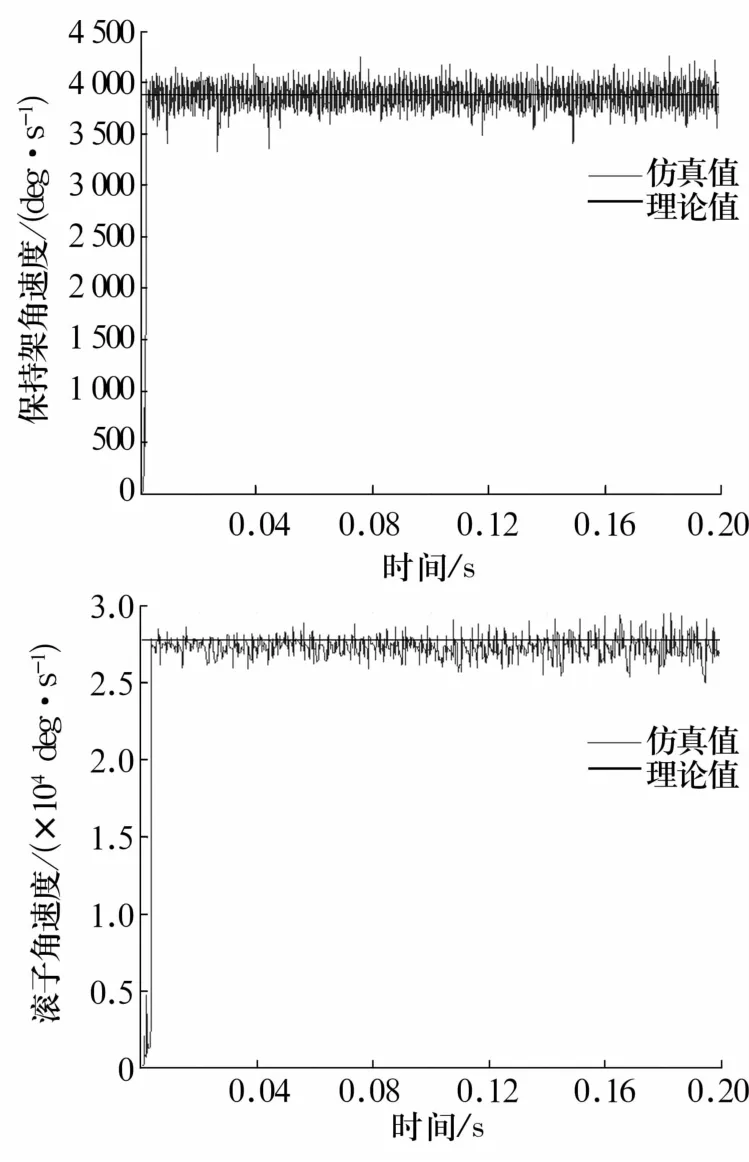
圖3 保持架及滾子轉速仿真結果Fig.3 Simulation results of rotational speed of cage and roller

從圖3可以看出：保持架轉速約650 r/min，與理論計算值誤差為0.53%；滾子轉速約4 583 r/min，與理論計算值誤差為1%。考慮到理論值計算誤差以及模型的建立、仿真誤差，上述誤差值處于合理范圍，也驗證了模型在運動學方面的合理性。

3.2 內圈故障驗證

內圈故障特征頻率理論值為[14]

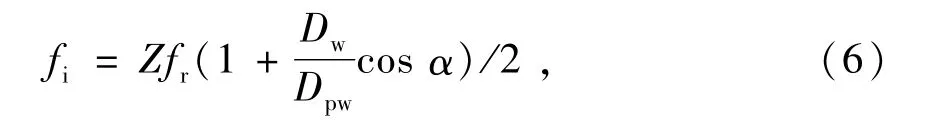
式中：fi為內圈故障特征頻率；fr為內圈轉動頻率；Z為滾子個數。內圈轉速1 500 r/min，徑向載荷40 kN時，計算得內圈故障特征頻率為284.4 Hz。

運用共振解調方法對仿真得到的加速度信號進行分析，提取故障特征，處理后結果如圖4所示。從圖中可以看出，故障特征頻率1倍及2倍頻明顯，但邊頻帶不明顯。內圈故障邊頻帶的產生是由于滾動軸承在外載荷下，在承載區內時，內圈故障隨內圈轉動與滾子接觸產生的沖擊脈沖幅值比故障在非承載區內產生的沖擊脈沖幅值大，從而形成了對故障特征頻率的調制，調制頻率為內圈轉頻[15-16]；而本次在ADAMS環境下的仿真模型采用的是全剛體，施加的載荷對外圈影響較小，承載區與非承載區差別不大，且徑向載荷的施加比較集中，所以造成圖中邊頻帶不明顯。但故障特征頻率1倍和2倍頻較明顯，可以較好地驗證故障模型的有效性。

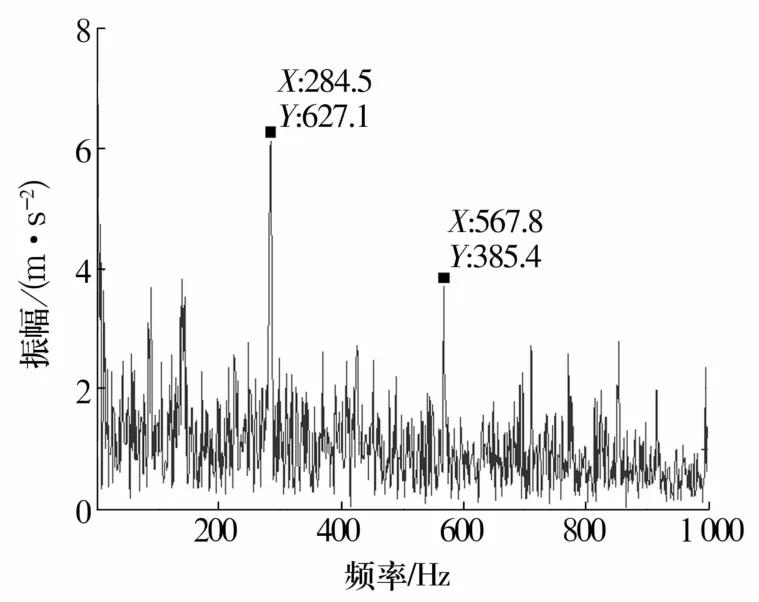
圖4 內圈剝離故障振動信號的頻域Fig.4 Domain frequency of vibration signal for peeling fauly of inner ring

4 仿真分析

模擬雙列圓錐滾子軸承單側內圈剝離故障，進行仿真分析，以了解故障側和非故障側的不同行為。

4.1 滾子的轉速突變

選取在兩側內圈同一位置的2個滾子，如圖5所示。觀察故障側和非故障側滾子轉速的變化特征，結果如圖6所示。從圖中可以看出：非故障側滾子運行平穩；故障側滾子在運行過程中的轉速發生了3次突變，突變間隔約0.07 s，與理論計算所得滾子每次與故障接觸時間間隔相同。綜上，可以斷定故障與圖5中選取的故障側滾子恰好接觸了3次，可見滾子在與故障接觸時受到了較大沖擊，轉速急劇下降，產生打滑現象。而內圈在0.2 s時間內的轉數為5圈，與滾子與故障接觸次數不同的原因是故障隨內圈轉動，且內圈與滾子公轉有速度差。

圖5 滾子選取示意圖Fig.5 Selection diagram of roller

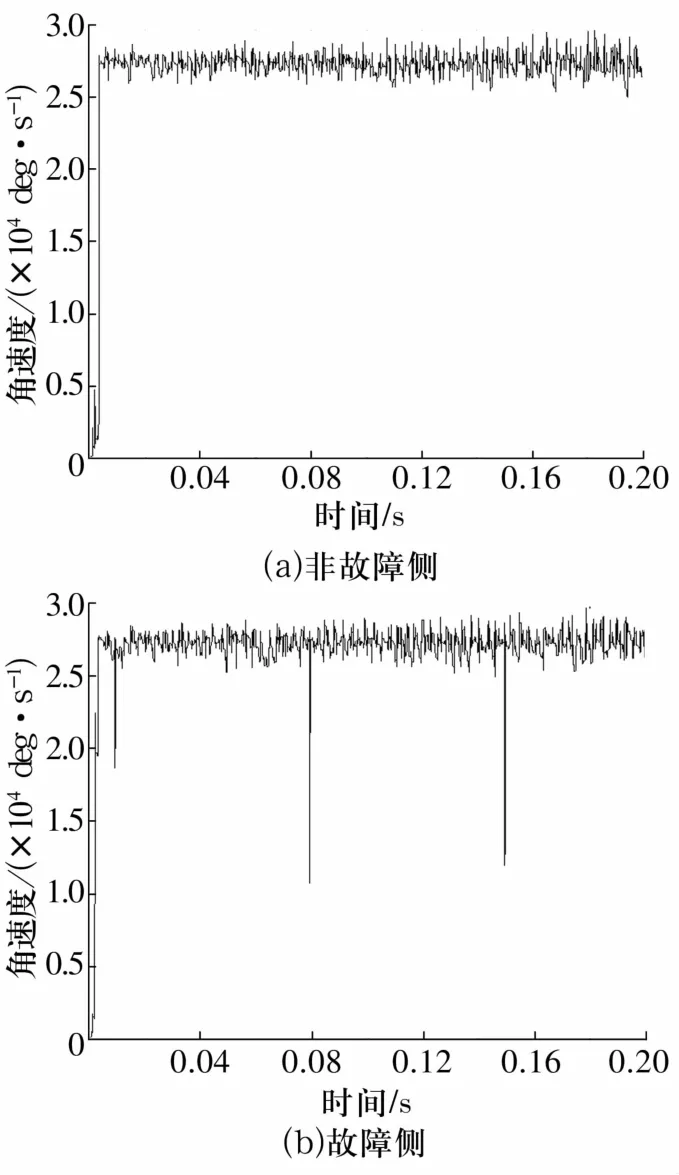
圖6 滾子轉速曲線圖Fig.6 Curve graph of rotational speed of roller

4.2 保持架質心的運動軌跡

觀察運行過程中兩側保持架質心位置的變化并進行對比，結果如圖7所示。從圖中可以看出：非故障側保持架質心的橫向運動范圍為-1.26～0.71 mm，縱向運動范圍為-1.39～1.02 mm，整體運行比較規律，由起始位置緩慢向外旋轉延伸，保持架穩定性較好；而故障側保持架質心的橫向運動范圍為-0.62～0.70 mm，縱向運動范圍為-0.61～0.60 mm，與非故障側相比運動由起始位置快速向外延伸，在個別區域表現的雜亂無章，保持架穩定性較差。

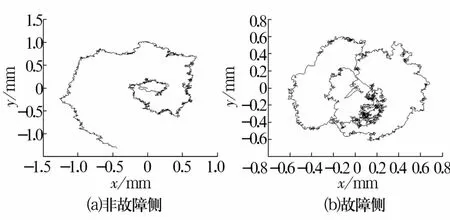
圖7 保持架質心位置變化軌跡Fig.7 Change trajectory of mass center position of cages

5 結論

建立了高速機車軸箱處雙列圓錐滾子軸承內圈剝離故障模型，經過對模型各部件轉速、故障特征頻率與理論值的對比，驗證了模型的有效性。對模型進行動力學仿真分析得到如下結論：

1）雙列圓錐滾子軸承在運行時，內圈轉動的同時滾子也在進行公轉，滾子公轉轉速即保持架轉速。由于內圈與保持架存在速度差，且內圈故障隨內圈轉動，因此每個滾子與故障接觸次數與內圈轉數并不相同，且滾子每次與故障接觸都使滾子轉速急劇下降，產生打滑。

2）雙列圓錐滾子軸承在運行時，內圈故障在導致滾子運動異常時，也將沖擊影響傳遞給了相應的保持架，致使保持架在整個運動區域內運動不規律，穩定性大大降低，從而影響整個軸承的正常運轉。