滾輪軸承最大允許動載荷的計算
劉建志,郭衛東
(常州東風軸承有限公司,江蘇 常州 213022)
通過滾輪軸承最大允許動載荷可判斷滾輪軸承主參數設計是否合理,若滾輪軸承最大允許動載荷小于滾輪軸承的當量動載荷,則滾輪軸承外圈將會發生彎曲斷裂。為設計合理的滾輪軸承主參數,提高滾輪軸承的可靠性,需探討滾輪軸承最大允許動載荷的計算方法。
1 滾輪軸承主參數的設計
以NUTR類滾子滾輪軸承為例,不帶密封圈的滿裝滾子滾輪軸承主參數為
Dw=KDw(D-d),
(1)
Dpw=KDpw(D+d),
(2)
Le=KLeC,
(3)
De=Dpw+Dw,
(4)
D2=De-KD2Dw,
(5)
(6)
(7)
在設計的初始階段也可取
φ=360°/Z,
(8)
式中:Dw為滾子直徑;Dpw為滾子組節圓直徑;D為軸承外徑;d為軸承內徑;KDw為滾子直徑系數;KDpw為滾子組節圓直徑系數;Le為外圈滾道寬度;KLe為滾道寬度系數;C為外圈寬度;De為外圈滾道直徑;D2為外圈擋邊直徑;KD2為外圈擋邊直徑系數;Z為滾子數量;δc為相鄰兩滾子間的周向游隙;φ為相鄰兩滾子的夾角。
在已知d,D及C的條件下,根據經驗可進行主參數的設計,這里不作詳細探討。
2 滾輪軸承外圈截面參數
NUTR類滾子滾輪軸承外圈截面為槽形(圖1),為簡化截面參數計算,內邊緣直徑近似取滾道直徑和擋邊內徑的平均值,外邊緣直徑取外圈外徑,雖對計算精度有影響,但能滿足工程應用需要。外圈截面面積為

圖1 外圈截面示意圖
(9)
外圈中性圓半徑為
(10)
外圈形心圓半徑為
(11)
外邊緣應力系數為
(12)
內邊緣應力系數為
(13)
3 滾輪軸承受力分析
3.1 滾子載荷分析
滾輪軸承受載過程中,經歷半圈滾子受載到少于半圈滾子受載,但在初始瞬間滾子載荷分布符合Weibull分布,如圖2所示。根據文獻[1]可知在β=0位置滾子受載最大,最大載荷為
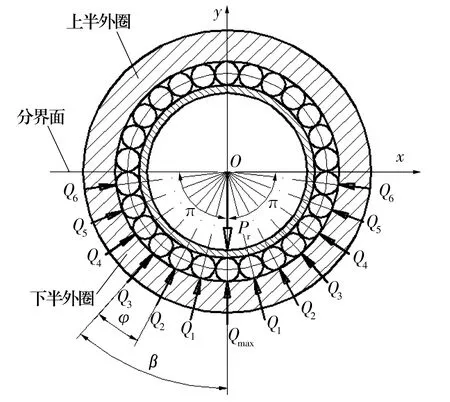
圖2 滾子受載示意圖
Qmax=4.08Pr/Z,
(14)
式中:Pr為滾輪軸承的當量動載荷。
第i個滾子所受載荷為
Qi=Qmaxcos1.1(iφ);i=1,2,…,n,
(15)
n=(Z-2)/4。
3.2 外圈受力分析
3.2.1 下半外圈
假想將滾輪軸承的外圈從圖2中的x軸線切開后,下半外圈相當于一個中間單支點的簡支半圓形梁,其受力狀態如圖3所示。載荷通過滾子的傳遞作用在下半外圈上,使下半外圈發生由內向外的法向彎曲變形,而上半外圈有限制下半外圈發生彎曲變形的內力,內力用分界面上的法向拉力和切向剪力表示,上半外圈對下半外圈的法向拉力N垂直于分界面,作用在中性圓上;上半外圈對下半外圈的切向剪力V平行于分界面,同樣作用在中性圓上。

圖3 下半外圈受力圖
由靜力學平衡方程組∑Fx=0和∑Fy=0得
(16)
(17)
Frmax=Qmax,
Fri=Qi,
式中:Frmax為β=0位置滾子對外滾道的法向力;Fri為第i個滾子對外滾道的法向力。
由(16)和(17)式得
(18)
(19)
將(15)式代入(18),(19)式得
N=QmaxKQN,
(20)
V=QmaxKQV,
(21)
3.2.2 上半外圈
上半外圈無外力作用,只存在下半外圈對上半外圈的法向拉力N和切向剪力V,力的方向和作用位置如圖4所示。

圖4 上半外圈受力圖
上半外圈任意截面的受力如圖5所示,Nθ為任意截面上的法向拉力,Mθ為任意截面上的彎矩。根據力和力矩的平衡關系可得

圖5 任意截面受力圖
Nθ=Ncosθ+Vsinθ,
(22)
Mθ=Rz[N(1-cosθ)-Vsinθ]。
(23)
4 外圈的邊緣應力
根據文獻[2]74-77可得上半外圈任意截面外、內邊緣應力分別為
(24)
(25)
分別將(22),(23)式代入(24),(25)式得
σw={Rz[N(1-cosθ)-Vsinθ]Kw-
(Ncosθ+Vsinθ)}/Ah,
(26)
σn=-{Rz[N(1-cosθ)-Vsinθ]Kn+
(Ncosθ+Vsinθ)}/Ah。
(27)
當θ=0時
(28)
(29)
當θ=90°時,在對稱軸線的橫截面上有2個彎矩M90,則
(30)
(31)
作用在90°截面上的法向拉力是按V或2V計算還存在不同看法,因V對邊緣應力的計算影響較小,故(30),(31)式中暫取V。
通過(28)~(31)式可知:θ=90°截面上外、內邊緣的應力值大于θ=0°截面上外、內邊緣的應力值。
為了分析在(0,90°)區間的最大邊緣應力與σw90,σn90的關系,對(26),(27)式求導得
(32)

(33)
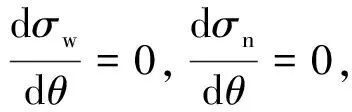
(34)
(35)
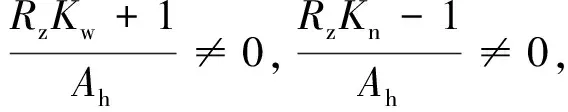
Nsinθ-Vcosθ=0,
(36)
可得
(37)

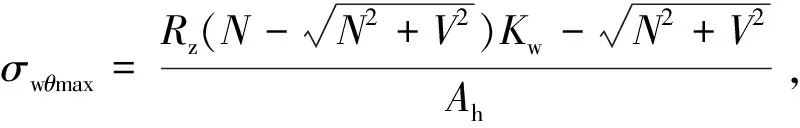
(38)
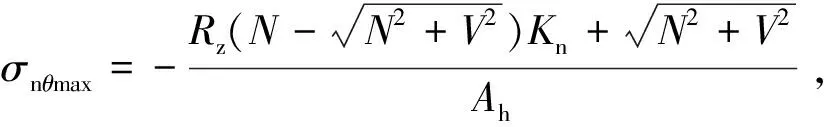
(39)
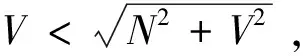
σwθmax<σw90,
(40)
σnθmax<σn90,
(41)
故在[0,90°]區間最大邊緣應力發生在θ=90°位置截面上。
下半圈y軸所在截面的彎矩是分界面上的內力對y軸所在截面的彎矩與各法向載荷Fri對y軸所在截面的彎矩差,故作用在下半圈y軸所在截面的彎矩小于上半圈y軸所在截面的彎矩,由此判斷最大邊緣應力在上半外圈上。
5 最大邊緣應力的實例計算
NUTR50和NUTR50110滾輪軸承主參數見表1,分別根據國外某公司樣本中的最大允許動載荷Prmax、最大允許靜載荷P0rmax、有效額定動載荷Crw、有效額定靜載荷C0rw計算最大邊緣應力,結果見表2和表3。

表1 NUTR50和NUTR50110的主參數
由表2、表3可知:當用Crw,C0rw,P0rmax計算外圈的最大邊緣應力時,外、內邊緣應力無規律性;當用最大允許動載荷計算外圈的最大邊緣應力時,NUTR50和NUTR50110外圈的最大外邊緣應力σw90很接近,最大內邊緣應力σn90也比較接近;用最大允許動載荷計算的最大邊緣應力有一定的規律性。由此可推斷:滾輪軸承的最大允許動載荷受外圈最大允許邊緣應力約束,最大允許動載荷根據最大允許邊緣應力計算得到。

表2 NUTR50外圈最大邊緣應力

表3 NUTR50110外圈最大邊緣應力
6 滾輪軸承最大允許動載荷
將(20),(21)式代入(30)式得
(42)
由(42)式得到用外邊緣應力表示的滾子最大載荷為
(43)
將(22),(23)式代入(33)式得
(44)
取σn90的絕對值,由(44)式得到用內邊緣應力表示的滾子最大載荷為
(45)
由(14)式得
Pr=QmaxZ/4.08,
(46)
將(43),(45)式分別代入(46)式得到用外、內邊緣應力表示的當量動載荷分別為
(47)
(48)
最大邊緣應力應滿足強度條件,即
(49)
(50)
式中:σtp為材料熱處理后的許用抗拉應力;σcp為材料熱處理后的許用抗壓應力;σb為材料熱處理后的抗拉強度;σbc為材料熱處理后的抗壓強度;Sw為外邊緣應力安全系數;Sn為內邊緣應力安全系數。
將(49)式代入(47)式得
(51)
將(50)式代入(48)式得
(52)
由于內邊緣直徑近似取滾道直徑和擋邊內徑的平均值,而外邊緣直徑取外圈外徑,外邊緣應力比內邊緣應力計算準確度高。若已知許用抗拉強度和許用抗壓強度,用(51),(52)式右式的前項計算;若已知材料抗拉強度、抗壓強度極限及外、內邊緣應力安全系數,則用(51),(52)式右式的后項計算。
邊緣應力安全系數可通過以下方法得到:1)根據國外著名軸承公司滾輪軸承樣本中的最大允許動載荷及滾輪軸承樣品的測量主參數用第3節方法反推;2)根據國外主機制造公司滾輪軸承訂貨圖中的最大允許動載荷和主參數用第3節方法反推;3)根據滾輪軸承應用條件參考文獻[2]104-107的推薦值選擇;4)通過試驗取得。當數據積累到一定程度后就可以形成各類滾輪軸承(包括其他外圓非包容軸承)在不同應用條件下的邊緣應力安全系數。
根據文獻[3],對于淬硬的GCr15鋼制外圈,σb約2 100 MPa,σbc約3 700 MPa,推算NUTR50和NUTR50110邊緣應力安全系數的平均值為Sw=2.67,Sn=3.36。
7 結束語
通過對滾輪軸承外圈的受力分析及強度理論得到滾輪軸承外圈最大邊緣應力,并通過實例分析得到:滾輪軸承的最大允許動載荷根據最大允許邊緣應力計算得到。通過將最大允許動載荷與當量動載荷對比可驗證主參數設計的合理性,并對主參數進行修正。但滾輪軸承的主參數設計不僅與最大允許動載荷有關,還與最大允許靜載荷、有效額定動載荷、有效額定靜載荷有關,如何計算這些載荷參數及處理主參數設計與各個載荷參數之間的關系,有待后續做進一步的研究。
文中以常見的NUTR50和NUTR50110滾輪軸承滾輪軸承為例分析,其他結構形式的向心滾輪軸承,如深溝球滾輪軸承、角接觸球滾輪軸承、圓錐滾子滾輪軸承,也可參照本文的研究方法進行計算。

