灰色預測模型的改進及其在電力行業(yè)中的應用

許昌學院 信息工程學院,河南 許昌 461000)

隨著當今社會生產力的日益發(fā)達和科學技術的快速發(fā)展，預測分析學在各種領域得到了迅速的發(fā)展和應用，根據(jù)預測分析的結果從而減少對未來事物認識的不確定性，以指導決策行動和長遠規(guī)劃，減少決策和規(guī)劃的盲目性，在工程應用領域中具有十分重要的意義[1,2].復雜系統(tǒng)的事件預測分析是指根據(jù)復雜系統(tǒng)已知的客觀信息運用各種定性和定量的分析理論與方法，對復雜系統(tǒng)的內部或者復雜系統(tǒng)的外部存在的某些設計特征或者發(fā)展狀態(tài)進行的一種估計、測算和分析的過程活動[3].目前，在復雜系統(tǒng)預測分析的過程中，常用的預測分析方法有定性分析法，數(shù)學模型法如時序模型法、回歸模型法、動態(tài)需求系統(tǒng)等以及模擬仿真方法等，這些方法分別具有相應的應用領域和面向對象，具有一定的應用效果[4-6].灰色系統(tǒng)理論是由鄧聚龍教授首先提出并創(chuàng)立的一門新興學科，它基于數(shù)學理論去解決一些包含未知因素的特殊領域的問題，特別適合于解決“外延明確，內涵不明確”的“小樣本，貧信息”問題[7-10].復雜系統(tǒng)的事件預測往往包含有灰色信息，因此，為了解決這種問題實現(xiàn)對復雜系統(tǒng)灰色事件的預測，本文將在灰色系統(tǒng)理論的基礎上，給出一種基于改進的灰色聚類分析方法的預測模型，并通過其在電力負荷預測中的應用進行驗證和分析，以說明模型的有效性.

1 灰色序列與灰色關聯(lián)系數(shù)

灰色系統(tǒng)理論提出了對復雜系統(tǒng)不同層級的分系統(tǒng)進行灰色關聯(lián)分析的概念，對復雜系統(tǒng)發(fā)展變化態(tài)勢、因素關聯(lián)以及狀態(tài)動態(tài)變化關系等提供了量化的度量，這里包括灰色序列和灰色關聯(lián)系數(shù)兩個重要的概念.

1.1 灰色序列的生成

復雜系統(tǒng)的狀態(tài)變化具有時序性，將影響復雜系統(tǒng)行為的n個相關因素組成的數(shù)據(jù)序列，稱比較數(shù)列Vi，則m種時序狀態(tài)對應的比較數(shù)列分別為

V1={v1(1),v1(2),…,v1(n)}，
V2={v2(1),v2(2),…,v2(n)}，
……
Vm={vm(1),vm(2),…,vm(n)}.

(1)

特別地，將反映復雜系統(tǒng)行為和狀態(tài)特征的數(shù)據(jù)序列，稱為參考數(shù)列V0，即：

V0={v0(1),v0(2),…,v0(n)}.

(2)

1.2 灰色關聯(lián)系數(shù)

為了能夠表征不同時序下系統(tǒng)發(fā)展狀態(tài)的關聯(lián)性，灰色系統(tǒng)理論給出了描述隨時間或不同對象而變化的關聯(lián)性大小的量度，灰色關聯(lián)系數(shù)ξi和灰色關聯(lián)度ri.

灰色關聯(lián)系數(shù)ξij表示比較數(shù)列Vi與參考數(shù)列V0關于不同影響因素之間的關聯(lián)性，即：

(3)

其中，β為分辨系數(shù)，β∈[0,1]，一般取β=0.5.Δ(vi(j)-v0(j))表示量值差值.

灰色關聯(lián)度ri表示比較數(shù)列Vi與參考數(shù)列V0的整體曲線的接近程度，即:

(4)

2 基于改進的灰色聚類分析的預測模型

2.1 灰色經典域與灰色節(jié)域

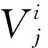
(5)

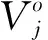
(6)

2.2 預測特征的權重

復雜系統(tǒng)的影響因素有多種，不同的預測特征一般具有不同的重要度即權重，為此需要對灰色聚類分析的特征進行權重分配.本文采用綜合評價法對預測特征權重進行分配，首先請位領域專家采用1-9的比率標度對不同預測特征重要度進行打分，獲得初始評判分析矩陣B.

(7)

則預測特征j的權重wj為

(8)

2.3 預測特征的處理

不同的預測特征一般具有不同的量綱，為了能夠有效地進行預測分析，需要將所有預測特征經典域無量綱化，使其具有統(tǒng)一的量值標度.

(9)

(10)

2.4 灰色關聯(lián)系數(shù)與灰色關聯(lián)度

假設獲得待測系統(tǒng)的樣本數(shù)據(jù)序列Vd為，即：

Vd={vd(1),vd(2),…,vd(n)}.

(11)

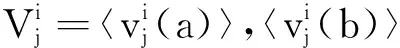
(12)

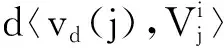
(13)

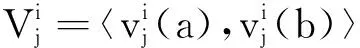
(14)

(15)

2.5 模型與算法實現(xiàn)

根據(jù)上述論述可知，在灰色聚類分析的基礎上，通過對比同類的預測特征進行灰色經典域和灰色節(jié)域的構建，獲得待預測系統(tǒng)與不同類別之間的灰色關聯(lián)系數(shù)和灰色關聯(lián)度，根據(jù)綜合灰色關聯(lián)度的數(shù)值確定待測系統(tǒng)歸屬于哪一類狀態(tài)集，從而獲得基于灰色聚類分析的預測結果.

具體而言，基于改進的灰色聚類分析的預測模型實現(xiàn)過程如下.

步驟1,基于預測分析系統(tǒng)的相關影響因素，獲得對應的時序分析數(shù)列.

步驟2,基于預測分析系統(tǒng)的預測特征，將待測系統(tǒng)進行歸屬類別劃分，形成不同預測特征的狀態(tài)集即類別集合.

步驟3,構建不同類別集合關于不同預測特征的灰色經典域和灰色節(jié)域.

步驟4,對不同類型和量綱的預測特征進行統(tǒng)一標度處理，并獲得對應特征的權重.

步驟5,獲取待測系統(tǒng)的相關影響因素的數(shù)據(jù)，并獲得其關于不同影響因素與不同類別集合之間的灰色關聯(lián)系數(shù).

步驟6,基于灰色關聯(lián)度計算模型，獲得待測系統(tǒng)與不同類別集合之間的灰色關聯(lián)度.

步驟7,基于灰色關聯(lián)度的大小獲得待測系統(tǒng)的歸屬類別，從而獲得待測系統(tǒng)的灰色聚類分析預測結果.

步驟8,預測結果是否達到預測精度要求，若不滿足，對所歸屬類別進行細化，再重復執(zhí)行步驟2-步驟7.

3 模型與算法在電力負荷預測中的驗證

電力負荷在地區(qū)經濟發(fā)展中起到至關重要的作用，因此，有效地預測出不同階段的電力負荷，并對其進行充足的供應，將對地區(qū)經濟的快速、可靠和穩(wěn)定的發(fā)展提供十分重要的支持.然而，電力負荷受到多種因素的制約，需要對這些因素進行有效的類別劃分才能夠實現(xiàn)電力負荷的有效預測.本文提出的模型將能較好地解決電力負荷預測的復雜系統(tǒng)預測分析問題.通過調研考察可知，某地區(qū)電力負荷和產業(yè)發(fā)展狀態(tài)有著必然的關聯(lián)關系，通過統(tǒng)計分析獲得近10年相關的數(shù)據(jù)序列，如表1所示.

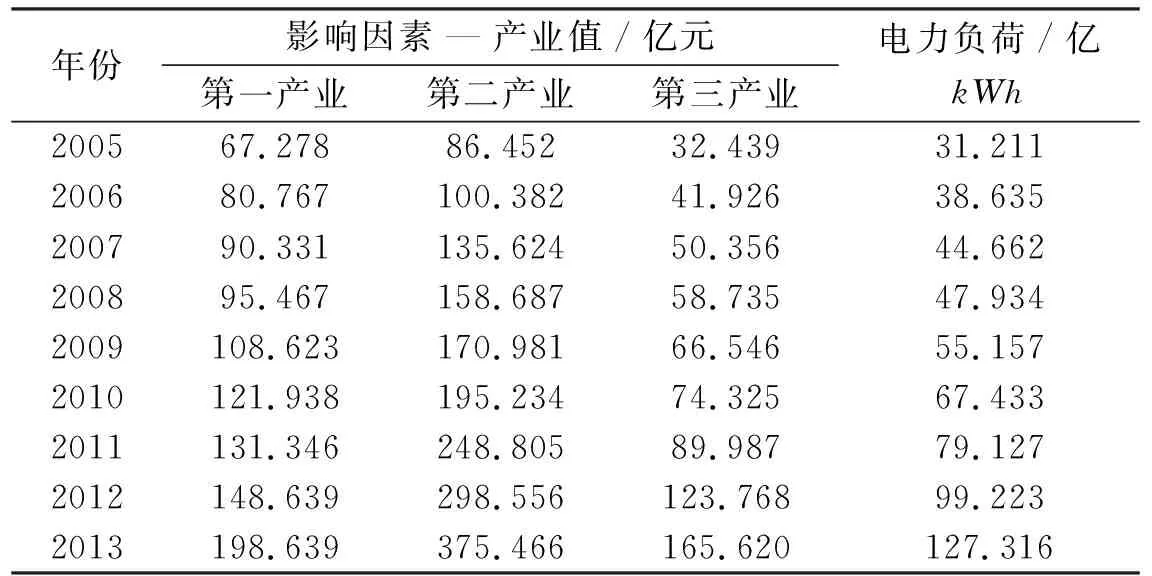
表1 電力負荷數(shù)據(jù)與產業(yè)發(fā)展狀況

為了便于建立灰色節(jié)域和灰色經典域，將表1中的數(shù)據(jù)進行轉化，以特征增長率的形式表述各個特征量，具體結果見表2.

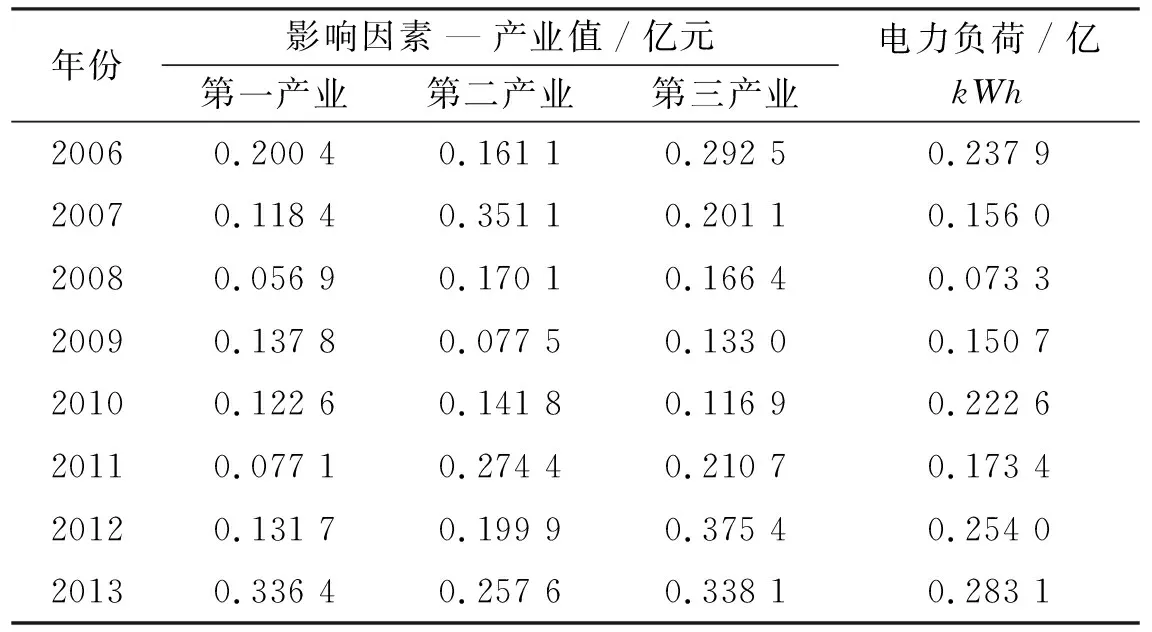
表2 電力負荷數(shù)據(jù)與產業(yè)發(fā)展量值增長率

由表2可以看出，電力負荷的增長率范圍為0.070-0.300之間，為此，按照電力負荷的增長率η(pow)將電力負荷預測類別分為4類，即：

(16)

選擇第一產業(yè)、第二產業(yè)和第三產業(yè)作為預測特征，獲得不同類別下的預測特征平均值，基于上述建立的4種電力負荷預測類別，分別構建每一種類別的灰色經典域，結果如表3所示.

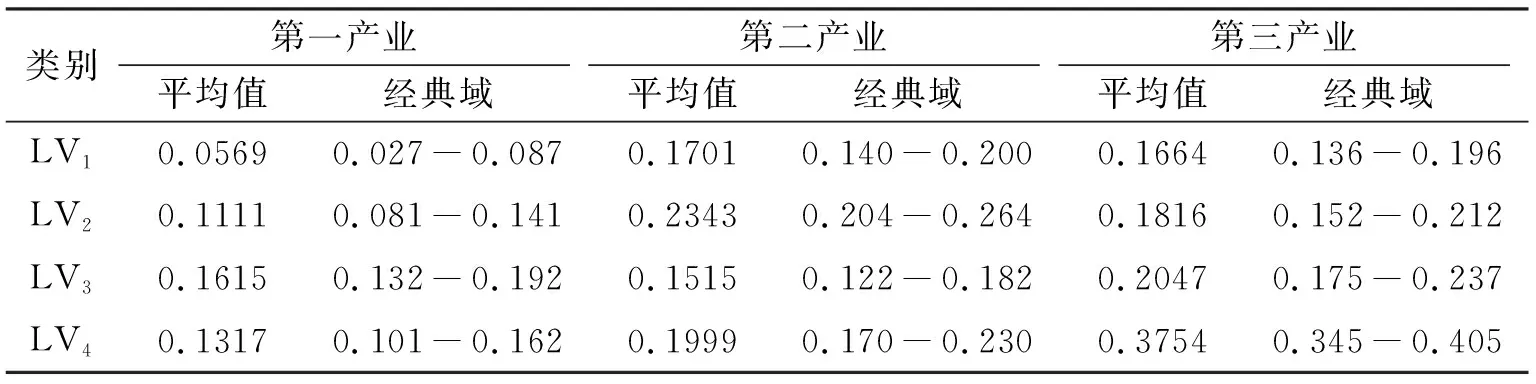
表3 電力負荷類別經典域構建

以不同類別不同類型產業(yè)的增長率經典域作為灰色數(shù)據(jù)序列的比較序列，以待測系統(tǒng)的不同類型產業(yè)的增長率作為參考序列，基于灰色關聯(lián)系數(shù)計算模型，獲得待測系統(tǒng)關于不同預測特征的灰色關聯(lián)系數(shù)，結果如表4所示.

考慮不同預測特征的權重，基于灰色關聯(lián)度計算模型，獲得待測系統(tǒng)關于不同預測特征的綜合灰色關聯(lián)度，結果如表5所示.

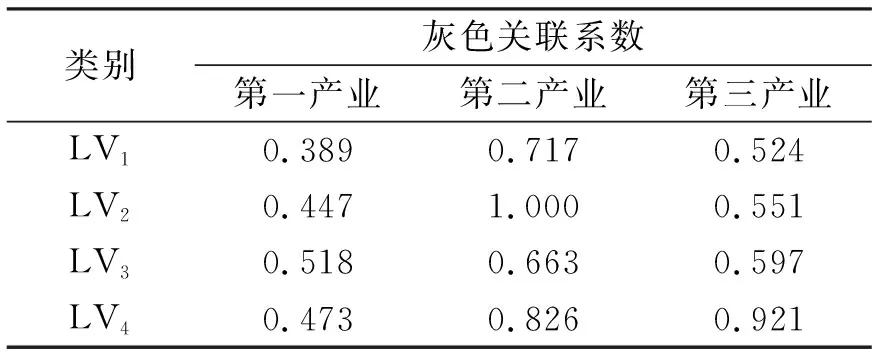
表4 待測系統(tǒng)的灰色關聯(lián)系數(shù)

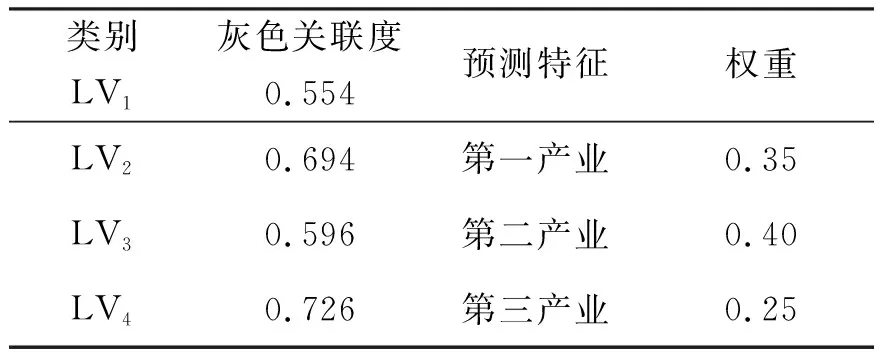
表5 待測系統(tǒng)的灰色關聯(lián)系數(shù)

由表5可以看出，待測系統(tǒng)應歸屬于類別，對應的增長率范圍為0.250<η(pow)≤0.300，電力負荷應在區(qū)間內〈124.028,128.990〉.實際的電力負荷值如表1，其量值為127.316，增長率如表2，其量值為0.283 1，可以發(fā)現(xiàn)127.316∈〈124.028,128.990〉,0.283 1∈〈0.250,0.300〉，說明實際數(shù)值均在預測范圍內，證明了模型的有效性.

4 結語

本文針對復雜系統(tǒng)的事件預測問題進行了分析研究，在灰色系統(tǒng)理論的基礎上，提出了一種基于改進的灰色聚類分析的預測模型，并在電力負荷預測的實例中進行了驗證分析，說明了模型的有效性.該模型通過構建灰色數(shù)據(jù)序列，構建預測特征的灰色經典域和灰色節(jié)域，建立預測系統(tǒng)關于預測特征與不同類別經典域之間的灰色關聯(lián)系數(shù)和灰色關聯(lián)度，進而獲得基于灰色聚類分析的預測結果.模型表征的物理意義明確，計算結果可靠，精度較高，適合于計算機智能化的實現(xiàn)，能夠為復雜系統(tǒng)智能預測的實施提供有利的支持.