基于模糊自抗擾的風電系統獨立變槳距控制
任麗娜, 劉 素, 劉福才, 張 磊
(1.燕山大學 工業計算機控制工程河北省重點實驗室,河北秦皇島 066004;2.秦皇島煙草機械有限責任公司,河北秦皇島 066318)
風能是一種安全、生態和可再生能源,變槳距風力發電機組由于對風能利用的高效性,占據了市場的主導地位[1]。變槳距控制主要有統一變槳和獨立變槳2種方式。在統一變槳控制設計過程中,假設風輪旋轉平面內風速均勻。但隨著風電機組容量的增加和葉片的加長,由風剪切和塔影效應等引起的附加載荷更加嚴重,俯仰力矩和偏航力矩等也逐漸增大,這不僅影響風電機組運行的穩定性,還會引起輸出功率振蕩,降低風力機部件的壽命[2]。因此,如何在保證發電質量的同時降低不平衡負荷具有重要的研究意義。獨立變槳控制(IPC)[3]是一種旨在穩定發電機的輸出功率、降低由不斷變化的風力條件造成的風力機負載擾動的控制方法。控制器可根據各葉片不同的受力情況得到不同的葉片槳距角,3個執行器參考不同控制量進行獨立操作,因此被稱為獨立變槳距控制器。近年出現了許多用于降低疲勞負荷、提高發電效率的風力發電機獨立變槳距控制策略,包括傳統的控制算法,如比例-積分-微分(PID)控制[4]、全狀態反饋控制[5]和擾動調節控制(DAC)[6]。現代控制算法的應用進一步提高了風力機的性能。文獻[7]中采用基于葉根載荷變換的槳距角反饋線性化獨立變槳控制策略,有效降低了動態載荷,但是對于穩定輸出功率的效果并不明顯。文獻[8]中提出了一種最優控制策略,通過對風力機葉片偏移和塔架彎曲進行優化控制,提高了發電機的輸出功率,但難以精確地建立實際運行中風電系統的數學模型。文獻[9]中提出了一種滑模控制策略,可有效地解決系統中不確定參數的變化,但較易出現抖振問題。
獨立變槳距控制一般應用于額定風速以上的恒功率控制,即輸出功率是恒定值,因此在額定風速以上的風況下,可將不影響風力機功率輸出的風速、風力機的非線性等作為干擾項。自抗擾控制(ADRC)[10]是一種處理干擾的控制算法,是基于誤差反饋的非線性控制方法,不依賴于系統精確的數學模型,可對系統的未建模動態和未知擾動作出較好的估計和補償[11]。鑒于此,為了降低風力機的不平衡負載,保證在額定風速以上的風況下風力發電機的發電質量,筆者將ADRC應用于獨立變槳距降載控制中。在實際應用中,針對多個自抗擾控制器不便操作、參數調整困難的缺點,提出了基于模糊邏輯控制(FLC)理論[12]改進的ADRC獨立變槳控制,并對閉環系統的穩定性進行了分析。最后通過與傳統PD獨立變槳、ADRC獨立變槳控制策略進行比較,驗證了模糊自抗擾控制器(FLC-ADRC)的優越性。
1 風力機描述與建模
1.1 風速模型的建立
1.1.1 風剪切風速模型
圖1給出了風速隨高度變化的示意圖。
隨高度變化的風剪切風速模型[13]通常表示為:
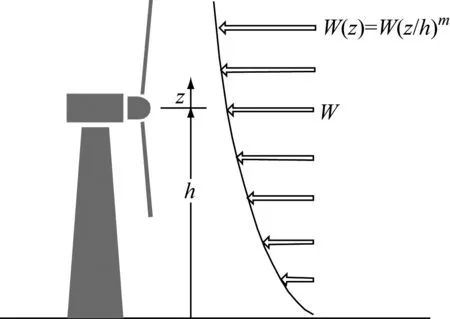
圖1 風速隨高度變化的示意圖Fig.1 Variation of wind speed with height
(1)
式中:wshear為由風剪切效應導致的風速變化擾動量;W為輪轂中心高度h處的平均風速;z為風力機葉片高度;m為風剪切系數。
1.1.2 塔影效應風速模型
由于塔架對氣流造成堵塞,在塔架上游和下游來流速度均減小,稱為塔影效應,可表示為:
(2)
式中:wtower為由塔影效應造成的風速變化擾動量;W0為空間平均風速;a為塔架半徑;H為槳葉微元到塔架y軸的軸線距離;L為槳葉微元到塔架x軸的軸線距離。
塔影效應是對作用在葉片上的風速的影響,只產生于下半風輪掃掠面,模型建立較為復雜,因此將塔影效應的風速模型看作未知的外部干擾。
1.2 風力機模型的建立
為了建立有效的風力機獨立變槳控制器,筆者采用的獨立變槳距控制系統模型如下:
(3)
式中:A為系統的狀態矩陣;B為控制輸入矩陣;u為控制輸入向量矩陣,u=[β1β2β3]T,其中β1、β2和β3分別為3個葉片的輸入槳距角;Γ為風速變量輸入矩陣;wshear為分別作用在3個葉片上的風剪切風速矩陣,wshear=[wshearwshearwshear]T;wv為分別作用在3個葉片上的塔影效應干擾矩陣,wv=[wv1wv2wv3]T;y為系統模型的狀態輸出矩陣;x為狀態變量矩陣,x=[x1x2x3x4x5x6x7x8]T,其各個狀態量含義如表1所示。
根據非線性風力發電機獨立變槳距控制系統的動力學方程,其狀態空間方程轉化形式為[14]:
(4)
式中:Irot為轉子轉動慣量;Mij、Kij和Cij分別為系統的質量、剛度和阻尼項,其中i,j=1,2,3,5;ζi(i=1,2,3,4)為轉子轉矩關于槳距角的偏導數;ζbi(i=1,2,3,4)為葉片空氣動力關于葉片槳距角的偏導數;r為轉子轉矩對轉速的導數;[w1w2w3]T為包含風剪切的風速輸入變量,其中w1、w2和w3分別為3個葉片承受的風速;a為轉子轉動加速度;ab為每個葉片的一階偏移速度與作用在葉片上風速的關系。

表1 狀態變量Tab.1 State variables
2 獨立變槳控制器設計
為了減小葉片疲勞載荷和穩定輸出功率,針對3個葉片及轉子分別設計FLC-ADRC獨立變槳控制器,盡可能減小葉片偏移與功率波動,即使狀態變
量的期望值x*=0。將作用于風力機葉片間的耦合、風速和其他不確定因素均歸結為未知干擾,通過擴張狀態觀測器(ESO)對干擾進行實時跟蹤估計,并利用非線性誤差反饋控制律給予補償,消除其影響;將模糊邏輯控制應用于自抗擾控制器參數的整定,得到模糊自抗擾獨立變槳控制器。為簡單起見,筆者以葉片1為例,給出詳細的設計步驟,其余狀態變量控制器設計類似。
2.1 自抗擾控制器設計
2.1.1 擴張狀態觀測器設計
以二階非線性控制對象葉片1為例,設計擴張狀態觀測器。葉片1的狀態空間表達式如下:
(5)
式中:β1為葉片1的控制槳距角。
為設計擴張狀態觀測器,將葉片1的狀態空間表達式轉化為:
(6)
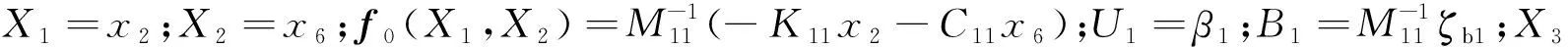
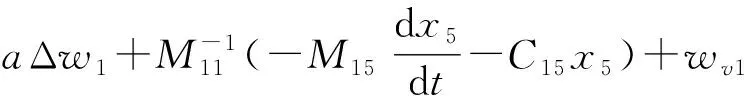
(7)
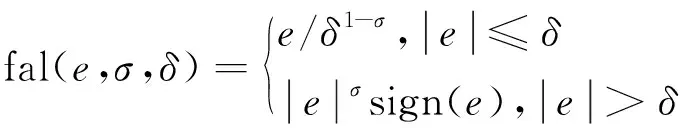
(8)
式中:Z1、Z2和Z3分別為X1、X2和X3的觀測值;β01、β02和β03為相應的觀測增益;e1=Z1-X1;B01為B1的大致估計值;e為變量;σ和δ均為給定的參數,其中σ∈(0,1),δ是限制原點附近增益的小數。
為便于表達,用f1(e1)代替fal(e1,σ1,δ),f2(e1)代替fal(e1,σ2,δ)。考慮式(5)和式(6),可得到跟蹤誤差系統:
(9)
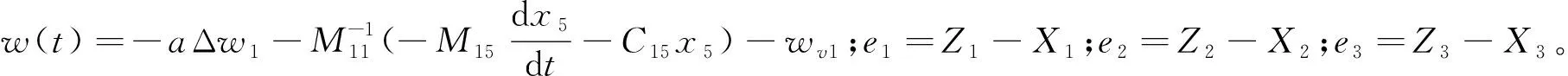
2.1.2 非線性控制律
定義葉片1給定輸入與擴張狀態觀測器觀測值之間的誤差為:
(10)
式中:r1為葉片1給定偏移量V1與偏移量觀測值Z1的誤差;r2為葉片2給定偏移速度V2與偏移速度觀測值Z2之間的誤差。
U1=(KP1+ΔKP1)fal(r1,σ3,δ1)+
(KD1+ΔKD1)fal(r2,σ4,δ2)-(Z3+f0)/B01
(11)
式中:KP1和KD1分別為葉片1自抗擾獨立變槳控制器的偏移量和偏移速度增益;ΔKP1和ΔKD1為從模糊邏輯控制器中所得的增益微調。
2.2 自抗擾控制器參數整定
針對風力機參數的不確定性,手動調節各參數大小不利于實際操作。因此,引入模糊控制器,利用模糊規則,在線整定自抗擾控制器參數,以滿足不同狀態下的參數要求,設計4種不同的FLC應用于風力機變槳控制中,選擇用于控制風力機的第1個葉片進行詳細闡述。

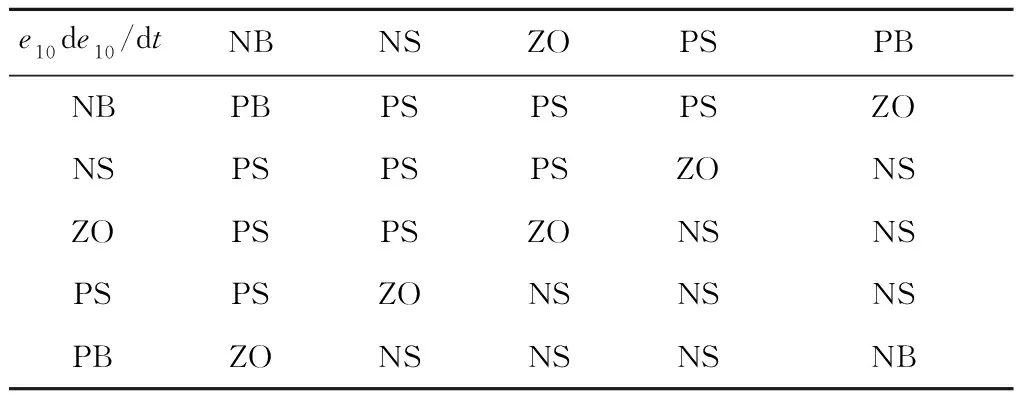
表2 ΔKP1的模糊控制規則Tab.2 Fuzzy control rule of ΔKP1
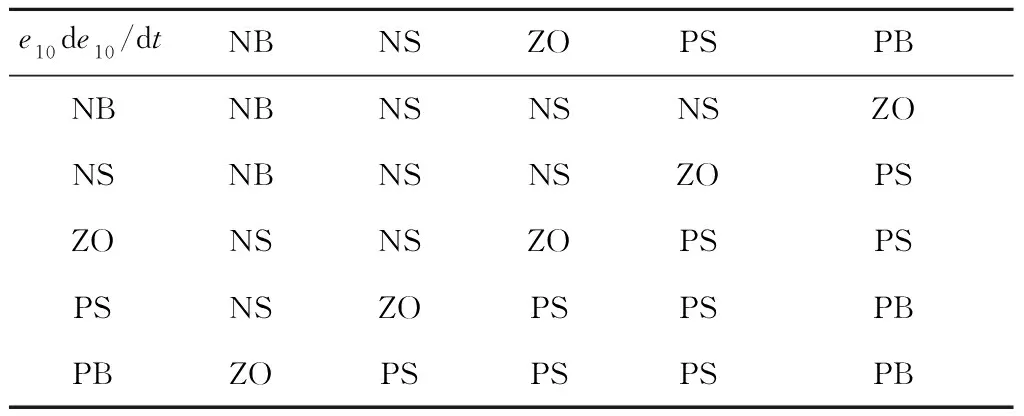
表3 ΔKD1的模糊控制規則Tab.3 Fuzzy control rule of ΔKD1
利用上述獨立變槳距FLC-ADRC控制器設計方法,針對葉片1提出的控制律如下:
U1=(KP1+ΔKP1)fal(r1,σ3,δ1)+
(12)
圖2為風力機模糊自抗擾控制系統框圖,其中FLC-ADRC1為上述詳細設計結構圖,UD為作用在風力機上的風速變量矩陣,UD1為作用在葉片1上風速變量的總和。
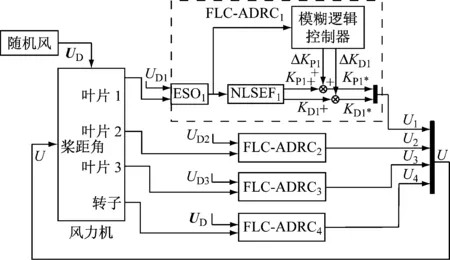
圖2 風力機控制系統框圖Fig.2 Block diagram of the wind turbine system
2.3 基于模糊自抗擾控制器的系統穩定性分析
定理1:考慮式(6)描述的閉環控制系統,存在式(11)中合適的參數KP1+ΔKP1和KD1+ΔKD1,保證閉環系統穩定,即保證系統的實際輸出值X1和X2分別跟蹤給定值V1和V2。
證明:對于閉環控制系統,定義給定與系統實際輸出之間的誤差為:
(13)
式中:s1為葉片1給定偏移量V1與實際輸出偏移量X1之間的誤差;s2為葉片1給定偏移速度V2與實際輸出偏移速度X2之間的誤差。
(14)
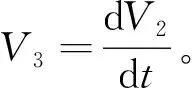
根據式(10)和式(13),可得到如下形式:
(15)
選擇系統(式(15))中的Lyapunov函數[15]:
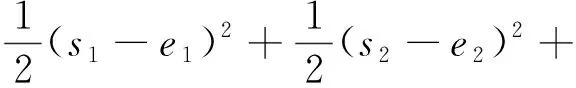
(s1-e1)(s2-e2)
(16)
(17)
代入式(11)可得:
V3-X3+Z3-B01(KP1+ΔKP1)fal(r1,σ3,δ1)-
B01(KD1+ΔKD1)fal(r2,σ4,δ2)=V3+e3-
B0(KP1+ΔKP1)fal(r1,σ3,δ1)-
B01(KD1+ΔKD1)fal(r2,σ4,δ2)
(18)
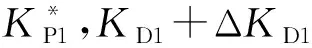
(s1-e1)(s2-e2)+β01e1(s1-e1)+(s2-e2)2+
(s1-e1+s2-e2)(V3+β02f1(e1))+
β01e1(s2-e2)
(19)
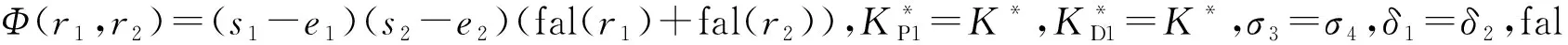
Φ(r1,r2)≥0
(20)
根據文獻[16],e1、e2和e3有界,且在實際應用中V3、s1和s2也有界。由于r1=s1-e1,r2=s2-e2,因此r1和r2有界。設:
M=|(s1-e1)(s2-e2)+β01e1s1+(s2-e2)2+
(s1-e1+s2-e2)(v3+β02f1(e1))+
β01e1(s2-e2)|
(21)
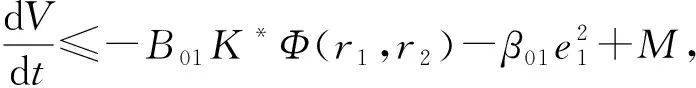
(22)
因此式(13)穩定,X1和X2分別收斂于V1和V2,即輸出值與給定值之間的誤差趨近0,提出的模糊自抗擾控制器保證了式(6)(閉環系統)的穩定性。
3 仿 真
仿真采用的5 MW風力機參數[18]見表4。采用Matlab仿真驗證提出的風力機獨立變槳控制器的控制性能。工作區域集中在額定風速以上,其目標是使轉子速度和葉片波動最小化。圖3給出了風力機輪轂高度處風速在15~20 m/s內的變化。圖4給出了作用在3個葉片上的隨機風速變化。在FLC-ADRC控制策略作用下3個葉片偏移量見圖5。
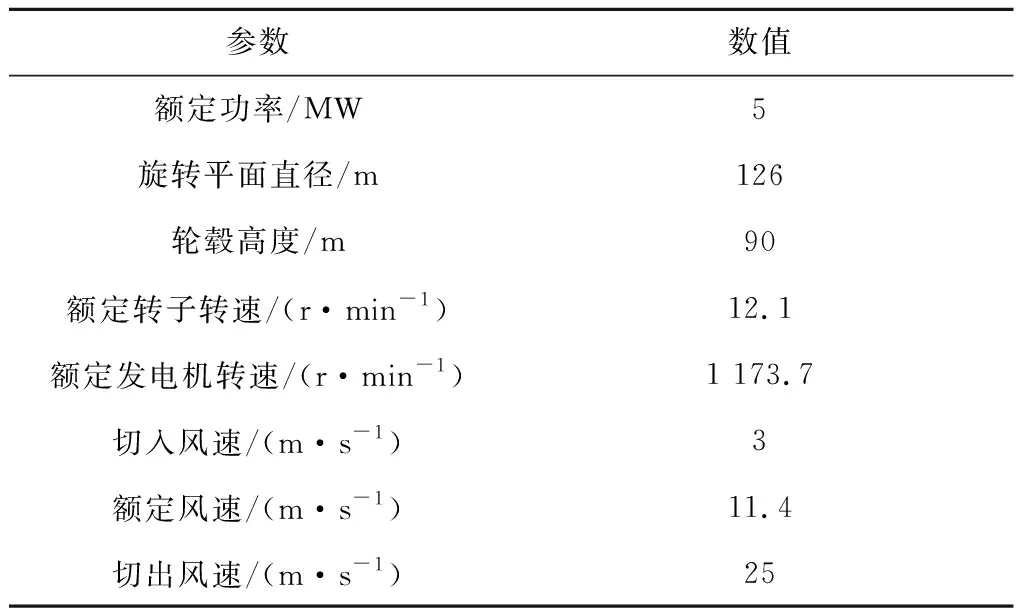
表4 5 MW風力機參數Tab.4 Parameters of the 5 MW reference wind turbine
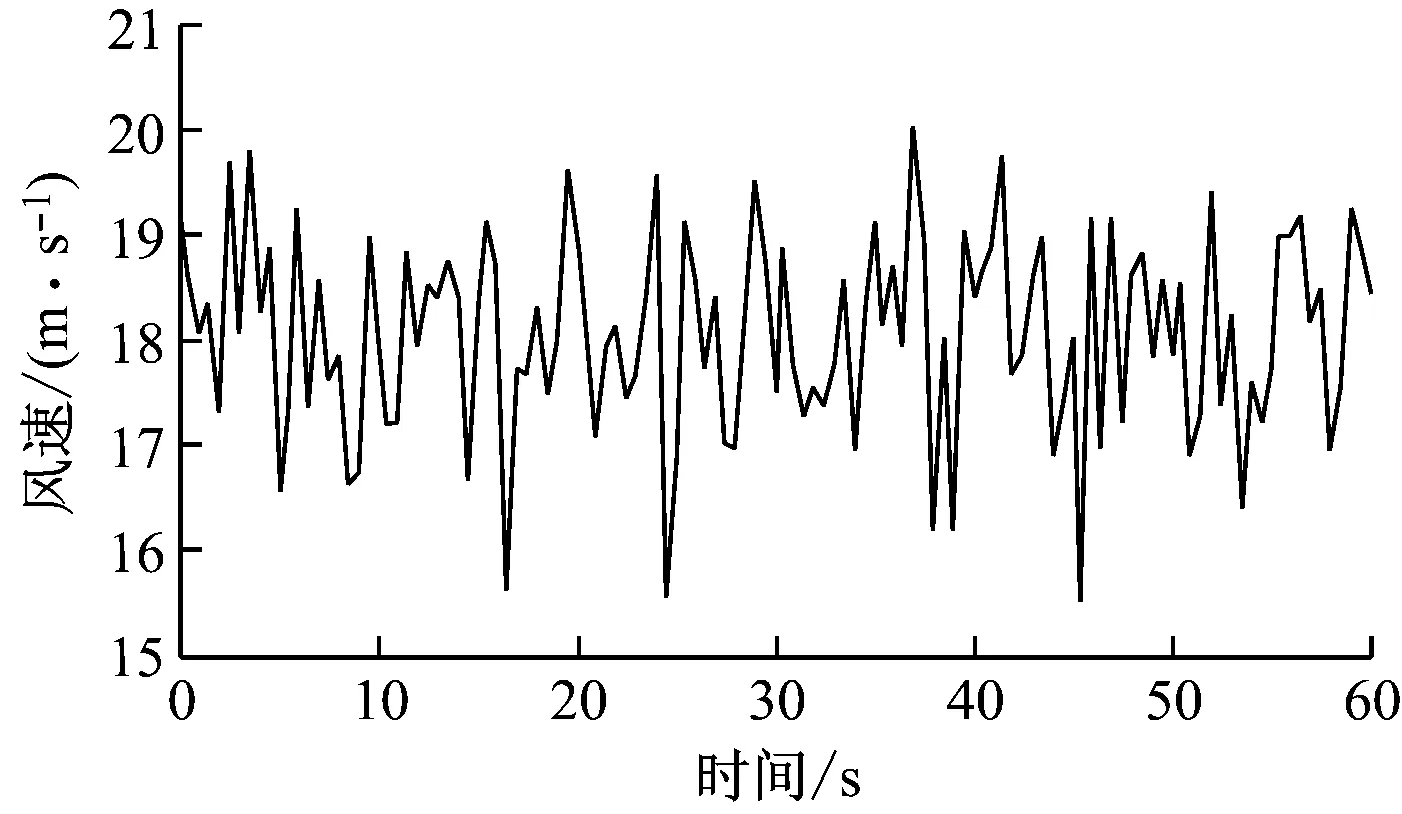
圖3 輪轂高度處的風速Fig.3 Hub-height wind speed
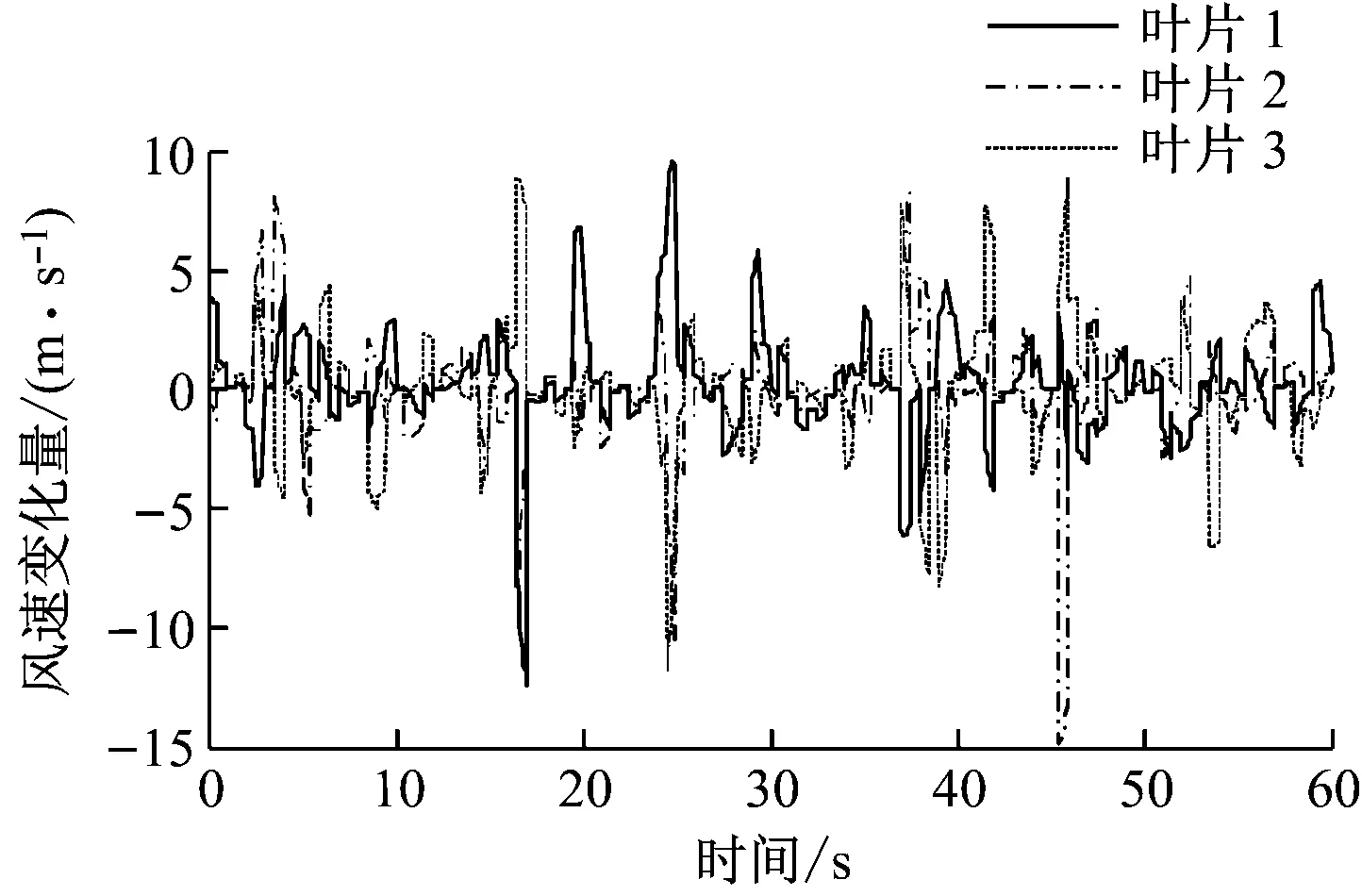
圖4 每個葉片的風速Fig.4 Wind speed variation of each blade
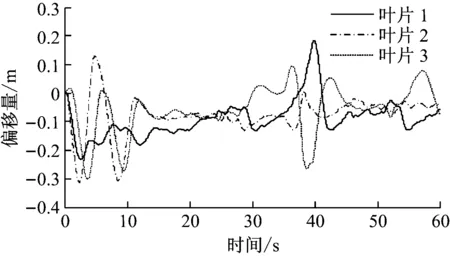
圖5 每個葉片的偏移量Fig.5 Offset of each blade
以葉片1為例,圖6給出了在FLC-ADRC控制策略下葉片1的葉尖波動和速度變化。由圖6可知,根據ESO可很好地估計出葉尖偏移量和偏移速度,偏移速度觀測值與輸出軌跡幾乎一致。圖7給出了FLC-ADRC、ADRC和PD這3種不同控制方式下仿真結果的比較。圖7(a)和圖7(b)分別為不同控制方式下風力機轉子的轉速和輸出功率波動,3種控制方式均能較好地抑制轉子的轉速波動,保證系統的輸出功率較為穩定。由圖7(c)和圖7(d)可知,葉片尖端偏移量和速度波動的幅度控制在較小范圍內,具有較好的動態性能,風力機的疲勞載荷減小,風力機部件的損壞也減少。在應用過程中,FLC-ADRC控制策略更適用于難以建立精確數學模型、運行過程中受隨機風速干擾影響嚴重的風力機系統。

(a) 葉片1的偏移量

(b)葉片1的偏移速度圖6 ESO狀態跟蹤曲線Fig.6 Tracing curve of ESO state
4 結 論
(1)相較于統一變槳,獨立變槳能夠對各葉片的槳距角分別控制,進而減小模型的非線性和外界不可知干擾造成的不平衡載荷。
(2)應用ESO可對風力機的非線性和隨機風速等不可知干擾進行準確估計,應用誤差狀態反饋控制器使不可知干擾得到有效補償處理。
(3)應用模糊邏輯理論對參數進行自整定,解決了多個自抗擾控制器存在參數難以調整的問題,簡化了調參過程,提高了自抗擾控制器性能。
(4)將提出的控制策略分別與PD控制策略、ADRC控制策略進行Matlab仿真對比,發現在額定風速以上的風況下應用基于模糊邏輯的自抗擾控制器能更有效地保證風力機的發電質量,抑制葉片的偏移,延長風力機的使用壽命。
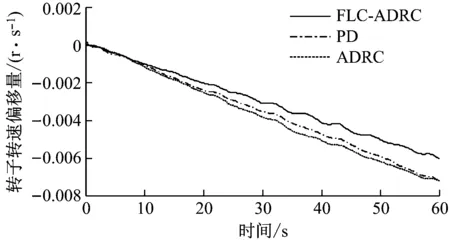
(a)轉子轉速波動
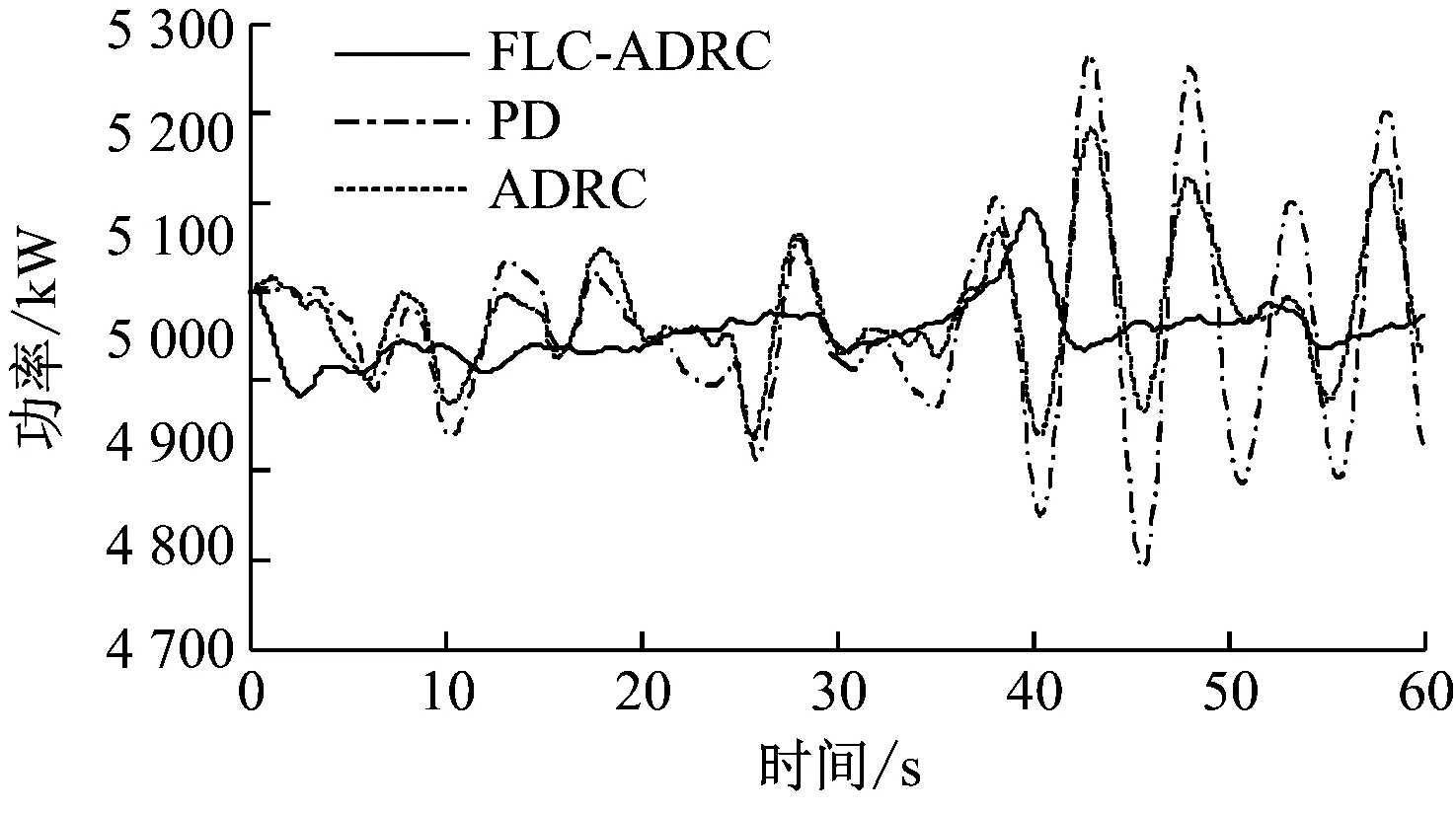
(b)功率
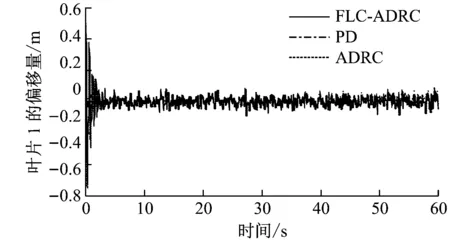
(c)葉片1的偏移量
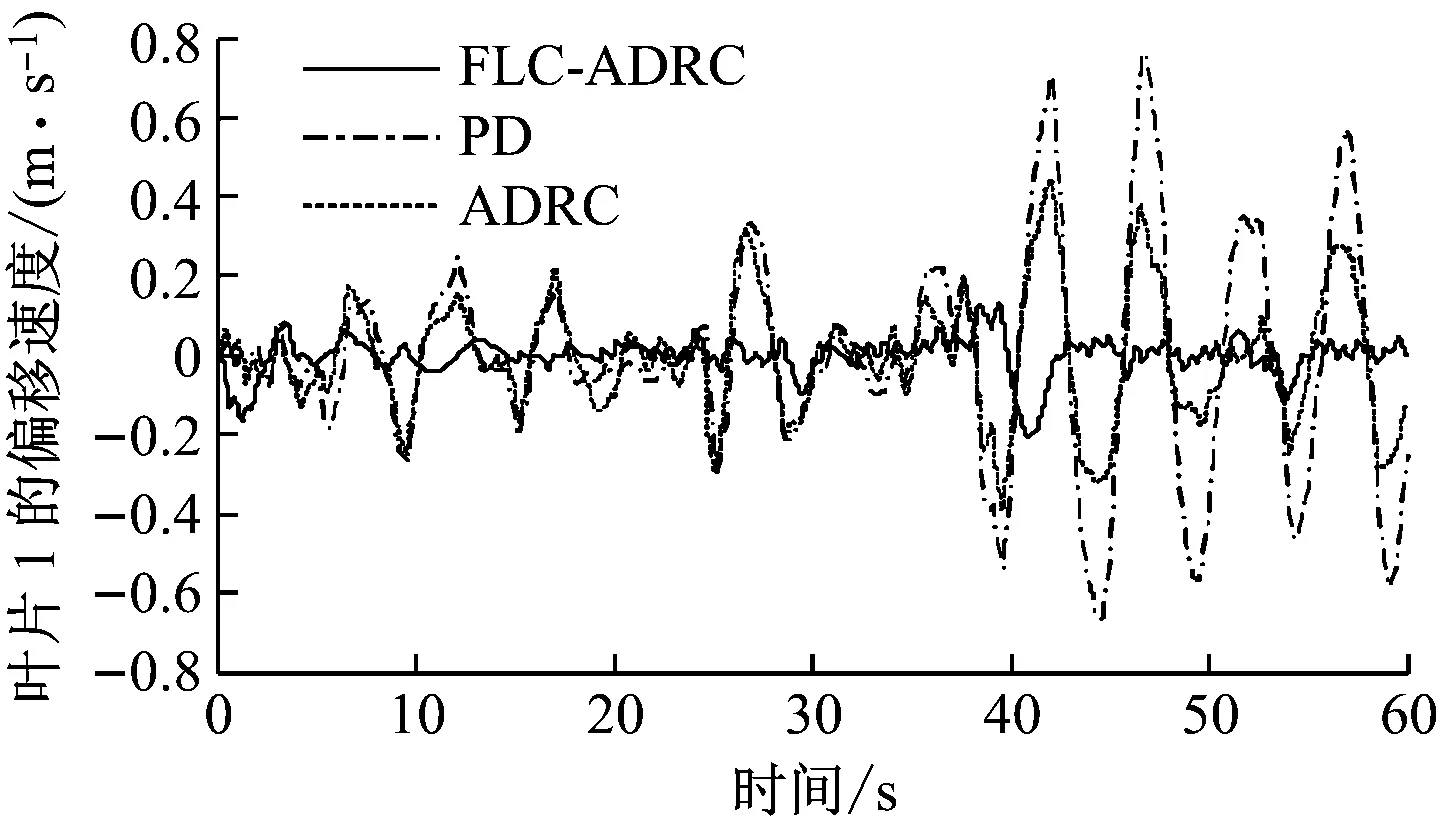
(d)葉片1的偏移速度圖7 FLC-ADRC、ADRC和PD仿真結果比較Fig.7 Simulation results of the FLC-ADRC, ADRC and PD

