考慮SSI效應的風力機塔架地震動力響應時頻特性分析

劉中勝， 楊 陽， 李 春,2， 鄒錦華

(1. 上海理工大學 能源與動力工程學院， 上海 200093；2. 上海市動力工程多相流動與傳熱重點實驗室， 上海 200093)

我國風能資源的整體特點是分布廣、不穩定和能量密度相對較低[1]。風能資源豐富的東南沿海和“三北”地區均位于地震多發地帶，這些區域的風場風力機極易受到地震載荷的影響。地震具有很強的不可預見性和突發性，結合國內外風力機結構抗震設計的理論研究和工程應用需求，風力機系統結構地震動力響應特性分析已成為當前亟待解決的重要課題[2]。隨著風力機的大型化發展，在時域非定常和空間非均勻的湍流風中葉片與塔架等細長柔性彈性體結構氣動彈性的非線性現象十分明顯[3-4]。此外，如果同時受到地震載荷的激勵作用，很可能導致風力機塔頂振動失穩和塔基結構被破壞[5]。因此，對于提高風力機結構精細化設計和系統運行可靠性控制來說，研究大型風力機塔架在風-震耦合工況下的動力響應具有重要意義。關于地震激勵下風力機塔架的動力特性，國內外學者進行了大量的相關研究。根據隨機地震動物理模型可生成加速度,賀廣零等[6]建立了風力機“槳葉-塔體-基礎”一體化有限元模型，發現土-構耦合(SSI)效應會在一定程度上增大結構響應幅值。賀廣零[7]建立了SSI模型，通過確定彈簧振子的剛度模擬出塔基處的地震載荷，發現SSI效應會增加塔基與地基連接的柔度，影響塔架的振型和振動頻率。周勃等[8]基于有限元分析方法研究了風力發電機塔架的動力特性和影響因素，確定了結構的有限元模型和劃分網格的方法。祝磊等[9]采用Ansys有限元軟件的Beam188單元建模，運用時程分析法研究不同強度地震激勵下風力機結構的非線性動力響應規律。Nuta等[10]在不同載荷作用下對風力機結構的動力特性進行了較為詳細的分析，確定了結構的破壞位置及破壞形式，從而有效地進行加強與檢測，以保證風力機的結構安全。Bazeos等[11]建立了風力機塔架殼體模型，分析地震載荷對風力機結構動力響應的影響，并初步考慮了土-構相互作用的影響。Tanabe等[12]對600 kW風力機進行了動力分析，發現在罕遇地震激勵下塔體的彎矩超過了初始彎矩。Lavassas等[13]基于有限元法計算出風力機鋼制圓柱型塔架在地震載荷作用下的結構強度。

以上研究均簡化甚至忽視了風載荷對風力機結構強度的影響。而實際上隨著風力機的大型化發展，風載荷效應明顯增大，氣動載荷對風力機結構的影響不可忽視。對于現代大型化風力機的動力學仿真模擬來說，研究表明地震載荷和氣動載荷的耦合作用對風力機整機動力學特性的影響非常重要[14-15]。

筆者以美國可再生能源實驗室(NREL)的5 MW風力機[16]為計算樣機，基于Wolf方法[17]建立了SSI模型，綜合考慮了結構的非線性特性和不同場地土質對地震動的放大效果，研究風力機塔架在不同地震動作用下的時頻特性，為風力機結構抗震設計提供了理論參考。

1 仿真模型及參數

1.1 研究對象

采用NREL的5 MW風力機[16]作為研究對象，其主要參數見表1。

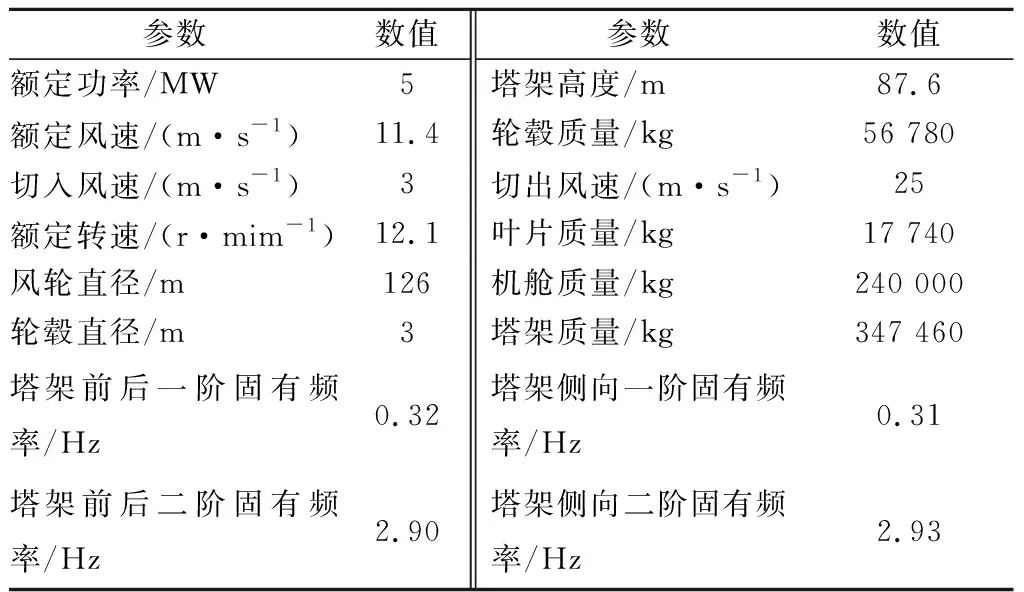
表1 NREL 5 MW風力機主要參數Tab.1 Main parameters of the NREL 5 MW wind turbine

1.2 風力機坐標系

筆者主要研究在不同場地土質下地震對風力機塔架動力響應的影響。為方便計算，在風力機上建立2個相對坐標系，分別為地基坐標系{o,x,y,z}和塔頂坐標系{o′,x′,y′,z′}，風力機模型及結構計算坐標系的自由度如圖1所示。

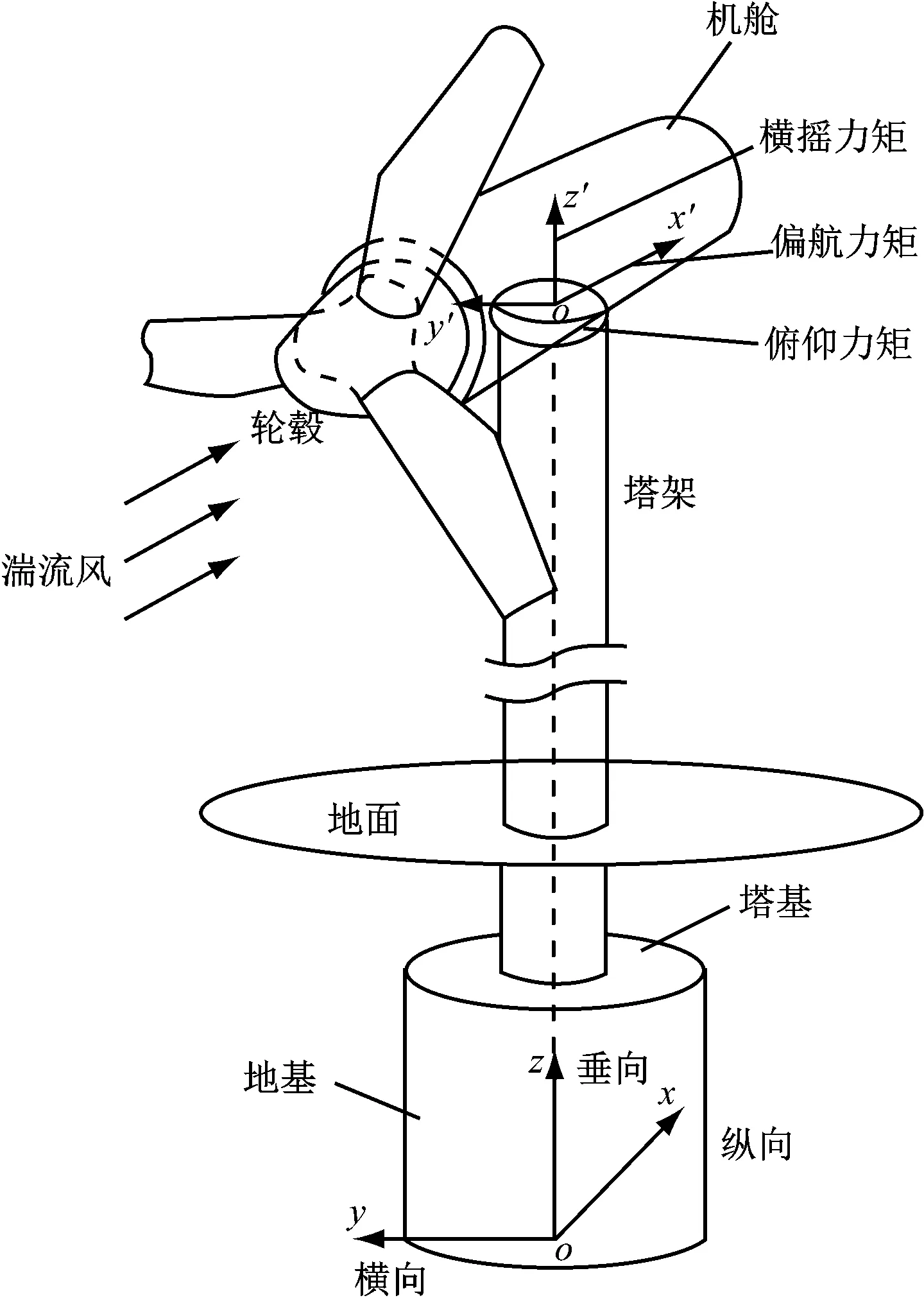
圖1 風力機模型及計算坐標系Fig.1 Model and coordinate system of the wind turbine

1.3 地震動仿真模型

基于Wolf方法建立風力機基礎平臺與土地間的耦合作用模型。將地震載荷與結構振動的耦合作用等效為彈簧振子，通過定義彈簧振子的阻尼和剛度，即可將地震運動轉化為相應的地震載荷，SSI模型如圖2所示。

各個方向的阻尼C和剛度K通過式(1)和式(2)進行計算。

(1)

(2)

式中：Kx和Ky分別為縱向和橫向的剛度；Kz為垂向的剛度；Cx和Cy分別為縱向和橫向的阻尼；Cz為垂向的阻尼；Gs、μs和ρs分別為土體的切變模量、泊松比和密度；Rs為基礎平臺的半徑。

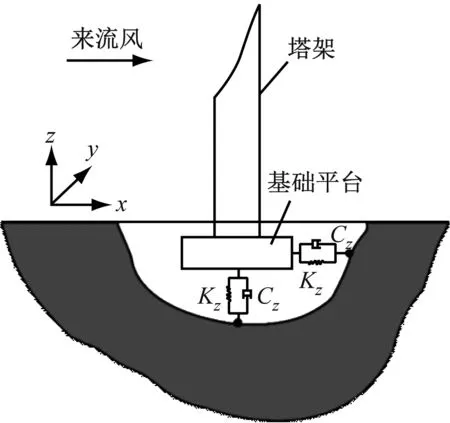
圖2 SSI模型Fig.2 SSI model of the wind turbine platform

1.4 仿真流程

風場仿真軟件、地震和動力學模擬軟件均采用NREL的計算機輔助設計包軟件。基于風力機多體動力學仿真開源軟件Fast，通過子模塊TurbSim、AeroDyn和Sesimic建立風力機地震動力學仿真模型，具體步驟如圖3所示。

2 塔架外部激勵

2.1 氣動載荷

在y″和z″方向上風場設計計算各有11個網格點，風場示意圖如圖4所示。

額定風速為11.4 m/s，極限風速為25 m/s(切出風速)，通過TurbSim[18]模擬風力機的運行環境。通過經典Von Karman湍流風譜模型對功率譜進行逆快速傅里葉變換，繼而得到風速的波動。Von Karman湍流風譜模型定義為[19]：

(3)

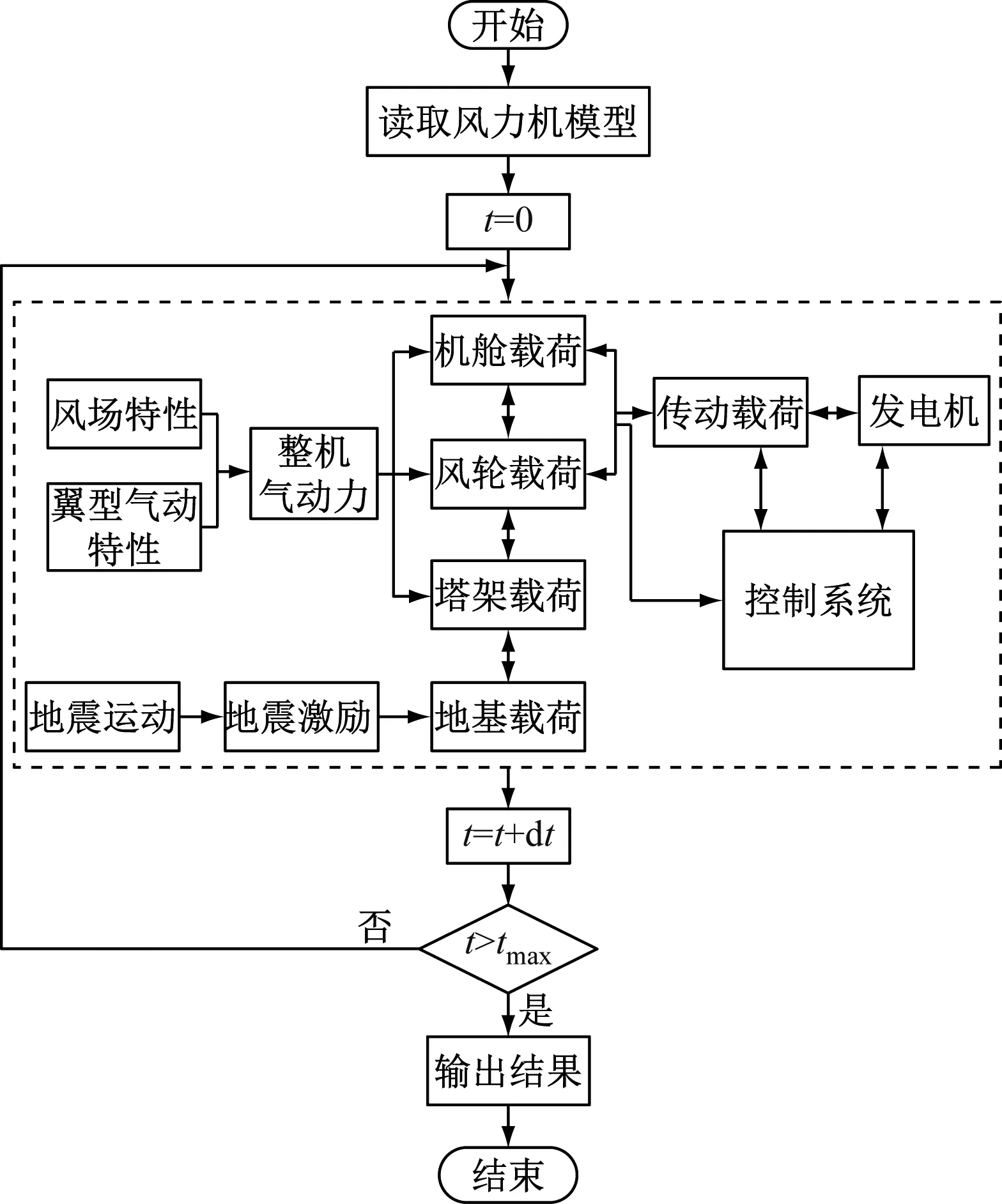
圖3 地震動力學仿真流程Fig.3 Flow chart of seismic dynamics simulation

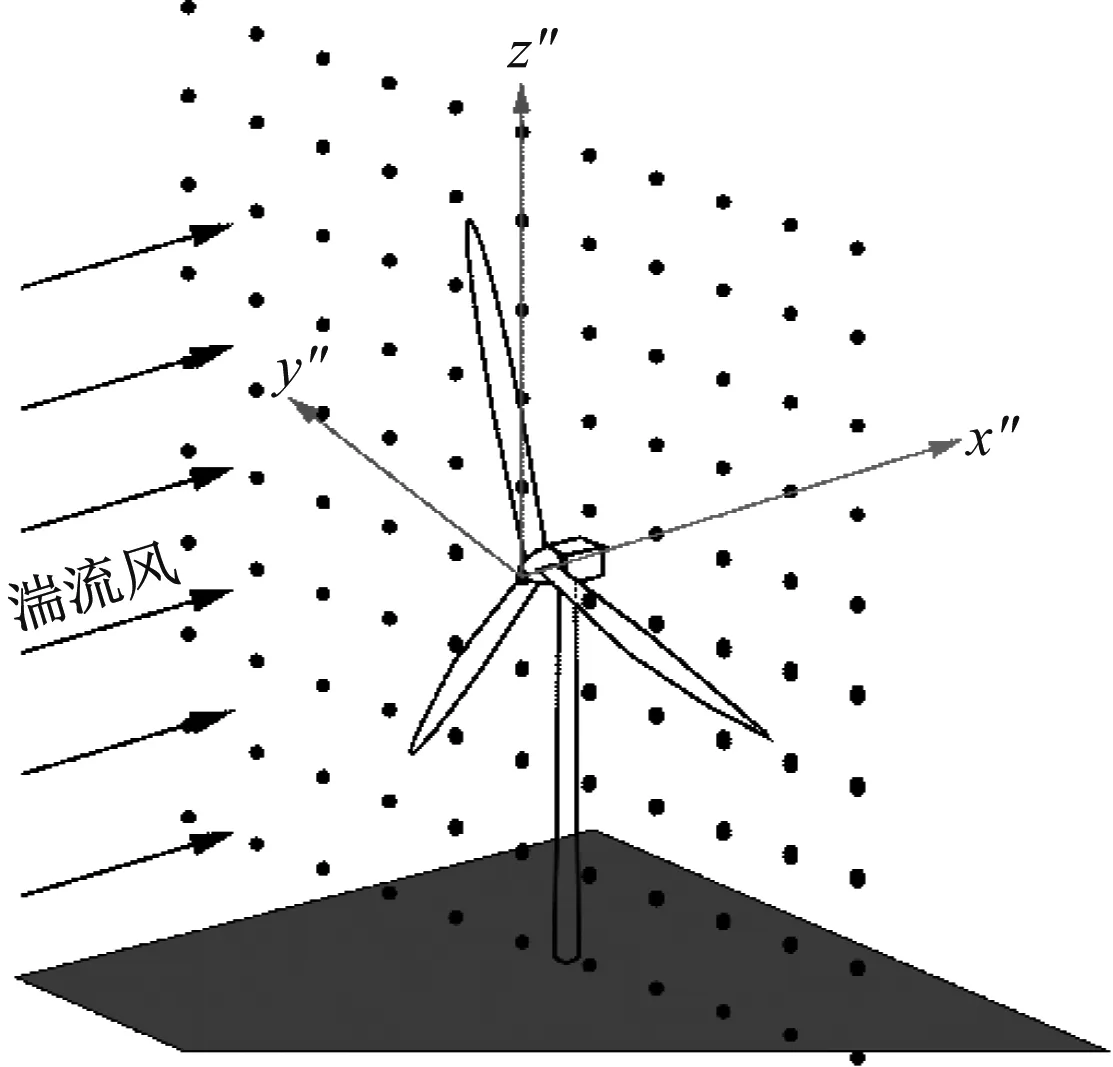
圖4 風場計算區域及網格分布Fig.4 Computational domain and grid distribution of the wind field

(4)

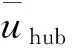
塔架某一高度h處風作用于塔架產生的氣動載荷可表示為[20]：

(5)

式中：H為塔架高度；V(h)為高度h處的風速；D(h)為高度h處塔架的外徑；C(h)為阻力系數；δ為陣風因子。

通過TurbSim模擬u、v和w這3個方向的風速，基于Matlab的數據處理和繪圖功能，計算得到湍流風場風速變化，如圖5所示。

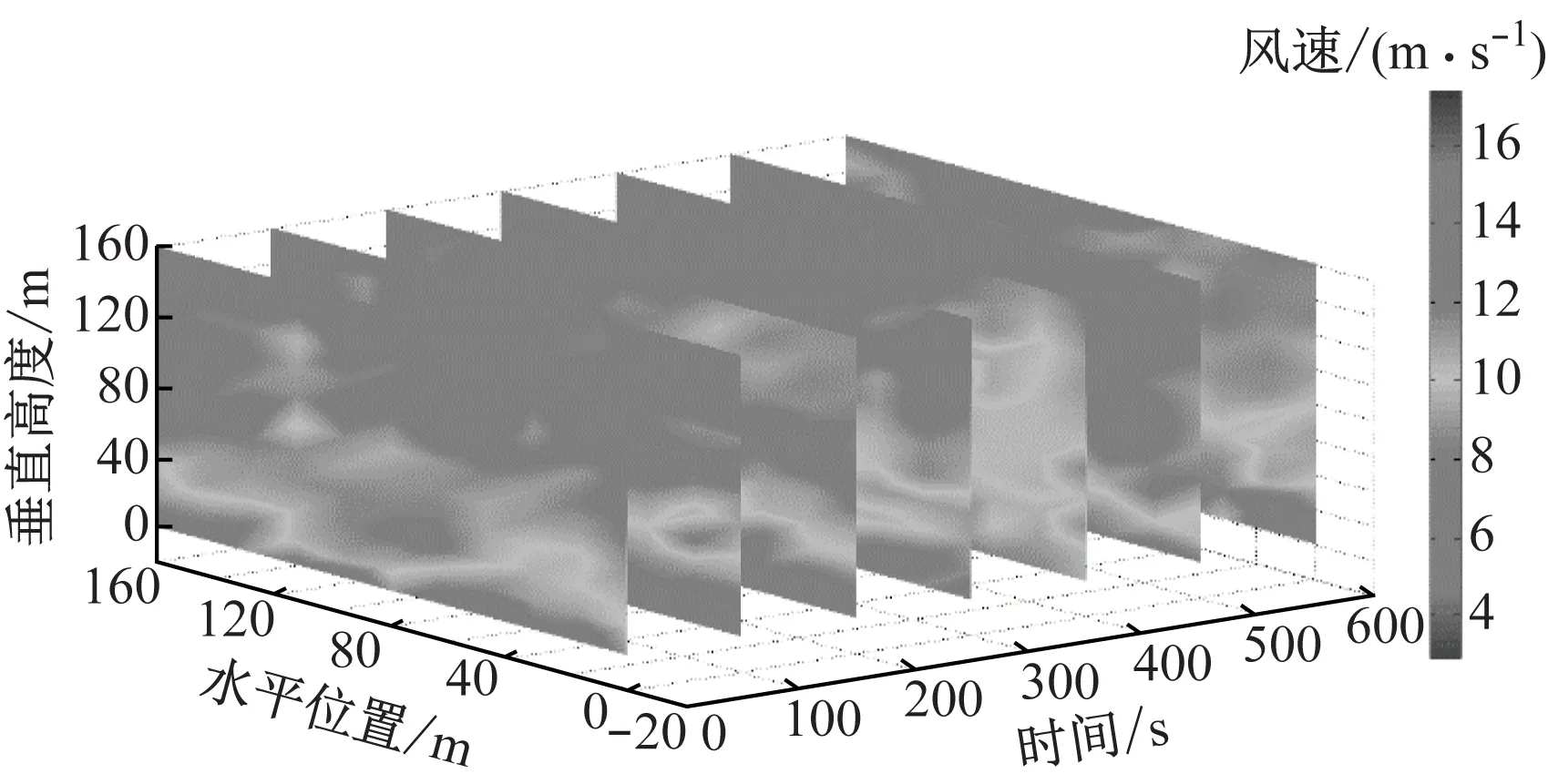
圖5 風場風速變化Fig.5 Wind speed distribution in the wind field

2.2 地震反應譜及地震載荷

地震載荷以加速度的形式作用于風力機塔架基底[21]，根據抗震設計規范定義的反應譜生成加速度。圖6為根據GB 50011—2010 《建筑抗震設計規范》[22]定義的標準地震反應譜，其中αmax為地面設計加速度的峰值；γ為衰減系數；η1為直線下降段的斜率調整系數；Tg為特征周期；η2為阻尼調整系數；T為結構自振周期。

圖6 地震反應譜示意圖Fig.6 Schematic diagram of the response spectrum

當結構阻尼比ξ不為5%時，地震影響系數曲線的阻尼修正系數和形狀參數應符合標準規定。

曲線下降段的衰減系數γ按下式確定：

(6)

直線下降段的斜率調整系數η1(當η1小于0時取0)按下式確定：

(7)

阻尼調整系數η2(當η2小于0.55時取0.55)按下式確定：

(8)

式中：ξ為結構阻尼比，取ξ=5%。

我國幅員遼闊，區域土質差異性較大。其中，東南沿海地區以軟土為主；硬黏土主要分布在南方，以貴州和云南最為典型；巖土主要分布在廣西[23]。筆者研究場地為軟土、硬黏土和巖土3種不同土質時風力機結構的動力響應，3種土質對應的物性參數[24]如表2所示。

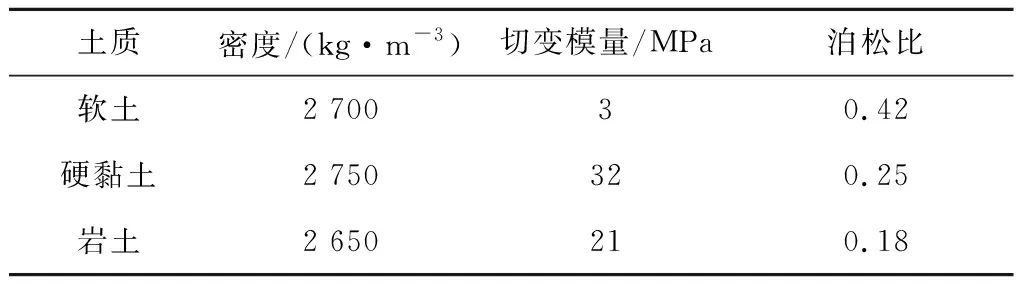
表2 3種不同土質的物性參數Tab.2 Physical properties of three different soils

參考GB 50011—2010 《建筑抗震設計規范》[22]，根據場地條件和風力機結構抗震強度要求，選取合適的特征周期Tg和地面設計加速度峰值αmax，如表3和表4所示。

表3 特征周期取值Tab.3 Characteristic period values

表4 地面設計加速度峰值Tab.4 Design values of maximum ground acceleration

風力機抗震設防烈度為8度、場地土質為軟土時對地震設計加速度反應譜進行模擬[25]，可得到人工合成的地震加速度，如圖7所示。對已獲得的人工合成地震加速度進行譜分析，可回歸為擬合的設計加速度反應譜(匹配譜)，并與目標譜進行比較，如圖8所示。

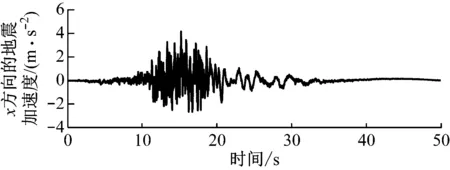
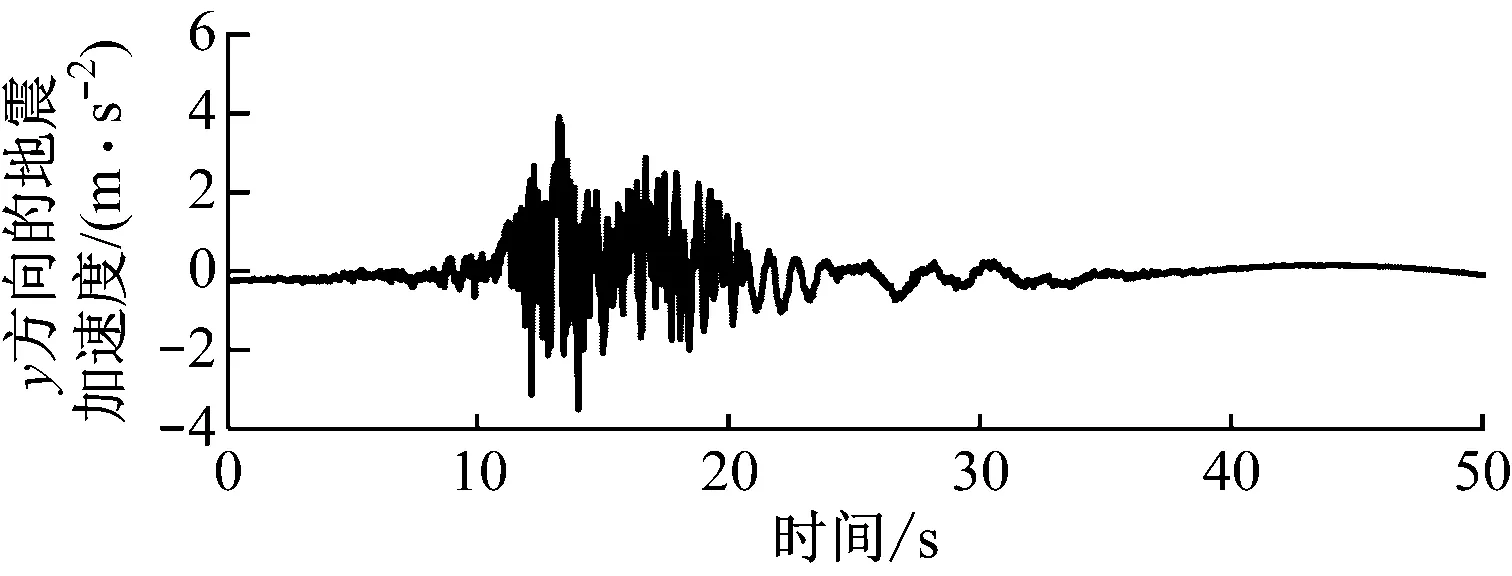
圖7 人工合成的地震加速度Fig.7 Acceleration of simulated earthquakes

由圖8可知，目標譜和匹配譜的誤差很小，最大誤差不超過10%，絕大部分的誤差在2%左右。這表明匹配譜與目標譜的吻合較好，證明人工合成地震的有效性和科學性。

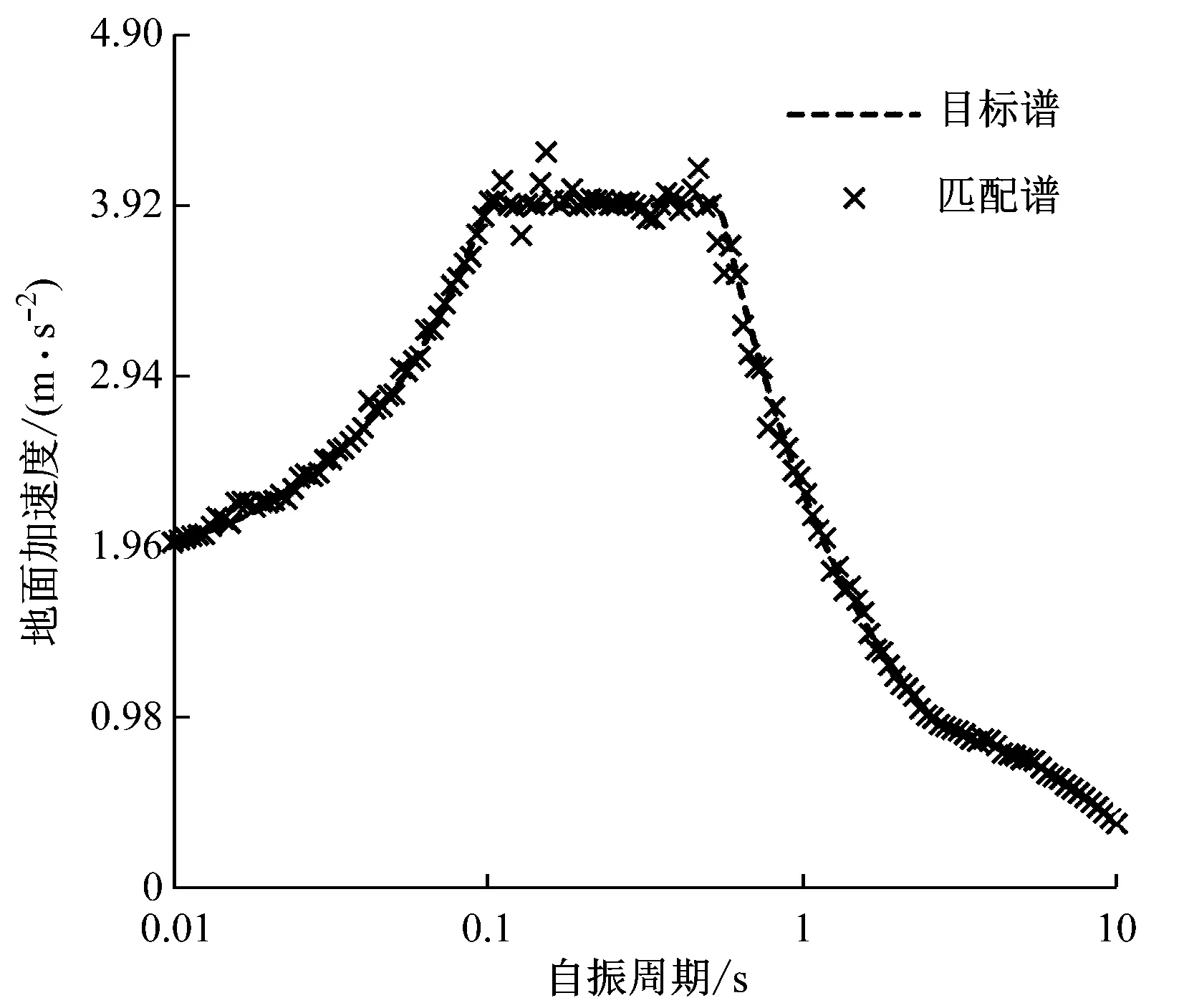
圖8 匹配譜和目標譜的比較Fig.8 Comparison between matching and target spectrum

3 結果與分析

風力機在正常工況下運行，每個算例的仿真時間為600 s，時間步長為0.002 s，在400 s時加入地震，持續時間為50 s。

3.1 時域分析

采用時域分析法研究不同工況下風力機塔架的動力響應，圖9給出了當風-震耦合作用、風單獨作用與地震單獨作用時風力機塔頂側向位移的變化曲線。

由圖9可知，在地震激勵及不同場地土質下塔頂側向位移曲線的變化趨勢基本一致，但響應幅值存在差異。由圖9(a)可知，在風-震耦合作用下，當場地為軟土、硬黏土和巖土時塔頂側向位移最大值分別為0.360 m、0.409 m和0.337 m。由圖9(b)可知，在額定風速和極限風速下塔頂側向位移最大值分別為0.098 4 m和0.245 m。由圖9(c)可知，地震強度為8度時，當場地為軟土、硬黏土和巖土時塔頂側向位移最大值分別為0.368 m、0.344 m和0.310 m，場地為軟土時塔頂側向位移最大，場地為巖土時能量耗散速率和塔頂側向位移減小速度較慢。對比圖9(b)和圖9(c)可知，地震對塔頂側向位移的影響很大，與無地震時相比，在額定風速下發生地震時軟土、硬黏土和巖土塔頂側向位移最大值分別增大265%、316%和242%，在極限風速下分別增大47%、67%和38%。

圖10為不同工況下風力機塔基彎矩的變化。由圖10可知，在風-震耦合作用及不同土質的情況下塔基彎矩曲線的變化規律比較復雜。風力機在額定風速下氣動載荷最大。在極限風速下葉輪變槳導致氣動載荷減小，故塔基彎矩(最大值為66.3 MN·m)小于額定風速下的塔基彎矩(最大值為87.4 MN·m)。當場地為不同土質時塔基彎矩的最大值基本相同，均在65 MN·m左右。地震結束后(>450 s)，場地為巖土時能量耗散速率最慢，塔基彎矩降低速度也最慢。對比圖10(b)和圖10(c)可知，地震載荷對塔基彎矩的影響與氣動載荷相當，處于同一數量級。

地震加速度轉化為地震載荷作用于平臺底部，使其產生一定的加速度，場地為不同土質時平臺加速度如圖11所示。由圖11可知，地震載荷對平臺加速度的影響很大。無地震時，即在額定風速下平臺加速度始終為0 m·s-2，即平臺僅受地震載荷的影響。由于軟土阻尼較小，平臺自由度相對較大，在相同的地震激勵下平臺的動力響應更為劇烈。

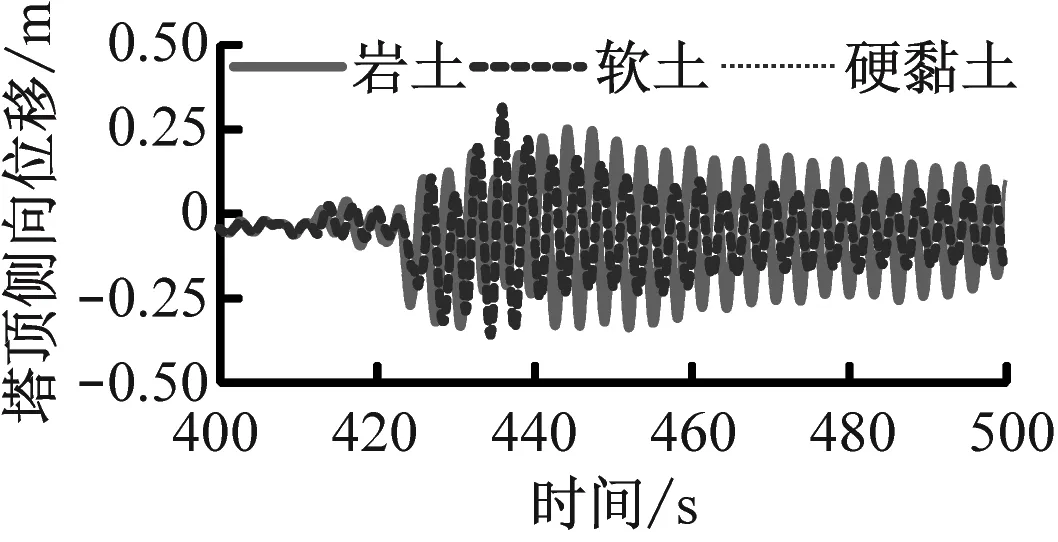
(a) 風-震耦合作用

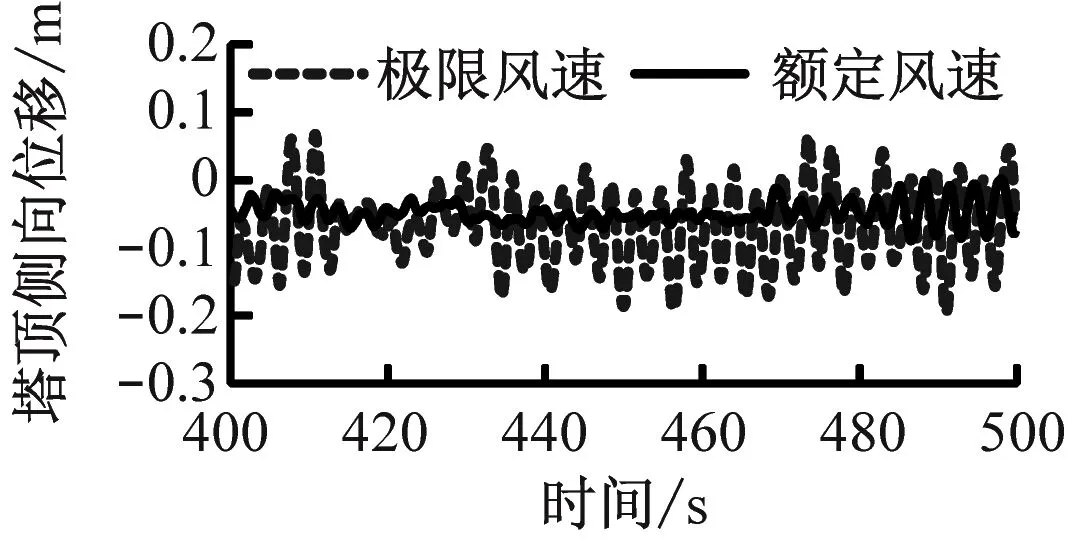
(b) 風單獨作用

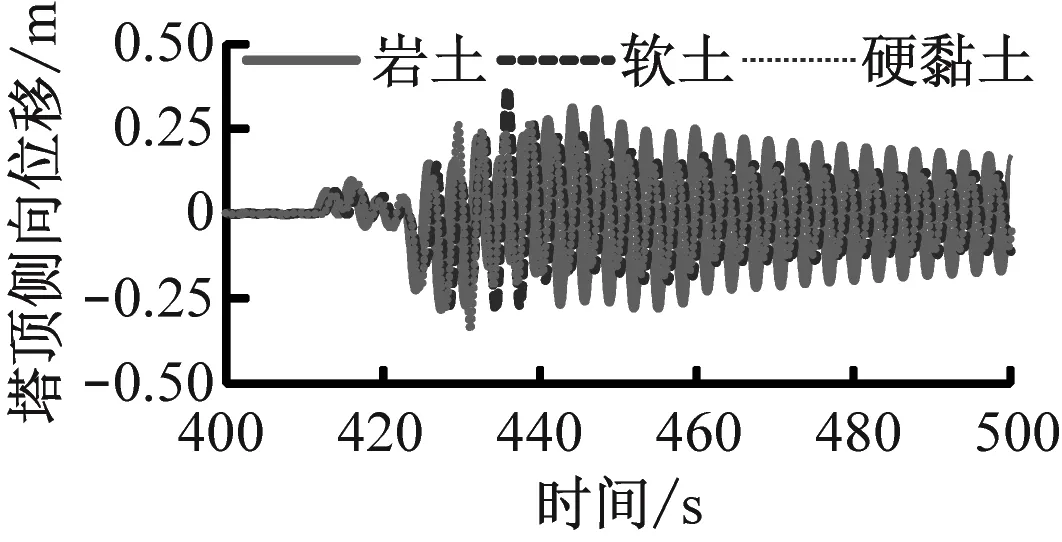
(c) 地震單獨作用圖9 不同工況下塔頂側向位移的變化Fig.9 Time domain variation of lateral displacement of tower top under different working conditions

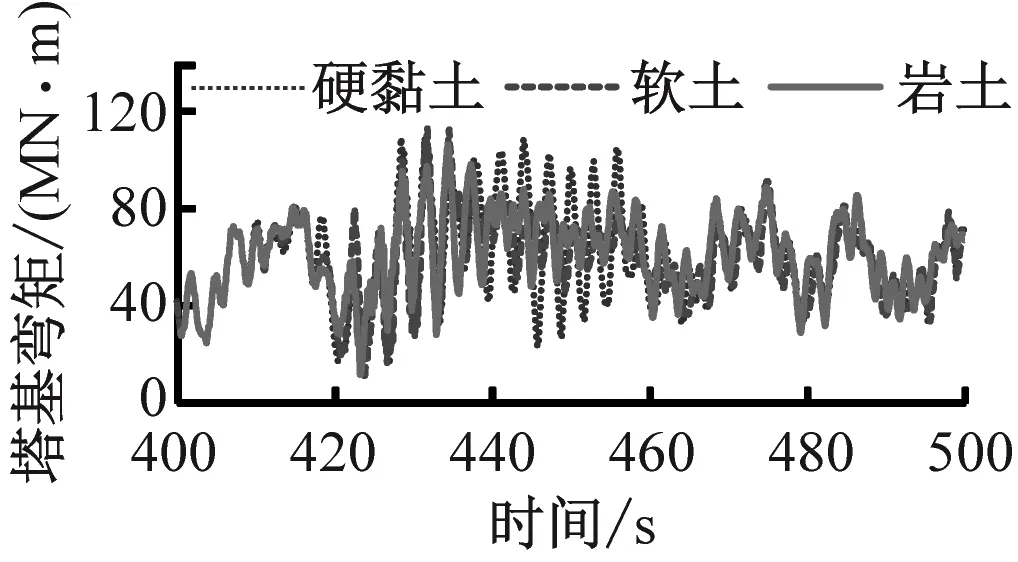
(a) 風-震耦合作用

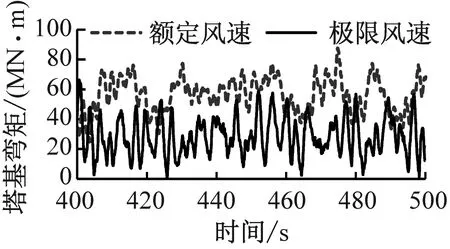
(b) 風單獨作用

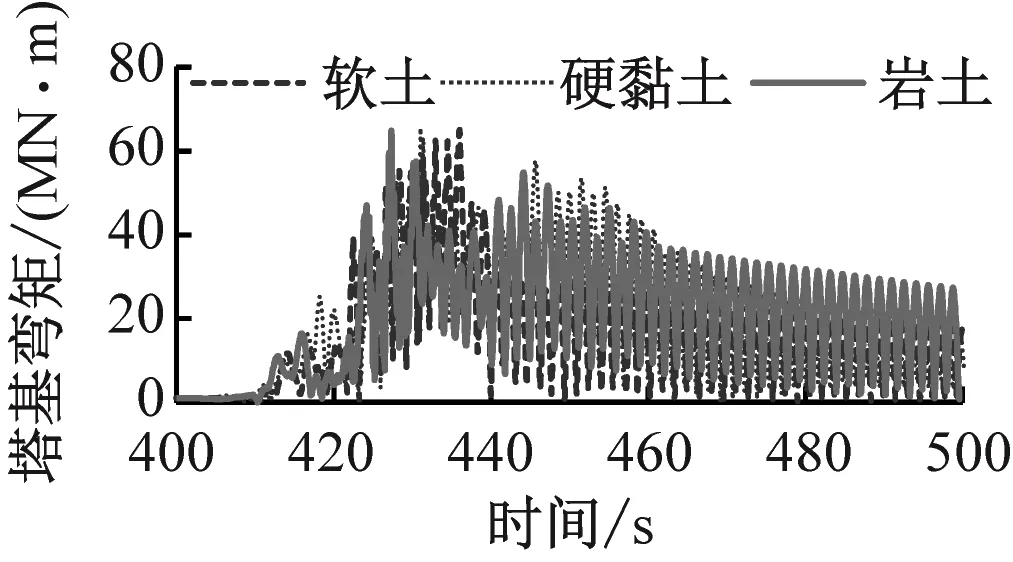
(c) 地震單獨作用圖10 不同工況下塔基彎矩的變化Fig.10 Time domain variation of bending moment of tower base under different working conditions

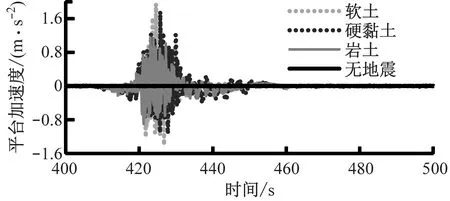
(a) 平臺前后加速度

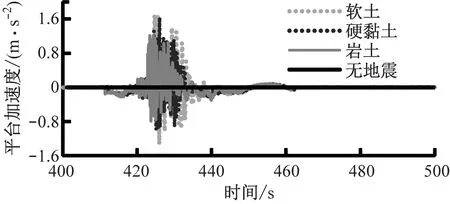
(b) 平臺側向加速度圖11 不同土質時風力機平臺加速度的變化

Fig.11 Time domain variation of platform acceleration for the tower in different soils

3.2 頻域分析

由于塔頂響應是風載荷、地震載荷等隨機載荷共同作用的結果，需通過頻域分析進一步研究塔架的振動特性。通過對400～500 s內塔頂的響應進行快速傅里葉變換(FFT)，對應的塔頂位移頻域動力響應如圖12所示。

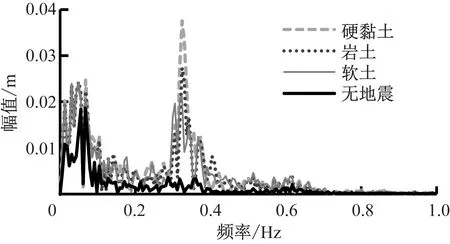
(a) 塔頂前后位移

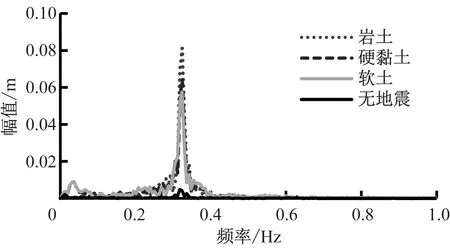
(b) 塔頂側向位移圖12 塔頂位移頻域動力響應

Fig.12 Dynamic response of tower top displacement in frequency domain

由圖12可以看出，無地震時塔頂振動尤其是塔頂側向振動不明顯。地震發生后，地震載荷使得塔架一階固有頻率(0.32 Hz)處的振動急劇增大。由此可知，地震是導致塔頂振動的主要因素，尤其是對塔頂側向振動的影響遠大于氣動載荷的影響。

4 結 論

(1) 在額定風速下，設防烈度為8度時，地震載荷對塔頂位移和塔基彎矩的影響不可忽視，尤其是對塔頂側向位移的影響遠大于氣動載荷；在極限風速下，地震載荷對塔頂側向位移的影響略大于氣動載荷。

(2) 地震載荷極大加劇了塔頂尤其是塔架一階固有頻率處的振動。設防烈度為8度時，塔頂振動主要激勵為地震載荷，氣動載荷對塔頂側向振動的影響較小。進行塔架結構抗震設計時，應充分考慮地震載荷的影響。

(3) 當場地為不同土質時，由于阻尼不同，塔架自由度及能量耗散速率不同，塔架時頻特性差異性較大。在風-震耦合工況下，與軟土和巖土相比，場地為硬黏土時塔架響應幅值和振動更大，故場地為硬黏土時風力機的結構抗震設計更應考慮SSI的影響。