教學細節給高效課堂添彩
——談數學教學中容易被忽視的細節

浙江省溫嶺市九龍學校 朱如燕

數學是一門特殊性的學科，它的特殊性表現在它既要研究如何以某種方式實現關于“數的分解的邏輯性”和“圖的組合的形象性”的優化過程，同時又要研究如何挖掘其中潛在的數學教學思想。如何讓學生在枯燥繁雜的數學學習中能更好地發展？在數學學習中可以利用一些教學中的細節對學生進行潛移默化的熏陶，讓學生能更好地發展。筆者在長期的教學實踐中是這樣做的：

一、板書設計的思想性

板書在數學課堂教學中起著舉足輕重的作用，好的板書能有效地啟發學生思考，高效地完成教學任務。筆者認為板書的作用不僅限于“發展智力”，還要試圖滲透給學生某種思想觀念，使其在智力發展的同時，也受到潛移默化的思想教育。這里的思想教育包括兩個方面：一是數學思想方法的教育，二是思想情感的教育。大部分教師忽略了這一點，認為數學知識上下章節之間銜接起來即可，豈不知這就失去了“啟發思維、發展智力”的最重要的因素——情感的投入。

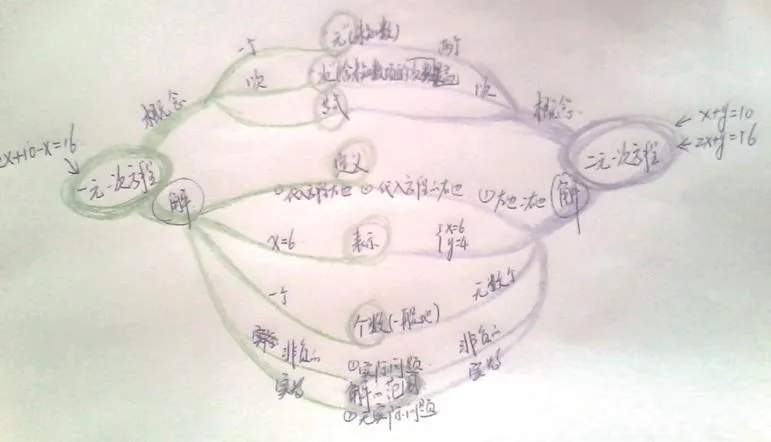
【案例】學生在了解一元一次方程知識本質的前提下，就能輕易類比二元一次方程的相關知識。同時，在課堂教學中，為了更好地揭示知識本質的類比，所以選用思維導圖進行板演，在知識層面，讓學生的思路清晰，讓知識的對比度更高；在情感層面，對相近知識要會聯系、會對比、會類比。

如果教師重視了這一點，并將其板書下來，教學行為方算完美，其板書設計才有可能真正達到“完成教學任務”的目的。

二、語言表達的抒情性

贊可夫在《和教師的談話》中說：“教師本身要具備這種品質——能夠領會和體驗生活中和藝術中的美，才能在學生身上培養出這種品質。如果照著教學法指示辦事，做得冷冰冰、干巴巴的，缺乏激昂的熱情，那是未必會有什么效果的。”相對而言，數學語言偏于理性，但是，倘若教者在進行嚴肅的邏輯推理和形象思維的過程中有“激昂熱情”的參與，會給這種純“理性”的認識添上一味“精神的”催化劑。如我們在引導學生認識圓周率“π”的意義時，如果“照著教學法指示辦事”，那么其小數點后幾位或十幾位數的記憶無非“點到為止”，其余就讓學生“強識”了，很明顯這樣做的效果自然滯后。但教者如果先以敬佩的眼光，滿懷激情地向學生講述一下關于“祖沖之如何推算圓周率”的小故事，那么學生的興趣會油然而生，情緒激昂起來，其效果定會事半功倍。

【案例】三國時期劉徽 “用圓內接正多邊形的周長來逼近圓周長”，劉徽計算到圓內接96邊形， 求得π=3.14，并指出內接正多邊形的邊數越多，所求得的π值越精確。而祖沖之在劉徽的基礎上，經過刻苦鉆研，反復演算，求出π在3.1415926與3.1415927之間，并得出了π分數形式的近似值，取為約率 ，取為密率，它是分子分母在1000以內最接近π值的分數。祖沖之究竟用什么方法得出這一結果，現在無從考查，若設想他按劉徽的“割圓術”方法去求的話，就要計算到圓內接16384邊形，這需要花費多少時間和付出多么巨大的勞動啊！由此可見，他在治學上的頑強毅力和聰敏才智是令人欽佩的。祖沖之計算得出的密率，外國數學家獲得同樣的結果已是一千多年以后的事了。為了紀念祖沖之的杰出貢獻，有些外國數學史家建議把π叫作“祖率”。

通過這個例子，學生就會提高學習積極性和學習的品質，讓學習內化為學生自身的需求，這樣就會讓學生從要我學變為我要學，效果就會大大提高。

三、作業設計的差異性

毋庸諱言，起鞏固強化知識作用的練習作業，大部分情況下，教師持一碗水端平的態度布置，這恰恰違背了“因材施教”的原則，無疑讓備受冷落的后進生雪上加霜，極大地壓抑了他們的心理。

客觀存在的差異，教者應以客觀的標準來對待。長有長的追求，短有短的目標，設計作業的“雷同”多會造成“撐死”和“餓死”兩極化的結果。難怪有的教師總戲謔為“利”不從心。如果教師善于運用心理學知識，追究產生落后生這一現象的根源，尋求轉化落后生的規律，那么其結果也許會變成“事遂心愿”。筆者根據班級學生實際，將班級分組并分別布置相應的作業，一部分名之曰“進步組”，作業以“識記”和“理解”為主，一部分名之曰“奮發組”，以“理解”和“應用”為主。顧名思義，學生在心理上首先產生一種相應的感知，驅動內心感化，促其動力外顯。一階段實施后，“進步組”的學生進步明顯，“奮發組”的學生對難題的學習、思考勁頭更足了。

【案例】如圖，直線a∥b，c∥d，求證∠1=∠3。

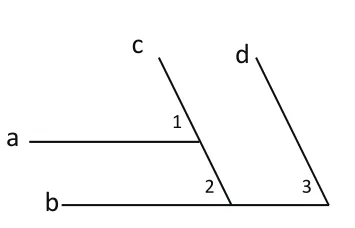
進步組：（1）在數量上∠1=∠3，

（2）在位置上∠1與∠3是同位角？

奮發組：（3）∠1與∠3有什么關系。

理由：（1）∵a∥b，∴∠1=∠2。

∵c∥d，∴∠2=∠3。∴∠1=∠3。

（2）∵∠1與∠2是同位角，∠2與∠3是同位角，∴∠1與∠3是同位角。

對于進步組的學生，教師要明確設置做題的方向，讓學生能明確知道解題的方法，這樣就能很好地達到鞏固知識的目標。

對于奮發組的學生，教師對于求解的題目就不需要很好的細化，讓學生在解題中根據解決問題的需要收集有用的信息，進行歸納，類比做出推斷，學生就會從角的數量關系、位置關系去考慮解決。奮發組的學生能將學到的知識運用起來，能很好地發散思維、展開想象、活學活用。 這一學習品質在分層作業教學中就很好地培養了。

教師要及時引導學生進行解題后的思考：（1）“查”：你能檢查這個結論嗎？能檢查這個論證嗎？你能給出幾種檢查？（2）“變”：我們應當不依常規，尋求變化，即以原題為中心進行發散，變解、變條件、變結論等。（3）“想”：做題之后常反思，我是怎樣想出來的？為什么這樣想？這道題的結論有什么用？經過一系列的反思，讓學生了解題目編寫的特點，在對比中學會反思、學會解題，同時讓學生的數學品質得到鞏固和提高。

四、教學思想的民主性

“集思廣益”一詞，人人都能“言”之有“理”，但并非人人都能真正訴諸行動，數學教學中就似乎缺少這種“行動”。“益”無非是“好處”，教師提出某個問題，大家紛說解決的方法，一比較就有了一種“最科學”的思路。但筆者認為這僅僅是對“民主性”的一個片面的理解——正面的理解。試想能解決問題，尤其能“科學”地解決問題的學生有多少？這就引出了容易使執教者忽略的另一個問題：那就是教師提出某個問題，大家紛說解決的方法，一比較就有了一種“最不科學”的思路。“最不科學”的那種思路多由落后生提出，教者如果熱處理，必然一棒將其打死，還談什么“轉化”。面對這些由落后生“集思”起來的“誤解”，引導學生真正懂得錯誤所在，就能更好地理解真理。

【案例】在學完冪的運算后，在單元測試中有這樣一道題：請你分析判斷：10010和10100這兩個數的大小。

首先讓答案是小于的學生解答：“這兩個數太大，但我可以用其他數來驗證：210與102，即1024與100，∵1024＞100，∴210＞102，通過以上驗證我發現了，如果指數與底數互換，原來底數小的冪就大，底數大的冪就小。∴10010＜10100。”我問：你只舉出一個例子，就能下結論了？他說：我在草稿上驗證了好幾個，都成立的。

原因分析：這是學生學會了教師所教給的“不進則退”的思想方法，利用不完全歸納法得到的。學生在前面學的一些運算律，都是根據不完全歸納法得出的。如加法交換律是這樣得出來的，“我們以前學過的加法交換律，在有理數的加法中它們還適用嗎？計算：30+（-20），（-20）+30，兩次所得的和相同嗎？換幾個加數再試一試。”就得出了加法交換律。

思考：剛進初中的學生能利用不完全歸納法驗證數學問題，是可佩的。教師如果就上面的解答打個“錯”，這無疑會損傷學生將來思考問題的積極性。

接下來對這個問題讓答案是大于的學生回答：先從比較12和21開始，發現后者大。但是24和42大小相等，再比較35和53，前者大。在學生的相互討論和陳述的過程中，學生就能很好地發現問題，并在能很好地調整方向，那么錯誤的解題就是一個雷區，讓其他學生能意識到運用不完全歸納法時不注意范圍的話就不一定都是正確的，任何時候恰當地分類是很有必要的。這樣做才能讓學生保持和增強學習數學的動力，才能有對數學強烈鉆研的欲望。

也許我們能真正體驗到“逆向思維”是“創造性思維”的一種特殊形式，從而認識到“誤解”同樣是有“益”的，讓“失敗”真正成為“成功”之母。

五、教學節奏的舒緩性

數學課的課堂結構是斜面的臺階式，思維就“度”而言漸強，由認知或補償練習到較易理解的例題，再到較難理解的例題，最后到綜合應用題，教學內容由淺入深，思維由一般到特殊，整個過程呈現一種小階梯大容量的局勢，使學生的思維一直處于緊張狀態。而執教者往往以帶領學生大踏步登上這個“臺階”為達到目的為樂，緊鑼密鼓，不敢松懈。事實上，這樣做固然能使學生登上“臺階”，但也難免氣喘吁吁，無暇體味登臺階的樂趣。

有經驗的教師往往在登一個臺階后讓學生思維稍微松弛一下，即講解例題或練習間隙適時調節學生的緊張情緒，如幽默半分鐘，一句話格言、與教學有關的奇人軼聞等等。俗話說“文武之道，一張一弛”。這樣做的效果要比“講、練、再講、再練”的高強度思維好得多。

總之，教育無小事，作為基礎學科的數學教育對于學生而言是枯燥的、抽象的，同樣也是重要的，除了學習“數的分解的邏輯性”和“圖的組合的形象性”以及潛在的數學思想方法，教師還應該在教學中注意“板書設計的思想性、語言表達的抒情性、作業設計的差異性、教學思想的民主性、教學節奏的舒緩性”，在教學中關注這五個細節，在細節中提升學生學習的品質，提高學生學習興趣，為我們高效的數學課堂添磚加瓦，給我們高效的數學課堂添彩，讓學生在課堂中能更高效、更出彩！