雷達輻射源信號識別特征參數集的構建方法

劉 飛, 何明浩, 韓 俊

(1.空軍預警學院, 湖北 武漢 430019; 2. 中國人民解放軍95174部隊, 湖北 武漢 430040)

0 引 言

隨著數據采集、存儲、傳輸技術的快速發展,雷達輻射源信號(radar emitter signal,RES)識別方法逐漸從傳統的信號脈沖描述字轉向了基于脈沖波形數據的脈內特征參數[1-2]。因此,挖掘和提取更能表征RES的脈內特征參數成為研究熱點,如:頻譜特征[3-4]、時頻特征[5-9]、雙譜特征[10]、模糊函數特征[11-12]、相像系數特征[13]、熵特征[14-17]、復雜度特征[18]等出現在各文獻研究中。各種脈內特征參數的挖掘應用一定程度上解決了傳統識別方法中的錯分誤判問題,提高了雷達輻射源識別的準確率。

然而,脈內特征參數在工程應用中的一些局限性也慢慢涌現出來[19-20]。一個常見的局限性就是大多特征僅對限定調制類型的RES具有較好的識別性能,而難以識別其他調制類型的RES[21-22]。例如,時頻特征對單載頻信號、線性調頻信號、非線性調頻信號有很好的識別效果,但對頻率編碼信號和頻率分集信號卻無能為力;再如,模糊函數特征對頻率編碼信號和頻率分集信號有很好的識別效果,但對非線性調頻信號和線性調頻加二相編碼信號的識別率卻并不高。另一個局限性是單個特征的識別率隨仿真條件的變優而有趨于“邊緣效應”的現象,不能突破自身識別率的“瓶頸”[23-24]。在特征提取仿真試驗中,當特征維數達到一定值后,增加特征維數并沒有帶來明顯的識別率收益,相反,提取較高維數的特征會顯著提高識別時間成本。

針對上述問題,本文擬通過組合不同種類的特征,構建特征參數集,集聚各特征參數在不同調制類型RES中的識別優勢,提升基于特征參數集的識別方法的通用性和準確性。

1 特征組合及性能分析

特征組合是指將兩種及以上不同特征參數,通過特征數據的連接,變為一種新的特征的過程。給定兩種分別為m維和n維的特征，即A={a1,a2,…,am}和B={b1,b2,…,bn},則他們可以按以下方式組合，即

[A,B]={a1,a2,…,am,b1,b2,…,bn}

(1)

或:

[B,A]={b1,b2,…,bn,a1,a2,…,am}

(2)

上面2種組合方式,僅是2種特征參數特征數據連接順序的不同。由式可知,特征組合后的維數為2種對應特征的維數之和,即A和B的特征組合維數為m+n。

1.1 特征種類對識別性能的影響

討論不同類型的特征參數組合對識別性能的影響。對引言中提及的7種特征進行仿真分析,仿真條件為:訓練數據的樣本量為3 500(每種特征500個),測試數據的樣本量為700(每種特征100個),分類器為支持向量機(support vector machine,SVM),SVM核函數為徑向基函數(radial basis function,RBF),RBF參數γ=0.200 0,懲罰系數C=0.100 0。

分別以每種特征為對象,與其他特征進行組合,特征組合性能仿真結果如圖1所示,圖1中,橫坐標“1”至“6”分別代表其他特征,次序與頻譜特征、時頻特征、雙譜特征、模糊函數特征、相像系數特征、熵值特征、復雜度特征一致。

圖1 各種特征與其他特征組合識別性能Fig.1 Recognition performance of various characteristics combined with other characteristics

由圖可知,特征組合對識別性能的影響有以下3種情況:

(1) 組合特征識別率同時高于對象特征和其他特征,如雙譜特征、模糊函數特征、相像系數特征,說明此類特征與其他特征的組合對雙方均是有益的,屬于互利型特征;

(2) 組合特征識別率高于對象特征而部分低于其他特征,如時頻特征、復雜度特征,說明此類特征與其他特征的組合對自身是有益的,而對其他特征并不一定有益,屬于利己型特征;

(3) 組合特征識別率高于其他特征而部分低于對象特征,如頻譜特征、熵值特征,說明此類特征與其他特征的組合對其他特征是有益的,而對自身并不一定有益,屬于利它型特征。

總體來說,組合特征的識別性能與單個特征相比是提升的,在仿真中沒有出現組合特征識別率同時低于對象特征和其他特征的情況。

1.2 組合順序對識別性能的影響

討論特征分別按照式(1)與式(2)進行組合對識別性能的影響。將7種特征按頻譜特征、時頻特征、雙譜特征、模糊函數特征、相像系數特征、熵值特征、復雜度特征的次序兩兩進行組合,由此得到的特征組合稱為順序組合;將上述組合的次序進行交換,由此得到的特征組合稱為反序組合。在第1.1節的仿真條件下,各特征組合的順序和反序識別率如圖2所示。

圖2 特征組合順序對識別性能的影響Fig.2 Effect of characteristic combination order on recognition performance

由圖2可知,各特征組合的反序識別率與順序識別率完全一致,說明特征組合排列次序的改變對識別性能是沒有影響的。通過對其他特征組合方式的仿真驗證,均有此結論。因此,特征組合式(1)和式(2)是等效的。

1.3 特征個數對識別性能的影響

討論不同個數的特征參數組合對識別性能的影響。為討論問題的完備性,將單個特征作為特征個數為1的情況納入對比分析。根據特征組合公式,對于N種不同類型的特征參數,特征組合方式的總數為

(3)

在對7種特征所有組合方式的性能分析中發現,特征組合可分為2種情況:

(1)優型組合,如i=2、i=3、i=5時,識別率排名第1的組合方式等,他們的識別率高于對應特征的其他所有組合情況,定義該類組合為優型組合。優型組合實現了特征參數識別率的提高,是在進行組合時最希望得到的結果。

以i=5中排名第一的組合為例,其對應特征為時頻特征、雙譜特征、模糊函數特征、相像系數特征、熵值特征,對應特征的其他所有組合與該組合的識別率對比情況如圖3所示,圖3中橫坐標為其他組合序號,虛線為該組合識別率參考線98.43%。

圖3 優型組合示例圖Fig.3 Example diagram of optimal combination

由圖3可知,其他組合的識別率均低于該組合識別率,圖3中接近虛線的3個識別率分別為98.29%、98.14%、98.29%,故該組合為優型組合。

(2)非優型組合,如i=2至i=7時,識別率排名倒數第一的組合方式等,他們的識別率低于對應特征的所有組合中的部分組合情況,定義該類組合為非優型組合。非優型組合并沒有實現相對所有特征參數識別率的提高,所以在實際應用中往往舍棄這類組合。

以i=5中排名倒數第1的組合為例,其對應特征為頻譜特征、時頻特征、雙譜特征、模糊函數特征、復雜度特征,對應特征的其他所有組合與該組合的識別率對比情況如圖4所示,圖4中橫坐標為其他組合序號,虛線為該組合識別率參考線77.57%。

圖4 非優型組合示例圖Fig.4 Example diagram of non-optimal combination

由圖4可知,其他組合的識別率有低于該組合識別率的情況,也有高于該組合識別率的情況,故該類組合為非優型組合。

2 特征參數集構建規則

特征參數集是特征組合(含單特征)中優型組合的一種,若記某特征參數集為Θ,所有特征參數組合構成的集合為Ω,則{Θ}為Ω的一個子集,即:{Θ}?Ω。所有特征參數集構成的集合Ψ,Ψ是對Ω的精簡,即:Ψ?Ω,在識別率上Ψ和Ω是等效完備的。

根據第1.3節對優型組合的定義,優型組合的識別率高于對應特征的其他所有組合情況,同樣,特征參數集的識別率應高于組成參數集對應特征的其他所有組合情況。設某特征參數集Θ={Θ1,Θ2,…,Θn},由對應特征Θ1、Θ2、…、Θn的其他組合構成的集合記為Λ,由Θ1、Θ2、…、Θn組成的特征參數集全集記為Ψ,則關于特征參數集Θ有以下結論成立:

(1)Θ的識別率高于Λ中所有元素的識別率，即

p(Θ)>p(κ|Λ)

(4)

式中,p(·)為識別率函數,κ為Λ中的元素。

(2)Θ為Ψ中含特征參數個數最多的集合,當θ為全特征參數集時,與Λ互為補集，即

(5)

式中,Φ為空集。

(3) 當Θ為單特征參數集時,{Θ}=Ψ,Λ=Φ。

(4) 所有單特征構成的組合{Θ1},{Θ2},…,均為特征參數集。

(5) 對于特征個數分別為n、n+1的特征參數集Θn和Θn+1,若滿足Θn?Θn+1,則稱Θn和Θn+1為同源特征參數集。同源特征參數集的最大識別率是隨特征個數遞增的,即

max(p(Θn+1(Θ1,Θ2,…,Θn)))>

max(p(Θn(Θ1,Θ2,…,Θn)))

(6)

因此,對于從特征參數組合中找出所有的特征參數集,可根據其構建規則,按特征個數遞增的步驟進行標記。

步驟1標記所有單特征組合為特征參數集;

步驟2對所有的兩個特征組合,與對應的單特征組合進行比較,若某組合識別率均高于單特征,則標記該組合為特征參數集;

步驟3對所有的3個特征組合,與步驟1、步驟2中對應的特征參數集進行比較,若某組合識別率均高于已標記的對應特征參數集,則標記該組合為特征參數集;

步驟4后續個數的特征組合,可類似步驟3,與之前所有已標記的對應特征參數集進行比較,依次標記是否為特征參數集。

3 特征參數集時間成本分析

對于同源特征參數集,特征個數越多識別率越高,然而,高的識別率有可能耗費較高的時間成本。在RES識別中,由于SVM屬于基于統計學習的分類器[25-28],其分類模型可提前通過學習訓練獲得,因此,參數集的時間成本主要由識別過程的2個環節產生,一是特征提取環節產生的特征提取時間,另一是分類識別環節產生的分類識別時間。

計算算法時間的常用方法有2種,一種是計算該算法中所有語句的頻度之和[29],另一種是計算算法執行時用到的加減乘除等運算的次數[30-31]。這2種方法通過對算法的詳細分析均能準確地定量計算出算法的時間,但是,隨著算法開發平臺和對應計算機語言的發展,大量使用各種算法包和隱性封裝各種函數,使準確分析出算法的步驟變得十分困難。因此,本文采用工程應用中常用到的統計分析方法,來獲取特征提取時間和分類識別時間。

3.1 特征提取時間

由于特征參數的提取時間和原始波形數據的長度有關,而原始波形數據的長度與信號采樣率和脈沖寬度有關,對于未知信號,信號的脈沖寬度是不能事先獲得的,所以,原始波形數據的長度也無法事先確定。但是,為便于統一決策參考,這里將原始波形數據的基準長度定義為2 048(采樣頻率為120 MHz時,脈寬范圍為8.54～17.06 μs)。

分別根據特征提取算法,對隨機產生的不同調制類型的原始波形數據做特征提取實驗,記錄每次實驗耗費時間,如此進行200次蒙特卡羅實驗,將實驗時間均值作為特征提取時間。表1所示為各特征參數的提取時間,實驗平臺參數為:英特爾i3雙核CPU,主頻1.70 GHz,內存4.00 GB,Windows 8.1中文版64位操作系統。

表1 特征參數提取時間

3.2 分類識別時間

SVM在進行RES識別時,分類識別時間主要與樣本的維數有關,在7種特征參數中,頻譜特征、時頻特征、雙譜特征、模糊函數特征的維數為256維,記為一次變換特征,相像系數特征、熵值特征、復雜度特征的維數為2維,記為二次變換特征。由于一次變換特征與二次變化特征在維數上相差較大,多次仿真實驗表明,當一次變換特征與二次變換特征組合時,二次變換特征的維數對分類識別時間的影響較小。0～4個一次變換特征及其分別與1～3個二次變換特征組合的分類識別時間如圖5所示,圖5中橫坐標依次為1個二次變換特征的組合、2個二次變換特征的組合、3個二次變換特征的組合、1個一次變換特征的組合、1個一次變化特征與1個二次變換特征的組合、1個一次變化特征與2個二次變換特征的組合、……、2個一次變換特征的組合、2個一次變化特征與1個二次變換特征的組合、……、4個一次變化特征與3個二次變換特征的組合。

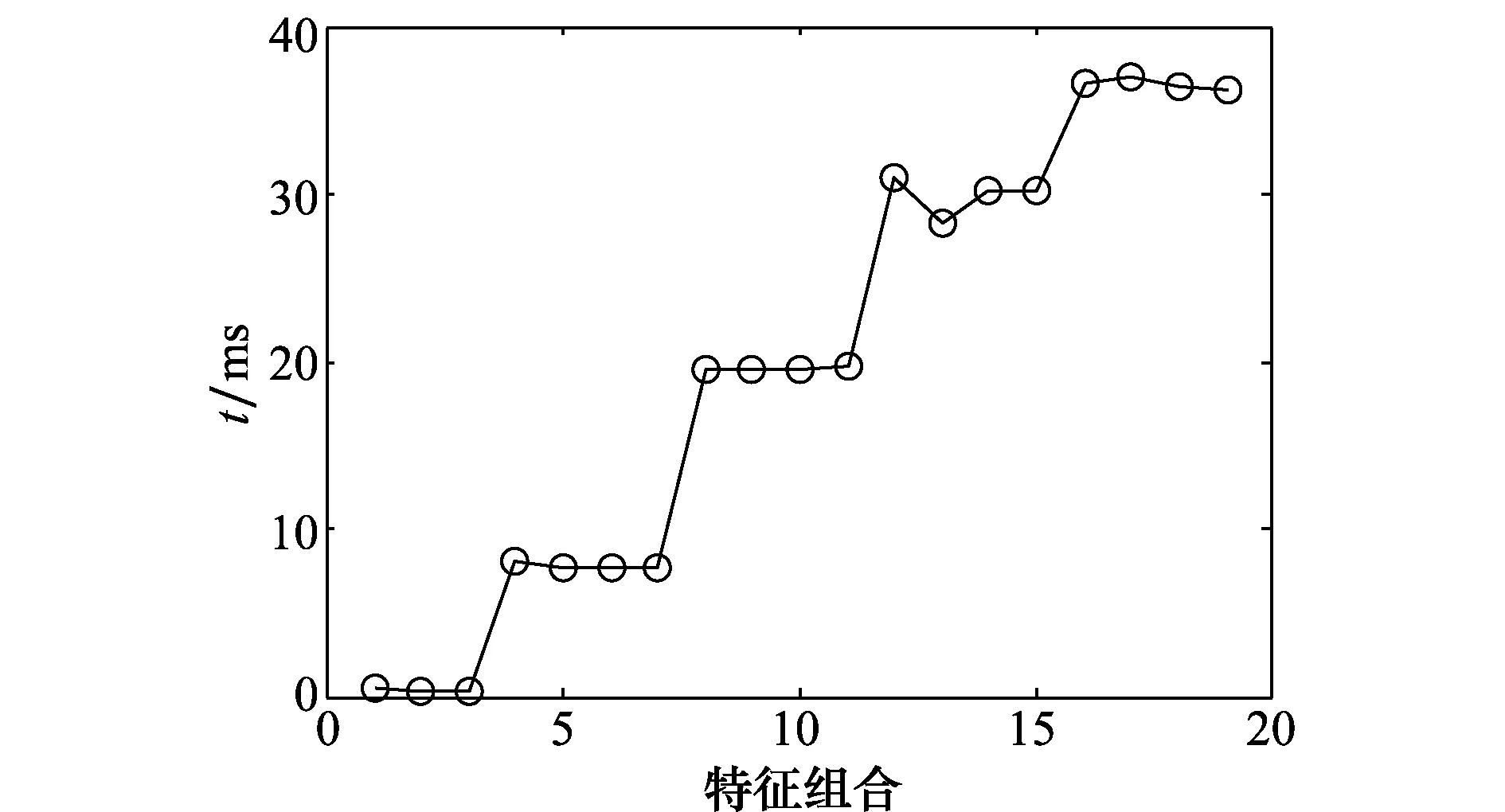
圖5 特征組合分類識別時間圖Fig.5 Time map of characteristic combination classification and recognition

由圖5可知,特征組合分類識別時間隨一次變換特征個數的增加呈階梯狀遞增,因此,按照一次變換特征的個數,可將分類識別時間分為5個等級,分別對應0～4個一次變換特征及其與二次變換特征組合方式。通過多次蒙特卡羅實驗,獲得不同等級的分類識別時間如表2所示(實驗平臺參數同上)。

表2 特征組合分類識別時間

3.3 總時間成本

在RES識別中,特征提取環節和分類識別環節之間為串聯關系。因此,特征參數集的總時間成本為特征提取時間和分類識別時間之和,即

T=Tc+Ts

(7)

式中,T為參數集的總時間成本；Tc為特征提取時間；Ts為分類識別時間。

(8)

若Θ={Θ1,Θ2,…,Θn}中屬于一次變換特征的個數為m,則參數集分類識別時間為

(9)

4 2種典型特征參數集的應用構建

根據上述特征參數集的構建規則和時間成本計算方法,得出7種特征的所有參數集的識別率和時間成本如表3所示,表中,fft、stft、bi、amb、cr、en、cp分別代表頻譜特征、時頻特征、雙譜特征、模糊函數特征、相像系數特征、熵值特征、復雜度特征。

表3 特征參數集的識別率和時間成本

各特征參數集的對應識別率和時間成本數據按式(10)進行歸一化。

(10)

式中,dmax、dmin分別為數據序列{d1,d2,…,dn}中的最大值和最小值。

歸一化后的特征參數集識別率與時間成本之間的關系如圖6所示。

由圖6可知,特征參數集的識別率和時間成本之間并沒有出現嚴格一致的變化關系,也就是說特征參數集特征組成情況與識別率、時間成本之間沒有恒定的單調關系,因此,需要根據實際需求做出最優的決策——在獲得較高識別率的同時消耗較小時間成本。

圖6 特征參數集識別率與時間成本對應關系Fig.6 Relationship between recognition rate and time cost of characteristics parameters

在RES識別中,有2種情況是經常遇見的,一是現場采集波形數據,實時識別RES;二是采集存儲波形數據,事后識別RES。對于第1種情況,最優決策是在限定識別率條件下,選擇時間成本最小的特征參數集,該特征參數集定義為時效集;對于第2種情況,最優決策是在限定時間成本條件下,選擇識別率最高的特征參數集,該特征參數集定義為精準集。

4.1 時效集

記特征參數集為Θ,所有特征參數集構成的集合為Ψ,則時效集為

ΘAE=

Θ|(Θ∈Ψ,min(T(Θ))|p(Θ)≥p0)

(11)

式中,T(Θ)為特征參數集的時間成本；p(Θ)為特征參數集的識別率；p0為限定識別率。

根據定義式(11),構建特征參數時效集的方法步驟如下:

步驟1將所有特征參數集的識別率表和時間成本表按特征參數集的構建方式進行對應合并整合;

步驟2找出所有識別率高于限定識別率的特征參數集;

步驟3找出步驟2中時間成本最小的特征參數集。

例如,某實時識別場合,給定最低識別率為85%,根據合并整合的特征參數集表(表3),篩選出特征參數集有序號1、4、8、9、10、……,上述特征參數集中,時間成本最小為10.58 ms,對應序號1,特征參數集構成為頻譜特征,此即為滿足需求的時效集。

4.2 精準集

記特征參數集為Θ,所有特征參數集構成的集合為Ψ,則精準集為

ΘCP=Θ|(Θ∈Ψ,max(p(Θ))|T(Θ)≤T0)

(12)

式中,p(Θ)為特征參數集的識別率；T(Θ)為特征參數集的時間成本；T0為限定時間成本。

根據定義式(12),構建特征參數精準集的方法步驟如下:

步驟1將所有特征參數集的識別率和時間成本按特征參數集的構成方式進行對應合并整合;

步驟2找出所有時間成本小于限定時間的特征參數集;

步驟3找出步驟2中識別率最高的特征參數集。

例如,某實時識別場合,給定最低每次識別時間在1 s以內,根據合并整合的特征參數集表(見表3),篩選出特征參數集有序號1、2、3、……、27、……,上述特征參數集中,識別率最高為95.86%,對應序號27,特征參數集構成為頻譜特征、模糊函數特征、復雜度特征,此即為滿足需求的精準集。

5 結 論

為突破單個脈內特征參數識別性能的“邊緣效應”,獲得更高的識別率,從特征參數的組合入手,提出特征組合的方式和相關約定,并重點研究了特征種類、特征個數、信號環境對特征組合識別性能的影響。在此基礎上,進一步對特征組合中的優型組合進行研究討論,提出特征參數集的構建規則和生成方法,并就特征參數集的時間成本進行了分析。最后,根據識別率和時間成本因素,構建了2種典型的特征參數集——時效集和精準集,為脈內特征參數集在RES監測、偵察、分析等工程應用方面奠定了良好的理論基礎。