階次跟蹤能量算子與奇異值分解結合的滾動軸承故障診斷

江志農，胡明輝，馮坤，賀雅

(北京化工大學 診斷與自愈工程研究中心，北京 100029)

振動分析是滾動軸承狀態監測的主要方法，軸承故障產生的振動信號通常是瞬態、非平穩的，并且受到高頻載波信號調制[1-2]，對其直接應用傳統的包絡解調容易產生“頻譜模糊”現象[3-4]，無法有效提取故障特征。能量算子能有效分析具有時變幅值和時變頻率特征的振蕩信號[5-7]，并且計算復雜性小，精度高；階次跟蹤方法[8]則可對時域上的非平穩信號進行等角度重采樣，從而得到角域上的準平穩信號。

同時，軸承故障初始階段引起的振動通常為微弱振動信號，其沖擊特征常湮沒于機械系統大量干擾源產生的背景噪聲中，提取故障特征時有必要對信號進行降噪處理。奇異值分解(Singular Value Decomposition，SVD)能夠對噪聲混雜信號中的有用部分進行有效、可靠地估計，且基于SVD的降噪方法計算量小，在信噪比較低的情況下仍然能夠分離有用信息與噪聲信號，特別適合軸承振動加速度信號的降噪[9-10]。

因此，針對滾動軸承變速運行過程中的時域振動信號，提出了將階次跟蹤能量算子與奇異值分解相結合的滾動軸承故障診斷方法，以有效提取滾動軸承的故障特征。

1 奇異值分解降噪

設A為實信號X通過變換所得到的m×n階實矩陣，其滿足

A=UΛVH，

(1)

式中：U，V分別為m×m，n×n階正交矩陣；Λ為m×n階對角矩陣，其所有的對角元素非負且降序排列，這些對角元素即為信號矩陣A的奇異值。實踐表明，所測信號的信噪比越大，矩陣Λ對角線上的零值元素數量越多。根據矩陣Λ對角線上零值元素的數量可近似估計出信號的信噪比。基于該理論發展而來的SVD降噪技術[11]為：首先，將矩陣Λ中奇異值很小的元素置零，構造一個新的矩陣Λ′；然后，根據(1)式重新計算得到實矩陣A′,并推導出降噪后的信號。

2 階次跟蹤能量算子

階次跟蹤能量算子(Order Tracking Energy Operator，OTEO)是能量算子(EO)在角域上的應用，是對EO的改進和完善，可用于變工況下滾動軸承的微弱故障特征提取。

2.1 階次跟蹤

階次的定義是旋轉機械軸每轉發生振動的次數。也就是說階次相對于轉速是無關的，故障頻率是轉頻的某一階成分。階次的定義為

(2)

式中：O為階次；n為軸的轉速，r/min；f為故障頻率，Hz。

階次分析的關鍵在于等角度采樣，實質上是等角度時刻的獲取，得到等角度采樣時刻后在原函數上插值擬合即可得到角域上的平穩信號[12]。

2.1.1 重采樣

采用多相FIR濾波器對振動信號原始波形進行重采樣，提高采樣頻率，防止在等角度采樣時發生頻率混疊[13]。

提高采樣頻率的重采樣相當于在原始信號上插值。如圖1所示，信號x(n)的采樣頻率提高L倍，得到v(n)，也即在x(n)每相鄰的2個點之間插入L-1個0，設計低通濾波器h(n)對v(n)進行低通濾波，從而得到插值后的輸出y(n)。

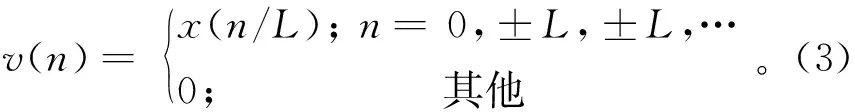
圖1 插值濾波流程圖Fig.1 Flow chart of interpolation filtering

2.1.2 獲得等角度序列

由轉速趨勢得到各采樣點對應旋轉過的角度，找出角度最小值及最大值，根據每轉上采樣點數是最大預分析階次的2倍生成等角度序列，即當轉軸經過這些等角度點時進行采樣[14]。

設原采樣間隔為Δt，第k個采樣點i轉速為vi，則對應的轉角為

(4)

則采樣點對應時刻ti=kΔt時的轉軸轉角為

(5)

得到t1-ti內等角度采樣點數為

(6)

式中：M為預分析最大階次，由等角度重采樣定理得每轉上采樣點數為2M，即角域的采樣頻率。根據采樣定理，M應滿足

(7)

式中：nmax為采樣時間內軸的最大轉速；fs為原始振動信號的采樣頻率。綜上可得等角度序列為

(8)

2.1.3 二次插值

插值是指已知2組數據之間的對應關系，得出關心的非采集得到的數據對應的變量值。在此采用分段線性插值方式，這種擬合方式認為2個樣本點之間符合一次函數(y=ax+b)的關系，將兩點直線連接起來，已知兩點之間的因/自變量就可以得到對應的變量。如圖2所示，各樣本點之間的時間間隔為Δt，在樣本點之間以等角度間隔Δθ插值，得到等角度采樣時標Tn。

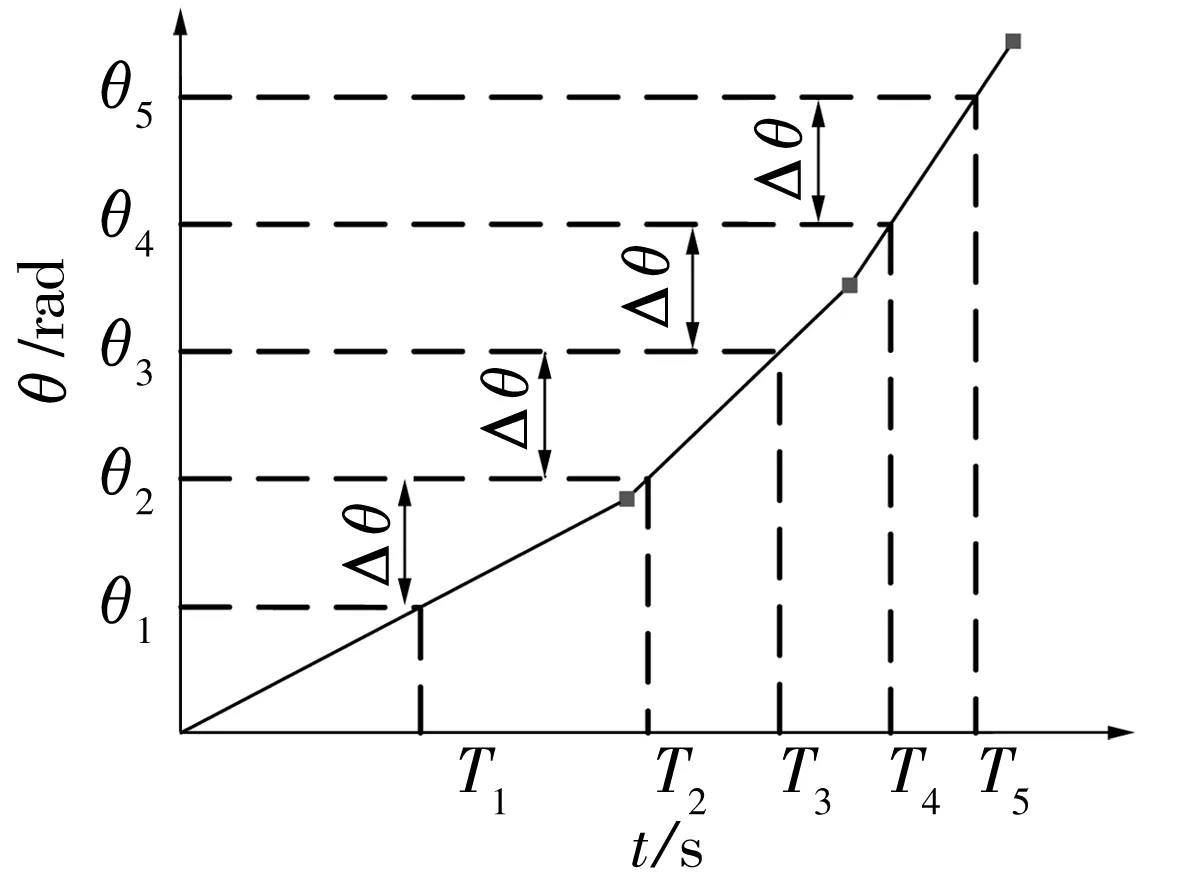
圖2 插值得到等角度采樣時間Fig.2 Equal angle sampling time after interpolation

在重采樣之后的振動信號上以等角度采樣時標插值擬合后，就得到了角域上的平穩信號，實現轉速無關化，按照轉速趨勢實現等角度重采樣的流程如圖3所示。

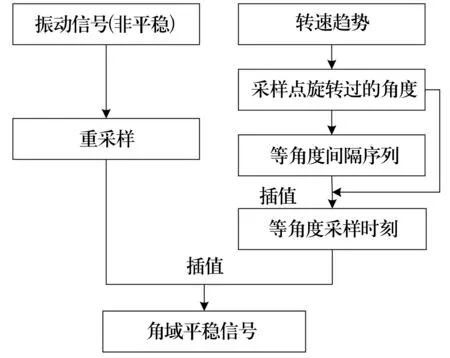
圖3 等角度重采樣流程圖Fig.3 Flow chart of equal angle resampling

2.2 階次跟蹤能量算子

對于調幅調頻信號x(t)，其能量算子定義為

(9)

則x(t)的振幅包絡信號為

(10)

通過能量算子的運算可求得加速度信號的振幅包絡信號，對包絡信號進行FFT分析即可得到包絡頻譜[15]。對于滾動軸承故障信號而言，包絡信號|a(t)|的頻率成分主要為軸承故障特征頻率fF及其諧波[16]，即|a(t)|是否平穩取決于fF是否為一個固定值。對于通常外圈固定、內圈旋轉的軸承，其不同元件的故障特征頻率可簡化為[17]

fF=anr，

( 11)

式中：a為常數；nr為軸承內圈轉速。由(11)式可知,軸承故障特征頻率與轉速成正比。在穩定工況下運行時，軸承故障特征頻率為一固定值，對|a(t)|做FFT分析即可提取出故障特征。而在變工況下運行時，軸承故障特征頻率隨轉速發生變化，直接對|a(t)|進行FFT分析會產生頻譜模糊現象。

為了消除轉速對特征頻率的影響，在FFT分析之前先對|a(t)|進行階次跟蹤處理，得到角度域的平穩信號|a(r)|，然后再進行FFT分析得到階次域包絡頻譜，該頻譜包含軸承故障特征且實現了與轉速的無關化。

綜上所述，針對變工況引起的能量算子解調信號非平穩問題，定義階次跟蹤能量算子，其實現步驟如下：

1)根據(10)式對變工況下時域振動信號進行基于EO的分析，得到包絡信號|a(t)|；

2)對時域非平穩信號|a(t)|進行階次跟蹤分析，得到角度域平穩信號|a(r)|，實現由非平穩信號向角度域上準平穩信號的轉換；

3)對|a(r)|進行FFT分析，得到階次域的包絡頻譜，解決由直接對非平穩信號進行FFT分析帶來的頻率模糊問題。

根據OTEO提取出的滾動軸承故障特征階次，在一定程度上解決了變工況造成的頻譜模糊問題，可實現變工況下滾動軸承的故障特征提取。

3 SVD與OTEO結合的診斷方法

階次跟蹤能量算子解決了滾動軸承故障特征提取中包絡及變工況引起的頻譜模糊問題,然而，工程中采集的軸承座加速度信號通常成分較復雜，直接對其進行包絡分析效果較差，需要在包絡分析之前進行降噪處理[18]。因此，提出將階次跟蹤能量算子與奇異值分解相結合的滾動軸承診斷方法，其流程如圖4所示。

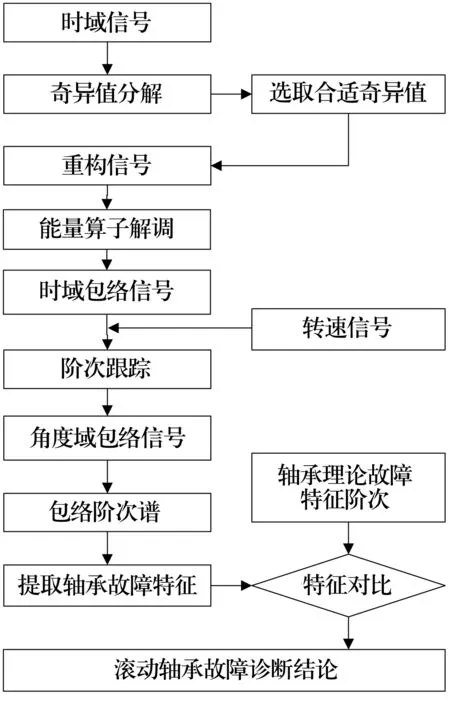
圖4 基于OTEO與SVD算法的流程圖Fig.4 Flow chart of algorithm based on OTEO and SVD

4 故障診斷實例

4.1 試驗介紹

軸承故障模擬試驗臺如圖5所示。試驗預置1#軸承(圓柱滾子軸承)為故障軸承，在其內圈滾道面加工一條寬、深均為1 mm的槽以模擬軸承內圈故障。由故障軸承基本參數(Dw=8 mm，Dpw=125 mm，Z=34)計算可得軸承內圈故障特征頻率對應階次為18.088。由于1#軸承缺乏與其直接連接的軸承座，振動響應需經過軸系傳遞到相鄰軸承(2#軸承)，再經過薄壁復雜路徑傳遞到測點位置。信號受傳遞路徑和工作環境影響，在傳遞過程中大量衰減并混入噪聲，在測點得到的軸承故障特征信號相對于噪聲極其微弱。

圖5 軸承故障模擬試驗臺Fig.5 Test rig for bearing fault simulation

數據采集設備為LMS SCADAS振動測試系統，加速度傳感器型號為BK 4519，鍵相傳感器為接近開關。在內圈轉速由737 r/min升至827 r/min的過程中(圖6)采用加速度傳感器和接近開關采集數據。變速過程中滾動軸承的故障信號時域波形如圖7所示(圖中g為重力加速度，取9.8 m/s2,下同)，從圖中可以看出，時域信號呈現出非平穩特征，應用傳統包絡解調方法容易產生如圖8所示的頻譜模糊現象。

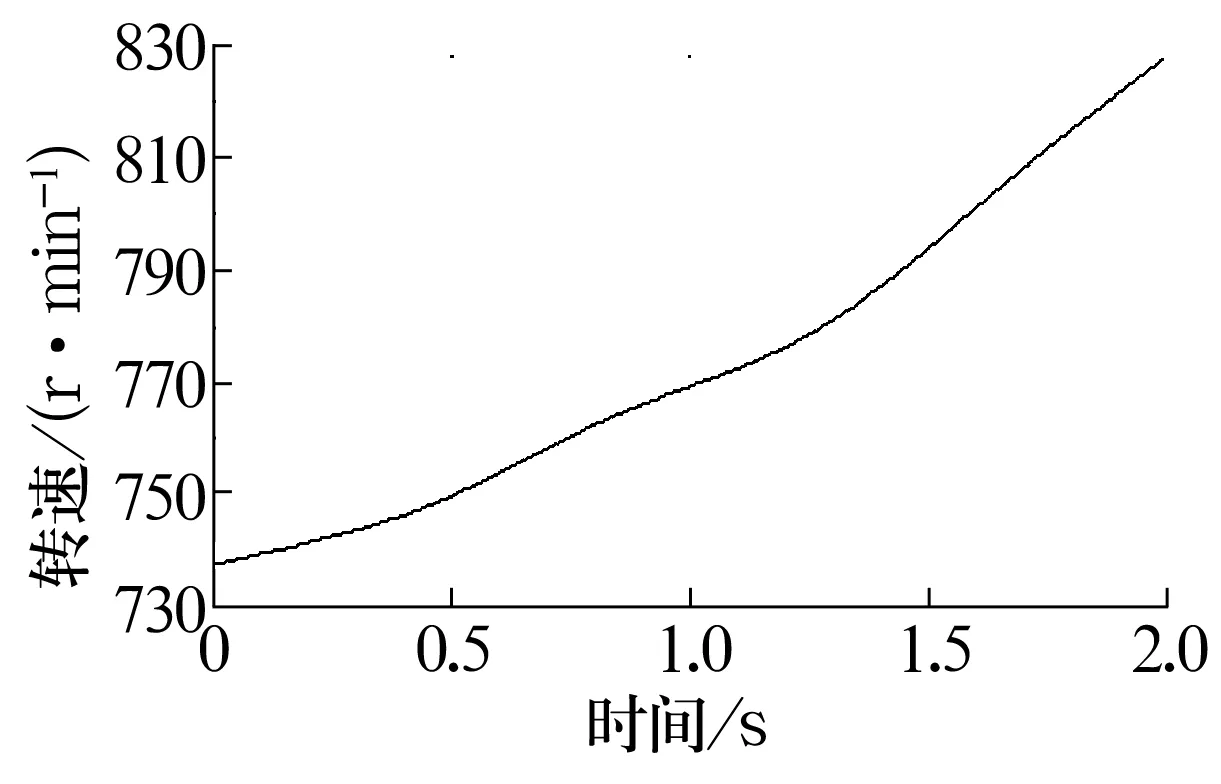
圖6 轉速趨勢Fig.6 Trend of rotational speed

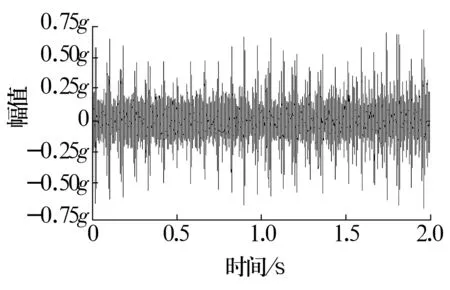
圖7 振動加速度信號波形Fig.7 Signal waveform of vibration acceleration

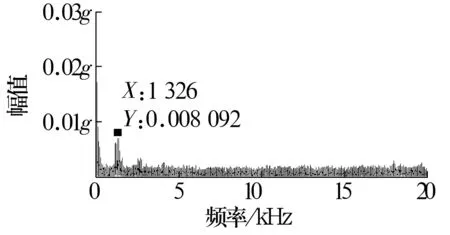
圖8 轉速變化引起的頻譜模糊現象Fig.8 Spectrum amgibuity phenomenon caused by varied rotational speed

4.2 OTEO與SVD結合的分析方法

首先，利用SVD對原始信號進行降噪，結果如圖9所示，從圖中可以看出，經過SVD降噪后，原始振動信號中與軸承故障無關的沖擊成分已經得到了大幅衰減。然后，對降噪后信號進行基于階次跟蹤的包絡解調，得到降噪后角域信號的包絡波形如圖10所示。最后，進一步處理得到的包絡階次譜如圖11所示，譜圖中清晰可見18.09階次及其諧波，與軸承內圈故障特征階次18.088吻合。

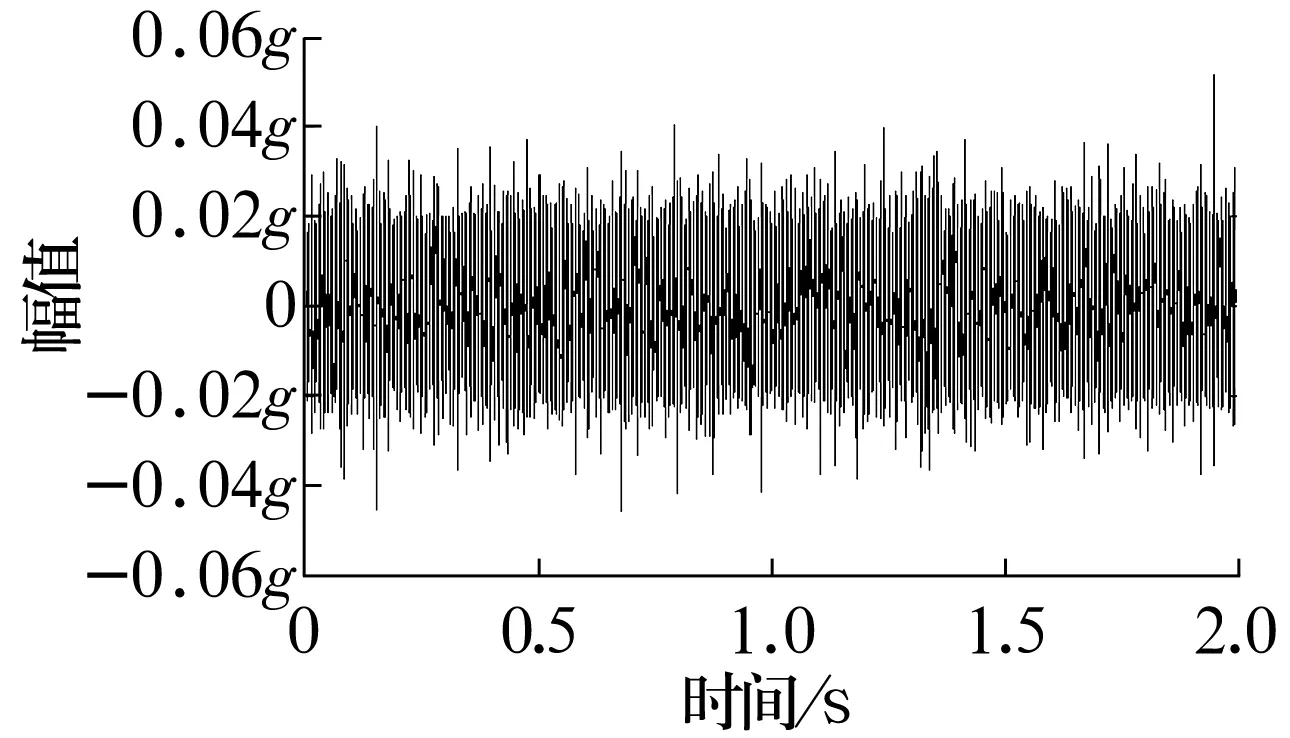
圖9 SVD降噪后的振動波形Fig.9 Vibration waveform after SVD denoising

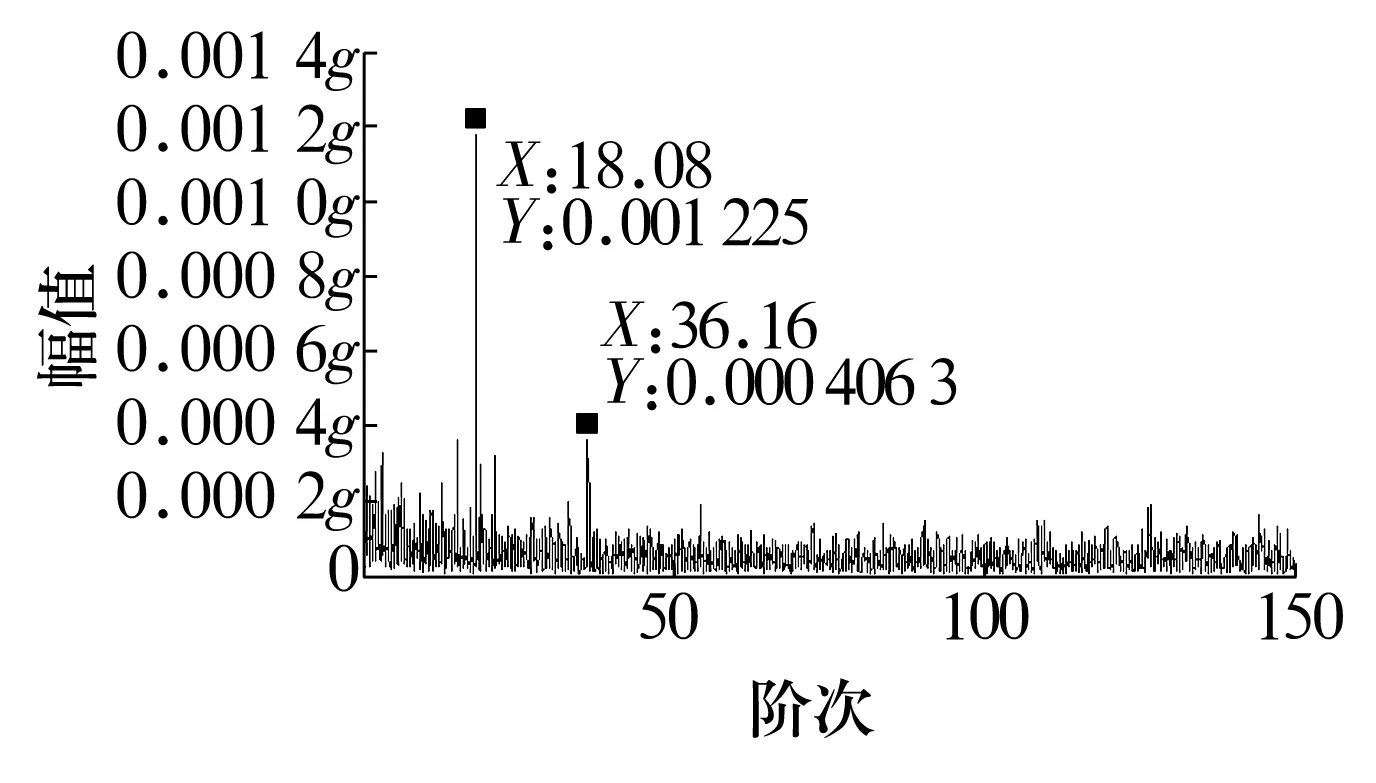
圖11 降噪后信號得到的包絡階次譜Fig.11 Envelope order spectrum obtained by denoised signal

為對比OTEO與SVD相結合方法的優勢及合理性，選取不同算法對圖7信號進行分析，結果如圖12和圖13所示。對比分析可知：單獨進行OTEO或SVD處理的效果均不佳，特征頻率完全被噪聲湮沒，無法提取出軸承內圈故障特征，說明OTEO與SVD相結合對于變轉速工況下軸承故障的識別十分有效。

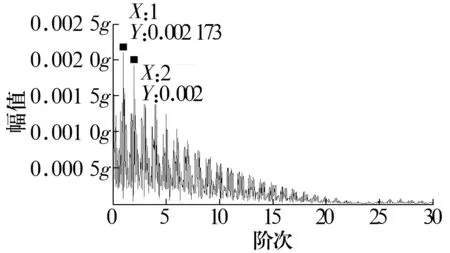
圖12 基于階次跟蹤和小波降噪的Hilbert包絡階次譜Fig.12 Hilbert envelope order spectrum based on order tracking and wavelet denoising

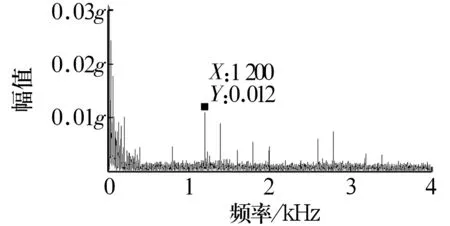
圖13 基于SVD降噪的EO包絡階次譜Fig.13 EO envelope order spectrum based on SVD denoising

5 結束語

針對實際應用中滾動軸承故障信號強干擾導致的信噪比低及變工況下故障特征提取中的頻譜模糊問題，選取SVD進行降噪處理，突出沖擊特征，然后采用OTEO克服變工況引起的頻率模糊問題，獲得可用于軸承故障識別的包絡階次頻譜，并成功提取出變工況運行滾動軸承的微弱故障。

該方法雖然在研究時考慮了工程化應用的因素，但仍缺乏企業現場數據的進一步驗證，下一步會采集更多數據用于該方法的實際驗證，以最終服務于工程問題。