巧用數形結合法破解絕對值函數的最值

浙江省寧波市第四中學 (315016) 蔣亞軍 魏定波

這是2017年浙江高考數學第17題，涉及絕對值函數的最值問題歷來受到競賽、自主招生、高考命題者的青睞，它的解法離不開分類討論，這種通法明顯比較繁瑣，本文從另一角度——“數形結合”法破解這類問題.

1 構建主元函數的圖像

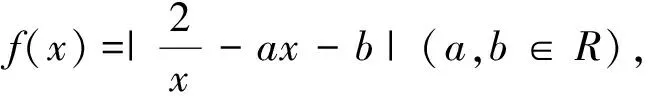
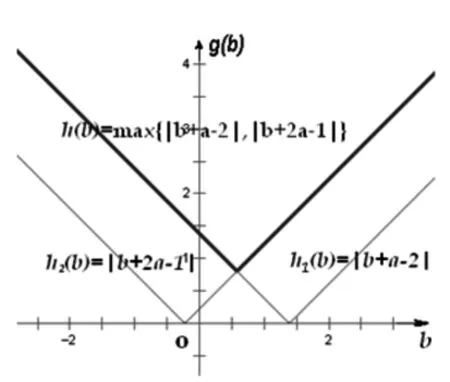
圖1

解析:所求問題等價于求函數y=f(x)在[1，2]上的最大值，由于a>0，f(x)max=max{f(1)，f(2)}=max

{|a+b-2|，|2a+b-

1|}(如圖1)，記g(b)=max{|a+b-2|，|2a+b-1|},依題意得g(b)≥m.

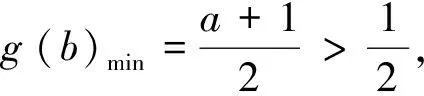
例2 (2015年高考(湖北卷)文科第17題)a為實數，函數f(x)=|x2-ax|在區(qū)間[0,1]上的最大值記為g(a).當a= 時，g(a)的值最小.

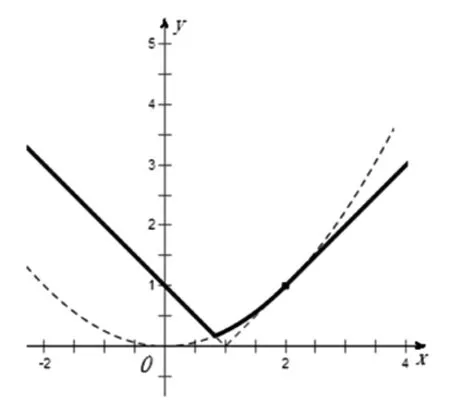
圖2

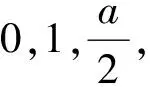
評注：對于數學中的多元參數問題，若按常規(guī)思路確定主元，可能導致問題復雜化，此時，若能針對題目的結構特征，改變思考的角度，選擇其參變量為主元，另辟蹊徑，往往可使問題化難為易，結合相關的思想方法，迅速獲解.

2.發(fā)揮圖形的直觀功能

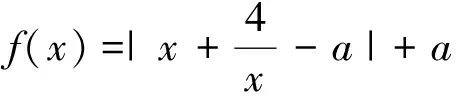
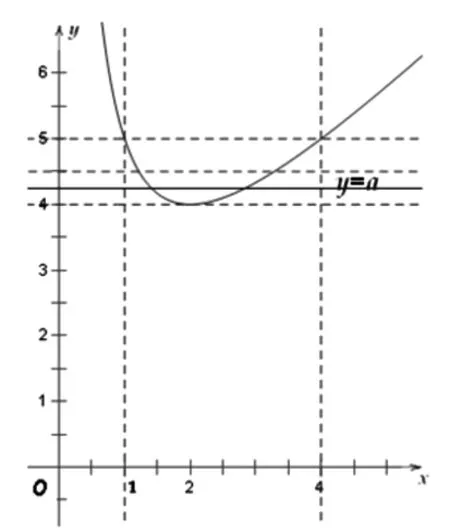
圖3

解析:考慮到f(x)=

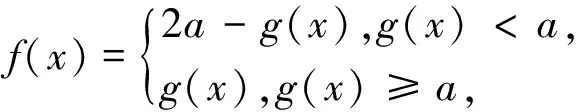
例4 (2011北約自主招生試題)求|x-1|+

|2x-1|+|3x-1|+…+|2011x-1|的最小值.

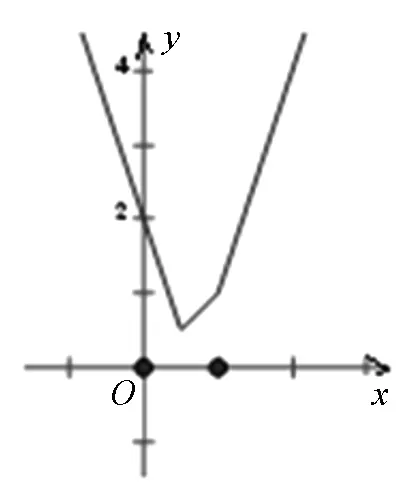
圖4-1

解析:設f(x)=|x-1|+|2x-1|+|3x-1|+…+

圖4-2

由于函數y=x+

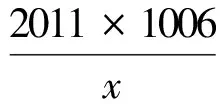
評注：2003年頒發(fā)的《普通高中數學課程標準(實驗)》中明確提出“高中階段的數學教學應加強幾何直觀教學，重視幾何圖形在數學學習中的作用，鼓勵學生借助直觀來思考”.運用幾何直觀來思考，解決最值函數的性質問題，省去了繁瑣的參數討論和復雜的計算過程，顯得更加直觀與簡單.

3.借助函數的逼近模型

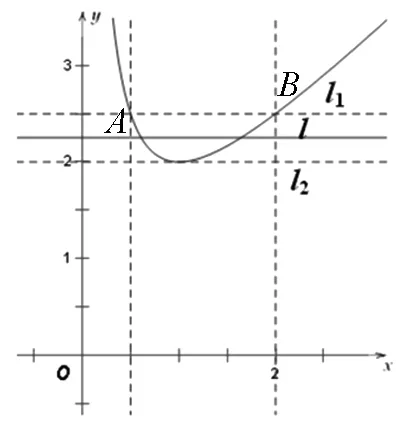
圖5

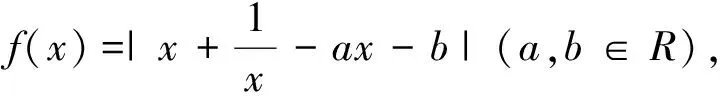
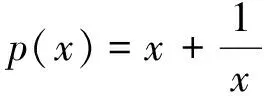
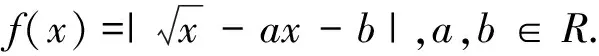
圖6

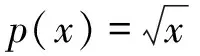
評注：上述問題的實質是俄羅斯數學家切比雪夫的最佳函數逼近問題，雖然超出了目前教學大綱，但是我們借助熟悉的“線性回歸”的思想，通過直觀圖形容易找出p(x)的最佳一次逼近q(x)=ax+b來.這樣一來，一個多參數的最值函數問題達到有效的、簡單的解決.

4.運用線性規(guī)劃的方法

圖7

例7 (2015年浙江省高考數學(理)科第18題)已知函數f(x)=x2+ax+b(a,b∈R)，記M(a,b)是|f(x)|在區(qū)間[-1,1]的最大值.

(Ⅰ)證明：當|a|≥2時，M(a,b)≥2；

(Ⅱ)當a，b滿足M(a,b)≤2時，求|a|+|b|的最大值.

解析:對于(Ⅰ)可以用構建主元函數的圖像的方法解決.

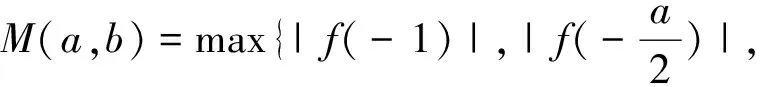
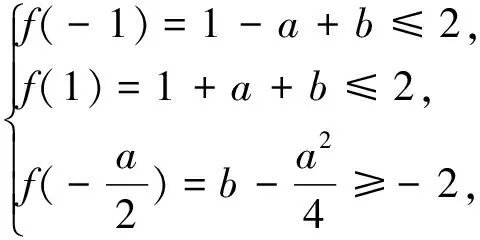
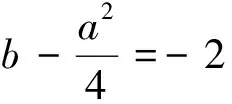
評注：解決二次函數中多個參數的綜合性問題，借助線性規(guī)劃的原理，運用數形結合的思想方法是不錯的選擇，它能避免一些復雜的不等式轉換，改變學生的思維定勢.