基于稀疏重構的混疊脈沖序列的周期估計

許成維，陶建武

空軍航空大學 航空作戰勤務學院，長春 130022

隨著社會信息化的快速發展，周期估計廣泛應用于電子偵察中脈沖重復間隔估計、節拍和節奏估計、神經學中峰值區間估計、呼吸率周期檢測、蛋白質編碼和脈沖星周期估計等各個軍民應用領域。尤其在電子戰領域的應用更為顯著，多用于電子干擾與反干擾的脈沖重復間隔(PRI)估計[1-7]。PRI是現代電子戰環境下雷達脈沖信號分選與識別的一個至關重要的參數。近年來，隨著電子戰技術的發展，電磁環境越發復雜、脈沖高度密集且相互交錯，影響了現代電子偵察技術的精確識別，這對于現代電子偵察提出了新的挑戰。當雷達發射脈沖信號時，為了防止對方輕易偵察到雷達發射的脈沖信號的重復間隔，往往會在發射脈沖時，加入人為干擾和抖動，導致了脈沖重復間隔的不確定性。由于接收設備自身原因和外界環境干擾因素，往往造成某些脈沖重復間隔上的脈沖缺失，導致測量脈沖串的不完整，使得測量脈沖串的周期性遭到破壞。尤其是在復雜電磁環境中，測量脈沖串通常是由多個具有不同周期的脈沖串混合疊加而成。這些因素都不利于信號周期的提取。

針對不完整脈沖串的周期估計，許多學者進行了大量的研究，如Fogel和Gavish[8]使用最大似然(ML)算法對帶有缺失和抖動的數據進行周期估計。Sadler和Casey[9]基于修正的歐式算法對最大公約數進行計算。Sidiropoulos等[10]在此基礎上，進一步發展了不完整脈沖串數據的周期估計方法。Clarkson[11]對最大似然估計做了改進，并驗證了兩種估計方法在周期估計上的性能。Ye等[12-13]指出了改進的Fogel周期圖估計算法的性能是由空間網格的間隔決定，并從理論推導出合理的網格搜索間隔。McKilliam和Clarkson[14]通過使用Chirp z-變換和快速傅里葉變換，使其周期圖估計算法的計算復雜性減少到O(NlgN)。雖然這些算法在周期估計的精確度和減小計算復雜性方面做出了很大的改進，同時對于低信噪比和高缺失率的信號具有較好的性能。但是對于由多個具有不同周期的脈沖串混合疊加的脈沖序列，這些方法不能得到真實的周期估計。因此，限制了這些方法在復雜電磁環境中的應用。面對這些挑戰，需要我們提出全新的、可以應對各種復雜電磁環境的脈沖序列的周期估計方法。

近年來，隨著壓縮感知的提出與發展，其應用一直是關注熱點。基于Farey序列理論，Vaidyanathan和Pal[15]構造了一種能夠提取出信號隱藏周期的過完備字典。Tenneti和Vaidyana-than[16]將此字典用于心電圖、蛋白質編碼等真實信號的隱藏周期提取。但是，該字典是基于離散傅里葉變換(DFT)矩陣進行構造的，對于周期信號的表示不能形成一個完美的稀疏表示。基于Ramanujan結構字典(RD)理論，Vaidyanathan[17-18]提出了一種提取信號隱藏周期的方法。但是，在應用于帶有人為抖動的、不完整的混疊脈沖序列的周期估計時，該方法不能達到較好的提取效果。因此，針對由多個具有不同周期的脈沖串混疊而成的脈沖序列，本文提出了一種基于稀疏重構的隱藏子周期估計新方法。從理論上探討混疊脈沖序列的稀疏表示模型、稀疏字典的設計及隱藏子周期估計方法。通過仿真實驗驗證了此估計方法的可行性和有效性。

1 數據模型

假設周期脈沖信號的脈沖寬度遠小于脈沖的周期。因此，可以將周期脈沖信號看成具有單位幅值的周期脈沖序列，從而形成周期脈沖信號的點過程模型。本文考慮如下周期脈沖信號的點過程模型：一個周期脈沖信號為T0k+θ0(k∈Z)是連續的整數，T0為周期，θ0為初相位。對其進行N次觀測，其表達式為

tn=T0sn+θ0+ωnn=1,2,…,N

(1)

式中:ω1,ω2,…,ωN為隨機抖動(或稱為脈沖滑動誤差)；s1,s2,…,sN為不連續且未知的整數，由于外界環境干擾，會有部分脈沖未觀測到。這造成了接收到的脈沖信號不是連續和完整的，即s1,s2,…,sN是不連續的整數。圖1給出了從完整的周期脈沖信號到形成不完整且帶有脈沖滑動誤差的單脈沖序列的示意圖。

假設有M個具有不同周期的周期脈沖信號同時到達接收裝置，因此，整個脈沖序列是M個不完整且帶有脈沖滑動誤差的脈沖串混合而成，其表達式為

(2)

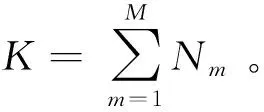
圖2給出了從兩個完整的脈沖周期信號到形成不完整且帶有脈沖滑動誤差的混疊脈沖序列的示意圖。圖2中，假設第1個脈沖序列的周期T1=15，第2個脈沖序列的周期T2=18。混合后，整個脈沖序列的周期為2個子脈沖序列周期的最小公倍數。本文所感興趣的是從整個脈沖序列中估計子脈沖序列的周期Tm。

2 結構字典矩陣設計

2.1 Farey結構字典矩陣

給定一個整數P，考慮所有不可約的有理數k/q,其中：整數q∈{1,2,…,P}，k為小于等于q、且與q互質的整數，即gcd(k,q)=1(1≤k≤q)。gcd(·)=1表示為兩個數的最大公約數為1，即它們是互質的。表1列出了在周期P=6時，有理數k/q的所有數值。將k/q的所有數值按從小到大的順序進行排列，得到一個有理數序列FP，即Farey序列。

表1 周期P=6時，有理數k/q的數值Table 1 Period P=6, rational values k/q

(3)

Vq=[v(q,k1)v(q,k2) …v(q,kφ(q))]

(4)

這里gcd(q,ki)=1和1≤ki≤q，Wq=e-j2π/q。進一步，定義一個P×Φ(P)維Farey序列字典矩陣為

(5)

例如，當P為6時，6×12維Farey序列結構字典矩陣為

(6)

利用Farey序列結構的字典矩陣，能夠將具有不同周期的混疊脈沖序列進行稀疏化表示，然后通過一定的稀疏恢復算法，獲得混疊脈沖序列的不同子周期。但是，字典矩陣維數的大小是影響稀疏恢復算法復雜性的關鍵因素，隨著P的增大，Φ(P)將急速增大，字典矩陣的維數增大。所以我們應設計一個合適的插值尺度來減少字典矩陣的維數。下面我們將Farey序列結構字典矩陣簡稱為Farey結構字典(FD)。

2.2 Ramanujan結構字典矩陣

Ramanujan 結構字典是由印度數學家Ramanujan提出的[19]，Vaidyanathan進一步發展了Ramanujan 結構矩陣， 其形式為[17-18]

(7)

其中:當0≤n≤q-1時，構成了周期序列cq(n)的主值區間。例如當q∈{1,2,…,6}時，則在主值區間，cq(n)的數值為

c1(n)={1},c2(n)={1,-1},c3(n)={2,-1,-1},c4(n)={2,0,-2,0},c5(n)={4,-1,-1,-1,-1},c6(n)={2,1,-1,-2,-1,1} 定義一個q×1矢量:

cq=[cq(0)cq(1) …cq(q-1)]T

它是由周期序列cq(n)主值區間的數值構成的。進一步，定義一個q×φ(q)矩陣：

(8)

如果序列的最大周期為Pmax，構造一個L×Φ(Pmax)維字典矩陣為

(9)

3 混疊脈沖序列的子周期估計

假設有M個具有不同周期的周期脈沖信號同時到達接收裝置，對接收裝置的測量值進行采樣，得到的采樣序列可表示為

(10)

式中：tk由式(2)給出。根據采樣定理，采樣間隔為

(11)

本文采用的均勻采樣是一種簡單而有效的方法，如果不考慮計算復雜性，盡可能使用較小的采樣間隔。當所有tk為整數，且min(tk-tk-1)≥2 (k=2,…,K)時，取Δt=1,在這種情況下，n=1,2,…,tK。將采樣序列y(n)寫成矢量形式，即Y=[y(1)y(2) …y(tK)]T。利用采樣序列和Ramanujan結構字典和Farey結構字典矩陣，采取稀疏重構方法估計混疊脈沖序列的子周期。

考慮下列稀疏優化問題：

(12)

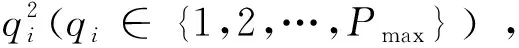
本文采用了聯合l2,0混合范數(JLZA)算法[20-22]求解稀疏優化問題，如式(12)所示。相比于文獻[16]提出的求解方法，JLZA算法對周期抖動和數據缺失的魯棒性更強。因為Ramanujan結構字典針對各個周期都有φ(q)列，因此，X的最優稀疏解X*是一個塊矢量，即最優稀疏解中，對應于每個子周期的φ(q)個連續元素構成一個塊矢量。利用式(13)計算最優稀疏解中的各個塊矢量的總系數G(P)：

(13)

當混疊脈沖序列含有某個隱含子周期時，最優稀疏解中對應于這個子周期的總系數G(P)將出現較大數值。

4 仿真實驗

4.1 不含有隱含子周期的單周期脈沖序列

假設一個不含有隱含子周期的單周期脈沖序列，如圖1所示。常數T=15，采樣間隔Δt=1，采樣序列的長度為400，幅值為1的脈沖個數為26。在沒有脈沖滑動誤差和脈沖缺失的情況下，圖3給出了3種方法的各個周期總系數G(P)隨周期P的變化情況。

從圖3(a)看出，在周期為15時，G(P)有明顯峰值，這說明JLZA-RD方法能夠正確估計出單周期脈沖序列的周期。從圖3(b)看出，在周期為1、3和5時，G(P)有最大的峰值。但在周期為15時，其峰值相對較小。這說明很難從G(P)的大小來判斷這個脈沖序列的周期。因此，2NCE-RD方法失效。從圖3(c)看出，在周期為1、3、5和15時，G(P)有相等的峰值，因此，與2NCE-RD方法個脈沖序列的周期。在脈沖缺失個數一定時，圖4給出了4種方法的成功概率隨滑動誤差變化曲線。在滑動誤差一定時，圖5給出了4種方法的成功概率隨脈沖缺失個數變化曲線。估計成功的概率定義為運行100次Monte Carlo實驗，正確估計出脈沖序列周期的次數除以100得到的數值。從圖4看出，JLZA-RD方法的估計性能最好。當參數δ≤0.15時，JLZA-RD方法的成功概率為1。這說明JLZA-RD方法的抗噪能力強。在脈沖缺失個數較少時，JLZA-FD方法的估計性能很好。這說明JLZA-FD方法的抗噪能力較強。2NCE-RD方法的估計性能最差，其成功概率小于0.2。其原因是G(P)不僅在周期為15處出現峰值，而且在周期為15的除數處也出現虛假峰值，且在大多數情況下，其虛假峰值高度大于在周期為15處的峰值。對于PDMax方法，滑動誤差較大時的成功概率大于滑動誤差較小時的成功概率，其原因是滑動誤差的增大，使得在周期為1、3和5處的峰值高度降低，其峰值高度小于在周期為15處的峰值高度。因此，其成功概率增加。從圖5看出，JLZA-RD方法的估計性能最好。在參數δ=0.1時，其成功概率不隨著脈沖缺失個數增加而減少，始終為1。這說明JLZA-RD方法的抗脈沖缺失個數能力較強。在脈沖缺失個數較少時，JLZA-FD方法的估計性能很好，但是，當脈沖缺失個數較多時，JLZA-FD方法的估計性能急劇下降,這說明JLZA-FD方法的抗脈沖缺失能力差。2NCE-RD方法的估計性能最差，其成功概率小于0.2。其原因如上所述。對于PDMax方法，其成功概率隨著脈沖缺失個數增加而減少，但是，減少的程度不大。這說明PDMax方法有一定的抗脈沖缺失能力。

4.2 隱含子周期的混疊脈沖序列

假設一個具有隱含子周期的混疊脈沖序列，如圖2所示。一個脈沖序列的周期T=15，初相θ0=1；另一個脈沖序列的周期T=18，初相θ0=1。采樣間隔Δt=1，采樣序列的長度為400，幅值為1的脈沖個數為48。在沒有脈沖滑動誤差和脈沖缺失的情況下，圖6給出了3種方法的各個周期總系數G(P)隨周期P的變化情況。

從圖6(a)看出，G(P)有兩個明顯的峰值，分別位于周期為15和18處。這說明JLZA-RD方法能夠正確估計出混疊脈沖序列的兩個隱含子周期。從圖6(b)看出，G(P)有多個峰值，其兩個最大峰值分別位于周期為1和3處，而在周期為15和18處，其峰值較小。根據G(P)取得最大值處的周期是估計周期的判斷原則，2NCE-RD方法不能正確估計出混疊脈沖序列的兩個隱含子周期。因此，2NCE-RD方法失效。從圖6(c)看出，PDMax方法與2NCE-RD方法相似，它也沒有正確估計出混疊脈沖序列的兩個隱含子周期。因此，PDMax方法失效。

在脈沖缺失個數一定時，圖7給出了4種方法的成功概率隨滑動誤差變化曲線。在滑動誤差一定時，圖8給出了4種方法的成功概率隨脈沖缺失個數變化曲線。

從圖7看出，JLZA-RD方法的估計性能較好。在滑動誤差較小時，JLZA-RD方法具有較高的成功概率。這說明JLZA-RD方法有一定的抗噪能力。在沒有脈沖缺失時，JLZA-FD方法的估計性能很好。這說明JLZA-FD方法的抗噪能力較強。對于2NCE-RD和PDMax方法，其成功概率接近于0。這說明這兩方法完全失效。其原因是G(P)具有虛假峰值，且虛假峰值的高度較大。從圖8看出，JLZA-RD方法的估計性能較好。在滑動誤差較小時，其成功概率ξ≤0.35時，始終為1。這說明JLZA-RD方法的抗脈沖缺失能力較強。JLZA-FD方法受脈沖缺失個數的影響較大。當脈沖缺失個數增加時，JLZA-FD方法的估計成功概率急劇下降。這說明JLZA-FD方法的抗脈沖缺失能力差。對于2NCE-RD方法和PDMax方法，其成功概率接近于0。這說明這兩方法完全失效。

當改變混疊脈沖序列的初相時，即一個脈沖序列的周期T=15，初相θ0=5；另一個脈沖序列的周期T=18，初相θ0=6，而其他條件不變。在沒有脈沖滑動誤差和脈沖缺失的情況下，圖9給出了3種方法的各個周期總系數G(P)隨周期P變化情況。與圖6比較，圖9(a)沒有變化，而對于圖9(b)，峰值的位置和幅度都有較大變化，對于圖9(c)，峰值的幅度有較大變化。這說明初相的改變對JLZA-RD方法沒有影響，而2NCE-RD和PDMax方法對初相的改變是敏感的。因此，不同的初相，2NCE-RD和PDMax方法的估計性能可能會變化。

為了進一步驗證初相變化對方法性能的影響。假設初相為均勻分布的隨機變量，而其他條件與圖9相同。在此條件下，對具有隨機初相的混疊脈沖序列進行100次周期估計實驗，圖10給出成功估計出序列周期的概率曲線。從圖10看出，在滑動誤差和脈沖缺失都為零的情況下，JLZA-RD方法對初相的隨機變化不敏感，其成功概率始終為1；而2NCE-RD和PDMax方法受初相改變的影響敏感，其成功概率始終為0。與圖7和圖8對比，在存在滑動誤差和脈沖缺失的情況下，JLZA-RD方法的成功概率變化較小。這說明了本文方法在各種情況下，對初相變化都具有較強的魯棒性。

通過上述實驗，可以得到如下結果：

1) 基于結構字典的稀疏重構方法具有較好的性能。JLZA-RD方法具有較強抗噪能力和抗脈沖缺失能力，并且不受初相的改變影響。JLZA-FD方法具有較強抗噪能力，但是，抗脈沖缺失能力較差。其原因是稀疏重構方法使用了聯合l2,0混合范數來進行優化，即確保未知矢量的非零元素的個數為最少。因此，通過稀疏優化迭代，不斷減小具有較小能量的峰值幅度，使其趨于零；同時不斷增大具有較大能量的峰值幅度，使其趨于最大。最終在脈沖序列的周期處，得到了幅度最大的峰值。

2) 2NCE-RD方法具有較差的性能，尤其是在具有隱含子周期的混疊脈沖序列的情況。其原因是2NCE-RD方法使用了l2范數來進行優化，即確保未知矢量的每個元素平方之和為最少。因此，相對于聯合l2,0混合范數優化，l2范數優化會使非零元素的個數增加。最終在多個周期處，出現幅度不等的峰值。這會給正確識別脈沖序列的周期帶來很大困難。另外，2NCE-RD方法對混和脈沖序列初相的改變是敏感的。

3) PDMax方法具有較差的性能，尤其是在具有隱含子周期的混疊脈沖序列的情況。其原因是PDMax方法使用了脈沖序列的功率譜來估計序列的周期。因此，與l2范數類似，會在多個周期處，出現幅度不等的功率譜峰值。這會給正確識別脈沖序列的周期帶來很大困難。

4.3 數據長度對脈沖序列估計性能的影響

在這個實驗中，對于單周期脈沖序列，我們給出了能夠正確估計出脈沖序列周期所需要滿足的最小序列長度。這里，我們將脈沖序列周期分解成素數的乘積。圖11給出了當脈沖序列周期P為素數(周期從2到60)時，序列長度隨周期P的變化。在圖11中，由星號標記的數據表示沒有脈沖滑動誤差的情況下，估計出脈沖序列周期所需要滿足的最小序列長度；而由正方形標記的數據表示有脈沖滑動誤差δ=0.1的情況下，估計出脈沖序列周期所需要滿足的最小序列長度。兩條曲線是由指數函數擬合序列長度數據所得到的結果。從圖11看出，周期的大小是影響所需最小序列長度的關鍵因素。周期增大，所需最小序列長度近似按指數曲線增大。

當脈沖序列周期P為兩個以上素數(素數1除外)乘積時，在沒有脈沖滑動誤差的情況下，序列長度隨周期P(周期從4到40)的變化如表2～表4所示。從表2看出，所需最小序列長度不僅與周期的大小有關，還與分解的兩個素數中的最大素數有關。最大素數的數值增大，所需最小序列長度相應增加。例如，周期為14(素數分解為2×7)和15(素數分解為3×5)時，雖然14比15小，但是由14分解的兩個素數中的最大素數是7，而由15分解的兩個素數中的最大素數是5，因而，估計周期14所需最小序列長度大于估計周期15所需最小序列長度。

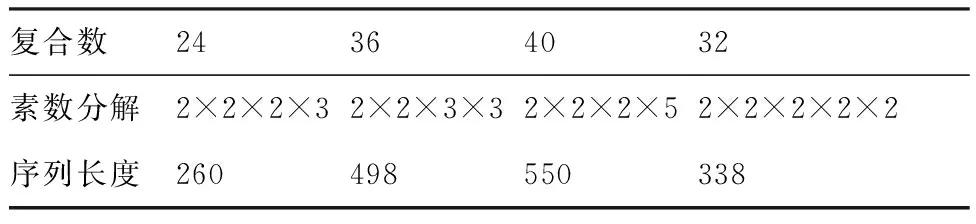
從表3和4看出，所需最小序列長度還與分解的素數多少有關。分解素數的個數增多，所需最小序列長度相應增加。例如，在周期為36(素數分解為2×2×3×3)時，分解素數的個數是4，因而，估計周期36所需最小序列長度大于估計周期37、38(素數分解為2×19)、39(素數分解為3×13)所需最小序列長度，其中，周期37分解素數的個數是1，而周期38和39分解素數的個數是2。總之，對于單周期脈沖序列，能夠正確估計出脈沖序列周期所需要滿足的最小序列長度不但與脈沖序列周期的大小有關、還與分解素數的個數和其中的最大素數有關。

表2 序列長度隨周期P的變化(P分解為2個素數乘積)

表3 序列長度隨周期P的變化(P分解為3個素數乘積)Table 3 Variation of sequence length with period P (P is decomposed into prouct of three prime numbers)

表4序列長度隨周期P的變化(P分解為4個以上素數乘積)

Table4VariationofsequencelengthwithperiodP(Pcanbedecomposedintoproductoffourormoreprimenumbers)

復合數24364032素數分解2×2×2×32×2×3×32×2×2×52×2×2×2×2序列長度260498550338

5 結 論

1) 仿真實驗表明，基于結構字典的稀疏重構方法具有較好的性能。JLZA-RD方法具有較強抗噪能力和抗脈沖缺失能力，并且不受初相的改變影響。JLZA-FD方法具有較強抗噪能力，但是，抗脈沖缺失能力較差。2NCE-RD和PDMax方法具有較差的性能，尤其是在具有隱含子周期的混疊脈沖序列的情況。

2) 對于單周期脈沖序列，能夠正確估計出脈沖序列周期所需要滿足的最小序列長度不但與脈沖序列周期的大小有關、還與分解素數的個數和其中的最大素數有關。