一種面向航空集群的集中控制式網絡部署方法

呂娜，劉創，陳柯帆，曹芳波

空軍工程大學 信息與導航學院，西安 710077

近年來，隨著飛行器的更新換代，尤其是無人機的迅速發展，航空平臺的信息化、智能化水平不斷提升，推動了空中作戰模式的改變。為了使多個航空作戰平臺實現綜合化、體系化作戰，研究人員將生物集群的理念應用到航空作戰領域，提出航空集群的概念[1-3]。航空集群作戰為了實現多平臺間戰術協同和平臺能力優勢互補，需要依托機載網絡將大規模空中平臺靈活組網。

當前，以航空數據鏈和航空自組網為代表的機載網絡一直遵循著傳統分布式網絡架構的設計思路[4]。通過不斷升級網絡設備的各種軟硬件雖然能夠一定程度上保證網絡性能的提升，但是這種“打補丁”的方式效率很低，不僅使得網絡變得更加臃腫，也使得網絡管理與配置過程復雜且僵化，導致網絡服務能力擴展和升級變得十分困難，難以保障未來航空集群各成員間的靈巧作戰協同。

軟件定義網絡(Software Defined Networking，SDN)的出現為傳統分布式網絡的發展帶來了全新的研究思路，它使網絡控制平面與數據平面分離，通過邏輯集中控制的方式對網絡設備進行統一管理[5]。與傳統網絡相比，SDN具有更高的靈活性、更強的可編程性和更大的開放性。SDN在小型數據網絡中已經得到了廣泛應用，但是隨著SDN在大中型網絡中的應用，控制平面的健壯性和可擴展性面臨著重要挑戰[6]。

從網絡演進的角度看，SDN的靈活性、開放性、可編程性等優勢正好可以彌補現有機載網絡在航空集群作戰應用背景下存在的弊端，具有較好的應用前景。目前相關的研究已經展開，如文獻[7-8]均指出SDN網絡范式應用于機載網絡能夠帶來眾多優勢。文獻[9]在總結航空集群作戰特點和SDN設計思想的基礎上提出了軟件定義航空集群機載戰術網絡，并對其基本網絡架構進行闡述。但是這些研究的內容主要聚焦在概念和基本網絡架構描述，缺乏深入的理論建模分析。在航空集群環境下由于節點的高移動性和航空信道的不可靠性等因素使得控制器難以像地面網絡一樣與網絡節點有效可靠地交互信息，這對控制平面的健壯性和可擴展性提出了更大挑戰。而如何在航空集群作戰環境下，構造符合網絡需求的控制平面，解決大規模及動態網絡下控制平面可擴展性差的問題，是實現SDN范式在機載網絡中實際應用的重要前提。

為了解決單一控制器的性能瓶頸和單點失連問題，提高網絡的可擴展性，多控制器的架構被普遍采用。現有的多控制器架構主要分為3類[10]：扁平式體系結構如Onix、Ethane,垂直架構如Kandoo、Logical xBar等，和以Orion為代表的混合層次式體系結構。在多控制器的架構下，研究人員發現控制器的部署位置和數量會直接影響到控制層面的性能，近年來針對控制器部署問題(Controller Placement Problem，CPP)的研究逐漸成為研究熱點[11-12]。控制器部署是實現控制平面構建的基礎和前提。在網絡拓撲動態變化和網絡連通性不穩定的機載網絡中，控制器的位置不僅會影響到新流建立的時延，而且會直接影響到網絡的配置和管理效率和網絡的可靠性等方面。因此，在以航空集群為背景的集中控制式網絡中對控制器部署問題進行研究，提出合適的優化模型和求解方法，對于提升網絡性能具有重要意義。

前期對于CPP的研究背景主要集中在地面有線SDN，研究內容主要集中在性能尺度以及搜索算法兩個方面。文獻[13]首次提出控制器放置問題，指出CPP問題求解的關鍵點是控制器數量和控制器在網絡拓撲中的位置，同時作者闡述了不同控制器部署方案對網絡時延性能的影響。在此基礎上，文獻[14]提出了可靠性優化的控制器部署問題，并針對這一問題提出了相應的貪心算法和模擬退火算法進行求解。除時延和可靠性外，控制器的負載均衡及網絡彈性和容錯性也是求解CPP問題考慮的重要性能尺度。文獻[15]針對控制器的負載均衡問題，首次提出容量限制的控制器部署問題(Capacitated Controller Placement Problem, CCPP),并針對這一問題提出基于K-center的啟發式算法，求解滿足控制器容量限制的最小控制器數量。上述研究主要針對扁平式的控制器架構，沒有考慮層次型控制器部署的需求。文獻[16]針對層次型多中心SDN控制器部署問題，通過減少圖劃分的域間割邊數以降低SDN跨域流數量來提高流表構建效率。文獻[17]在綜述已有研究的基礎上，也指出未來對CPP的研究應從實用性角度出發設計求解方法，以便指導同類或相似的網絡場景中CPP的求解。

可以看出，現有CPP的研究主要面向固定拓撲的地面有線網絡，沒有考慮到動態拓撲下無線網絡的部署需求。由于機載網絡與地面有線網絡的巨大差異，如在控制器架構上，受高動態的網絡拓撲和頻繁的鏈路中斷影響，以往CPP研究基于的扁平式多控制器架構就難以適用于航空集群場景，同時針對地面網絡所設計的性能尺度和搜索算法也不能符合航空集群的優化需要。因此在航空集群背景下對CPP研究，應該在總結網絡場景需求特點的基礎上，結合控制器架構設計符合實際應用的性能尺度選取和求解算法。而目前相關研究由于缺乏這些考慮，在實際應用時很難有較好的指導意義。

針對上述問題，本文從航空集群控制平面的可擴展性出發，研究了混合層次式的多控制器架構及其部署問題。在提出適合航空集群的控制器架構基礎上，將傳統的多控制器直接部署轉化為子域劃分和域內部署兩個步驟。提出了基于節點密度排序(Node Density Ranking, NDR)的子域劃分算法。考慮到控制器的負載均衡，對NDR擴展提出了容量限制下(Capacitated Node Density Ranking, CNDR)的子域劃分算法。考慮到網絡的動態特性，從網絡整體性能角度選取控制鏈路的平均時延和平均失連率作為優化目標，在子域劃分的基礎上提出了改進的Pareto模擬退火(Improved Pareto Simulated Annealing，IPSA)對多目標優化問題求解。

1 模型設計

1.1 場景及控制器架構描述

本文討論是基于如圖1(a)所示的集群作戰應用場景，該場景中存在預警機、戰斗機、偵察機、無人機等多種類型的作戰平臺，它們依據作戰階段的不同任務動態組織。與傳統SDN應用場景不同，在航空集群環境中，網絡節點的移動性使得控制器與控制域內傳輸節點的穩定互聯變得十分困難；高對抗的戰場環境使得控制器存在較高的失連風險；無線鏈路的不可靠性使得扁平式控制器架構難以實現多個控制器之間及時有效的信息共享；基于上述考慮，為實現對集群平臺的有效網絡管控和提高網絡的可擴展性，航空集群環境中應采用混合層次式控制器架構實現對網絡的邏輯集中控制。

文獻[18]提出了一種用于大規模網絡的混合層次式控制器架構，本文在此基礎上，考慮到航空集群的特殊應用場景，做出以下設定。航空集群環境下的混合層次式控制器架構如圖1(b)所示，考慮到網絡規模，本文將控制平面分為兩層。頂層由全局控制器(Globe Controller，GC)組成，GC負責跨區域流量計算和轉發。由于航空集群平臺能力之間存在較大差異，GC應該部署于預警機、指通機等生存能力和綜合信息處理較強的平臺之上，GC之間通過定向天線對各自負責區域內收集到的網絡視圖信息進行交互，進而形成掌握全局網絡信息的主控制平面。主控制平面從全域戰場的視角對整個航空集群網絡進行管控，具有最高的控制優先級。

底層由本地控制器(Local Controller，LC)組成，其僅具有自身控制域內的本地網絡視圖信息，向上與GC共同維護全局網絡視圖，向下負責管理本地設備和本地流量的轉發。LC是根據網絡節點規模和分布、網絡流量等情況按需部署在集群平臺上的。由于其與平臺內的網絡設備共用底層物理硬件資源，可以根據網絡變化情況在相應平臺上開啟或者關閉本地控制器，實現對本地網絡設備的彈性管控。動態變化的本地控制器形成本地控制器資源池，與全局控制器共同形成控制邏輯集中的航空集群網絡的控制平面。本文只對該控制器架構進行簡要概念描述，重點研究該架構下本地控制器的部署問題。

1.2 問題建模

在上述混合層次式控制器架構下，本文研究內容為在已知網絡節點和全局控制器數量和位置的情況下，求解滿足網絡管理的性能需求時的LC控制器數量和部署位置。

考慮到實際部署SDN時，傳統分布式網絡和SDN是共存的，控制器部署是按照覆蓋網(overlay)方式，即在原有網絡基礎上部署一個邏輯控制層面[19]。針對部署場景做以下假設：

1) 網絡中每個節點代表一個交換機，本文統稱為傳輸節點，控制器為co-located部署方式，即控制器和交換機可以部署于網絡同一節點，此種情況下認為兩者的傳輸時延為0。

2) 除GC之間單獨配置定向鏈路共享網絡視圖信息，其他控制路徑均為帶內(in-band)方式，即控制信息和數據信息走相同路徑，不單獨部署控制信道。

3) 網絡中每個交換機在同一時間只能由唯一的LC控制，每個LC也只能由唯一的GC控制。

為形式化地描述本地控制器LC部署問題，將網絡建模成一個無向圖G=(V,E,S,M)，其中V={v1,v2,…,vq}代表拓撲中網絡節點集合，q為拓撲中節點數量;E={(vs,vt|vs,vt∈V)表示網絡節點之間鏈路的集合；M={m1,m2,…mm}表示全局控制器集合;S={s1,s2,…,sk}表示本地控制器集合，其中S?V且M?V；定義傳輸節點與LC的連接矩陣G=[xvs]|V|*|S|和LC與GC之間的連接矩陣H=[ysm]|S|*|M|，xvisj=1時，說明節點vi屬于控制器sj的控制域下，反之則為0。相應的ysimj=1時，表示LC節點si屬于GC節點mj的控制域下。

2 子域劃分算法的設計

航空集群執行任務過程中，網絡拓撲結構相對保持穩定。作戰任務改變，網絡拓撲結構發生變化。在航空集群環境下，應當由掌握全網視圖信息的全局控制器根據網絡環境變化運行LC部署算法得到部署結果，并將LC啟動信息在全網廣播。根據該信息，網絡中的相應節點啟動控制器模塊成為LC。

從上述部署流程中可以看出，LC資源池的方式使得控制器部署可以靈活適應網絡拓撲結構的變化，有利于對本地網絡設備的彈性管控。但這也給CPP算法的設計提出了較為苛刻的要求。首先集群構型的改變具有時間限制；其次航空集群規模通常較大，平臺數量一般能達到上百架以上。對于CPP的求解是NP難問題，當網絡規模達到上百個時，根據使用算法不同，求解時間最大能夠達到幾個小時。為防止在大規模動態網絡環境下求解CPP時間過長導致LC部署無法完成，本文算法的設計重點是在簡化算法時間復雜度并保證解的精確性基礎上，求解出較優的LC部署方案。

2.1 基于節點密度排序的子域劃分算法

為了區分節點在網絡中的位置，本節首先引入兩個定義，鄰居密度ρi和最短距離δi。

定義1節點的鄰居密度ρi為

(1)

式中:Dij為節點si和節點sj之間的實際距離;Dc為距離閾值，函數Γ被定義為

(2)

從式(1)中可以看出節點的鄰居密度僅與Dc的取值有關。由于不同拓撲構型的網絡節點鄰居密差異較大。在相同拓撲下，閾值越大，計算越復雜，而閾值越小，難以有效區分不同節點的鄰居密度。因此，本文設置Dc為

Dc=0.3max(Dij)

(3)

定義2節點最短距離δi為

(4)

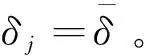
根據定義一個具有較大ρi和δi值的節點，更有可能成為子域的頂點。對于在一定區域內隨機分布的節點，為了找到子域的頂點，首先根據定義計算每個節點的鄰居密度ρ和連接距離δ。然后分別根據ρ值和δ值對節點排序，將排序號相加得到節點的總排序號，按照總排序號值和LC數量k得到區域頂點集Scon。最后按照到區域頂點距離最短的原則將網絡節點劃分為k個子域。算法1給出了NDR的描述細節。

算法1基于密度排序的子域劃分算法NDR

輸入：節點位置，LC數量k

輸出：子域集N

1) for eachs∈Sdo

2) 根據式(1)和式(4)分別計算每個節點的pi和δi3) end for

4) 將節點集V分別按照p值和δ值降序排列得到V1和V2

5) 記錄每個節點的對應排列序號i和j

6) 將每個節點的p值排列序號i和δ值排列序號j相加，得到總排列序號

7) 將節點集V按照總排列序號值升序排列得到Vcon

8) 取前k個點形成區域頂點基Scon

9) for eachs∈Sdo

10) 計算每個節點到區域頂點的距離

11) end for

12) 按照距離區域頂點距離最短的原則，將網絡分成k個子域N={N1,N2,…,Nk}

2.2 控制器容量限制下的子域劃分算法

上述對子域的劃分沒有考慮控制器容量的限制，無法得到符合網絡需求的控制器數量，實現對CCPP問題的求解。對于邏輯集中控制的機載網絡，控制器的數量對網絡性能有著重要影響。因為在集群作戰過程中，平臺多以編隊云的形式執行作戰任務。屬于同一編隊云的作戰單元空間跨度較小、信息交互需求較高。將同屬于一個編隊云的節點放到同一本地控制域下，可以有效減少對GC的訪問降低流表建立的開銷和時延，因此子域數量應該盡可能小。但是子域數量對應于需要部署的LC數量k，當k值過小時，本地控制器負載將會失衡，這將嚴重影響控制器的控制效能。綜合以上考慮，本文將考慮控制器容量的LC部署問題定義為滿足網絡負載性能要求的最少LC數量。

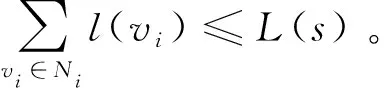
算法2給出了容量限制的子域劃分算法CNDR。首先，根據算法1得到區域頂點集Scon。然后，根據Scon中節點排序情況，依次選取序號靠前的節點作為子域頂點，形成多個子域，計算每個子域的LC負載情況。最后逐漸增加子域規模直到求出所有子域都滿足負載均衡要求時的最小k值。

為了評估多個子域之間的負載情況，文獻[20]定義了負載均衡指數B，其表示子域間交換機提交的平均信息量之和的最大差值。需要說明的是，由于航空集群的特殊環境，部署結果發送到相應節點時間周期較長。而請求信息量是動態變化的，算法2使用的節點平均信息量只能通過預測或統計來大致判斷子域的負載情況。

(5)

算法2容量限制的子域劃分算法CNDR

輸入：節點位置，網絡負載均衡指標

輸出：子域N,LC數量k

1) 首先根據算法1的1)～7)行，得到按照總排列序號值排序的Vcon

2) fori=1:n

3) 取Vcon中前i個節點作為頂點

4) 按照距離區域頂點距離最短的原則，將網絡分成i個子域

5) 根據式(5)計算每個區域內的負載情況

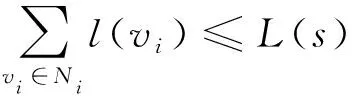
7) 返回此時的i值和分域情況N

8) break

9) end if

10) end for

為了說明CNDR-DPA算法的計算過程，在400 km×300 km的區域隨機部署36個節點，對節點編號，節點分布如圖2(a)所示。設置節點的通信半徑R=80 km。根據算法1的1)～7)行，得到按照總排列序號值排序的Vcon，表1為Vcon總排序號靠前的部分節點排序情況。假設每個節點的流表策略配置需求l(v)相同，本地控制器的額定負載L(s)=t×l(v)。當t為9，并取至Vcon的第5個節點時，計算所有子域的負載情況,均滿足額定負載要求，此時網絡將以節點{18,25,1,28,20}為子域頂點，按照最短距離優先原則將節點分成5個子域，得到節點分區結果如圖2(b)所示，分別用5種不同形狀的點表示。

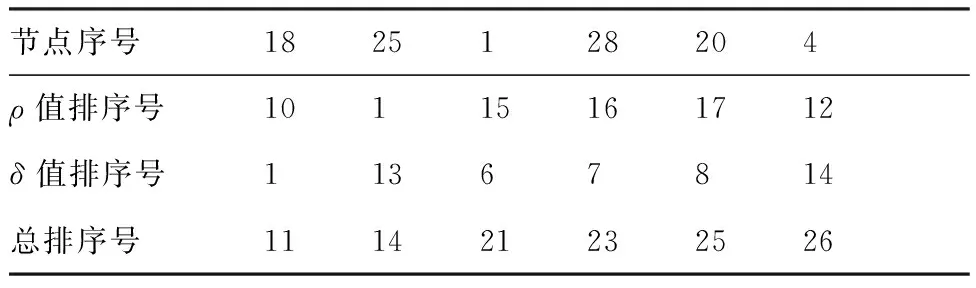
節點序號1825128204ρ值排序號10115161712δ值排序號 11367814總排序號 111421232526

3 域內LC的部署優化

3.1 優化性能指標

將網絡節點劃分成多個子域后，需要根據網絡性能尺度和搜索算法找到控制器在每個子域中的適當位置。由于航空平臺的動態移動性和網絡狀態的時變性，本文在LC部署過程中從網絡的整體性能角度出發，考慮到混合層次式的控制器架構設計了以下兩種性能尺度。

1) 控制路徑平均傳播時延

網絡的控制路徑平均傳播時延反映的是網絡中控制路徑傳播時延的整體情況。在大尺度分布的航空集群應用場景下，網絡的發送時延、排隊時延和處理時延相對于傳播時延小很多，傳播時延為整個通信時延主要的影響因素。控制路徑的平均傳輸時延包括交換機與LC間平均傳播時延和LC與GC之間的平均傳播時延，它嚴重影響控制平面對網絡事件的響應速度和管控效率。本文將控制路徑的平均傳播時延定義為傳輸節點到LC間平均傳輸時延和LC與GC之間的平均傳輸時延之和：

(6)

式中：d(vi,sj)為傳輸節點vi及LC節點sj之間的最短路徑時延集合；d(si,mj)為LC節點sj與GC節點mj之間的最短路徑時延集合。

2) 控制路徑平均失連率

在邏輯集中控制式的網絡中管理和控制網絡的命令是通過控制路徑傳輸的，控制路徑的可靠性直接關系到整個網絡的可靠性。由于航空鏈路質量的不穩定性，控制鏈路出現容易出現中斷現象，同時在戰場環境下傳輸節點具有較高的失連概率。文獻[21]已經做出了關于網絡可靠性的研究工作。在這里，為了對網絡控制路徑的可靠性進行評估，本文定義控制路徑的平均失連率，它是指控制路徑失去連接概率的均值，包括交換機與LC失連概率和LC與GC失連概率。設控制鏈路中斷率為d1和傳輸節點失效率為p1，則控制路徑平均失連率為

(7)

式中：l∈(V,S)為傳輸節點到LC節點的控制路徑集合；l∈(S,M)為LC節點到GC節點的控制路徑集合。

3.2 域內LC部署算法

本文對每個子域內LC的部署位置求解過程中以最小化控制路徑平均傳播時延和控制路徑平均失連率為目標，這是一個多目標優化問題。由于多個目標之間存在沖突，因此多目標優化最終得到多個Pareto解。

以往對于CPP的求解主要考慮的是域內的性能尺度，因此在子域劃分完成之后，可以通過逐個子域進行遍歷搜索的方式求解到控制器在每個子域內合適的位置。而本文設定的優化目標考慮的是控制鏈路的整體性能，LC的位置是相互影響優化目標的，因此必須從整個網絡的角度來求解出控制器在每個子域內的部署位置，但這也顯著增加了計算的復雜度。

對于多目標優化問題求解的時間復雜度和精確性取決于所選取的算法，為了在有限時間內搜索出精確結果，本文采用Pareto模擬退火(Pareto Simulated Annealing，PSA)算法。PSA算法是基于蒙特卡羅迭代求解法的一種多目標啟發式隨機搜索算法，實現簡單、計算效率高，通過合理的參數設置可以在計算時間和解的精確性之間權衡，具有較高的靈活性。

根據以上分析，利用算法1或算法2對網絡節點分區后，需要在每個子域內部署一個控制器。為了滿足LC部署問題需求和求解方便，本文對PSA算法進行改進(IPSA)，算法3中描述了求解流程，有如下關鍵步驟：

1) 種群個體初始化。算法中的種群個體是由k個元素構成的向量X，k為LC節點的數量。PSA算法通常會采用完全隨機的初始種群，這種方法雖然能夠保持較好的種群多樣性，但是容易生成適應度差的個體，不利于算法收斂。本文設置初始種群為子域頂點集Sopt，這樣鄰居密度更高的節點成為初始種群可以有效節省PSA算法的初始運行時間，提高精度。

2) 目標函數權重。合理的目標函數權重可以保證產生的解具有良好的多樣性。PSA算法在每迭代過程中用一系列產生樣本的解來控制目標函數權重的大小。如果x第一次迭代或者沒有一個最靠近樣本x的非劣解x′，則設置權重為隨機值且滿足?λi≥0，∑λi=1；否則，則設置每個目標函數fi的權重為

(8)

式中：α>1。

4) 接受概率P。PSA算法的接受概率與權值大小有關，通過對權值大小的控制可以增加或降低某個目標的接受概率。PSA是以概率P接受新解。

(9)

算法3基于改進PSA的域內LC部署

輸入：G=(V,E)，Sopt，k，m，初始溫度T0，降溫系數p

輸出：Pareto解集M，LC部署位置

1) 初始化目標權重λi,T=T0

2) 初始解X=Sopt，計算所有目標函數值并加入Pareto解集M中

3) whileT>1 do

4) 產生鄰域解Y，并計算其所有目標函數值

5) 比較新產生的鄰域解Y與Pareto解集M中的每個解并更新Pareto解集M

6) 根據式(8)和式(9)分別計算權重λi和接受概率P

7) 如果Y未進入Pareto解集M，以概率P接受Y，如果新解被接受，則令其為X，如果新解未被接受，則保留當前解

8) if 完成m次迭代 then

9)T=Tp

10) end if

11) end while

4 實驗結果及分析

4.1 仿真環境及參數說明

對于實驗的相關環境和參數作出如下說明：

1) 在一臺主頻為3 GHZ、內存為8 GB的PC上，基于MATLAB環境下對本文算法進行仿真。

2) 由于目前尚不存在實際應用的具體參數作為參考，為簡化實驗過程作出以下假設：所有本地控制器都有相同的負載容量、處理能力等；所有的傳輸節點向控制器提交的請求信息量相同，設l(vi)=1；單個節點和鏈路的故障率為區間[0,0.04]和[0,0.08]之間的隨機數；值得說明的是，這種參數設置僅影響具體的計算值，并不影響對算法正確性的驗證，實際應用時可根據全局控制器掌握的具體參數信息進行計算。IPSA算法的具體參數在4.4節實驗中根據節點數量進行設置。

3) 本文算法并不考慮GC的數量和位置對網絡性能的影響。因此規定在實驗過程中，節點數量小于100時，GC數量為1。節點數量大于100時，GC數量為2。GC的部署位置為隨機指定的節點。

4) 考慮到航空集群中各作戰單元依據作戰動態組織，在網絡拓撲上表現為隨機動態變化。為了體現這一特點，實驗中使用的拓撲是在給定區域內隨機生成多個節點，利用Dijkstra算法得到任意兩點間的最短路徑方式獲得的。實驗中設置網絡節點分布區域的大小為700 km×600 km，節點的通信半徑R為120 km。

由于在相同節點數量下，不同網絡拓撲結構的網絡性能具有一定差異。為了驗證本文算法在不同網絡節點規模下的有效性和適用性，實驗過程中將相同節點數量作為一種實驗條件，為了排除節點位置變化對算法驗證的影響，對比的性能指標是相同實驗條件下得到不同網絡拓撲結構性能優化結果的均值。具體實驗次數和網絡拓撲數量在各小節實驗中說明。

為了綜合評估本文算法的有效性，在實驗過程中，選取3種解決大規模SDN控制器部署問題的算法作為對比，3種算法的主要描述如表2所示。第1種是基于社團發現的控制器部署算法。第2種是以K-means代表的聚類問題求解算法。第3種是將啟發式算法引入到CPP問題求解。前兩種算法為降低時間復雜度，都采取了子域劃分域內部署控制器的設計思路。

表2 對比算法描述Table 2 Description of comparison algorithms

4.2 NDR劃分算法分析

為了驗證NDR對網絡節點的子域劃分情況，分別在節點規模為60、100、140的航空集群網絡環境中，每個節點數量下隨機生成10個拓撲，比較不同節點規模下的負載均衡指標隨控制器數量變化情況，并以LPA和K-means算法作為對比。對于LPA和K-means算法，因為子域劃分過程帶有隨機性，因此實驗結果采用多次仿真取平均值的方法。

實驗結果如圖3所示，子域劃分LPA和K-means算法的子域規模不可控，負載均衡指數波動較大，且遠遠高于NDR算法，因此極易出現控制器負載不均衡的情況。3種子域劃分算法在計算過程中都沒有對控制器容量進行限制，LPA算法利用節點標號在網絡中任意傳播直至收斂來進行子域劃分，K-means算法是通過迭代計算將節點按照最小時延劃分為K個類別，而NDR算法在劃分子域過程中主要考慮周圍節點的密度和網絡節點的分布情況，因此可以獲得更優的負載均衡指數。需要說明的是，本節僅比較了不同算法的子域負載均衡指數，實際上控制器的負載狀況不僅與子域規模有關，也與控制器在子域中的位置相關。實驗也表明，利用NDR算法將網絡劃分多個子域，可以有效限制子域規模之間的差距，對實現控制器的均衡具有良好效果。

4.3 CNDR劃分算法分析

為了驗證CNDR算法對于CCPP求解的有效性，本節在節點規模從50～200的區間里，隨機生成100個網絡拓撲，使用CDNR算法計算每個拓撲在具有相同控制器容量限制下所需的最小LC數量。本文使用文獻[15]提出的求解CCPP問題的K-center算法作為對比。K-center算法是一種基于啟發式的隨機搜索算法，通過迭代尋找滿足控制器負載均衡的K個中心，來求解出網絡所需的控制器部署數量和位置。實驗中，每個傳輸節點向LC提交的請求信息為[0.5,1.5]之間的隨機數，但所有傳輸節點向對應LC提交的請求信息總量為N，N為節點數量。實驗結果如圖4所示，x軸表示LC數量，y軸表示滿足控制器負載均衡的拓撲在所有拓撲中所占比例。

從圖4中可以看出，使用CNDR算法,當控制器個數超過10時，50%以上的拓撲能夠滿足控制器容量的要求;當控制器個數達到20時，所有的拓撲都可以滿足控制器容量的要求。而使用K-center算法，需要的控制器數量為15～26個。實驗結果表明，使用CNDR算法相比于K-center算法求解所需的控制器數量更少，求得CCPP問題解的質量更高。這是因為本質上K-center是一種啟發式搜索算法，主要思想是通過反復迭代找到滿足控制器容量限制的K個中心。在節點數量較多的情況下，K-center算法容易陷入局部最優解。而CNDR算法只需數學計算即可，不會陷入局部最優。

4.4 IPSA性能分析

為了評估IPSA算法的優化性能，本節設置場景中的節點個數為80，LC數量為k=6，在子域劃分基礎上，以控制路徑的平均傳播時延Tavg和平均故障率σavg作為目標函數，對LC部署進行優化。為了在求解精度和求解時間之間權衡，根據網絡節點規模，設置IPSA中迭代次數m=30，初始溫度T0=150，降溫系數p=0.90。實驗過程中使用窮舉算法(Brute Force，BF)對子域間所有解的組合進行遍歷搜索，尋找問題最優解，作為對比驗證IPSA算法在求解精度上的損失和計算時間上的優勢。

首先重復實驗100次，驗證IPSA算法的穩定性，記錄Tavg和σavg的取值情況。圖5為100次實驗平均傳播時延和平均失連率的取值情況變化，圖中橫線為使用BF算法得到的最優值。Tavg在[0.807,0.887]內波動，波動幅度為±2.36%；σavg波動區間為[0.122,0.135]，波動幅度為±1.36%。

表3給出了BF、IPSA和PSA 3種算法的平均性能比較。3種算法都是在利用NDR算法進行子域劃分的基礎上進行優化求解的。從表中結果可以看出，通過改進的PSA算法——IPSA算法具有更高的穩定性，且更接近最優解。

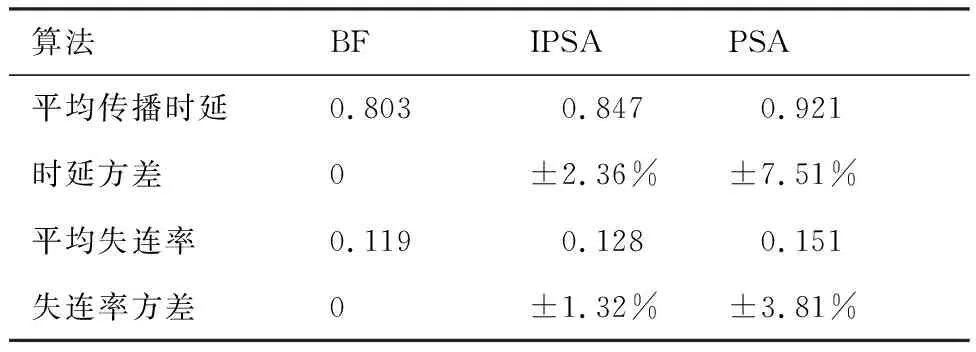
表3 100次獨立實驗平均性能比較

圖6為采用IPSA、POCO、PSA和BF算法獲得的Pareto解最優前沿。從圖中可以看出，控制路徑平均失連率和平均傳輸時延成反比。相比于PSA算法和POCO算法，IPSA算法得到了較為平滑且均勻的Pareto面，且解更接近BF算法得到的結果。注意圖中給出的Pareto解為滿足優化目標的一組權衡解，實際的控制器部署過程中應該根據網絡性能需求，從Pareto解集中選擇合適的方案。

4.5 本文算法的優化性能分析

本節利用LPA、K-means、POCO和本文所提的NDR和IPSA算法(以下用NDR-IPSA統一表示)對LC部署優化性能進行驗證。節點規模為100，對比算法的迭代次數均為200次，IPSA算法參數中m=20，初始溫度T0=100，降溫系數p=0.95。首先，驗證LC數量對網絡性能的影響。圖7和圖8分別給出了在不同LC數量下控制路徑的平均傳播時延Tavg和平均失連率σavg，實驗數據為各算法重復計算50次的平均值。

從圖7和圖8均可以看出，隨著LC個數的增加，平均傳播時延Tavg和平均失連率σavg均逐漸降低。其中，Tavg平均降低了46.7%，σavg平均減少了24.8%。因此，在航空集群集中控制式的網絡中增加本地控制器的數量可以有效減少控制鏈路的平均時延和平均失連率。對比其他3種算法，POCO優化性能更好，這是因為當劃分子域過多時域內節點數量將變少，這直接限制了算法的優化能力。而與本文算法在子域劃分中僅考慮節點鄰居密度不同的是，K-means是根據預先定義的優化目標進行子域劃分的，更具靈活性，在子域數量較多的情況下優化性能也好。

圖9為4種算法的計算時間隨LC數量變化情況，可知LPA和K-means算法隨著LC數量的增加，計算用時平穩增長，增長幅度較小。而POCO隨著LC數量的增加，計算用時顯著增長，增長幅度較大。與這3種算法不同，本文算法的計算用時快速減小。這是因為隨著LC數量增加，子域數量也在增加，IPSA算法的搜索空間逐漸減小。LPA和K-means是基于迭代的子域劃分方法，因此在網絡規模一定的情況下，子域數量增多反而增加了時間復雜度，而NDR-IPSA算法只需要一次計算就可以實現網絡區域的劃分。

圖10給出了在不同節點數量下計算時間的對比情況。隨著節點數量的增加，4種算法的計算時間都在增加，其中POCO算法計算時間遠高于LPA、K-means和本文算法，在節點數量為120以上時POCO的平均計算時間是本文算法的6倍左右。可以看出，與使用啟發式算法的POCO表現不同的是，使用子域劃分域內部署控制器的方式可以顯著降低大規模SDN控制器部署的時間復雜度，但是結合圖7和圖8的仿真可以看出，這種方式也損失了解的精確度。對比可知，本文所提算法更適用于大規模網絡及動態拓撲環境下的控制器部署問題。

5 結 論

1) 針對航空集群的特殊環境，通過擴展控制層級和定義本地控制器資源池的方式，使得控制器部署可以靈活適應網絡拓撲的變化，增強了網絡的可擴展性。

2) 為了滿足本地控制器快速部署需求，針對航空集群環境下節點規模大、計算復雜度高的問題，提出了NDR和IPSA算法，通過仿真驗證了本文算法提升網絡性能的有效性和在大規模網絡及動態拓撲環境下的適用性。

3) 考慮到控制器的負載均衡，為了求解出網絡需要的控制器數量，對NDR擴展提出了CNDR，并通過仿真驗證了該算法對于解決CCPP問題的有效性。